判断两矩形是否相交

转自Avril，略有改动

---

 

Problem：

给定两个边与坐标轴平行的矩形，分别由左上角与右下角两点指定，判断两矩形是否相交。

---

 

Solution：

如下图所示，首先求出$P_1$与$P_3$点(即坐标值较小的两点）在$X$方向较大值与$Y$方向较大值构成的点，在下图中就是$P_3$，用红点(记为M点)表示。

然后求出$P_2$与$P_4$点(即坐标值较小的两点）在X方向较小值与Y方向较小值构成的点，在下图中就是$P_2$，用橙色点(记为N点)表示。

如果M点的X坐标和Y坐标值均比N点相应的X坐标和Y坐标值小，亦即M和N可以分别构成一个矩形的左上角点和右下角点，则两矩形相交；其余情况则不相交。

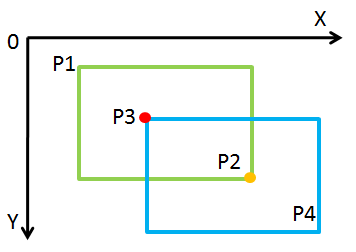
                                   图1

 

 

下图给出第二个示例，表明相交则矩形的某一个顶点位于另一矩形内部作为判断依据是错误的。

                            图2

 

图3给出了相互包含的情况：

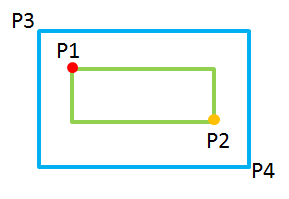
                            图3

下图给出了不相交时的示例，两矩形为上下关系，可见红点不在橙色点左上角，不能构成矩形，因此不相交。

                          图4

 

下面的例子同上，给出了两矩形为左右关系的情况。

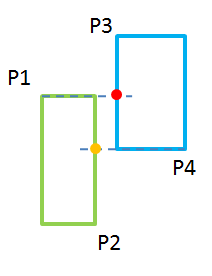
                 图5