【POJ 1269】Intersectiong Lines（两条直线关系）

思路：我们先判断这两条直线是否平行 若平行 再去判断是否重合 若不平行 算交点

具体实现：
对于平行 我们直接判断v1,v2的叉积（v1,v2是来表示L1,L2的向量）是否为0

对于重合 我们把l1上的端点p1代入l2 判断叉积

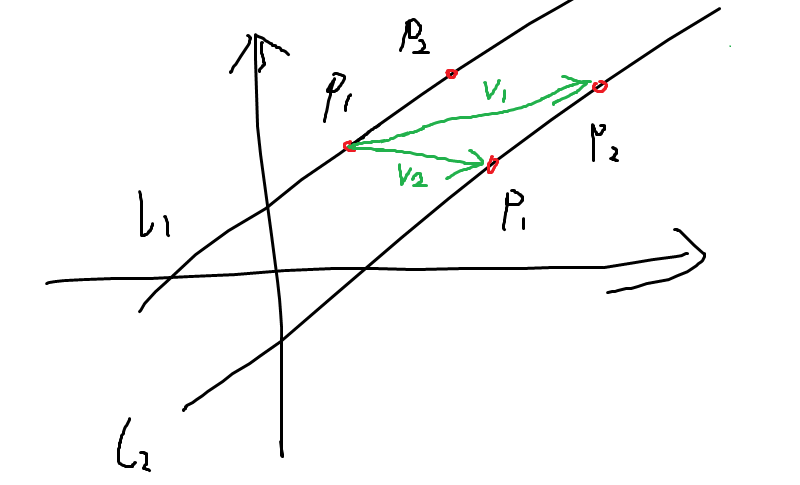
如图 只需判断v1,v2的叉积是否为0 ，可以画个重合的图自行理解

对于算交点 暴力用一次函数的方法解方程 不过除数有可能为0 需要特判垂直于x轴的线

附代码

#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cmath>
#define N 100005
#define eps 1e-8
using namespace std;
int n;
struct Point 
{
    double x,y;
    Point(){};
    Point(double x,double y):x(x),y(y){};
}p[N];
typedef Point Vector;
Vector operator +(Vector a,Vector b)
{
    return Vector(a.x+b.x,a.y+b.y);
}
Vector operator -(Vector a,Vector b)
{
    return Vector(a.x-b.x,a.y-b.y);
}
double Dot(Vector a,Vector b)
{
    return (a.x*b.x)+(a.y*b.y);
}
double Cross(Vector a,Vector b)
{
    return (a.x*b.y)-(a.y*b.x);
}
double Len(Vector a)
{
    return sqrt(Dot(a,a));
}
struct Line
{
    Point p1,p2;
    Line(){};
    Line(Point p1,Point p2):p1(p1),p2(p2){};
}l1,l2;
int main()
{
    cin>>n;
    puts("INTERSECTING LINES OUTPUT");
    while(n--)
    {
        cin>>l1.p1.x>>l1.p1.y>>l1.p2.x>>l1.p2.y;
        cin>>l2.p1.x>>l2.p1.y>>l2.p2.x>>l2.p2.y;
        Vector v1=l1.p1-l1.p2;
        Vector v2=l2.p1-l2.p2;
        if(fabs(Cross(v1,v2))<eps)//平行 
        {
            Vector v3=l1.p1-l2.p1;//把l2.p1代入直线1
            Vector v4=l1.p2-l2.p1; 
            if(fabs(Cross(v3,v4))<eps)    puts("LINE");    //重合 
            else puts("NONE");
        }
        else
        {
            double k1=0,k2=0,b1=0,b2=0;
            cout<<"POINT ";
            if(l1.p1.x-l1.p2.x==0)//垂直于x轴
            {
                k2=(l2.p1.y-l2.p2.y)/(l2.p1.x-l2.p2.x);
                b2=l2.p1.y-k2*l2.p1.x;
                printf("%.2f %.2f\n",l1.p1.x,k2*l1.p1.x+b2);
                continue;
            }
            if(l2.p1.x-l2.p2.x==0)
            {
                k1=(l1.p1.y-l1.p2.y)/(l1.p1.x-l1.p2.x);
                b1=l1.p1.y-k1*l1.p1.x;
                printf("%.2f %.2f\n",l2.p1.x,k1*l2.p1.x+b1);
                continue;
            }
            k1=(l1.p1.y-l1.p2.y)/(l1.p1.x-l1.p2.x);
            b1=l1.p1.y-k1*l1.p1.x;
            
            k2=(l2.p1.y-l2.p2.y)/(l2.p1.x-l2.p2.x);
            b2=l2.p1.y-k2*l2.p1.x;
            
            printf("%.2f %.2f\n",(b2-b1)/(k1-k2),(k1*b2-k2*b1)/(k1-k2));
        }
    }
    puts("END OF OUTPUT");
}