『格路径计数的一个简单结论』

\(\mathrm{Lemma}\ 1.\) 从\((0,0)\)到\((n,m)\)的矩形格路径条数为二项式系数\(\binom{n+m}{n}=\binom{n+m}{m}\).

证明：将两种移动的方案视为球染色分方案即可.

\(\mathrm{Corollary}\ 1.\) 从\((0,0)\)到\((n,n)\)不越过直线\(y=x\)的格路径条数为卡特兰数\(\mathrm{C}_n\).

证明：向右走对应数字进栈，向上走对应数字出栈，则路径条数对应序列出栈方案数，即为卡特兰数\(\mathrm{C}_n\).

\(\mathrm{Corollay}\ 2.\) 从\((0,0)\)到\((n,m)(n\geq m)\)不越过直线\(y=x\)的格路径条数为\(\binom{n+m}{m}-\binom{n+m}{m-1}\).

证明：

考虑补集转化，总路径条数为\(\binom{n+m}{m}\)，只需计算不合法路径条数，如图：

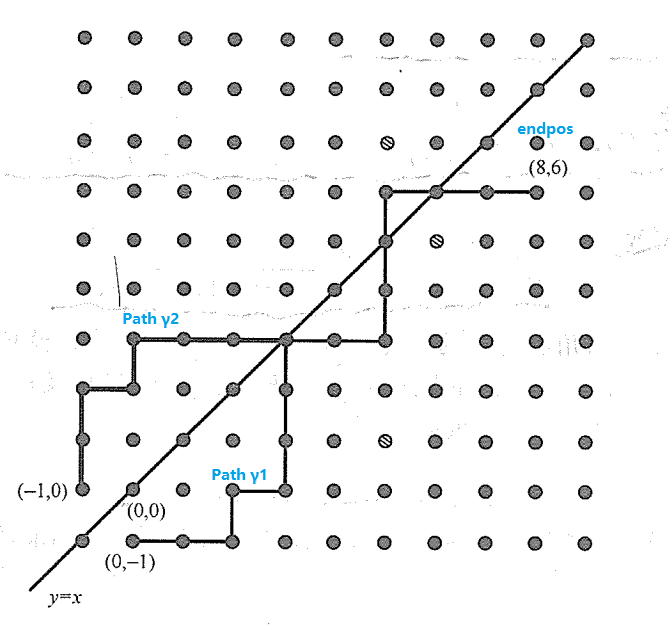
对于从\((0,0)\)到\(\mathrm{endpos}(n=8,m=7)\)的非法格路径，可以向下平移得到从\((0,-1)\)到\((n=8,m-1=6)\)的接触直线\(y=x\)的格路径，那么现在考察这样的路径有多少条.

显然，任何一条接触直线\(y=x\)的格路径都有一个最早接触点\((a,a)\)，不妨称\((0,-1)\)到\((a,a)\)的子路径为\(\mathrm{Path}\ \gamma_1\). 根据反射原理，所有\(\mathrm{Path}\ \gamma_1\)和以\((-1,0)\)为起点，\((a,a)\)为终点的路径\(\mathrm{Path}\ \gamma_2\)一一对应，由于从\((-1,0)\)到\((n,m-1)\)的路径必然经过\(y=x\)，那么总共的接触直线\(y=x\)的格路径条数就和\((-1,0)\)到\((n,m-1)\)的路径总数一一对应.

所以不合法的路径条数就是\(\binom{n-(-1)+m-1}{m-1}=\binom{n+m}{m-1}\)，那么结论得证.