『数据结构总结2:线段树』
Preface
由于内容较多,这篇博客可能会龟速更新,以总结各类线段树为主.
原理
线段树是一种用于维护序列区间信息的数据结构,针对序列\(a_{1\sim n}\),建立满足如下性质的满二叉树:
- 每个树上节点表示一个区间\([l,r]\),具有唯一根节点表示区间\([1,n]\)
- 对于每一个非叶子节点\([l,r]\),有且仅有两个儿子\([l,\mathrm{mid}]\)和\([\mathrm{mid}+1,r]\)
- 对于叶子节点\(p\),其表示的区间为单位区间\([x,x]\)
一般情况下,线段树的区间中点\(\mathrm{mid}\)取\(\lfloor\frac{l+r}{2} \rfloor\)以保证时间复杂度,特殊情况另外考虑.
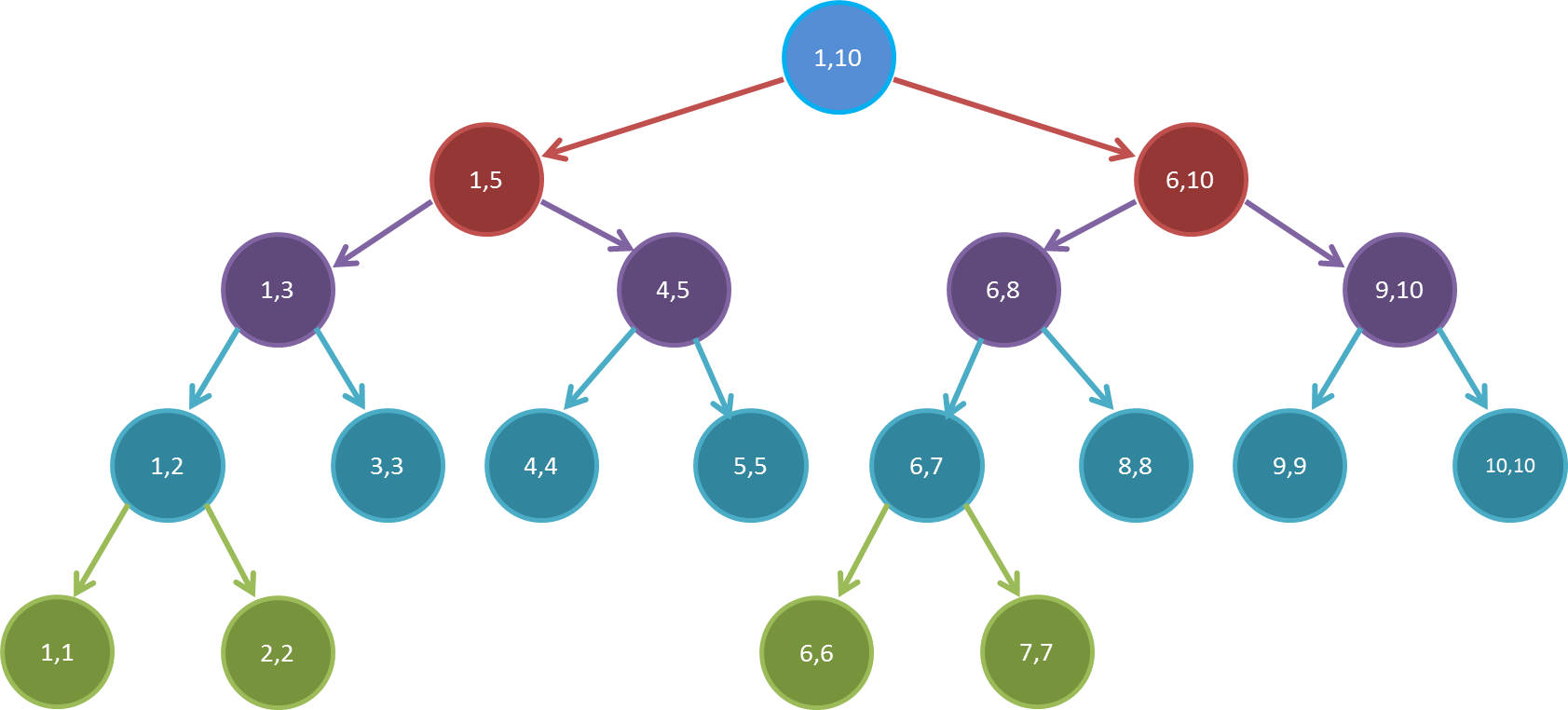
\(n=10\)情况下某一序列的线段树结构如图所示.
线段树用于解决广义的区间求和问题,定义如下:
给定序列\(a_{1\sim n}\)和元素集合\(\mathrm{S}\),满足\(\forall i\in[1,n]\ a_i\in \mathrm{S}\),定义加法运算符\(+:\mathrm{S}\times \mathrm{S}\rightarrow\mathrm{S}\),满足结合律,不必要满足交换律,每次询问一个区间的\(+\)和\(\sum_{i=l}^ra_i\).
对于序列\(a_{1\sim n}\),我们建立线段树,并在每一个节点\([l,r]\)处处理出区间\([l,r]\)的和:对于叶子节点\(p\),可以直接得到\(v_p=a_p\),对于非叶子节点\(p\),计算\(v_p=v_{\mathrm{lson}(p)}+v_{\mathrm{rson}(p)}\). 此预处理时间复杂度为\(O(n)\).
对于区间询问,可以证明任意区间\([l,r](1\leq l\leq r\leq n)\)在线段树上最多只对应\(\mathcal{O}(\log_2n)\)个节点区间的并,于是可以直接递归遍历树找到这些点,然后求和. 由于区间连续,且每一层最多访问两个节点,所以时间复杂度是\(\mathcal{O}(\log_2 n)\)的.
如果存在减法运算符\(-:\mathrm{S}\times \mathrm{S}\rightarrow \mathrm{S},a-b\overset{\mathrm{def}}{=}c\ \mathrm{s.\ t.}\ b + c=a\),则该问题可以使用前缀和\(\mathcal{O}(n)-\mathcal{O}(1)\)解决,但是线段树还支持单点修改.
针对一个点的元素修改,显然会影响到线段树上\(\log_2n\)个祖先的值,那么只需要直接更新这\(\log_2 n\)个祖先的值即可,时间复杂度\(\mathcal{O}(\log_2 n)\).
对于某个修改算符\(c\),如果在已知\(\sum_{i=l}^r a_i\)的情况下,可以\(\mathcal{O}(1)\)求出\(\sum_{i=l}^r c(a_i)\). 则针对算符\(c\),线段树还可以实现区间修改:我们在每个非叶子节点\(p\)上维护一个懒标记\(s_p\),表示\(p\)节点的值已经被正确的修改,但是\(p\)的儿子还未被修改. 对于一个操作\((l,r,c)\),遍历线段树上\([l,r]\)对应的\(\mathcal{O}(\log_2n)\)的节点,修改出它们正确的\(v_p\),并沿路更新它们的祖先即可. 同时,我们在这些节点上修改\(s_p\),表示修改操作对子节点暂时没有作用的影响.
那么在任何线段树操作中,假设我们访问到了\(p\)节点,我们需要先处理掉懒标记\(s_p\)才能访问其子节点\(\mathrm{lson}(p)\)和\(\mathrm{rson}(p)\),这样所有修改的正确性得以保证. 并且区间修改的时间复杂度为\(\mathcal{O}(\log_2 n)\).
实现
区间加法,区间求和的线段树参考代码如下,使用宏定义可以大大减小代码量.
struct Node { ll tag,sum; };
struct SegmentTree
{
Node ver[N<<2];
#define tag(p) ver[p].tag
#define sum(p) ver[p].sum
#define mid ( l + r >> 1 )
#define ls p << 1 , l , mid
#define rs p << 1 | 1 , mid + 1 , r
inline void Apply(int p,int l,int r,ll d) { sum(p) += (r-l+1) * d , tag(p) += d; }
inline void Spread(int p,int l,int r) { if ( tag(p) ) Apply(ls,tag(p)) , Apply(rs,tag(p)) , tag(p) = 0; }
inline void Update(int p) { sum(p) = sum(p<<1) + sum(p<<1|1); }
inline void Modify(int p,int l,int r,int ml,int mr,ll d)
{
if ( l > r || ml > mr || mr < l || ml > r ) return void();
return ( ml <= l && r <= mr ) ? Apply(p,l,r,d) :
( Spread(p,l,r) , Modify(ls,ml,mr,d) , Modify(rs,ml,mr,d) , Update(p) );
}
inline ll Query(int p,int l,int r,int ql,int qr)
{
if ( l > r || ql > qr || qr < l || ql > r ) return 0;
return ( ql <= l && r <= qr ) ? sum(p) :
( Spread(p,l,r) , Query(ls,ql,qr) + Query(rs,ql,qr) );
}
} T;
但是线段树可以实现的功能远不至于此,由于一般的题目中没有固定的模板,所以各种常见的其他线段树及其实现方式将在下一节讨论.
功能
区间加法/乘法,区间求和/求最值
基本操作,时间复杂度均为\(\mathcal{O}(\log_2 n)\).
区间加乘,区间求和
问题在于如何同时维护两种\(+/\times\)修改操作. 首先要维护两个懒标记是肯定的,剩下的问题就是所谓优先级,也就是我们到底是把一段区间的值记为\(aS+b\)还是\((S+b)\times a\). 显然第一种更好,因为乘法是对加法有分配律的,无论是再乘一个数还是再加一个数都可以很快地更改懒标记,而第二种对于加法标记就难以更改,因为括号外面有一个系数.
对于一般的问题,不妨从两个方面考虑:\(1.\) 如何快速得到一段区间修改后的答案. \(2.\) 如何下传标记更新儿子的信息. 而第二个方面就事关优先级一类的问题了.
值域二分
把线段树开成值域数组,我们同样可以实现查询第\(k\)大数的功能. 原理和树状数组是类似的:定义一个问题\((l,r,k)\)表示查询值域区间\([l,r]\)内第\(k\)大的数,只需考察\([l,\mathrm{mid}]\)内有多少个数,设为\(x\),若\(x\geq k\),则问题等价于\((l,\mathrm{mid},k)\),反之则等价于\((\mathrm{mid}+1,r,k-x)\),直接在线段树上递归下去即可. 由于查询一个线段树上区间的和的时间复杂度是\(\mathcal{O}(1)\),所以总时间复杂度就是\(\mathcal{O}(\log_2n)\).
inline int Select(int p,int l,int r,int k) { return l == r ? l : ( sum(p<<1) >= k ? Select(ls,k) : Select(rs,k-sum(p<<1)) ); }
动态开点
动态开点指的是一种优化线段树空间的技巧. 对于一般的线段树,其空间复杂度和\(n\)有关. 假如我们要开一棵值域线段树,那么空间复杂度就和值域有关了. 一种很方便的解决方法就是改用变量记录每一个线段树节点的左右儿子,如果遇到一个之前从未遍历过的儿子,那就给它一个新的标号即可,这样空间就优化到了\(\mathcal{O}(m\log_2n)\).
线段树优化建图
图论问题中有一类模型需要将一个点与一个编号连续的区间连边,并且原问题的解与只与图的连通性和边权有关,与边数无关,那么我们可以使用线段树来优化此类建图问题.
具体来说,我们显式建出序列\([1,n]\)的线段树,并将所有叶节点\([x,x]\)连向原图的点\(x\),无需维护任何区间信息. 对于一个连边操作\((x,l,r)\),只需在线段树上找到区间\([l,r]\)所对应的\(\mathcal{O}(\log_2n)\)个线段树区间,然后向这些点连边即可. 根据线段树的连通性,显然和原图是等价的.
根据线段树的性质,一次连边的时间复杂度降为\(\mathcal{O}(\log_2 n)\),总的空间复杂度为\(\mathcal{O}(n+m\log_2 n)\).
inline void Build(int p,int l,int r)
{
if ( l ^ r ) id[p] = ++tot; else return void( id[p] = l );
Build(ls) , Insert( id[p] , id[p<<1] );
Build(rs) , Insert( id[p] , id[p<<1|1] );
}
inline void Connect(int p,int l,int r,int cl,int cr,int x)
{
if ( l > r || cl > cr || cr < l || cl > r ) return void();
if ( cl <= l && r <= cr ) return Insert( x , id[p] );
Connect( ls , cl , cr , x ) , Connect( rs , cl , cr , x );
}
二维偏序
一般的值域数据结构可以支持在线一维偏序问题的查询,事实上我们可以通过数据结构的嵌套支持在线二维偏序问题的查询.
一般的在线二维偏序问题可以用树套树或者\(\mathrm{cdq}\)分治解决,但是树套树的码量和常数较大,\(\mathrm{cdq}\)分治不支持强制在线. 其实我们有一种很简单的解决方案:树状数组套线段树.
记\(\mathrm{Seg}(S)\)表示集合\(S\)中所有元素构成的值域线段树,我们只需令树状数组的元素表示线段树,即
那么一个二维偏序的查询就可以放到\(\log_2n\)棵线段树上,时间复杂度\(\mathcal{O}(\log^2 n)\),并且可以支持动态加点,时间复杂度相同.
这样做的空间复杂度是\(\mathcal{O}(n\log^2n)\),内部需要用动态开点的线段树,其缺点在于要求值域不能过大,如果值域过大,可以把外层树状数组换成另一颗值域线段树,这样时空复杂度均为\(\mathcal{O}(\log^2 \max \{a_i\})\).
主席树
主席树一般指的是线段树的可持久化,并时间轴放在下标上. 不过一般可持久化线段树的应用也基本是这样. 我们知道对一棵线段树进行单点修改只会涉及到修改\(\mathcal{O}(\log_2n)\)个节点,那么我们完全可以不在原节点上修改,把修改过的节点新建出来,实现可持久化. 这样空间复杂度变成了\(\mathcal{O}(n+m\log_2n)\),时间复杂度不变.
以查询区间第\(k\)大问题为例,主席树的代码其实很短:
struct Node { int ls,rs,sum; };
struct PresidentTree
{
Node ver[N*40]; int root[N],tot;
#define sum(p) ver[p].sum
#define ls(p) ver[p].ls
#define rs(p) ver[p].rs
#define mid ( l + r >> 1 )
#define Ls ls(q) , l , mid
#define Rs rs(q) , mid + 1 , r
inline void Update(int p) { sum(p) = sum(ls(p)) + sum(rs(p)); }
inline void Modify(int &p,int q,int l,int r,int x,int v) {
if ( p == 0 ) p = ++tot; ver[p] = ver[q]; if ( l == r ) return void( sum(p) += v );
return ( x <= mid ? Modify(ls(p)=0,Ls,x,v) : Modify(rs(p)=0,Rs,x,v) ) , Update(p);
}
inline int Query(int p,int q,int l,int r,int k) {
if ( l == r ) return l; int t = sum(ls(q)) - sum(ls(p));
return k <= t ? Query(ls(p),Ls,k) : Query(rs(p),Rs,k-t);
}
};
还有一类问题,可能需要支持区间修改的主席树,事实上,这类问题几乎可以被完美解决.
何出此言?首先大多数此类问题都使用了标记永久化的方法来解决,但是标记永久化具有较大的局限性,不是任何线段树能维护的信息都能用标记永久化的. 其次,一部分言论认为下传标记的主席树空间开销巨大,不宜在算法竞赛中使用,事实上并非如此,接下来我们介绍区间修改的可持久化线段树.
首先我们要理解可持久化的思想是只新建,不修改. 从时间复杂度角度考虑,为什么区间修改的线段树仍是\(\mathcal{O}(\log_2 n)\)的,因为它只修改\(/\)调用\(\mathcal{O}(\log_2 n)\)个节点,即使我们使用了懒标记的技巧.
对于区间修改上,我们不妨把下传标记也看做一种对节点的修改,那么只需要秉承只新建,不修改的思想即可. 具体来说,对于\(\mathrm{Apply}\)函数,我们返回修改过的节点编号,对于\(\mathrm{Spread}\)函数,由于其子节点势必要被修改,那么我们也复制一个节点,连接其修改的子节点,然后返回该节点的编号,剩下的函数照常写即可.
值得注意的是,\(\mathrm{Query}\)函数也涉及到了修改,所以也要新建节点. 不过由于其不是实质的修改,所以在查询结束后可以把所有新建的节点回收. 实践证明,使用了节点回收的区间修改主席树,空间常数不会过大,足以解决大部分的问题.
struct Node { int ls,rs; ll sum,tag; Node (void){ ls = rs = sum = tag = 0; } };
struct PresidentTree
{
Node ver[N*25]; int tot,cnt,root[N]; ll a[N];
#define tag(p) ver[p].tag
#define sum(p) ver[p].sum
#define ls(p) ver[p].ls
#define rs(p) ver[p].rs
#define mid ( l + r >> 1 )
#define Ls ls(p) , l , mid
#define Rs rs(p) , mid + 1 , r
inline void Recycle(int l,int r) { for (int i = l + 1; i <= r; i++) ver[i] = Node(); tot = l; }
inline void Update(int p) { sum(p) = sum(ls(p)) + sum(rs(p)); }
inline int Apply(int p,int l,int r,ll v) {
if ( p == 0 ) return 0; int _p = ++tot; ver[_p] = ver[p];
return sum(_p) += 1LL * (r-l+1) * v , tag(_p) += v , _p;
}
inline int Spread(int p,int l,int r) {
int _p = ++tot; ver[_p] = ver[p] , tag(_p) = 0; if ( !tag(p) ) return _p;
return ls(_p) = Apply(Ls,tag(p)) , rs(_p) = Apply(Rs,tag(p)) , _p;
}
inline void Build(int &p,int l,int r) {
p = ++tot; if ( l == r ) return void( sum(p) = a[l] );
return Build(Ls) , Build(Rs) , Update(p);
}
inline int Modify(int p,int l,int r,int ml,int mr,ll v) {
if ( l > r || ml > mr || mr < l || ml > r ) return p;
if ( ml <= l && r <= mr ) return Apply(p,l,r,v); p = Spread(p,l,r);
return ls(p) = Modify(Ls,ml,mr,v) , rs(p) = Modify(Rs,ml,mr,v) , Update(p) , p;
}
inline ll Query(int p,int l,int r,int ql,int qr) {
if ( l > r || ql > qr || qr < l || ql > r ) return 0;
if ( ql <= l && r <= qr ) return sum(p);
return p = Spread(p,l,r) , Query(Ls,ql,qr) + Query(Rs,ql,qr);
}
} T;
以上为\(\mathrm{To\ the\ moon}\)一题的线段树代码,可以同时通过\(\mathrm{SPOJ\ 1536mb}\)和\(\mathrm{Hdu\ 64mb}\)的测试.
动态区间排名
动态区间排名指的是带单点修改的区间第\(k\)大问题,这个经典问题有很多种解决方法.
最常见的三种做法是线段树套平衡树,整体分治,和树状数组套线段树.
首先,我们考虑第一种做法,先对序列建线段树,然后在每一个节点上开一棵平衡树维护该区间所有元素,显然修改操作和插入操作都可以在\(\mathcal{O}(\log^2n)\)的时间内完成. 显然,我们可以查询一个下标区间内小于等于某个值的元素个数,时间复杂度是\(\mathcal{O}(\log^2n)\),那么我们只需要在外层套一个二分答案即可,时间复杂度\(\mathcal{O}(\log^3n)\).
整体分治的做法我们暂不讨论,留到总结分治数据结构的时候再说. 对于维护带修改的前缀和我们容易想到树状数组. 所以我们不妨尝试刚才讨论过的方法,使用树状数组套线段树. 对于一个前缀\([1,x]\),在树状数组上可以用\(\mathcal{O}(\log_2 n)\)棵线段树的并表示,那么区间\([l,r]\)就可以用\(\mathcal{O}(\log_2 n)\)棵线段树的并与另外\(\mathcal{O}(\log_2 n)\)棵线段树的并的差表示. 我们不妨在树状数组里把这些线段树的根先取出来,然后同步遍历他们,使用全局第\(k\)大的做法即可. 时间复杂度为\(\mathcal{O}(\log^2 n)\).
我们不妨转化一下思维,使用树状数组维护值域,线段树维护下标. 那么我们可以直接在树状数组上倍增答案,然后线段树查询区间内的数值个数,时间复杂度和空间复杂度都是一样的.
线段树分治
线段树分治指的是一类以线段树结构来存储修改操作的时间分治技巧. 对于一些难以支持在线操作的动态问题,我们可以对时间线建一棵线段树,叶节点表示某一个具体的时间点.
对于仅在某一时间段出现的操作,我们就把它覆盖到\(\mathcal{O}(\log_2n)\)个线段树节点上,对于某一查询操作,我们把它记到线段树的叶节点上. 最后我们递归遍历线段树,沿路把操作处理掉即可,并在叶节点处回答询问. 不过这时候通常需要用到支持撤回的数据结构维护答案,这里就不多说了.
线段树合并
线段树合并指的是针对两颗维护相同长度序列线段树,求其并集序列的线段树的算法. 该算法很好理解,针对\(\mathrm{Merge}(x,y)\),如果\(x\),\(y\)其一为\(0\),则返回不为零的根,反之则递归合并子树即可. 由于每一次递归会删掉其中一个节点,所以线段树合并的总时间复杂度与一开始所有零散线段树的总点数有关,一般为\(\mathcal{O}(m\log_2n)\),还需视具体情况分析.
inline int Merge(int x,int y)
{
if ( x == 0 || y == 0 ) return x | y; long long s = sum(x) + sum(y);
return ver[x] = { Merge(ls(x),ls(y)) , Merge(rs(x),rs(y)) , s } , x;
}
线段树分裂
线段树分裂是线段树合并的逆过程. 针对一棵线段树,我们可以根据某一标准分裂出它的一个前缀点集及其补集. 例如,我们可以根据点数分裂出一棵权值线段树前\(k\)小的点,那么前\(k\)小的点组成一棵线段树,其他点组成一棵线段树. 代码实现上,我们只要根据分裂标准递归处理左右区间即可,时间复杂度严格\(\mathcal{O}(\log_2 n)\),一次分裂会额外产生\(\mathcal{O}(\log_2n)\)个点.
inline void Split(int x,int &y,long long k)
{
long long t = sum(ls(x)); y = ++tot;
if ( k > t ) Split(rs(x),rs(y),k-t); else swap(rs(x),rs(y));
if ( k < t ) Split(ls(x),ls(y),k); sum(y) = sum(x) - k , sum(x) = k;
}
李超树
一类给定一个二维平面和若干条线段,求整点处线段方程的最大函数值的问题,可以用线段树来维护. 我们对于函数定义域建立线段树,并在每一个线段树区间内存放一条唯一的可能成为最优解的线段. 那么对于任意一个整点处的函数最大值,一定可以在\(\mathcal{O}(\log_2 n)\)个线段树区间上的某个线段处取到,以保证查询复杂度为\(\mathrm{O}(\log_2 n)\).
那么现在的问题就是在某个区间内可能成为最优解的线段有很多,到底保留哪条?既然保证了查询复杂度和正确性,现在我们要尽可能降低插入复杂度. 不妨按照插入顺序考虑:对于一个没有线段的区间,显然直接把当前线段放进去即可. 如果该区间已经有了一条线段,那么我们分两种情况考虑:
\(1.\) 两条线段不相交,那么保留上面那一条线段即可.
\(2.\) 两条线段相交,那么我们显然可以通过计算新线段和旧线段的交点,得知这两条线段分别在该区间的左边多少一长部分,又或者是右边部分多少长一部分更优(它们的优势区间是当且线段树区间的前后缀). 显然,可以保证复杂度的做法是把优势区间长一点的那一条线段保留下来,短一点那条线段放到子区间取递归比较.
根据以上策略,每次下放短一点那条线段的长度就减小了一半,于是下放操作的时间复杂度不超过\(\mathcal{O}(\log_2 n)\),由于有\(\mathcal{O}(\log_2 n)\)个区间需要下放,所以插入一条线段的时间复杂度是\(\mathrm{O}(\log^2 n)\).
由于我们存线段用的是直线方程的斜截式,所以有些时候还需特判直线斜率不存在的情况.
struct Line { double b,k; int id; };
struct LiChaoTree
{
Line ver[N<<2];
#define L(p) ver[p]
#define id(p) ver[p].id
#define mid ( l + r >> 1 )
#define ls p << 1 , l , mid
#define rs p << 1 | 1 , mid + 1 , r
inline double Calc(int x,Line l) { return l.k * x + l.b; }
inline double Inter(Line a,Line b) { return ( b.b - a.b ) / ( a.k - b.k ); }
inline Line Compare(Line x,Line y,int t) { return Calc(t,x) >= Calc(t,y) ? x : y; }
inline void Modify(int p,int l,int r,int ml,int mr,Line x) {
if ( l > r || ml > mr || mr < l || ml > r ) return void();
if ( ml <= l && r <= mr ) {
if ( !id(p) ) return void( L(p) = x ); double vl1,vr1,vl2,vr2;
vl1 = Calc(l,L(p)) , vr1 = Calc(r,L(p)) , vl2 = Calc(l,x) , vr2 = Calc(r,x);
if ( vl1 >= vl2 && vr1 >= vr2 ) return void();
if ( vl1 < vl2 && vr1 < vr2 ) return void( L(p) = x );
if ( vl1 <= vl2 ) return Inter(L(p),x) <= mid ?
Modify(ls,ml,mr,x) : ( swap(L(p),x) , Modify(rs,ml,mr,x) );
if ( vl1 > vl2 ) return Inter(L(p),x) <= mid ?
( swap(L(p),x) , Modify(ls,ml,mr,x) ) : Modify(rs,ml,mr,x);
}
return Modify(ls,ml,mr,x) , Modify(rs,ml,mr,x);
}
inline Line Query(int p,int l,int r,int x) {
Line res = ver[p]; if ( l == r ) return res;
return Compare( res , x <= mid ? Query(ls,x) : Query(rs,x) , x );
}
} T;

 数据结构总结第二篇
数据结构总结第二篇

