『数据结构总结1:树状数组』
『数据结构总结1:树状数组』
Preface
数据结构的总结可能就会以这种形式分好几篇发了,吸取了之前的教训,防止编辑器变卡.
如果后继总结更新了,链接会补在这里.
原理
树状数组是一种用于维护序列前缀和的数据结构,对于给定序列\(\{a_i\}\),建立序列\(\{c_i\}\)定义如下:
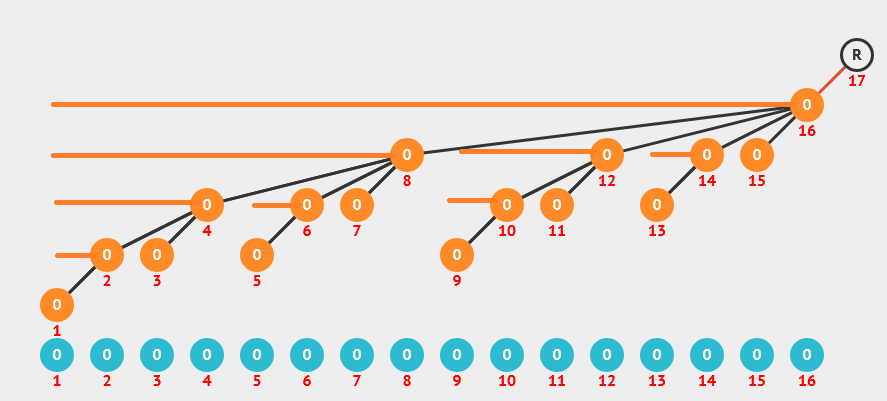
对于一个任意的正整数\(n\),我们都可以根据其二进制上为\(1\)的位,利用\(\mathrm{lowbit}\)运算,将\([1,n]\)划分为不超过\(\log_2 n\)个区间. 那么前缀和就可以用这\(\log_2n\)个区间和的和表示,根据序列\(\{c_i\}\)的定义,我们可以轻松地在\(\mathcal{O}(\log_2n)\)的时间内求一个序列的前缀和.
对于单点修改,我们只需考察那些\(c_x\)会被当前修改的值所影响. 我们可以将\(\{c_i\}\)看做一个树形结构(森林),每个点\(c_i\)占据区间\([i-\mathrm{lowbit}(i)+1,i]\),同时向其内部所有最大的,可以表示其区间和的\(c_j\)连边. 那么显然一个点的修改会对树上所有祖先有影响,同时不难发现一个性质节点\(c_i\)的父亲为\(c_{i+\mathrm{lowbit(i)}}\),那么修改操作就容易实现了. 根据\(\mathrm{lowbit}\)函数的性质,其时间复杂度显然也是\(\mathcal{O}(\log_2 n)\).
实现
struct BinaryIndexedTree
{
int c[N],n;
inline int lowbit(int x) { return x & (-x); }
inline void Modify(int p,int v) { for (; p <= n; p += lowbit(p)) c[p] += v ); }
inline int Query(int p) { int s = 0; for (; p; p -= lowbit(p)) s += c[p]; return s; }
inline int Query(int l,int r) { return Query(r) - Query(l-1); }
}
不必过多解释,唯一需要注意的地方是\(\mathrm{lowbit}(0)=0\),所以单点修改时如果涉及到下标\(0\),需要进行整体平移,否则会死循环.
功能
单点修改,区间查询
基本操作,时间复杂度均为\(\mathcal{O}(\log_2n)\).
区间修改,单点查询
不妨对原序列进行差分,那么在原序列上的操作\((l,r,+x)\)对差分序列\(\{d_n\}\)的影响为\(l\)位置\(+x\),\(r+1\)位置\(-x\). 单点查询在差分序列上的体现为前缀和.
区间修改,区间查询
同样求其差分序列\(\{d_n\}\),修改操作同上执行. 我们只需考虑如何求和:
维护\(\{d_i\}\)和\(\{d_i\times i\}\)两个前缀和即可.
后缀操作
将修改函数和求和函数的遍历顺序反过来即可.
区间修改,区间最值
类似于线段树,从\(\mathcal{O}(\log_2n)\)个儿子处获取信息,并下传懒标记,时间复杂度\(\mathcal{O}(\log^2 n)\),无实际意义.
当操作只有单点修改,前缀最值\(/\)后缀最值查询时,可以直接按照原来的方式处理,时间复杂度\(\mathcal{O}(\log_2n)\).
维护二维平面
定义
其他概念类似,可以用完全一样的方式实现单点修改,矩阵求和,时间复杂度\(\mathcal{O}(\log^2 n)\),空间复杂度\(\mathcal{O}(n^2)\).
定义二维差分\(d_{i,j}=a_{i,j}-a_{i-1,j}-a_{i,j-1}+a_{i-1,j-1}\),显然满足\(a_{n,m}=\sum_{i=1}^n\sum_{j=1}^m d_{i,j}\). 现对原矩阵差分,则矩阵修改\((x_1,x_2,y_1,y_2,+p)\)在差分矩阵上的影响为\((x_1,y_1,+p),(x_1,y_2+1,-p),(x_2+1,y_1,-p),(x_2+1,y_2+1,+p)\). 那么容易实现矩阵修改,单点查询.
现在我们用差分实现矩阵修改,同理,考虑用差分矩阵的值表示原矩阵的一个前缀矩阵和:
维护\(\{d_{i,j}\}\),\(\{i\times d_{i,j}\}\),\(\{j\times d_{i,j}\}\),\(\{i\times j\times d_{i,j}\}\)四个矩阵和即可实现矩阵修改,矩阵查询.
值域树状数组
值域树状数组可以实现简易平衡树的功能,维护排名就是前缀和,插入删除一个数字就是单点修改,现在我们考虑求\(k\)大值.
考虑倍增,每次我们尝试向前\(2^i\)走步,\(i\)从大到小枚举. 现在假设答案为\(p\),那么我们想知道区间\([k,k+2^i]\)里有几个数. 如果有\(i<\mathrm{lowbit}(k)\),那么根据定义\(c_{k+2^i}\)存储的就是我们要的值. 好在倍增算法从大到小枚举\(i\),所以\(k\)累加的过程也是从高位到低位的,恰好符合我们的需求. 那么倍增求第\(k\)大,时间复杂度\(\mathcal{O}(\log_2 n)\).
inline int Select(int k)
{
int res = 0 , cnt = 0;
for (int i = 30; res += (1<<i) , i >= 0; i--)
( res > lim || cnt + c[res] >= k ) ? res -= 1<<i : cnt += c[res];
return ++res; // if the size of BIT less than k , return size + 1
}

 数据结构总结第一篇
数据结构总结第一篇

