『组合数学总结1：基础组合数学和组合原理』

Preface

前排提示：本文数学公式较多，加载\(\LaTeX\)需要一定时间，可能会导致浏览器暂时卡顿，请耐心等待数学公式正常显示.

组合数学知识点的总结，本来准备写在一起的，结果发现字数有点多，导致\(\mathrm{markdown}\)编辑器频繁卡顿，那就分三篇发布好了.

\(\mathrm{Update}\)：目前第一篇就是组合基础和组合原理，预计第二篇基础高数，生成函数和特殊计数数列，第三篇多项式算法，至于会不会咕咕咕那就不知道了.

基本组合数学

一些定义和符号

\(1.\) 用\(n!\)表示\(n\)的阶乘，\(n!=1\times 2\times \cdots \times n\)，用\(n^{\underline k}\)表示下降阶乘幂，简称下降幂，\(n^{\underline k}=n\times (n-1)\times \cdots \times (n-k+1)\)，用\(n^{\overline k}\)表示上升阶乘幂，简称上升幂，\(n^{\overline k}=n\times (n+1)\times \cdots\times (n+k-1)\).

\(2.\) 用\(\mathrm{A}_n^m\)表示从\(n\)个元素种选出\(m\)个组成的排列数量，称为排列数，\(\mathrm{A}_n^m=\frac{n!}{(n-m)!}\).

\(3.\) 用\(\mathrm{C}_n^m\)或\({n \choose m}\)表示从\(n\)个元素种选出\(m\)个组成的子集数量，称为组合数，\(\mathrm{C}_n^m={n\choose m}=\frac{n!}{m!(n-m)!}\).

\(4.\) 下降阶乘幂\(n^{\underline k}\)种\(n\)可以是任意实数，当我们将组合数\({r\choose k}\)定义改为\({r\choose k}=\frac{r^{\underline k}}{k!}\)时，称其为二项式系数，其中上指标可以为任意实数，下指标仍为整数，当下指标\(k<0\)时，二项式系数的值为\(0\).

计数原理和计数方法

计数原理

\(1.\) 加法原理：如果完成一件事情有\(n\)类方法，且第\(i\)类方法有\(a_i\)种方案，则完成这件事情共有\(\sum a_i\)种方案。

\(2.\) 乘法原理：如果完成一件事情有\(n\)个步骤，且第\(i\)个步骤有\(a_i\)种方案，则完成这件事情共有\(\prod a_i\)种方案。

计数方法

\(1.\) 相邻元素捆绑法

例：现有\(7\)人站成一排，其中甲乙相邻且丙丁相邻，共有多少种不同的排法？

将甲乙两元素捆绑成整体并看成一个复合元素，同时丙丁也看成一个复合元素，再与其它元素进行排列. 因此方案数为\(\mathrm{A}_5^5\times \mathrm{A}_2^2\times \mathrm{A}_2^2=480\)种.

\(2.\) 不相邻元素插空法

例：现有\(4\)个\(A\)球，\(2\)个\(B\)球，\(3\)个\(C\)球，把它们排成一排，所有\(A\)球不能相邻，且所有的球都是可分辨的，求有多少种排法？

先把\(B,C\)球排好，此时出现了\(6\)个间隙，把\(A\)球插入这些间隙即可. 因此方案数为\(\mathrm{A}_5^5\times \mathrm{A}_6^4=43200\)种.

\(3.\) 相同元素隔板法

例：把\(10\)个完全相同的球放入\(7\)个盒子中，每个盒子至少放一个，求有多少种方案？

因为球是相同的，所以可以将球先随意地排成一行，此时球与球之间出现了\(9\)个间隙，插入\(6\)个板就可以做到把球分割为\(7\)个非空部分的效果. 因此方案数为\({9 \choose 6}=84\)种.

重要的组合恒等式

对称恒等式

\[{n \choose k}={n\choose {n-k}} \]

对于\(n,k\in \Z,n\geq 0\)成立.

证明：根据定义阶乘展开即可.

吸收/提取恒等式

\[{r \choose k}=\frac{r}{k}{r-1\choose k-1} \]

对于\(r\in \R,k\in \Z\)且\(k\not = 0\)成立.

证明：$$\binom{r}{k}=\frac{r^{\underline{k}}}{k!}=\frac{r}{k}\times \frac{(r-1)^{\underline{k-1}}}{(k-1)!}=\frac{r}{k}\binom{r-1}{k-1}$$

加法/归纳恒等式

\[{r \choose k}={r-1\choose k}+{r-1\choose k-1} \]

对于\(r\in \R,k \in \Z\)成立.

证明：

\[\binom{r-1}{k-1}+\binom{r-1}{k}=\frac{(r-1)^{\underline{k-1}}}{(k-1)!}+\frac{(r-1)^{\underline{k}}}{k!}\\ \ \\=\frac{k(r-1)^{\underline{k-1}}}{k!}+\frac{(r-k)(r-1)^{\underline{k-1}}}{k!}=\frac{r^{\underline{k}}}{k!}=\binom{r}{k} \]

相伴恒等式

\[(r-k){r\choose k}=r{r-1\choose k},k{r\choose k}=(r-k+1){r\choose k-1} \]

对于\(r\in \R,k\in \Z\)成立.

证明：

\[(r-k)\binom{r}{k}=\frac{r!}{(r-k-1)!k!}=r\times \frac{(r-1)^{\underline{r-k-1}}}{(r-k-1)!}\\\ \\=r\binom{r-1}{r-k-1}=r\binom{r-1}{k} \\\ \\ k{r\choose k}=\frac{r^{\underline k}}{(k-1)!}=\frac{(r-k+1)r^{\underline{k-1}}}{(k-1)!}=(r-k+1){r\choose k-1}\]

上指标反转

\[{r\choose k}=(-1)^{k}{r-k-1\choose k} \]

对于\(r\in \R,k \in \Z\)成立.

证明：

\[\binom{r}{k}=\frac{r^{\underline{k}}}{k!}\\ \ \\ =\frac{r\times (r-1) \times ... \times (r-k+1)}{k!}\\ \ \\ =\frac{(-1)^{k}\times (k-r-1)\times (k-r-2) \times ... \times (-r)}{k!}\\ \ \\ =(-1)^k\frac{(r-k-1)^{\underline{k}}}{k!}=(-1)^k\binom{r-k-1}{k} \]

三项式系数恒等式

\[{r\choose m}{m\choose k}={r\choose k}{r-k\choose m-k} \]

对于\(r\in \R, m,k\in \Z\)成立.

证明：

\[\binom{r}{m}\binom{m}{k}=\frac{r!}{(r-m)!(m-k)!k!}=\binom{r-k}{m-k}\binom{r}{k} \]

上指标求和

\[\sum_{i=m}^n{i\choose m}={n+1\choose m+1} \]

对于\(n,m\in \Z\)成立.

证明：

设有\(n+1\)个物品，标号为\(1\sim n+1\)，现在从中选取\(m+1\)个物品的方案数即为\({n+1\choose m+1}\)，同时等价于在\(n\)个物品每个物品后插入一个结束符，强选结束符并在结束符前选\(m\)个物品的方案数。

平行恒等式

\[\sum_{i=0}^n\binom{m+i}{i}=\binom{m+n+1}{n} \]

对于\(n,m\in \Z\)成立。

证明：

\[\sum_{i=0}^n\binom{m+i}{i}=\sum_{i=0}^n\binom{m+i}{m}\\ \ \\ =\sum_{i=m}^{n+m}\binom{i}{m}=\binom{n+m+1}{m+1}=\binom{n+m+1}{n} \]

范德蒙德卷积/下指标卷积

\[\sum_{k=0}^n\binom{r}{k}\binom{s}{n-k}=\binom{r+s}{n} \]

对于\(r,s\in \R , n\in \Z\)成立。

证明：

左边表示从\(r\)个男生中选\(k\)个人，从\(s\)个女生中选出\(n-k\)个人的方案数，求和即为在\(r+s\)个人中选\(n\)个人的方案数，可知：\(\sum_{k=0}^n\binom{r}{k}\binom{s}{n-k}=\binom{r+s}{n}\)。

下指标点积

\[\sum_{i=0}^{m}{n\choose i}{m\choose i}={n+m\choose m} \]

假设\(m<n\)，则对于\(n,m\in \Z\)成立.

证明：

\[\sum_{i=0}^{m}{n\choose i}{m\choose i}=\sum_{i=0}^{m}{n\choose i}{m\choose m-i}={n+m\choose m} \]

上指标卷积

\[\sum_{i=0}^n{i\choose a}{n-i\choose b}={n+1\choose a+b+1} \]

对于\(n,a,b\in \Z\)成立.

证明：考虑左式的组合意义为将\(n\)个物品分为在左右两部分，左边选\(a\)个，右边选\(b\)个的方案数，同时等价于插入一个分隔符，共\(n+1\)个物品选\(a+b+1\)个的方案数.

• 上指标求和和上指标卷积同样存在非组合意义的直接证明方式，而范德蒙德卷积存在生成函数的证明方式，这保证了它们的绝对正确性.

二项式定理相关

二项式定理

根据二项式定理，组合数可以作为二项式高次幂展开式的系数：

\[(x+y)^n=\sum_{i=0}^{n}{n\choose i}x^iy^{n-i} \]

该式被称作二项式定理.

证明：

根据数学归纳法，该式在\(n=1\)时显然成立，那么假设其在\(n=p-1(p\geq 2)\)时也成立，则有：

\[(x+y)^p=(x+y)^{p-1}(x+y)=(x+y)\sum_{i=0}^{p-1}{p-1\choose i}x^iy^{p-1-i} \\ \ \\ =\sum_{i=0}^{p-1}{p-1\choose i}x^{i+1}y^{p-1-i}+\sum_{i=0}^{p-1}{p-1\choose i} x^iy^{p-i} \\ \ \\ =\sum_{i=1}^p{p-1\choose i-1}x^iy^{p-i}+\sum_{i=0}^{p-1}{p-1\choose i}x^iy^{p-i} \\ \ \\ =\sum_{i=0}^p\left( {p-1\choose i-1}+{p-1\choose i}\right)x^i y^{p-i}=\sum_{i=0}^p{p\choose i}x^iy^{p-i} \]

可知对于\(n=p\)，该式也成立，故对于所有\(n\in \N^+\)，定理都成立.

二项式定理的推广

由于二项式系数的上指标可以是任意实数，所以二项式定理也有推广形式：

\[(x+y)^{\alpha}=\sum_{i=0}^{\infty}{\alpha \choose i}x^{i}y^{\alpha -i} \]

其中\(\alpha \in \R\)，称为广义二项式定理.

• 事实上，我们还需考虑右式的收敛性，不过在应用中完全不需要理会这点.

对于阶乘幂，二项式定理仍成立：

\[(x+y)^{\underline n}=\sum_{i=0}^n{n\choose i}x^{\underline i}y^{\underline {n-i}} \\ \ \\ (x+y)^{\overline n}=\sum_{i=0}^n{n\choose i}x^{\overline i}y^{\overline {n-i}}\]

证明略.

二项式定理的直接推论

\(1. \sum_{i=0}^n {n\choose i}=(1+1)^n=2^n\)

\(2. \sum_{i=0}^n{n\choose i}[2|i]=\sum_{i=1}^n{n\choose i}[2\not | i]=2^{n-1}\)

证明：

首先\(n\)个数中选奇数个数和选偶数的数的方案肯定是一样的.那么考虑选偶数个数的方案：单独考虑最后一个数，若选，则还需在\(n-1\)个数中选奇数个数，若不选，则还需选偶数个数，问题转回到推论一，答案即为\(2^{n-1}\).

\(3. \sum_{i=0}^n(-1)^i{n\choose i}=(1-1)^n=[n=0]\)

多项式定理

定义多项式系数$$\binom{n_1+n_2+\cdots+n_k}{n_1,n_2,\cdots,n_k}=\frac{(n_1+n_2+\cdots+n_k)!}{n_1!n_2!\cdots n_k!}$$

则有如下的多项式定理成立：

\[\left(\sum_{i=1}^kx_i\right)^n=\sum_{\sum_{i=1}^{k}n_i=n}\binom{n_1+n_2+\cdots+n_k}{n_1,n_2,\cdots,n_k}\prod_{i=1}^kx_i^{n_i} \]

证明可以直接从组合角度考虑.

模域组合数的计算

预处理杨辉三角的方法

杨辉三角是二项式系数在三角形中的一种几何排列，由中国数学家杨辉提出. 形式化地，杨辉三角可以表示成如下的下三角矩阵：

\[\left[ \begin{matrix} {0\choose 0} & 0 & 0 & 0 & \cdots\\ {1\choose 0} & {1\choose 1} & 0 & 0 & \cdots \\ {2\choose 0} & {2\choose 1} & {2\choose 2} & 0 & \cdots \\ {3\choose 0} & {3\choose 1} & {3\choose 2} & {3\choose 3} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{matrix} \right] \]

其中\(A_{i,j}\)表示杨辉三角的第\(i\)行第\(j\)个数，有\(A_{i,j}={i\choose j}\). 杨辉三角满足\(A_{i,j}=A_{i-1,j}+A_{i-1,j-1}\)，本质上是组合数的加法恒等式.

那么我们可以根据加法恒等式预处理一张\(n^2\)大小的杨辉三角形的表，\(O(1)\)回答组合数。

对模数没有任何要求，时间复杂度\(O(n^2)-O(1)\).

#include <bits/stdc++.h>
using namespace std;
const int N = 5020;
int C[N][N],n,Mod;
inline int inc(int a,int b) { return a + b >= Mod ? a + b - Mod : a + b; }
inline void Init(void)
{
    C[0][0] = C[1][0] = C[1][1] = 1;
    for (int i = 2; i <= n; i++)
    {
        C[i][0] = C[i][i] = 1;
        for (int j = 1; j < i; j++)
            C[i][j] = inc( C[i-1][j] , C[i-1][j-1] );
    }
}

预处理阶乘的方法

计算模意义下的组合式最常用的方法就是根据组合数的阶乘展开式计算。我们可以\(O(n)\)预处理阶乘，并用费马小定理求出最大数值阶乘的逆元，倒序更新所有阶乘的逆元，就可以实现\(O(1)\)回答组合数.

此时要求模数\(p\)为大于\(n,m\)的质数，换言之，\(1\sim \max(n,m)\)的阶乘在模\(p\)意义下均存在逆元时，该方法有效，时间复杂度\(O(n)-O(1)\).

#include <bits/stdc++.h>
using namespace std;
const int Mod = 1e9 + 7 , N = 1e6 + 20;
inline int inc(int a,int b) { return a + b >= Mod ? a + b - Mod : a + b; }
inline int dec(int a,int b) { return a - b < 0 ? a - b + Mod : a - b; }
inline int mul(int a,int b) { return 1LL * a * b % Mod; }
inline void Inc(int &a,int b) { return void( a = inc( a , b ) ); }
inline void Dec(int &a,int b) { return void( a = dec( a , b ) ); }
inline void Mul(int &a,int b) { return void( a = mul( a , b ) ); }
inline int fastpow(int a,int b) { int res = 1; for (; b; Mul(a,a),b>>=1) if (b) Mul(res,a); return res; }
inline int Inv(int x) { return fastpow( x , Mod - 2 ); }
int inv[N],fac[N];
inline void Init(void)
{
    inv[0] = fac[0] = 1;
    for (int i = 1; i <= N - 20; i++) fac[i] = mul( fac[i-1] , i );
    inv[ N - 20 ] = Inv( fac[ N - 20 ] );
    for (int i = N - 21; i >= 1; i--) inv[i] = mul( inv[i+1] , i+1 );
}
inline int C(int n,int m) { return ( m > n || n < 0 || m < 0 ) ? 0 : mul( fac[n] , mul( inv[m] , inv[n-m] ) ); }

Lucas定理

当模数\(p\leq\max(m,n-m)\)时，组合数分母的\(m!(n-m)!\)就不存在逆元，此时我们需要用到\(\mathrm{Lucas}\)定理：

\[{n\choose m}\equiv {n\bmod p\choose m\bmod p}\times {\left\lfloor\frac{n}{p}\right\rfloor\choose\left\lfloor\frac{m}{p}\right\rfloor}\pmod p \]

证明：

引理：\((1+x)^p\equiv1+x^p\pmod p,p\in \mathrm{Prime}\).

有费马小定理可知\((1+x)^p\equiv1+x\)，又因为\(x\equiv x^p\)，可知\((1+x)^p\equiv 1+x^p\).

\[(1+x)^n\equiv(1+x)^{\left\lfloor\frac{n}{p}\right\rfloor p}(1+x)^{n\bmod p}\pmod p \\ \ \\ (1+x)^n\equiv (1+x^p)^{\left\lfloor\frac{n}{p}\right\rfloor}(1+x)^{n\bmod p}\pmod p\]

用二项式定理展开上式中的三个二项式的幂：

\[\sum_{i=0}^n{n\choose i}x^i\equiv\sum_{j=0}^{\left\lfloor\frac{n}{p}\right\rfloor}{\left\lfloor\frac{n}{p}\right\rfloor\choose j}(x^p)^{j} \times\sum_{k=0}^{n\bmod p}{n\bmod p\choose k}x^k \]

左式取到\(x^m\)项系数为\({n\choose m}\)，右式取到\(x^m\)项系数当且仅当\(j=\left\lfloor\frac{m}{p}\right\rfloor,k=m\bmod p\)，对应项系数同余，所以就有：

\[{n\choose m}\equiv {n\bmod p\choose m\bmod p}\times {\left\lfloor\frac{n}{p}\right\rfloor\choose\left\lfloor\frac{m}{p}\right\rfloor}\pmod p \]

• 另一种理解，\(\mathrm{Lucas}\)定理的含义即为将组合数拆解为\(n,m\)按照\(p\)进制分解后每一位的组合数之积

回到上文，对于模数\(p\)较小时，只要\(p\)为质数，我们就可以运用\(\mathrm{Lucas}\)定理递归求解组合数，时间复杂度\(O(p)-O(\log_{p}n)\).

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 20;
int inv[N],fac[N],n,m,Mod,T;
inline int inc(int a,int b) { return a + b >= Mod ? a + b - Mod : a + b; }
inline int dec(int a,int b) { return a - b < 0 ? a - b + Mod : a - b; }
inline int mul(int a,int b) { return 1LL * a * b % Mod; }
inline void Inc(int &a,int b) { return void( a = inc( a , b ) ); }
inline void Dec(int &a,int b) { return void( a = dec( a , b ) ); }
inline void Mul(int &a,int b) { return void( a = mul( a , b ) ); }
inline int fastpow(int a,int b) { int res = 1; for (; b; Mul(a,a),b>>=1) if (b) Mul(res,a); return res; }
inline int Inv(int x) { return fastpow( x , Mod - 2 ); }
inline void Init(void)
{
    inv[0] = fac[0] = 1;
    for (int i = 1; i <= Mod - 1; i++) fac[i] = mul( fac[i-1] , i );
    inv[Mod-1] = Inv( fac[Mod-1] );
    for (int i = Mod - 2; i >= 1; i--) inv[i] = mul( inv[i+1] , i+1 );
}
inline int C(int n,int m) { return ( m > n || n < 0 || m < 0 ) ? 0 : mul( fac[n] , mul( inv[m] , inv[n-m] ) ); }
inline int Lucas(int n,int m) { return m == 0 ? 1 : mul( C(n%Mod,m%Mod) , Lucas(n/Mod,m/Mod) ); }
int main(void)
{
    scanf( "%d" , &T );
    while ( T --> 0 )
        scanf( "%d%d%d" , &n , &m , &Mod ),
        Init() , printf( "%d\n" , Lucas(n+m,n) );
    return 0;
}

常见的组合问题

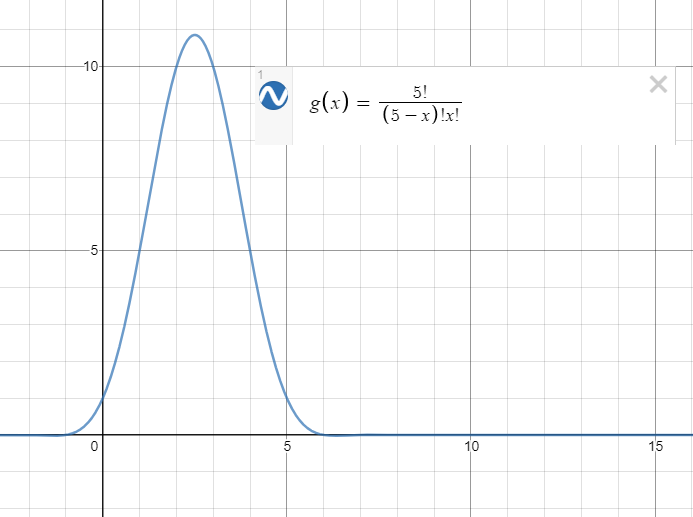
组合数的单调性

对于上指标确定的组合数，我们可以令\(f(x)={n\choose x}(n\in \N ^ +)\)，则函数\(f\)是单峰函数，其极值在\(x=\lfloor \frac{n}{2} \rfloor\)处取到.

图：用连续函数的图像近似离散函数的图像

阶乘幂反转

两类阶乘幂可以提取因数\(-1\)进行互相转换：

\[x^{\underline{n}}=(-1)^n(x-n+1)^{\underline{n}},x^{\overline{n}}=(-1)^n(1-x-n)^{\overline{n}} \]

循环排列

从\(n\)个元素中选出\(m\)个排成圆圈的方案数，相当于线性排列时固定第一个数的方案。

一个循环排列可以对应\(m\)个线性排列，进而可以得到循环排列的计算公式：

\[\mathrm{Cir}_{n}^{m}=\frac{A_{n}^{m}}{m}=\frac{n!}{m\times (n-m)!} \]

组合数的数论性质

若\(p\)为质数，则对于\(n\in[1,p-1]\)，有\(p\ |\ \binom{p}{n}\)。

证明：

\[\because \binom{p}{n}=\frac{p\times (p-1)\times ... \times (p-n+1)}{n!}\in \Z\\ \ \\ \therefore n!\ |\ p\times (p-1) \times ... \times (p-n+1)\\ \ \\ \because(p,n)=1\\ \ \\ \therefore n!\ |\ (p-1) \times (p-1) \times ... \times (p-n+1)\\ \ \\ \therefore p\ |\ \binom{p}{n} \]

不定方程的解数问题

\(1.\) 正整数解

求不定方程\(x_1+x_2+\cdots+x_k=n\)的正整数解的个数。

这个问题等价于把\(n\)个球放入\(k\)个盒子中，每个盒子中至少有\(1\)个球，由隔板法可知其方案数为\(\binom{n-1}{k-1}\)。

\(2.\) 非负整数解

求不定方程\(x_1+x_2+\cdots+x_k=n\)的非负整数解的个数。

我们可以新增\(k\)个球，这样问题就等价于把\(n+k\)个球放入\(k\)个盒子中，每个盒子中至少有\(1\)个球，由隔板法可知其方案数为\(\binom{n+k-1}{k-1}\)。

\(3.\) 下界限制

求不定方程\(x_1+x_2+\cdots+x_k=n\)的整数解的个数，满足\(x_1\geq a_1,x_2\geq a_2,\cdots,x_k\geq a_k\)。

这个问题等价于不定方程\(x_1+x_2+\cdots+x_k=n-a_1-a_2-\cdots-a_k\)的非负整数解个数，可以其方案数为$$\binom{n+k-1-\sum_{i=1}^{n}a_i}{k-1}$$

\(4.\) 上下界限制

求不定方程\(x_1+x_2+\cdots+x_k=n\)的整数解的个数，满足\(a_1\leq x_1\leq b_1,a_1\leq x_2\leq b_2,\cdots,a_k\leq x_k\leq b_k\)。

首先把限制转换为\(0\leq x_1\leq b_1-a_1,\cdots,0\leq x_k\leq b_k-a_k\)，运用容斥原理，答案即为：

\[\sum_{S\subseteq \{1,2,\cdots,k\}}(-1)^{|S|}\binom{n-1-\sum_{x\in S}(b_x-a_x)}{k-1} \]

多重集排列数

多重集指含有重复元素的广义集合。设多重集\(S=\{n_1\times a_1,n_2\times a_2,\cdots,n_k\times a_k\}\)是由\(n_1\)个\(a_1\)，\(n_2\)个\(a_2\)，\(...\)，\(n_k\)个\(a_k\)组成的集合，则\(S\)的全排列个数为

\[\frac{\left (\sum_{i=1}^k n_i\right)!}{\prod_{i=1}^k\left (n_i!\right)} \]

证明：

对于朴素全排列，显然有\(\left (\sum_{i=1}^k n\right )!\)种方案，而在多重集的排列过程中，每个\(a_i\)出现了\(n_i\)次，在这\(n_i\)个位置间各个\(a_i\)可以互相调换位置，有\(n_i!\)中方案，故除去每一个\(n_i\)可以调换位置的重复方案即为总排列数.

多重集的组合数

设多重集\(S=\{n_1\times a_1,n_2\times a_2,\cdots,n_k\times a_k\}\)是由\(n_1\)个\(a_1\)，\(n_2\)个\(a_2\)，\(...\)，\(n_k\)个\(a_k\)组成的集合，从中取出\(r\left(r\leq\sum_{i=1}^{k}n_i\right)\)个元素可以组成不同集合个数为：

\[\tbinom{k+r-1}{k-1}-\sum_{i=1}^n\tbinom{k+r-n_i-2}{k-1}+\sum_{1\leq i\leq j\leq n}\tbinom{k+r-n_i-n_j-3}{k-1}-\cdots+(-1)^k\tbinom{k+r \sum_{i=1}^k n_i- k-1}{k-1} \]

证明：

首先考虑\(r\leq\min\{n_i\}\)的情况，根据不定方程的非负整数解数量，可知答案为\({k+r-1\choose k-1}\).

然后可以考虑容斥原理，对于\(i\)，让选择\(a_i\)个数超出\(n_i\)成为一个性质，那么不具备任何性质的方案数即为上式.

高阶差分

定义离散函数的差分算子\((\Delta a)_i=a_i-a_{i-1}\)，则有：

\[(\Delta^{n}a)_i=\sum_{j=0}^n(-1)^j{n\choose j}a_{i-j} \]

证明：

容易在算子间定义四则运算，此处不再赘述.

定义平移算子\((\mathrm{E}a)_i=a_{i-1}\)，恒等算子\((\mathrm{I}a)_i=a_i\)，那么就有\(\Delta =\mathrm{I-E}\).

根据二项式定理展开：

\[\Delta^n=(\mathrm{I-E})^n=(-1)^n\sum_{j=0}^n{n\choose j}\mathrm{E}^j(-\mathrm{I})^{n-j} \]

取第\(i\)项就可以得到：

\[(\Delta^{n}a)_i=(-1)^n\sum_{j=0}^n(-1)^{n-j}{n\choose j}a_{i-j} =\sum_{j=0}^n(-1)^j{n\choose j}a_{i-j}\]

可以用多项式卷积算法求高阶差分序列的前\(n\)项.

下指标求和（HDU6333）

对于组合数的下指标求和，即：

\[\sum_{i=0}^m{n\choose i} \]

没有很好的封闭形式解，但是对于多组\((n,m)\)的询问，我们可以将\(n,m\)看作一个区间的左右端点，使用\(O(\max\{n_i,m_i\}\sqrt q)\)的莫队算法来求解.

考虑转移，对于\(m\rightarrow m+1\)，只需加上一个组合数\({n\choose m+1}\)即可. 对于\(n\rightarrow n+1\)，我们可以考虑用加法公式进行拆解：

\[\sum_{i=0}^m{n+1\choose i}=\sum_{i=0}^m\left({n\choose i}+{n\choose i-1}\right)=\sum_{i=0}^m{n\choose i}+\sum_{i=0}^{m-1}{n\choose i} \\ \ \\ =2\sum_{i=0}^m{n\choose i}-{n\choose m}\]

于是区间移动可以\(O(1)\)处理了.

自然数幂和

自然数幂和指的是这一类求和问题：

\[\mathrm{S}_k(n)=\sum_{i=1}^ni^k \]

对于\(k\)比较小的情况，可以用组合恒等式推出通项公式.

\[k=1,\mathrm S_1(n)=\frac{n\times (n+1)}{2} \]

\[k=2,\mathrm S_2(n)=\sum_{i=1}^ni+2\sum_{i=1}^n{i\choose 2}=\frac{n\times (n+1)\times (2n+1)}{6} \]

\[k=3,\mathrm S_3(n)=\sum_{i=1}^ni+6\sum_{i=1}^n{i+1\choose 3}=\frac{n^2\times (n+1)^2}{4} \]

• 不难发现，\(k\)次多项式的求和式都可以表示为\(k+1\)次多项式.

对于\(k\)任意的情况，我们很难直接推出通项公式，但是可以通过多项式插值技巧求出答案，我们会在下文讨论这个问题.

组合原理

鸽巢原理

普通鸽巢原理

鸽巢原理又称抽屉原理，形式化表述如下：

• 设\(q_1,q_2,q_3,\cdots,q_n\)是正整数，如果将\(\sum q_i-n+1\)个物品放入\(n\)个盒子中，记第\(i\)个盒子里放了\(a_i\)个物品，则总存在一个盒子\(j\)，满足\(a_j\geq q_j\).

证明：

反证法，若不存在这样的盒子\(j\)，则对于任意的\(i\)都有\(a_i<q_i\)，那么\(\sum a_i\leq \sum(q_i-1)<\sum q_i -n+1\)，与总球数为\(\sum q_i - n + 1\)矛盾.

应用\(1\)：每十三个人中，总存在两人出生在同一个月.

证明：显然.

应用\(2\)：对于序列\(a_{1\sim n}\)，总存在区间\([l,r]\)使得\(n|\sum_{i=l}^ra_i\) .

证明：记其前缀和为数组\(s_{0\sim n}\)，共有\(n+1\)个元素，所以必定存在\(i,j\)满足\(s_i\equiv s_j\pmod n\)，于是令\(l=i-1,r=j\)即可.

平均值原理

对于\(n\)个变量\(x_1,x_2,\cdots,x_n\)，总满足：

\[\min_{i=1}^n\{a_i\}\leq\frac{\sum_{i=1}^na_i}{n}\ ,\ \max_{i=1}^n\{a_i\}\geq\frac{\sum_{i=1}^na_i}{n} \]

证明：反证法，导出矛盾.

Ramsey定理

对于正整数\(n,m\)，总存在确定的上界\(x\)，满足对\(\mathrm{K}_x\)中所有边随意黑白染色，其中要么包含黑色\(\mathrm{K}_n\)，要么包含白色\(\mathrm{K}_m\). 可以记\(x=\mathrm{R}(n,m)\)，称为\(\mathrm{Ramsey}\)数.

证明略.

实例：\(\mathrm{R}(3,3)=6\). 可以考虑第一个点的五条边，根据鸽巢原理，总存在三条边同色，那么三条同色边连接的三个点要么构成同色\(\mathrm{K}_3\)，要么与第一个点构成另一种同色\(\mathrm{K}_3\).

\(\mathrm{Ramsey}\)定理在高维情况下仍然成立，即：

\[\mathrm{R}(a_1,a_2,\cdots,a_n)<\infty \]

反演原理

反演的实质

对于形如下的式子，我们称左右两式互为反演式：

\[f_i=\sum_{j=1}^iA_{i,j}g_j\Leftrightarrow g_i=\sum_{j=1}^iB_{i,j}f_j\tag 0 \]

我们可以把\(f,g\)看作只有一行的矩阵，于是反演原理本质上就是矩阵乘法求逆：

\[f=g\times A\Leftrightarrow g=f\times B \]

• 我们还可以发现\(A,B\)都是下三角矩阵.

不过矩阵乘法并没有什么用，我们可以根据反演式倒推反演成立的充要条件. 方法其实很简单，我们可以将右式的表达式带入到左式里面，如果最后化简得到了恒等式，那就说明右式可以推导得到左式.

同理，我们再把左式带到右式里面，然后化简得到恒等式，才能说明反演成立.

那么我们来实操一下：

\[f_i=\sum_{j=1}^iA_{i,j}\sum_{k=1}^jB_{j,k}f_k \\ \ \\ f_i=\sum_{k=1}^if_k\left(\sum_{j=k}^iA_{i,j}B_{j,k}\right)=\sum_{k=1}^if_k[k=i]\]

于是就有了右边推左边的条件：

\[\sum_{j=k}^iA_{i,j}B_{j,k}=[k=i]\tag{1} \]

同理把左边代入右边：

\[g_i=\sum_{j=1}^iB_{i,j}\sum_{k=1}^j A_{j,k}g_k \\ \ \\ g_i=\sum_{k=1}^ig_k\left(\sum_{j=k}^iB_{i,j}A_{j,k}\right)=\sum_{k=1}^ig_k[k=i]\]

那么左边推右边的条件就是：

\[\sum_{j=k}^iB_{i,j}A_{j,k}=[k=i]\tag{2} \]

真正的反演原理：\((1)(2)\)两式同时成立，则有反演式\((0)\)成立.

对称矩阵的反演

\[f_i=\sum_{j=1}^iA_{i,j}g_j\Leftrightarrow g_i=\sum_{j=1}^iB_{i,j}f_j \\ \ \\ f_i=\sum_{j=i}^nA_{j,i}g_j\Leftrightarrow g_i=\sum_{j=i}^nB_{j,i}f_j\]

推导可知，上述两个反演式的代数充要条件均为：

\[\sum_{j=k}^iA_{i,j}B_{j,k}=[k=i]\land\sum_{j=k}^iA_{i,j}B_{j,k}=[k=i] \]

于是两个反演式等价.

反演系数转移

\[f_i=\sum_{j=1}^is_jA_{i,j}g_j\Leftrightarrow g_i=\sum_{j=1}^i B_{i,j} f_j \]

对于形如上式的带权反演，我们可以合并系数，将权值转移到右式.

\[f_i=\sum_{j=1}^iA_{i,j}G_j\Leftrightarrow \frac{G_i}{s_i}=\sum_{j=1}^i B_{i,j} f_j \\ \ \\ f_i=\sum_{j=1}^iA_{i,j}G_j\Leftrightarrow G_i=\sum_{j=1}^i s_iB_{i,j} f_j\]

常规等价反演

根据对称矩阵反演和反演系数转移，可以得知以下四种反演是等价的反演：

\[f_i=\sum_{j=1}^i(-1)^{j}A_{i,j}g_j\Leftrightarrow g_i=\sum_{j=1}^i (-1)^{j}B_{i,j} f_j \\ \ \\ f_i=\sum_{j=1}^iA_{i,j}g_j\Leftrightarrow g_i=\sum_{j=1}^i (-1)^{i+j}B_{i,j} f_j \\ \ \\ f_i=\sum_{j=i}^n(-1)^jA_{j,i}g_j\Leftrightarrow g_i=\sum_{j=i}^n(-1)^jB_{j,i}f_j \\ \ \\ f_i=\sum_{j=i}^nA_{j,i}g_j\Leftrightarrow g_i=\sum_{j=i}^n(-1)^{i+j}B_{j,i}f_j \]

• 当然反演可以是乘法形式的，仍然存在类似上式的等价形式.

容斥原理

补集转化

补集转化又称为减法原理，若集合\(S\)被划分成了两部分\(A,\overline{A}\)，则\(A\)对象的数目为\(|A|=|S|-|\overline{A}|\).

基本容斥原理

我们假设有全集\(S\)，以及\(n\)个集合，每个集合\(A_i\)中的元素具有性质\(P_i\).

现在我们要求不具有任何性质的集合大小，则有如下的计算公式：

\[\left |\bigcap_{i=1}^n\overline{A_i}\right|=|S|+\sum_{T\subseteq\{1,2,...,n\},T\not =\emptyset}(-1)^{|T|}\left | \bigcap_{i\in T}A_i \right | \]

移项一下就可以得到另一种等价形式：

\[\left | \bigcup_{i=1}^nA_i \right |=\sum_{T\subseteq \{1,2,...,n\}}(-1)^{|T|-1}\left | \bigcap_{i\in T} A_i \right | \]

两种形式的容斥原理都具有组合意义：

形式\(1\)：不具备任何性质的元素个数 \(=\) 元素总个数 \(-\) 至少具备一个性质的元素个数之和 \(+\) 至少具备两个性质的元素个数之和 \(-\) 至少具备三个性质的元素个数之和 \(...\)

形式\(2\)：所有集合的并集大小 \(=\) 所有集合的大小之和 \(-\) 每两个集合之间的交集大小 \(+\) 每三个集合之间的交集大小 \(...\)

以下提供一种形式\(2\)的证明：

考虑元素\(x\)被包含在\(k\)个集合中，则它在\(|T|=t，t \leq k\)的时候被计算了\(\binom{k}{t}\)次.

设其总共被计算了\(P\)次，构造\(f(x)=(1-x)^k\)，根据二项式定理展开得到：

\[f(x)=\sum_{i=0}^k\binom{k}{i}x^{k-i}(-1)^{i} \]

\[P=\binom{k}{1}-\binom{k}{2}+\binom{k}{3}-\cdots+(-1)^{k-1}\binom{k}{k} \]

观察发现\(f(1)=1-P\)，于是得出\(P=1\).

应用\(1\)：欧拉函数\(\varphi(n)\)的表达式为\(n\times\prod (1-\frac{1}{p_i})\).

证明：设\(S_i\)代表质因数\(p_i\)在\(1\sim n\)内所有倍数代表的集合，则\(\varphi(n)=n-\left | \bigcup _{i=1}^kS_i \right |\)，应用容斥原理，可得\(\varphi (n)=n-\sum_{T\subseteq P}(-1)^{|T|-1}\frac{n}{\prod_{i\in T}p_i}\)，提取\(n\)，因式分解即可.

应用\(2\)：错位排列\(D_n\)的通项公式为\(n!+\sum_{i=1}^n(-1)^{i}\binom{n}{i}(n-i)!\).

证明：令一个数字排在其原本的位置代表方案具有一个性质，套用容斥原理形式一即可.

应用\(3\)：第二类斯特林数\(\begin{Bmatrix}n\\m\end{Bmatrix}\)的表达式为\(\frac{1}{m!}\sum_{i=0}^{m}(-1)^i\tbinom{m}{i}(m-i)^n\).

证明：令一个盒子为空代表具有一个性质，套用容斥原理形式一，除掉盒子标号即可.

应用\(4\)：多重集组合数.

证明：公式在常见的组合问题一节中已经给出，把超额使用一类元素看组一个性质，用隔板法计算答案，套用容斥原理形式一即可.

广义容斥原理

设\(f\)，\(g\)为定义在指标集上的函数，则有如下等价关系：

\[f(S)=\sum_{T\subseteq S}g(T)\Leftrightarrow g(S)=\sum_{T\subseteq S}(-1)^{|S|-|T|}f(T) \]

证明：

首先右式代入左式，交换求和号：

\[f(S)=\sum_{P\subseteq S}f(P)\sum_{P\subseteq T\subseteq S}(-1)^{|T|-|P|} \\ \ \\ =\sum_{P\subseteq S}f(P)\sum_{i=0}^{|S|-|P|}(-1)^i\binom{|S|-|P|}{i} \\ \ \\ =\sum_{P\subseteq S}f(P)[|S|=|P|]=f(S)\]

最后一步使用了二项式定理的推论\(3\).

右式代入左式的证明过程相似，故定理成立.

快速Mobius变换

在广义容斥原理的式子中，我们可能需要求解一个数组的高位前缀和，也就是子集和，直接枚举子集是\(O(3^n)\)的，存在时间复杂度更低的算法.

我们可以考虑对一个集合\(S\)的子集贡献从高位到低位进行分类：首先是不包含最高位\(1\)子集的贡献，这其实是一个子问题；其次，包含最高位\(1\)的子集贡献我们再分为两类，不包含次高位\(1\)的子集贡献，这又是一个子问题；剩下同时包含最高位和次高位\(1\)的子集我们再类似地向下分类.

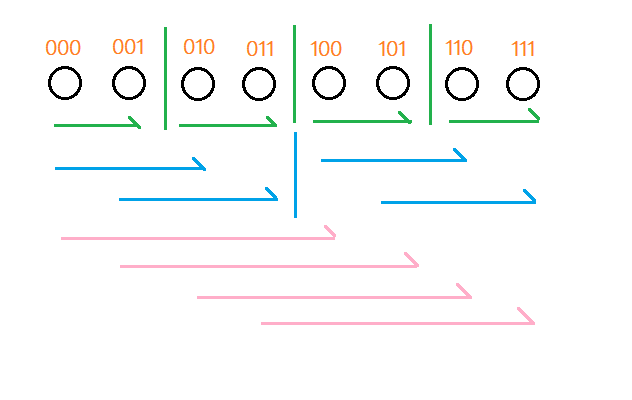
我们可以画出如上的贡献图. 以\(111\)为例，我们想知道它的子集和，首先可以考虑它的最高位\(1\)要不要，如果不要，那么可以直接把\(011\)的子集和累加给它，也就是最后一个粉丝箭头. 接着考虑要的情况，我们再看次高位的\(1\)要不要，如果不要，那么可以直接把\(101\)的子集和累加给它. 同样，最高两位都要的话，可以假设第三位不要，然后把\(110\)的子集和累加给它. 最后就是三位全都要了，显然他自己对自己也是有贡献的.

当然我们想要把\(011\)，\(101\)，\(110\)的子集和累加给\(111\)时，首先得保证它们的子集和已经求好了. 此时最好的方式就是直接按照图中箭头从上到下的顺序一层一层的枚举累加，这样就可以保证跨层询问子集和的时候一定已经完成累加了.

此时求和算法的时间复杂度类似于分治，有\(T(n)=2T(\frac{n}{2})+\frac{n}{2}\). 容易得知\(T(n)=O(n\log_2 n)\)，\(n=2^m\)时，时间复杂度就可以写成\(O(m\times 2^m)\)，\(m\)是元素个数.

还原算法我们称之为逆\(\mathrm{Mobius}\)变换，只需把贡献扣掉就好了.

// t = 1 --> FMT , t = -1 --> IFMT
inline void FMT(int *a, int n, int t) 
{
    for (int i = 1; i < 1 << n; i <<= 1) 
    // i : the length of contribution arrow 
        for (int p = i << 1 , j = 0; j < 1 << n; j += p) 
        // p : the length of section , j : the number of position
            for (int k = 0; k < i; k++) a[i+j+k] += t * a[j+k];
            // k : go through the section and add contribution 
}

二项式反演

令\(f(S)=F(|S|)\)，\(g(S)=G(|S|)\)，套用广义容斥原理：

\[F(|S|)=\sum_{T\subseteq S}G(|S|)\Leftrightarrow G(|S|)=\sum_{T\subseteq S}(-1)^{|S|-|T|}F(|T|) \\ \ \\ F(|S|)=\sum_{i=0}^{|S|}\binom{|S|}{i}G(i)\Leftrightarrow G(|S|)=\sum_{i=0}^{|S|}(-1)^{|S|-i}\binom{|S|}{i}F(i)\]

可以把\(|S|\)，\(|T|\)直接看成整数，得到：

\[f(x)=\sum_{i=0}^{x}{x \choose i}g(i)\Leftrightarrow g(x)=\sum_{i=0}^{x}(-1)^{x-i}\binom{x}{i}f(i)\]

我们称这个反演式为二项式反演.

根据反演原理，我们还可以得到另外三种等价形式，其中最常用的是这种：

\[f(x)=\sum_{i=x}^{n}\binom{i}{x}g(i)\Leftrightarrow g(x)=\sum_{i=x}^{n}(-1)^{x-i}\binom{i}{x}f(i)\]

二项式反演的重要运用是至少和恰好型方案数的转换.

首先，我们设\(\alpha(k)\)代表所有至少满足\(k\)的性质的方案数之和.

\[\alpha(k)=\sum_{T\subseteq\{1,2,...,n\},|T|=k}\left | \bigcap_{i\in T}A_i \right | \]

我们发现\(\alpha(k)\)将具有\(p(p\geq k)\)个性质的元素计算了\(\binom{p}{k}\)次.

假设\(\beta(k)\)代表恰好具有\(k\)个元素的方案数，则有递推公式如下：

\[\beta(k)=\alpha(k)-\sum_{i=k+1}^n\binom{i}{k}\beta(i) \\ \ \\ \alpha(k)=\sum_{i=k}^n\binom{i}{k}\beta(i)\]

二项式反演，可以得到\(\beta(k)\)的计算式：

\[\beta(k)=\sum_{i=k}^n(-1)^{i-k}\binom{i}{k}\alpha(i) \]

应用\(1\)：推导错位排列\(D_n\)的通项公式.

设\(f_i\)代表恰好\(i\)个位置错排的方案数，则可以进行二项式反演：

\[n!=\sum_{i=0}^n\binom{n}{i}f_i \]

应用\(2\)：推导第二类斯特林数\(\begin{Bmatrix}n\\m\end{Bmatrix}\)的表达式

假设盒子有标号，设\(f_i\)代表恰好\(i\)个盒子非空的方案数，则可以二项式反演，答案除掉盒子标号即可：

\[m^n=\sum_{i=0}^m\binom{m}{i}f_i \]

应用\(3\)：球染色问题：有\(n\)个球排成一行，你有\(k\)种颜色，要求给每一个球染色，相邻两个球颜色不可以相同，并且每种颜色至少使用一次，求方案数.

假设\(f_i\)代表恰好使用\(i\)种颜色的方案数，则可以二项式反演：

\[k(k-1)^{n-1}=\sum_{i=0}^{k}{k \choose i}f_i \]

Min-Max容斥

首先我们把一个整数\(n\)看成一个集合\(S(n)=\{1,2,\cdots,n\}\)，那么：

\[\min_{i=1}^n\{a_i\}=\left| \bigcap_{i=1}^nS(a_i) \right|\ ,\ \max_{i=1}^n\{a_i\}=\left| \bigcup_{i=1}^nS(a_i) \right| \]

可以用容斥原理改写\(\max\)的表达式：

\[\max_{i=1}^n\{a_i\}=\left|\bigcup_{i=1}^nS(a_i)\right| =\sum_{T\subseteq \{1,2,\cdots ,n\}}(-1)^{|T|-1}\left| \bigcap_{i\in T} S(a_i) \right|\]

于是就可以得到：

\[\max_{i=1}^n\{a_i\}=\sum_{T\subseteq \{1,2,\cdots ,n\}}(-1)^{|T|-1}\min_{i\in T}\{a_i\} \]

把\(\min\max\)反过来该式也成立，在期望意义下该式也成立.

Kth Min-Max容斥

我们可以套用一般\(\min-\max\)容斥的式子猜想一个\(k\)大值容斥的形式：

\[\mathrm{Kth}\max_{i=1}^n\{a_i\}=\sum_{T\subseteq \{1,2,\cdots,n\}}f(|T|)\min_{i\in T}\{a_i\} \]

其中\(f(|T|)\)是容斥系数，具体是多少还不知道.

第\(x+1\)大的元素显然会被统计到\(\sum_{i=0} ^x {x\choose i} f(i+1)\)次，我们可以直接令\([x+1=k]=\sum_{i=1}^x {x \choose i}f(i+1)\)，于是就可以二项式反演，得到：

\[f(x+1)=\sum_{i=0}^x (-1)^{x-i} {x \choose i}[i+1=k] \]

化简得到容斥系数\(f(x)=(-1)^{x-k}{x-1 \choose k-1}\).

高维Min-Max容斥

定义多元组的\(\min\)算符为：\(\min((x_1,x_2,\cdots,x_n),(y_1,y_2,\cdots,y_n))=(\min(x_1,y_1),\min(x_2,y_2),\cdots,\min(x_n,y_n))\).

可以证明，原来的\(\min-\max\)容斥在高维情况下也成立.

设\(n=\prod_{i=1}^kp_i^{a_i}\)，每个正整数的代表元素组为\((a_1,a_2,\cdots,a_k)\)，那么该意义下的高维\(\min-\max\)容斥就等价于：

\[\mathrm{gcd}_{i=1}^n\{a_i\}=\prod_{T\subseteq \{1,2,\cdots ,n\}}\mathrm{lcm}_{i\in T}^{(-1)^{|T|-1}}\{a_i\} \]

Epilogue

第一篇总结现已施工完毕，如有错误请提出.