『Border Series在回文自动机上的运用』

符号

• \(s[l:r]\)表示字符串\(s\)下标在\(l,r\)间的子串。
• \(s^R\)表示字符串\(s\)的反转。
• \(\mathrm{AB}\)表示字符串\(\mathrm{A}\)和字符串\(\mathrm{B}\)的拼接。
• \(\mathrm{A}^k\)表示字符串\(\mathrm{A}\)自我拼接\(k\)次。
• 为了表述方便，有时回文自动机的节点也直接表示该节点代表的字符串。

Border Series

首先我们要知道\(\mathrm{Border}\)是一个字符串的公共前后缀，并且我们将前缀函数\(\pi(p)\)定义为字符串\(s\)的前缀\(p\)的最长\(\mathrm{Border}\)长度。

那么，容易得知一个长度为\(n\)的字符串\(s\)所有\(\mathrm{Border}\)的集合可以表示为$$\mathrm{T}={s[1:\pi(n)],s[1:\pi(\pi(n))],s[1:\pi(\pi(\pi(n)))],...}$$

也就是说\(\mathrm{Border}\)的\(\mathrm{Border}\)还是你的\(\mathrm{Border}\)，然后我们来讲点有用的。

\(\mathrm{Lemma1:}\) 字符串\(t\)是回文串\(s\)的一个回文后缀，当且仅当\(t\)是\(s\)的\(\mathrm{Border}\)。

不难理解，因为回文串的定义就是\(p^R=p\)的字符串，由于\(s\)回文，所以\(s[1,|t|]=t^R\)，又因为\(t\)回文，所以\(t^R=t\)，也就是说\(s\)有一个长度为\(|t|\)的\(\mathrm{Border}\)。

我们现在要考虑这个引理的逆命题是否成立：字符串\(s\)存在\(\mathrm{Border}\) \(t\)回文，那么是否可以推出\(s\)回文？

显然是不成立的，因为我们没有充分得知\(s[|t|+1,n-|t|]\)这个子串回文，所以也不能推出\(s\)回文。

不过没关系，我们只要满足\(|t|\geq\frac{|s|}{2}\)就好了，这样子串\(s[|t|+1,n-|t|]\)就不存在。

\(\mathrm{Lemma2:}\) 字符串\(s\)存在\(\mathrm{Border}\) \(t\)回文，且\(|t|\geq\frac{|s|}{2}\)，则\(s\)回文。

现在，我们要讲讲回文自动机了。我们知道，回文自动机上的每个节点\(p\)都有一个后缀链接\(\mathrm{link}(p)\)，指向其最长回文后缀所对应的节点。定义\(\mathrm{dif}(x)=\mathrm{len}(x)-\mathrm{len}(\mathrm{link}(x))\)，\(\mathrm{slink}(x)\)为\(x\)后缀链接路径上第一个\(\mathrm{dif}(x)\not=\mathrm{dif}(\mathrm{link}(x))\)的祖先。

\(\mathrm{Corollary1:}\) 回文自动机上的节点\(x\)，沿着\(\mathrm{link}\)向上跳到根，经过的节点数为\(O(n)\)，沿着\(\mathrm{slink}\)向上跳到根，经过的节点数为\(O(\log_2 n)\)。

\(\mathrm{Proof.}\)

\(\mathrm{Case1:}\) \(\mathrm{dif}(x)> \frac{\mathrm{len}(x)}{2}\)，此时有\(\mathrm{slink}(x)=\mathrm{link}(x)\)，但是每跳一次字符串长度至少减小一半，所以这样的跳跃次数是\(O(\log_2n)\)的。

\(\mathrm{Case2:}\) \(\mathrm{dif}(x)\leq \frac{\mathrm{len}(x)}{2}\)，此时\(x\)的有一个长于一半的最长回文后缀。

根据\(\mathrm{Lemma1}\)，\(\mathrm{link}(x)\)是\(x\)的最长\(\mathrm{Border}\)，且长于\(x\)的一半。我们知道，如果字符串\(t\)是\(s\)的\(\mathrm{Border}\)，则\(s[1:n-|t|]\)是\(s\)的循环节。所以我们就可以用循环节把\(x\)表示为\(\mathrm{D}^k\mathrm{T}\)的形式，其中\(\mathrm{T}\)是\(\mathrm{D}\)的前缀，\(k\geq 2\)。

由于\(\mathrm{D}^k\mathrm{T}\)是\(x\)最长\(\mathrm{Border}\)的循环表示，所以\(x\)的最长\(\mathrm{Border}\)就是\(\mathrm{D}^{k-1}\mathrm{T}\)。根据\(\mathrm{Lemma1}\)，\(\mathrm{D}^{k-1}\mathrm{T}\)回文，所以\(\mathrm{link}(x)\)就是\(\mathrm{D}^{k-1}\mathrm{T}\)。

以此类推，可知\(\mathrm{slink}(x)\)就是\(\mathrm{T}\)，又因为\(\mathrm{dif}(x)\leq \frac{\mathrm{len}(x)}{2}\)，所以\(|\mathrm{T}|<\mathrm{dif}(x)\leq \frac{\mathrm{len}(x)}{2}\)。字符串长度也是至少减小一半的，所以这样的跳跃次数是\(O(\log_2n)\)的。

综上，\(\mathrm{slink}\)链的长度是\(O(\log_2n)\)级别的。

换一种说法，\(\mathrm{Corollary1}\)等价于一个字符串\(s\)所有回文后缀的长度构成的序列可以划分为不超过\(\log_2|s|\)个等差数列。那么等差数列的信息，我们就可以想办法维护了。

例题

SPOJ IITKWPCE

题目大意：给定一个长度为\(n\)的字符串，要求将其划分为数量最少的子串，使得每个子串都是一个回文串。

\(n\leq 2000,T\leq 100\)

Solution

\(\mathrm{Border\ Series}\)最经典的应用就是回文串划分的\(\mathrm{dp}\)。

设\(f(i)\)为前缀\(s[1:i]\)的最少划分数，可以列出\(\mathrm{dp}\)方程：

\[f(i)=\min_{j<i,s[j+1:i]\in \mathrm{Palindromes}}\{f(j)+1\} \]

对于每一个\(i\)，如果在回文树上遍历所有右端点为\(i\)的回文串的话时间复杂度就是\(O(n^2)\)的，毫无意义。

我们可以利用\(\mathrm{Border\ Series}\)的等差性质，建立一个辅助数组\(g\)来算\(\mathrm{dp}\)值。

\[g(x)=\min_{\mathrm{link}(t)=\mathrm{slink}(x)}\{f(\mathrm{pos}(x)-\mathrm{len}(x)),f(\mathrm{pos}(\mathrm{link}(x))-\mathrm{len}(\mathrm{link}(x))),\cdots,f(\mathrm{pos}(t)-\mathrm{len}(t))\} \]

其中\(x\)就是回文树上的一个节点，\(\mathrm{pos}(x)\)就是该节点回文串最后一次出现的右端点位置。

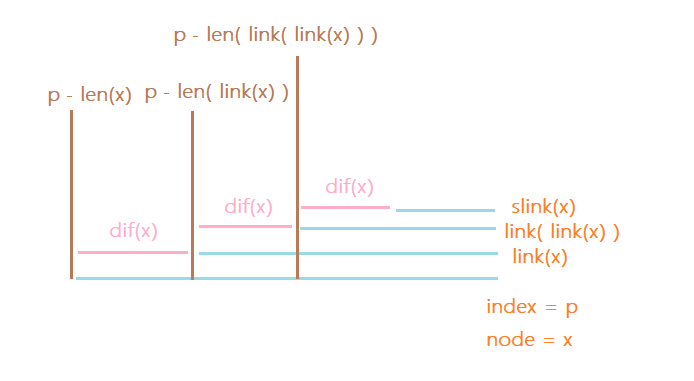
如图，假设当前\(\mathrm{dp}\)到了\(p\)位置，在回文自动机上节点为\(x\)，那么\(g(x)\)就应该对应了这三条棕线位置的\(\mathrm{dp}\)值取\(\min\)。

也就是说，我们可以把节点\(x\)到根的\(\mathrm{link}\)路径根据\(\mathrm{slink}\)划分为\(\log\)条链，每个\(\mathrm{slink}\)作为一条链的开头。现在，\(g(x)\)就是节点\(x\)到其所在链的链头所有回文串应该取的\(\mathrm{dp}\)值取\(\min\)。

那么，对于\(f(p)\)来说，我们只需要对其到根的\(\mathrm{slink}\)路径上所有\(g(x)+1\)取\(\min\)即可。这样对\(f\)进行状态转移的时间复杂度就优化到了\(O(\log_2n)\)。

那\(g\)数组如何维护呢？且慢，我们先来看看为什么要这样划分。

\(\mathrm{Corollary2:}\) 一条\(\mathrm{slink}\)链上非链底的所有节点，若最后一次出现位置为\(p\)，则倒数第二次出现位置为\(p-\mathrm{dif(x)}\)。

\(\mathrm{Proof.}\)

首先，\(x\)可以是这条链上的任何一个节点，因为整条链的\(\mathrm{dif}\)值应该都是相同的。

如图，我们要证明除了底端的那条蓝线以外，所有蓝线代表回文串的上一次出现位置就是其下方的绿线位置，下面以\(x\)和\(\mathrm{link}(x)\)为例。

根据\(\mathrm{Pemma1}\)，每个\(\mathrm{link}(x)\)都是\(x\)的\(\mathrm{Border}\)，所以绿线位置肯定是它的一个出现位置，只需证明区间\([p-\mathrm{dif}(x)+1,p-1]\)它不可能在出现即可。

反证法，假设其在区间\([p-\mathrm{dif}(x)+1,p-1]\)中又出现过了，位置为\(t\)，根据\(\mathrm{Pemma2}\)，则字符串\(s[t-\mathrm{len}(\mathrm{link(x)})+1:p]\)回文，显然其长度大于\(\mathrm{len}(\mathrm{link}(x))\)，与\(x\)的最长回文后缀是\(\mathrm{link}(x)\)矛盾。

当然，对于\(\mathrm{slink}(x)\)这个串来说，它的长度小于其儿子的一半，此时\(\mathrm{Pemma2}\)不成立，证明失效，所以我们把他划分到另一个链的链底。

这有什么用呢？我们直接看证明的那幅图，\(g(x)\)就是除最顶端\(\mathrm{slink}(x)\)外所有蓝线最左端那个点的\(\mathrm{dp}\)值取\(\min\)。根据\(\mathrm{Corollary2}\)，\(\mathrm{link}(x)\)上一次出现在\(p-\mathrm{dif}(x)\)，也就是最下绿线位置，我们发现\(g(\mathrm{link}(x))\)就是所有绿线最左端那个点的\(\mathrm{dp}\)值取\(\min\)。

也就是说，\(g(x)\)和\(g(\mathrm{link}(x))\)具有极高的相似度，\(g(x)\)可以从\(g(\mathrm{link}(x))\) \(O(1)\)转移而来。

\[g(x)=\min\{g(\mathrm{link}(x)),f(p-\mathrm{len}(\mathrm{slink}(x))-\mathrm{dif}(x))\} \]

那么问题迎刃而解，只需\(O(\log_2n)\)转移\(f\)的同时\(O(1)\)维护一下\(g\)即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 2020;
struct PalindromesAutomaton
{
    int tot,last,n,link[N],len[N],trans[N][26],slink[N],dif[N],s[N];
    inline void Init(void)
    {
        memset( trans , 0 , sizeof trans );
        memset( len , 0 , sizeof len );
        memset( link , 0 , sizeof link );
        len[ last = 0 ] = 0 , link[0] = 1;
        s[ n = 0 ] = len[1] = -1 , tot = 1;
    }
    inline void Extend(int c)
    {
        int p = last; s[++n] = c;
        while ( s[n] != s[ n - len[p] - 1 ] ) p = link[p];
        if ( trans[p][c] == 0 )
        {
            int cur = ++tot , q = link[p];
            len[cur] = len[p] + 2;
            while ( s[n] != s[ n - len[q] - 1 ] ) q = link[q];
            link[cur] = trans[q][c] , trans[p][c] = cur;
            dif[cur] = len[cur] - len[ link[cur] ];
            if ( dif[cur] != dif[ link[cur] ] ) slink[cur] = link[cur];
            else slink[cur] = slink[ link[cur] ];
        }
        last = trans[p][c];
    }
};
PalindromesAutomaton T;
int Case,n,f[N],g[N]; char s[N];
int main(void)
{
    scanf( "%d" , &Case );
    while ( Case --> 0 )
    {
        scanf( "%s" , s+1 );
        T.Init() , n = strlen( s + 1 );
        memset( f , 0x3f , sizeof f );
        memset( g , 0x3f , sizeof g );
        f[0] = 0;
        for (int i = 1; i <= n; i++)
        {
            T.Extend( s[i] - 'a' );
            for (int j = T.last; j; j = T.slink[j])
            {
                g[j] = f[ i - T.len[T.slink[j]] - T.dif[j] ];
                if ( T.slink[j] ^ T.link[j] ) g[j] = min( g[j] , g[T.link[j]] );
                f[i] = min( f[i] , g[j] + 1 );
            }
        }
        printf( "%d\n" , f[n] );
    }
    return 0;
}

BZOJ5384

给定一个长度为\(n\)的字符串，有\(Q\)次询问，每次询问给定一个区间，询问区间内有多少个本质不同的回文子串。

\(n\leq 3\times10^5,Q\leq 10^6\)

Solution

首先考虑暴力，按照树状数组区间数颜色的思路，我们把询问离线，然后右端点增量构建回文自动机，并用树状数组记录每个回文串最后一次出现的位置的左端点，于是询问就是树状数组区间查询。

那么我们考虑好怎么处理加一个右端点时出现的那些回文串即可。显然，在回文自动机上，这些回文串就是\(\mathrm{link}\)树上一条到根的链，我们遍历这条链，在上一次出现位置的左端点取消贡献，这一次出现位置的左端点加上贡献即可。

如何查询上一次出现的位置？可以在回文自动机的节点上记录一下最后一次出现的位置，那么问题转化为子树求\(\max\)，用线段树维护。

这样的话，时间复杂度就是\(O(n^2\log_2n)\)。

根据上题的经验，我们自然想到把遍历回文后缀树上一条到根的链这一操作从\(\mathrm{slink}\)划分的角度来考虑。

根据\(\mathrm{Corollary2}\)，我们发现一条\(\mathrm{slink}\)链上非底端的串上一次出现位置的左端点就是它儿子这一次出现位置的左端点，于是贡献相抵消。只需在最底端串上一次出现位置的左端点贡献减一，最顶端串这一次出现位置的左端点加一即可，时间复杂度优化到\(O(n\log^2n)\)。

由于\(\mathrm{BZOJ}\)爆炸了没法评测，代码就不放了。