『保卫王国 树上倍增dp』
<更新提示>
<正文>
保卫王国
Description
Z 国有n座城市,n - 1条双向道路,每条双向道路连接两座城市,且任意两座城市 都能通过若干条道路相互到达。
Z 国的国防部长小 Z 要在城市中驻扎军队。驻扎军队需要满足如下几个条件:
一座城市可以驻扎一支军队,也可以不驻扎军队。
由道路直接连接的两座城市中至少要有一座城市驻扎军队。
在城市里驻扎军队会产生花费,在编号为i的城市中驻扎军队的花费是pipi。
小 Z 很快就规划出了一种驻扎军队的方案,使总花费最小。但是国王又给小 Z 提出 了m个要求,每个要求规定了其中两座城市是否驻扎军队。小 Z 需要针对每个要求逐一 给出回答。具体而言,如果国王提出的第j个要求能够满足上述驻扎条件(不需要考虑 第 j 个要求之外的其它要求),则需要给出在此要求前提下驻扎军队的最小开销。如果 国王提出的第j个要求无法满足,则需要输出-1 (1 ≤ j ≤ m)。现在请你来帮助小 Z。
Input Format
第 1 行包含两个正整数n,m和一个字符串type,分别表示城市数、要求数和数据类型。type是一个由大写字母 A,B 或 C 和一个数字 1,2,3 组成的字符串。它可以帮助你获得部分分。你可能不需要用到这个参数。这个参数的含义在【数据规模与约定】中 有具体的描述。
第 2 行n个整数,pipi表示编号i的城市中驻扎军队的花费。
接下来 n - 1 行,每行两个正整数u,v,表示有一条u到v的双向道路。
接下来 m 行,第j行四个整数a,x,b,y(a ≠ b),表示第j个要求是在城市a驻扎x支军队, 在城市b驻扎y支军队。其中,x 、 y 的取值只有 0 或 1:若 x 为 0,表示城市 a 不得驻 扎军队,若 x 为 1,表示城市 a 必须驻扎军队;若y为 0,表示城市 b不得驻扎军队, 若y为 1,表示城市 b 必须驻扎军队。
输入文件中每一行相邻的两个数据之间均用一个空格分隔。
Output Format
输出共 m 行,每行包含 1 个整数,第j行表示在满足国王第j个要求时的最小开销, 如果无法满足国王的第j个要求,则该行输出−1。
Sample Input
5 3 C3
2 4 1 3 9
1 5
5 2
5 3
3 4
1 0 3 0
2 1 3 1
1 0 5 0
Sample Output
12
7
-1
解析
如果不考虑特殊限制的话,就是一个最小权覆盖集问题,显然可以用树形\(dp\)做。
对于每一次限制都重做一遍\(dp\)显然是不行的,我们就要考虑怎样在预处理一些\(dp\)值的情况下快速求出被限制后的答案。没有任何限制的\(dp\)直接用"没有上司的舞会"一题的树上\(dp\)解法就可以了。
那么我们就需要考虑一次点对的限制会影响哪一些\(dp\)值,可以看下图:
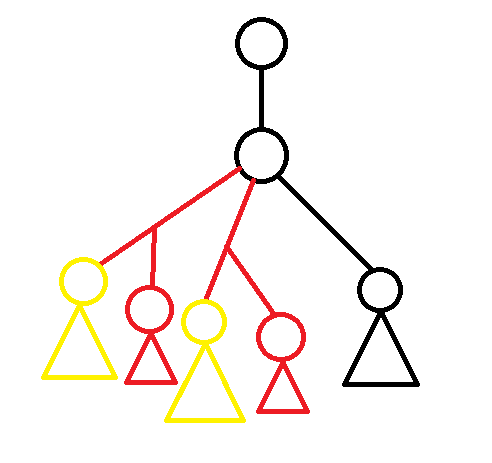
我们可以把限制后的树分为三部分,分别是图中的黑色,红色,黄色。黄色部分就是限制的两个点及其子树,红色的部分就是限制的两个点分别到其\(lca\)的路径和路径上的其它子树,黑色部分就是整棵树除了两个限制点\(lca\)的子树以为的部分。
我们发现黄色部分和黑色部分的\(dp\)值都是可以预处理的:
设\(f[x][0/1]\)代表以\(x\)为根的子树中,不取/取\(x\)这个点的最小权覆盖集
\[f[x][0]=\sum_{y\in son(x)} f[y][1]\\f[x][1]=\sum_{y\in son(x)}min(f[y][0],f[y][1]) \]设\(g[x][0/1]\)代表除了以\(x\)为根的子树中,不取/取\(x\)这个点的最小权覆盖集
\[\forall y\in son(x)\ ,\ g[y][0]=g[x][1]+f[x][1]-min(f[y][0],f[y][1])\\ \forall y\in son(x)\ ,\ g[y][1]=min(g[y][0],g[x][0]+f[x][0]-f[y][1]) \]
好了,接下来就考虑红色部分怎么算了。处理树上点对到\(lca\)的路径问题,容易想到倍增求\(lca\)的遍历方式,又因为要处理路径上其他子树的\(dp\)值,所以我们可以设置一个如下的\(dp\)状态:
设\(x\)的\(2^k\)倍祖先的\(p\),则\(F[x][k][0/1][0/1]\)代表\(x\)取/不取,\(p\)取/不取,\(p\)的子树减去\(x\)的子树这一部分的最小权覆盖集。
这是一个倍增的状态,于是就会有两个问题:如何预处理?如何拼接答案?
预处理的方式和普通的树上倍增差不多,重点看一下怎样倍增得到答案:
\(1.\) 对于深度大一点的节点\(x\),我们先把它跳到深度和\(y\)一样大的位置,并在倍增的过程中每次枚举两个端点取或不取的状态,用最小的花费转移即可,记录下答案。
\(2.\) 用同样的方式将\(x\),\(y\)两个点都向上跳,累加答案。
\(3.\) 最后汇合到\(lca\)的两个儿子时,根据\(lca\)取或不取来讨论,得到两种答案,取最小值作为本次询问的答案。
其实,这道题本质上就是结合了树形\(dp\)和树上倍增两种算法,只要能够深入理解状态,就可以很快的想到倍增的方法。
\(Code:\)
#include<bits/stdc++.h>
using namespace std;
const int N = 100020 , M = 100020 , MaxlogN = 30;
const long long INF = 1LL<<60;
struct edge{int ver,next;}e[N*2];
int n,m,t,Head[N*2],val[N]; char op[10];
int dep[N],fa[N][MaxlogN+2];
long long f[N][2],g[N][2];
long long F[N][MaxlogN][2][2];
inline int read(void)
{
int x = 0 , w = 0; char ch = ' ';
while ( !isdigit(ch) ) w |= ch=='-' , ch = getchar();
while ( isdigit(ch) ) x = x*10 + ch-48 , ch = getchar();
return w ? -x : x;
}
inline void insert(int x,int y)
{
e[++t] = (edge){y,Head[x]} , Head[x] = t;
e[++t] = (edge){x,Head[y]} , Head[y] = t;
}
inline void input(void)
{
n = read() , m = read();
scanf("%s",op);
for (int i=1;i<=n;i++)
val[i] = read();
for (int i=1;i<n;i++)
insert( read() , read() );
}
// 先dfs求fa和dep,顺带求原始的dp数组f:子树x的最小权覆盖集
inline void dfs(int x,int Fa)
{
dep[x] = dep[Fa] + 1 , fa[x][0] = Fa;
f[x][1] = val[x];
for (int i=Head[x];i;i=e[i].next)
{
int y = e[i].ver;
if ( y == Fa ) continue;
dfs( y , x );
f[x][0] += f[y][1];
f[x][1] += min( f[y][0] , f[y][1] );
}
}
// 树形dp求g数组:子树x的补集的 最小权覆盖集
inline void dp(int x,int Fa)
{
for (int i=Head[x];i;i=e[i].next)
{
int y = e[i].ver;
if ( y == Fa ) continue;
g[y][0] = g[x][1] + f[x][1] - min( f[y][0] , f[y][1] );
g[y][1] = min( g[y][0] , g[x][0] + f[x][0] - f[y][1] );
dp( y , x );
}
}
// 利用f数组计算倍增数组
inline void prework(void)
{
memset( F , 0x3f , sizeof F );
for (int i=1;i<=n;i++)
{
int Fa = fa[i][0];
F[i][0][0][0] = INF;
F[i][0][0][1] = f[Fa][1] - min( f[i][0] , f[i][1] );
F[i][0][1][0] = f[Fa][0] - f[i][1];
F[i][0][1][1] = f[Fa][1] - min( f[i][0] , f[i][1] );
}
for (int k=1;k<=25;k++)
{
for (int i=1;i<=n;i++)
{
int Fa = fa[i][k-1];
if ( !fa[Fa][k-1] ) continue;
fa[i][k] = fa[Fa][k-1];
for (int u=0;u<=1;u++)
for (int v=0;v<=1;v++)
for (int w=0;w<=1;w++)
F[i][k][u][v] = min( F[i][k][u][v] , F[i][k-1][u][w] + F[Fa][k-1][w][v] );
}
}
}
// 树上倍增拼接答案
inline long long solve(int x,int a,int y,int b)
{
if ( dep[x] < dep[y] )
swap( x , y ) , swap( a , b );
long long tx[2] = {INF,INF} , ty[2] = {INF,INF};
long long nx[2],ny[2];
tx[a] = f[x][a] , ty[b] = f[y][b];
for (int i=25;i>=0;i--)
{
if ( dep[fa[x][i]] < dep[y] ) continue;
nx[0] = nx[1] = INF;
for (int u=0;u<=1;u++)
for (int v=0;v<=1;v++)
nx[u] = min( nx[u] , tx[v] + F[x][i][v][u] );
tx[0] = nx[0] , tx[1] = nx[1];
x = fa[x][i];
}
if ( x == y ) return nx[b] + g[y][b];
for (int i=25;i>=0;i--)
{
if ( fa[x][i] == fa[y][i] ) continue;
nx[0] = nx[1] = ny[0] = ny[1] = INF;
for (int u=0;u<=1;u++)
for (int v=0;v<=1;v++)
nx[u] = min( nx[u] , tx[v] + F[x][i][v][u] ),
ny[u] = min( ny[u] , ty[v] + F[y][i][v][u] );
tx[0] = nx[0] , tx[1] = nx[1];
ty[0] = ny[0] , ty[1] = ny[1];
x = fa[x][i] , y = fa[y][i];
}
int p = fa[x][0];
long long res1 = f[p][0] - f[x][1] - f[y][1] + tx[1] + ty[1] + g[p][0];
long long res2 = f[p][1] - min( f[x][0] , f[x][1] ) - min( f[y][0] , f[y][1] )
+ min( tx[0] , tx[1] ) + min( ty[0] , ty[1] ) + g[p][1];
return min( res1 , res2 );
}
int main(void)
{
input();
dfs( 1 , 0 );
dp( 1 , 0 );
prework();
for (int i=1;i<=m;i++)
{
int x = read() , a = read() , y = read() , b = read();
if ( a == 0 && b == 0 && ( fa[x][0] == y || fa[y][0] == x ) )
puts("-1");
else printf("%lld\n",solve(x,a,y,b));
}
return 0;
}
<后记>


 浙公网安备 33010602011771号
浙公网安备 33010602011771号