『Blocks 区间dp』

<更新提示>

<第一次更新>

<正文>

Blocks#

Description#

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold. The corresponding picture will be as shown below:

If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get kk points. for example, if you click on a silver box, the silver segment disappears, you got 44=16 points.

Now let's look at the picture below:

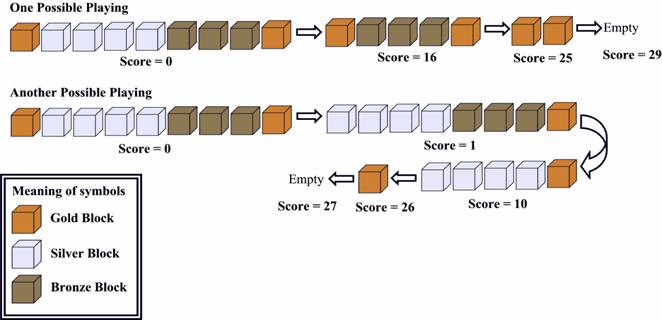
The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

题意：通过点击某一颜色消除相邻的所有的这种颜色，得分为len*len,求最大分

Input Format#

第一行为一个整数 N。

第二行为 A1,A2,…,AN。

Output Format#

一行一个整数，代表最大价值。

Sample Input#

Copy
9
1 2 2 2 2 3 3 3 1

Sample Output#

Copy
29

解析#

这种区间操作类的最优解问题显然是区间 $dp$ ，不过这道题的状态有点棘手。

对于一次消除操作，可能会带来左右两边原本不相邻的部分合并带来的影响，所以通常来说的状态是不行了。我们考虑设计一种状态能够记录这种合并带来的影响：设 $f[l][r][k]$ 代表区间消除 $[l,r]$ ，序列后面通过消除操作使得有 $k$ 个颜色为 $a[r]$ 的块跟在区间 $[l,r]$ 后面的最大得分。

考虑转移，显然，我们可以直接将后面跟着的 $k$ 个块和第 $r$ 个块连在一起消掉，这是一种转移方式。还有就是我们可以在区间 $[l,r-1]$ 中枚举一个颜色与 $a[r]$ 相同的点 $i$ ，然后将区间 $[i+1,r-1]$ 作为一个子问题直接消去，这样就使得 $a[r]$ 加入后面跟着的 $k$ 个块中， $i$ 成为右端点，利用这个状态转移即可。

至于如何枚举区间内和 $a[r]$ 颜色相同的点呢？这是可以预处理直接向前查找的。

$Code:$

Copy
#include<bits/stdc++.h>
using namespace std;
const int N = 220;
int n,a[N],pre[N],last[N];
int f[N][N][N];
inline void input(void)
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
        scanf("%d",&a[i]);
}
inline void init(void)
{
    for (int i=1;i<=n;i++)
    {
        pre[i] = last[a[i]];
        last[a[i]] = i;
    }
}
inline int dp(int l,int r,int k)
{
    if ( l > r ) return 0;
    if ( f[l][r][k] ) return f[l][r][k];
    f[l][r][k] = dp( l , r-1 , 0 ) + (k+1) * (k+1);
    for (int i=pre[r];i>=l;i=pre[i])
        f[l][r][k] = max( f[l][r][k] , dp( l , i , k+1 ) + dp( i+1 , r-1 , 0 ) );
    return f[l][r][k];
}
int main(void)
{
    input();
    init();
    memset( f , 0 , sizeof f );
    dp( 1 , n , 0 );
    printf("%d\n",f[1][n][0]);
    return 0;
}