『线段树及扫描线算法 Atlantis』
<更新提示>
入门看这边『线段树 Segment Tree』。
<第一次更新>
<正文>
扫描线
扫描线是一种解决一类平面内统计问题的算法，通常会借助线段树来实现，我们通过一道例题来引入这个算法。
Atlantis
Description
There are several ancient Greek texts that contain descriptions of the fabled island Atlantis.
Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist.
You (unwisely) volunteered to write a program that calculates this quantity.
Input Format
The input consists of several test cases. Each test case starts with a line containing a single integer n (1 <= n <= 100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0 <= x1 < x2 <= 100000;0 <= y1 < y2 <= 100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area. The input file is terminated by a line containing a single 0. Don't process it.
Output Format
For each test case, your program should output one section. The first line of each section must be "Test case #k", where k is the number of the test case (starting with 1). The second one must be "Total explored area: a", where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point. Output a blank line after each test case.
Sample Input
2
10 10 20 20
15 15 25 25.5
0
Sample Output
Test case #1
Total explored area: 180.00
解析
题目大意：给定平面内的\(n\)个矩形，求这\(n\)个矩形的面积并。
这是扫描线算法的引入问题，我们尝试设想有一条无限高的竖线左往右扫过这个并集图形，按照每一个矩形的的左右边界，我们可以将这个并集图形分为\(2n\)段，对于两两相邻的部分，我们可以分别计算面积，这样就得到了整个并集图形的面积。
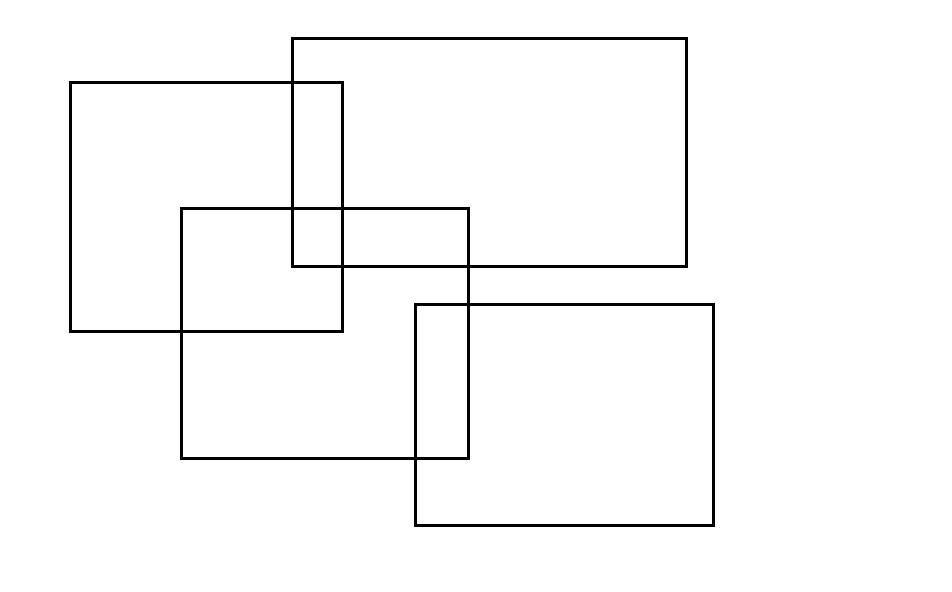
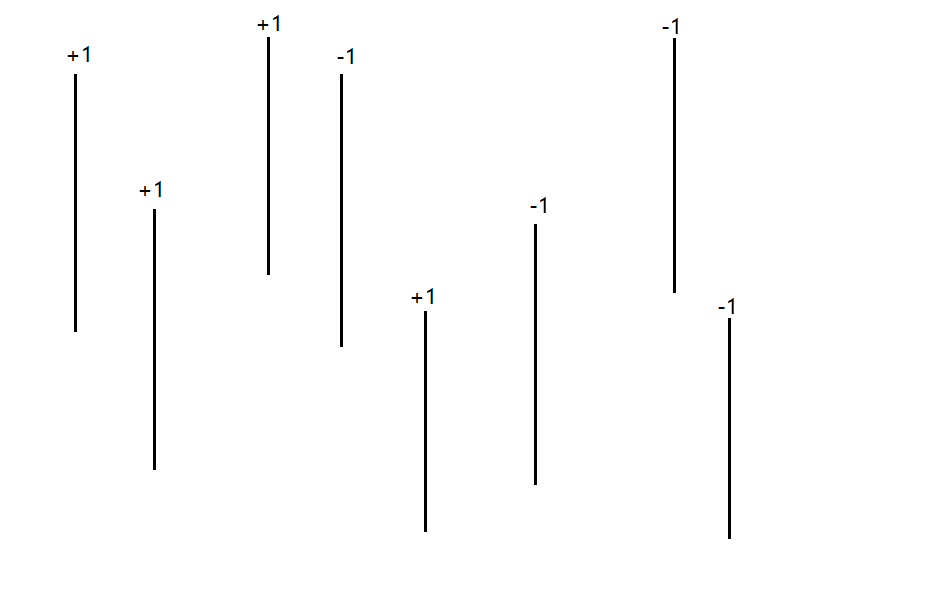
如图，我们就是把每个矩形的左右边界提了出来，就变成了这样一些线段。
那么我们需要这些量化记录下来：每个四元组\((x,y_1,y_2,1/-1)\)分别代表了一条线段，\(x\)是线段的横坐标，\((y_1,y_2)\)是线段上下端点的纵坐标，\(1/-1\)代表了这条线段是矩形的左边界还是右边界。
显然，我们只需要把这些线段按照横坐标排序，对于一次遍历来说，两两线段之间的距离是已知的。那么我们需要解决的问题就是纵坐标的影响范围。
我们不妨把纵坐标都取出来，离散化映射到\([1,T]\)之间的\(T\)个整数值，并将这些纵坐标表示为\(T-1\)段，其中第\(i\)段代表了第\(i\)个纵坐标和第\(i+1\)个纵坐标之间的部分，然后，我们设立数组\(c_i\)代表第\(i\)段被覆盖的次数。
这样，我们就可以用如下的算法流程计算矩形的面积：
\(1.\) 对于每一个线段，将其的\(k\)值累加到这个线段对应的若干个纵坐标区间
\(2.\) 计算面积：所有\(T-1\)个纵坐标区间对应的\(c\)值大于零的就说明这些部分的区间还存在，将存在的区间的长度累加起来，乘上当前线段与下一条线段之间的横坐标之差就是这两条线段之间的面积。
显然，这里需要我们维护一个区间内的区间加法，区间求和，这个就是线段树的事情了。
由于本题中的区间修改成对出现，互相抵消，所以我们可以不写带有\(lazytag\)的线段树。我们在线段树的每一个节点上维护两个值\(cnt\)和\(len\)，\(cnt\)代表这段区间被覆盖的次数，如果\(cnt>0\)则当前区间的\(len\)等于当前区间的纵坐标长度，反之\(len_p=len_{p*2}+len_{p*2+1}\)。那么对于每一次区间修改，我们直接在线段树上改\(cnt\)的值即可，并沿路更新\(len\)值即可。
\(Code:\)
#include <bits/stdc++.h>
using namespace std;
const int N=120;
struct line
{
double x,d,u;int flag;
}a[N<<1];
struct node
{
int l,r,cnt;
double len;
}v[N<<3];
int n,t,val[N<<1][2],T;
double raw[N<<2],ans;
inline bool compare(line p1,line p2){return p1.x<p2.x;};
inline void input(void)
{
for (int i=1;i<=n;i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
a[2*i-1] = (line){x1,y1,y2,1};
a[2*i] = (line){x2,y1,y2,-1};
raw[++t] = y1 , raw[++t] = y2;
}
sort(a+1,a+2*n+1,compare);
}
inline void discrete(void)
{
sort(raw+1,raw+t+1);
t = unique(raw+1,raw+t+1) - (raw+1);
for (int i=1;i<=2*n;i++)
{
val[i][0] = lower_bound(raw+1,raw+t+1,a[i].d) - raw;
val[i][1] = lower_bound(raw+1,raw+t+1,a[i].u) - raw;
}
}
inline void updata(int p)
{
if (v[p].cnt>0) v[p].len = raw[v[p].r+1] - raw[v[p].l];
else if (v[p].l==v[p].r) v[p].len = 0;
else v[p].len = v[ p<<1 ].len + v[ p<<1|1 ].len;
}
inline void build(int p,int l,int r)
{
v[p].l = l , v[p].r = r;
if (l==r){v[l].cnt = v[l].len = 0; return;}
int mid = l+r >> 1;
build( p<<1 , l , mid );
build( p<<1|1 , mid+1 , r );
}
inline void modify(int p,int l,int r,int delta)
{
if (l<=v[p].l&&r>=v[p].r)
{
v[p].cnt += delta;
updata(p); return;
}
int mid = v[p].l+v[p].r >> 1;
if (l<=mid) modify( p<<1 , l , r , delta );
if (r>mid) modify( p<<1|1 , l , r , delta );
updata(p);
}
inline double query(void){return v[1].len;}
inline void solve(void)
{
for (int i=1;i<=2*n;i++)
{
modify(1,val[i][0],val[i][1]-1,a[i].flag);
ans += (a[i+1].x-a[i].x) * query();
}
}
int main(void)
{
while ( scanf("%d",&n) && n )
{
ans = t = 0;
input();
discrete();
build(1,1,t);
solve();
printf("Test case #%d\nTotal explored area: %.2lf\n\n",++T,ans);
}
return 0;
}
<后记>
