『树状数组及其拓展运用』
<更新提示>
<第一次更新>
<正文>
树状数组
单点修改 区间和查询
众所周知,树状数组是一个可以维护区间前缀和的数据结构,普通的树状数组应该能够支持单点修改,区间查询的操作,其修改和查询的时间复杂度均为\(O(log_2n)\)。
\(Code:\)
inline int lowbit(int x){return x&(-x);}
inline void modify(int pos,int x)
{
for (;pos<=n;pos+=lowbit(pos))
c[pos] += x;
}
inline int query(int pos)
{
int res=0;
for (;pos;pos-=lowbit(pos))
res += c[pos];
return res;
}
其基础部分我们不再讲解,接下来,我们将利用树状数组的简单变形来解决更多的问题。
区间修改 单点查询
其实,区间修改,单点查询也是可以使用树状数组实现的,我们考虑如下数组:
这其实是差分数组,即原序列相邻两项的差,那么由定义可以得到:
这是一个前缀和,可以用树状数组求得。
对于区间修改问题,我们就可以直接利用差分数组的性质,将\(c_l\)位置和\(c_{r+1}\)进行对应的正负修改,在前缀和中,得到的体现就是区间修改。
\(Code:\)
inline int lowbit(int x){return x&(-x);}
inline void modify(int pos,int x)
{
for (;pos<=n;pos+=lowbit(pos))
c[pos] += x;
}
inline int query(int pos)
{
int res=0;
for (;pos;pos-=lowbit(pos))
res += c[pos];
return res;
}
inline void solve(void)
{
scanf("%d%d",&n,&m);
int last=0,val;
for (int i=1;i<=n;i++)
{
scanf("%d",&val);
modify(i,val-last);
last=val;
}
int op,x,y,k;
for (int i=1;i<=m;i++)
{
scanf("%d",&op);
if (op==1)
{
scanf("%d%d%d",&x,&y,&k);
modify(x,k);modify(y+1,-k);
}
if (op==2)
{
scanf("%d",&k);
printf("%d\n",query(k));
}
}
}
区间修改 区间和查询
对于该问题,我们同样需要引入差分数组\(d_i=a_i-a_{i-1}\)。但是,就这样还不足以完成区间和查询的操作,我们考虑展开求和式:
令\(d_i'=(i-1)d_i\),则
用树状数组维护两个前缀和\(d\)和\(d'\),就可以解决区间查询问题。对于区间修改,利用差分的方式对两个数组同时进行修改即可。
\(Code:\)
inline int lowbit(int x){return x&(-x);}
inline long long query(int index,int pos)
{
long long res=0LL;
if(index) {for(;pos;pos-=lowbit(pos))res+=d[pos];}
else {for(;pos;pos-=lowbit(pos))res+=d_[pos];}
return res;
}
inline void modify(int index,int pos,long long delta)
{
if(index) {for(;pos<=n;pos+=lowbit(pos))d[pos]+=delta;}
else {for(;pos<=n;pos+=lowbit(pos))d_[pos]+=delta;}
}
inline void init(void)
{
for(int i=1;i<=n;i++)
{
modify(1,i,a[i]-a[i-1]);
modify(0,i,(i-1)*(a[i]-a[i-1]));
}
}
inline void solve(void)
{
for(int i=1;i<=m;i++)
{
char order;int l,r;long long delta;
cin>>order;
if(order=='C')
{
scanf("%d%d%lld",&l,&r,&delta);
modify(1,l,delta); modify(1,r+1,-delta);
modify(0,l,(l-1)*delta); modify(0,r+1,r*(-delta));
}
if(order=='Q')
{
scanf("%d%d",&l,&r);
printf("%lld\n",(r*query(1,r)-query(0,r))-((l-1)*query(1,l-1)-query(0,l-1)));
}
}
}
二维树状数组
对于一个二维矩阵内的部分和,其实直接利用树状数组进行简单拓展就可以实现了。
修改如下定义:\(c_{ij}\)代表以\((i,j)\)为右下角,长度为\(lowbit(i)\),高度为\(lowbit(j)\)的矩形中所有元素的和。
然后和树状数组一样直接维护就可以了,修改,查询的时间复杂度均为\(O(log_2^2n)\)。
当然,求部分和也要用到二维前缀和求部分和的公式。
\(Code:\)
inline int lowbit(int x){return x&(-x);}
inline void modify(int x,int y,int delta)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=n;j+=lowbit(j))
c[i][j]+=delta;
}
inline int query(int x,int y)
{
int res=0;
for(int i=x;i;i-=lowbit(i))
for(int j=y;j;j-=lowbit(j))
res+=c[i][j];
return res;
}
在二维树状数组的定义中,也可以拓展出区间修改,单点查询和区间修改,区间查询等内容,但由于其运用不多,实现价值不大,代码内容繁琐,故不详细讲解。
类树状数组
接下来,我们将讲解类树状数组,即利用树状数组的结构与思想来实现其他不同于前缀和的功能。
单点修改 区间最值
以维护区间最小值为例,还是先重新定义:\(c_i\)代表原序列区间\([i-lowbit_i+1,i]\)中元素的最小值。
首先,我们需要能够根据原序列建立\(c\)数组,实现建树操作。
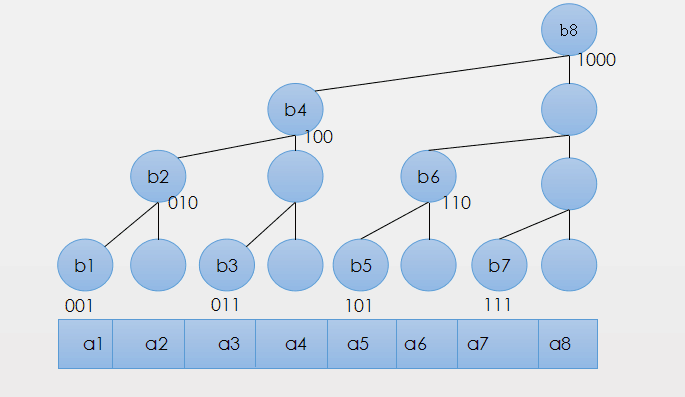
观察树状数组的基本结构图,我们发现对于求解\(c_i\),其树结构上的每一个子节点刚好包括了完整的\([1,i]\)区间。
又因为其子节点的\(c\)值都是已经求得的,所以,我们可以使用类似于递推的方法来更新\(c_i\)的值,更新一个节点的时间复杂度为\(O(log_2n)\),则建树的时间复杂度为\(O(nlog_2n)\)。
\(Code:\)
inline void build(void)
{
for (int i=1;i<=n;i++)
{
c[i] = a[i];
int sec = lowbit(i);
for (int j=1;j<sec;j*=2)
c[i] = max( c[i] , c[i-j] );
}
}
那么对于修改操作,其实我们套用树状数组的修改框架,利用相同的方式进行修改即可。时间复杂度为\(O(log_2^2n)\)。
\(Code:\)
inline void modify(int pos,int x)
{
a[pos] = x;
for (;pos<=n;pos+=lowbit(pos))
{
c[pos] = a[pos];
int sec = lowbit(pos);
for (int j=1;j<sec;j*=2)
c[pos] = max( c[pos] , c[pos-j] );
}
}
对于区间\([l,r]\)的最小值查询,由于我们已经得到了\(c\)数组,所以直接利用\(lowbit\)函数向左缩小区间,不断使用\(c\)数组更新答案即可,时间复杂度为\(O(log_2(r-l+1))\)。
\(Code:\)
inline int query(int l,int r)
{
int res = a[r];
while (true)
{
res = max( res , a[r] );
if (l==r)break;r--;
for (;r-l>=lowbit(r);r-=lowbit(r))
res = max( res , c[r] );
}
return res;
}
简单平衡树
树状数组可以实现基础平衡树中的如下操作:
\(1.\)增加元素
\(2.\)删除元素
\(3.\)查询排名
\(4.\)查询第\(k\)小值
\(5.\)查询前驱
\(6.\)查询后继
我们在值域上建立一个树状数组\(c\),\(c_i\)代表值域区间\([i-lowbit_i+1,i]\)中元素的个数。
由定义,我们就可以用树状数组的方法实现增加函数和删除函数了,其时间复杂度为\(O(log_2\max\{a_i\})\)。
\(Code:\)
inline void insert(int val,int cnt)
{
for (;val<=Uplim;val+=lowbit(val))
c[val] += cnt;
}
对于查询值\(val\)的排名,我们可以用树状数组方便地统计出值域\([1,val-1]\)上元素的个数,进而得到元素\(val\)的排名,实际复杂度为\(O(log_2val)\)。
\(Code:\)
inline int rank(int val)
{
int res=1;val--;
for (;val;val-=lowbit(val))
res += c[val];
return res;
}
对于查询排名为\(rank\)的数,我们需要使用倍增法解决。每一次我们使用\(2\)的整次方倍尝试扩展树状数组的值域下标,并累加元素个数,直到倍增的值恰巧符合要求即可。
\(Code:\)
inline int find(int rank)
{
int res=0,cnt=0;
for (int i=30;i>=0;i--)
{
res += (1<<i);
if ( res>Uplim || cnt+c[res]>=rank )//避免有多个值相同的元素
res -= (1<<i);
else cnt += c[res];
}
return ++res;
}
对于查询前驱和后继,可以直接利用以上两个函数实现。不过,两个函数分别有一些增减细节:
\(1.\)对于查询一个值的前驱,只需要查询排名比他小\(1\)的数即可,所以要减\(1\)
\(2.\)对于查询一个数的后继,只需要查询比它大\(1\)的数它的排名即可,这样可以防止有多个相同的数造成查询到同一个数,所以要加\(1\)
\(Code:\)
inline int prep(int val)
{
return find( rank(val)-1 );
}
inline int next(int val)
{
return find( rank(val+1) );
}
总结
树状数组在维护前缀和方面有很好的表现,也能够拓展来维护最值,排名,第\(k\)大等。可以替代简单的线段树,平衡树,并且代码量极小,时间表现也不错,值得我们学习,可以在适时灵活运用。
<后记>


