『土地征用 Land Acquisition 斜率优化DP』

<更新提示>

<第一次更新> 斜率优化DP的综合运用，对斜率优化的新理解。
详细介绍见『玩具装箱TOY 斜率优化DP』

---

<正文>

土地征用 Land Acquisition(USACO08MAR)#

Description#

Farmer John is considering buying more land for the farm and has his eye on N (1 <= N <= 50,000) additional rectangular plots, each with integer dimensions (1 <= width_i <= 1,000,000; 1 <= length_i <= 1,000,000).

If FJ wants to buy a single piece of land, the cost is $1/square unit, but savings are available for large purchases. He can buy any number of plots of land for a price in dollars that is the width of the widest plot times the length of the longest plot. Of course, land plots cannot be rotated, i.e., if Farmer John buys a 3x5 plot and a 5x3 plot in a group, he will pay 5x5=25.

FJ wants to grow his farm as much as possible and desires all the plots of land. Being both clever and frugal, it dawns on him that he can purchase the land in successive groups, cleverly minimizing the total cost by grouping various plots that have advantageous width or length values.

Given the number of plots for sale and the dimensions of each, determine the minimum amount for which Farmer John can purchase all

约翰准备扩大他的农场，眼前他正在考虑购买N块长方形的土地。如果约翰单买一块土 地，价格就是土地的面积。但他可以选择并购一组土地，并购的价格为这些土地中最大的长 乘以最大的宽。比如约翰并购一块3 × 5和一块5 × 3的土地，他只需要支付5 × 5 = 25元， 比单买合算。 约翰希望买下所有的土地。他发现，将这些土地分成不同的小组来并购可以节省经费。 给定每份土地的尺寸，请你帮助他计算购买所有土地所需的最小费用。

Input Format#

• Line 1: A single integer: N

• Lines 2..N+1: Line i+1 describes plot i with two space-separated integers: width_i and length_i

Output Format#

• Line 1: The minimum amount necessary to buy all the plots.

Sample Input#

Copy
4 
100 1 
15 15 
20 5 
1 100

Sample Output#

Copy
500

解析#

这是一道$USACO$的题，相比之前的玩具装箱，难度较大，我们通过这道题来更透彻地理解斜率优化$DP$。
显然，这不是一道明显的$DP$题，我们需要先做一些转换。有一个很明显的贪心，如果一块土地$P$的长和宽都大于另一块土地$Q$的话，那么显然$Q$我们是可以无视的，应为我们在购买$P$时，可以顺便购买$Q$，不会带来任何额外的花费。

STEP 1: 解决预备问题#

• 为了建立合适的$DP$模型，我们先要处理题面中的一些其他的问题。

这里我们使用栈来解决无用土地这个问题。
先将所有土地存入一个结构体中，然后就可以以长度$l$为第一关键字，宽度$w$为第二关键字对土地进行排序。排序完成后，我们需要将土地一一加入栈。
在加入一块土地时，我们需要检查:栈顶的土地的宽度是否小于等于这块土地的宽度，由排序可知，栈顶的土地的长度一定小于等于这块土地的长度，如果栈顶的土地的宽度也小于等于这块土地的宽度的话，我们就可以判定当前栈顶的土地是一块无用土地。那么，可以将栈顶土地直接弹出。
最后，栈中剩下的土地就是有效的土地。我们将其重新取出，并重新以长度$l$为第一关键字，宽度$w$为第二关键字对土地进行排序。

STEP 2: 建立DP模型#

• 在处理完其他问题后，我们需要建立朴素$DP$模型。

这时候，如果我们将所得的有效土地视为一个个矩形，排序后，放在平面直角坐标系中应满足：长度$x$随着下标的增大而增大，高度$y$随着下标的增大而减小，如下图所示。

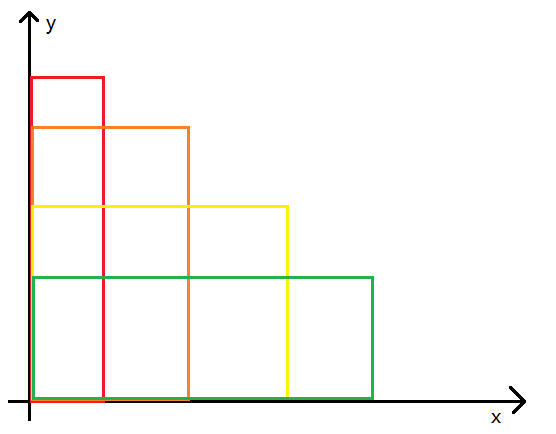
设$f_i$代表购买了前i块土地的最小花费，利用排序后的性质，那么我们就可以建立状态转移方程:

$$f_i=\min_{j<i}\{y_{j+1}x_i+f_j\}$$

STEP 3: 建立斜率函数#

• 得到了$DP$方程后，观察得知，方程形如$f_i=min/max\{a_i+b_j+kc_id_j+f_j\}$，即:方程中除了含有$f_j$以及单独和$i,j$有关的项外，还含有既和i有关，又和j有关的项。对于这种方程，我们考虑斜率优化。首先，我们需要利用状态转移方程建立斜率函数。

加入我们找到了最优的$f_j$，那么由方程可得:

$$f_i=y_{j+1}x_i+f_j \\⇒f_j=-y_{j+1}x_i+f_i$$

通常，我们视$f_j$为$y$，既和$i$有关，又和$j$有关的项中，视和$i$有关的部分为$k$，和$j$有关的部分为$x$，方程中的其余项为$b$。那么就可以得到斜率函数$y=kx+b$。
这里，出现了一种特殊情况:既和$i$有关，又和$j$有关的项是负数，那么我们通常将负号看做是与$y$有关的项的。
那么结果就是:视$f_j$为$y$，视$-y_{j+1}$为$x$，视$x_i$为$k$，视$f_i$为$b$，得到$y=kx+b$。

STEP 4: 分析单调性及凸包的性质#

• 得到斜率函数后，我们需要通过图像分析其性质，完成代码实现。

首先，我们得出函数的性质:

1.过定点$P_j(-y_{j+1},f_j)$
2.斜率为$x_i$

再通过我们之前得出的性质:土地高度$y$随着下标的增大而减小，以及花费$f_j$满足随着$j$的增大而增大，可以画出如下图像。

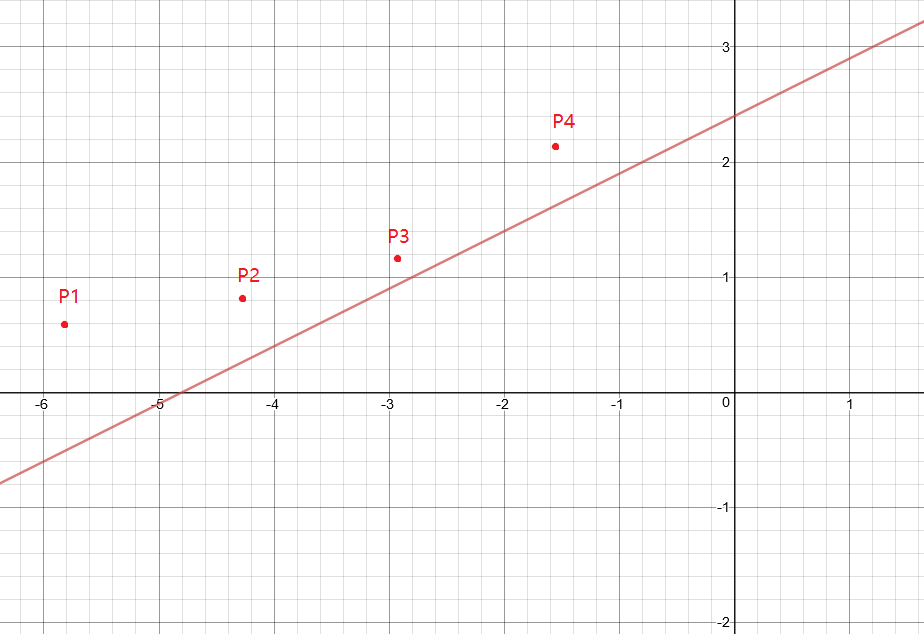
满足斜率为$x_i$的直线自上向下移动，由于我们需要截距$f_i$最小，当他碰到第一个$P_j$时，我们便得到了最优决策$j$。

注意到$x_i$满足单调上升，$P$点围成的凸包的两两节点之间的斜率也满足单调递增，就可以得到如下性质。

1.$slope(P_j,P_{j+1})>x_i$且$slope(P_{j-1},P_j)<x_i$时，$j$为最优决策，否则$j$永远不会成为最优决策
2.$slope(P_x,P_y)>slope(P_x,P_{y'})$，决策$y'$优于$y$

确认其具有如上性质后，单调队列维护即可。

STEP 5: 代码实现#

• 确立作法后，我们需要代码实现

注意事项

1.斜率函数中的斜率满足单调递增(递减)时，可以使用单调队列维护，转移均摊时间复杂度$O(1)$
2.斜率函数中的斜率不满足单调递增(递减)，但满足两两节点之间的斜率单调递增的凸包存在时(即性质$2$有效时)，可以使用单调栈维护，二分查找找到最优决策，转移均摊时间复杂度$O(log_2n)$
3.$slope$函数的返回值为$double$类型
4.注意是否需要开长整型变量$(longlong)$

$Code:$

Copy
#include<bits/stdc++.h>
using namespace std;
const int N=50000+80;
struct earth{long long x,y;}a[N],Stack[N],d[N];
long long n,top=0,f[N],q[N*2],head=1,tail=1;
inline bool cmp(earth p1,earth p2){if(p1.x==p2.x)return p1.y<p2.y;else return p1.x<p2.x;}
inline void input(void)
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
		scanf("%lld%lld",&a[i].x,&a[i].y);
} 
inline void init(void)
{
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++)
	{
		while(top&&Stack[top].y<=a[i].y)top--;
		Stack[++top]=a[i];
	}
	for(int i=1;i<=top;i++)
	{
		d[i]=Stack[i];
	}
	sort(d+1,d+top+1,cmp);
}
inline double slope(long long p,long long q){return (f[q]-f[p])*1.0/(d[p+1].y-d[q+1].y);}
inline void dp(void)
{
	f[0]=0;
	for(int i=1;i<=top;i++)
	{
		while(head<tail&&slope(q[head],q[head+1])<d[i].x)head++;
		f[i]=f[q[head]]+d[q[head]+1].y*d[i].x;
		while(head<tail&&slope(q[tail-1],q[tail])>slope(q[tail-1],i))tail--;
		q[++tail]=i;
	}
}
int main(void)
{
	input();
	init();
	dp();
	printf("%lld\n",f[top]);
}

---

<后记>