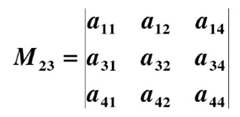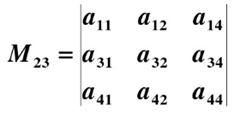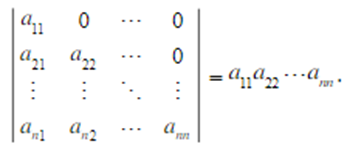【BZOJ】1002:轮状病毒(基尔霍夫矩阵【附公式推导】或打表)
Description
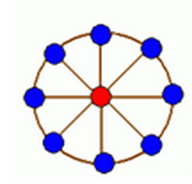
轮状病毒有很多变种,所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子
和圆心处一个核原子构成的,2个原子之间的边表示这2个原子之间的信息通道。如下图所示:
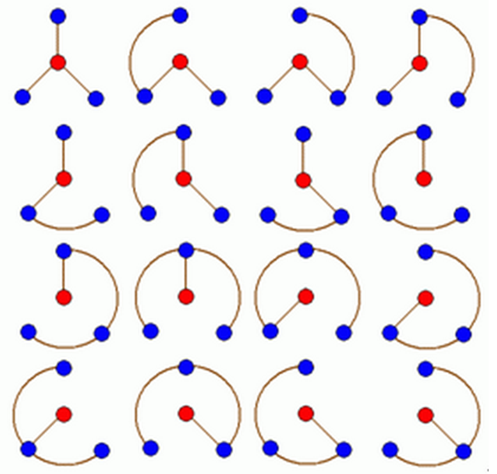
N轮状病毒的产生规律是在一个N轮状基中删去若干条边,使得各原子之间有唯一的信息通道,例如共有16个不
同的3轮状病毒,如下图所示:
现给定n(N<=100),编程计算有多少个不同的n轮状病毒。
Input
第一行有1个正整数n。
Output
计算出的不同的n轮状病毒数输出。
Sample Input
3
Sample Output
16
这里是题目链接:[BZOJ]1002:轮状病毒
这里是题解:
方法一:【打表找规律】
先暴力求出一部分答案:
这里是暴力打表代码:
 暴力打表
暴力打表#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define M 110 using namespace std; struct abcd{ int to,next; bool ban; }table[M<<2]; int head[M],tot=1; int n,ans; void Add(int x,int y) { table[++tot].to=y; table[tot].next=head[x]; head[x]=tot; } int fa[M],v[M],q[M],r,h; bool BFS() { int i; r=h=0; memset(v,0,sizeof v); memset(fa,-1,sizeof fa); q[++r]=0; while(r!=h) { int x=q[++h]; for(i=head[x];i;i=table[i].next) if(!table[i].ban) { if(table[i].to==fa[x]) continue; if(v[table[i].to]) return 0; fa[table[i].to]=x; v[table[i].to]=1; q[++r]=table[i].to; } } if(r<=n) return 0; return 1; } void DFS(int x) { if(x+x>tot) { if( BFS() ) ++ans; return ; } table[x<<1].ban=table[x<<1|1].ban=0; DFS(x+1); table[x<<1].ban=table[x<<1|1].ban=1; DFS(x+1); } int main() { int i; for(int j=1;j<=12;j++){ memset(head,0,sizeof head); tot=1;ans=0; n=j; for(i=1;i<=n;i++) Add(0,i),Add(i,0),Add(i,i%n+1),Add(i%n+1,i); DFS(1); cout<<ans<<' '; }printf("\n"); return 0; }
打出1-15的表(like this):
1 5 16 45 121
320 841 2205 5776 15125
39601 103680 271441 710645 1860496
Process exited after 48.06 seconds with return value 0
想将所有表打出来估计是不可能的事情,所以需要找规律。
这里是规律:
1 5 16 45 121 320 841 2205 5776 15125 39601 103680 271441 710645 1860496【1-15的答案】
第1、3、5、7...[奇数位]位是平方数 :
1*1 4*4 11*11 29*29 76*76 199*199 521*521...
第2、4、6、8...[偶数位]位除以5后也是平方数:
5*1*1 5*3*3 5*8*8 5*21*21 5*55*55 5*144*144 ...
【最美妙的事情发生了】:
奇数位:1 3 4 7 11 18 29 47 76...[粗体为原奇数位的算术平方根]
偶数位:1 2 3 5 8 13 21 34 55...[粗体为原偶数位除以5后的算术平方根]
(这个就属于改版的斐波拉契数列,只是初始值不一样)
然后求【改版斐波拉契数列】的值就行了。(但是要注意高精度!)
这里是推荐内容:
其实一般情况下还是很难看出来这个是改版斐波拉契数列的间隔值。
所以这里【倾情】推荐一个网站:Wolframalpha
这里输入之前打表的值:
然后这里就可以看见更多的值:
两三次【More】之后,基本上就有100个数了,然后就可以直接暴力打表。
【但是考场上不能用so sad :( 】
附:其实网上还流传了一种用这些打表出来的数:1 5 16 45 121 320 841 2205 5776 ……
得出了一个递推式:a[i]=a[i-1]*3-a[i-2]+2 ,用这个式子同样能够得出答案。
当然这个只是在[乱搞],找规律一般只使用于时间不够或者真的推不出来递推式的情况!
这里是找规律的代码:

#include <cstdio> #include <cstring> #include <algorithm> #include <iostream> using namespace std; struct Num { int a[1111],len; void Print() { for (int i=len-1;i>=0;i--) printf("%d",a[i]); printf("\n"); } }a[111],b[111]; int n; Num operator ^ (Num n,int b) { for (int i=0;i<n.len;i++) n.a[i]*=b; for (int i=0;i<n.len;i++) { n.a[i+1]+=n.a[i]/10; n.a[i]%=10; } while (n.a[n.len]!=0) { n.a[n.len+1]+=n.a[n.len]/10; n.a[n.len]%=10; n.len++; } return n; } Num operator * (Num a,Num b) { Num c; c.len=a.len+b.len; memset(c.a,0,sizeof c.a); for (int i=0;i<a.len;i++) for (int j=0;j<b.len;j++) c.a[i+j]+=a.a[i]*b.a[j]; for (int i=0;i<c.len;i++) { c.a[i+1]+=c.a[i]/10; c.a[i]%=10; } while (c.a[c.len-1]==0) c.len--; return c; } Num operator - (Num a,Num b) { for (int i=0;i<b.len;i++) a.a[i]-=b.a[i]; for (int i=0;i<a.len;i++) if (a.a[i]<0) { a.a[i]+=10; a.a[i+1]--; } while (a.a[a.len-1]==0) a.len--; return a; } void eq(Num &a,Num b) { a.len=b.len; for (int i=0;i<a.len;i++) a.a[i]=b.a[i]; } int main() { scanf("%d",&n); a[1].a[0]=1,a[2].a[0]=4; b[1].a[0]=1,b[2].a[0]=3; a[1].len=a[2].len=b[1].len=b[2].len=1; for (int i=3;i<=n;i++) { eq(a[i],(a[i-1]^3)-a[i-2]); eq(b[i],(b[i-1]^3)-b[i-2]); } Num ans; if (n%2==1) eq(ans,a[(n+1)/2]*a[(n+1)/2]); else eq(ans,b[n/2]*b[n/2]^5); ans.Print(); return 0; }
方法二:【基尔霍夫矩阵】
这里是预备知识:
这个题是求两两之间只有一条直接或间接路径(没有环,形成一棵树)的方案数。
一个专有名词叫做:【生成树计数】
生成树计数:通常情况是由Kirchhoff's Matrix-Tree Theorem(基尔霍夫矩阵矩阵树定理)求解。
基尔霍夫矩阵:也叫导纳矩阵、拉普拉斯矩阵或离散拉普拉斯算子。
给定一个有n个顶点的图G,它的拉普拉斯矩阵
定义为: L=D-A
其中:D矩阵叫做【度矩阵】;A矩阵叫做【邻接矩阵】
什么是度矩阵?
对于这种【无向图】,每一个点的度就是它连边的个数
【for example】:4的度数就是3(和3,5,6连边)
用这些度构成度矩阵:
仅当矩阵中【 i==j 】时D[i][j]才有值:此时D[i][j] = i 号点的度数
如果【 i!=j 】,D[i][j]就赋值为0.
所以上面这个图的度矩阵为:
什么是邻接矩阵?
当 i 号点和 j 号点有连边的时候,将A[i][j]=1,A[j][i]=1;(双向边)
其余 i、j 没有连边的 A[i][j]=0;
【当 i==j 时,A[i][j]=0 】
例子的邻接矩阵为:
所以基尔霍夫矩阵【 L=D-A 】为:

现在已经求得基尔霍夫矩阵,那么
Kirchhoff's Matrix-Tree Theorem(基尔霍夫矩阵矩阵树定理)又是什么呢?
基尔霍夫矩阵C的任意余子式Mij,Mij的行列式的值就是图G的生成树个数。
这里是大神博客:生成树计数问题——矩阵树定理及其证明
(证明见这位大神博客,蒟蒻表示不会证明这个,只会用ORZ)
什么是余子式?
简单来说就是:一个行列式的余子式Mij就是去掉aij所在的行和列。
(这里第三行删掉了,第三列也删掉了)
这里是本题真正的题解:
首先,根据以上条件,对于该图构造基尔霍夫矩阵。
(删除中心原点的行和列,设n为圈上的点的个数)
对角线aij表示与该点相连的个数。
如果i点和j点有连边,那么aij就赋值为-1.
(对于第一排和最后一排,因为这个图是一个圆圈,所以n与1相连)
然后计算出这个行列式的值就是本题的答案了,将该答案设为g[n]。
这里是计算过程:
方法①:高斯消元 O(n^3) 大概可以过吧,没写过ORZ。
方法②:利用行列式的性质推导。
(这里有一张大图,是推导全过程,结合此图浏览下列题解能更方便理解)
建议保存本图,然后用画图工具打开,边看图,边理解博客。
预备知识:(建议先了解行列式的各种性质)
对于本题,这里主要用两个性质:
1.n阶行列式,按行列展开。
展开方法:行列式等于它的任意一行(列)的各元素与其对应的代数余子式乘积之和。
代数余子式的计算方法:对于一个4阶行列式的余子式M23.
其代数余子式A23=M23*(-1)^(2+3)=-M23
所以公式为:Aij=Mij*(-1)^(i+j)
2.三角行列式的计算:主对角线以上的部分全为0。
注:建议先熟悉行列式的各种性质。
现在,将本题的行列式按最后一行展开。
最后一行第一项展开为:(为了之后方便,将其设为①号式子[n-1阶行列式])
最后一行倒数第二项展开为:(为了之后方便,将其设为②号式子[n-1阶行列式])
最后一行最后一项展开为:(为了之后方便,将其设为③号式子[n-1阶行列式])
因为③号式子形式特别,现将对角线为3,然后两边为-1的式子设为f[i]。
所以③号式子设为f[n-1].(注意这里和之前的基尔霍夫矩阵不一样,因为这里a1n、an1不再为-1)
原式=①号+②号+③号
对于①号式子:按第一行展开。
①号式子第一项展开得到下列式子[n-2阶式子]:
明显运用之前提到的性质2,可以求出,该式子的值为:(-1)^(n-1)
①号式子最后一项得到下列式子[n-2阶式子]:
明显这个矩阵就像f函数的矩阵形式。
所以①号式子的值可以表示为:-1-f[n-2]
对于②号式子:按最后一列展开。(注意是列)
②号式子按最后一列第一项展开得到下列式子[n-2阶式子]:
根据三角行列式计算方法,得到该行列式的值为:-1
②号式子按照最后一项展开得到下列式子[n-2阶式子]:
明显形式又是相同的,所以该行列式的值可以表示为:-f[n-2]
所以②号式子的值为:-f[n-2]-1
而对于③号式子:
本身形式相同,所以表示为:3*f[n-1]
综上g[n]=①+②+③=-1-f[n-2]-f[n-2]-1+3*f[n-1]=3*f[n-1]-2*f[n-2]-2
现在就要求出f函数之间的关系:
对于无系数的③号式子:按照最后一行展开。
倒数第二项展开为:(为了之后方便,将其设为④号式子[n-2]阶行列式])
最后一项展开为:([n-2]阶行列式)
明显这个形式就是之前的f函数,所以可以表示为:3*f[n-2].
对于④号式子:按照最后一行展开。
倒数第二项展开:
因为这个行列式中有一列为0,按照行列式的定义,它的值为0.
最后一项展开:([n-3]阶行列式)
这个行列式的值就可以表示为:-f[n-3].
所以④号式子的值为:-f[n-3].
根据③号式子、④号式子:可以得出f[n-1]=3*f[n-2]-f[n-3]
现在有两个式子:
g[n]=3*f[n-1]-2*f[n-2]-2
f[n]=3*f[n-1]-f[n-2]
如何将它化成一个只有g函数的递推式:
首先g函数与f函数的关系式为:g[i]=3*f[i-1]-2*f[i-2]-2
因为3*f[i-1]=9*f[i-2]-3*f[i-3]
且3*g[i-1]=9*f[i-2]-6*f[i-3]-6
所以(用g[i-1]来替代f[i-1])
g[i]=3*g[i-1]+3*f[i-3]+6-2*f[i-2]-2
=3*g[i-1]+3*f[i-3]-2*f[i-2]+4
又因为-2*f[i-2]=-6*f[i-3]+2*f[i-4]
所以(将g[i]中的f[i-2]展开)
g[i]=3*g[i-1]+3*f[i-3]-6*f[i-3]+2*f[i-4]+4
=3*g[i-1]-3*f[i-3]+2*f[i-4]+4
又因为:-g[i-2]=-3*f[i-3]+2*f[i-4]-2
所以:g[i]=3*g[i-1]-g[i-2]+2
g函数的初值:
g[1]=1、g[2]=5
这里是最终代码(注意高精度!):

#include<iostream> #include<cstdio> using namespace std; struct data{ int a[101],len; }; int n; data mul(data a,int k) { for(int i=1;i<=a.len;i++) a.a[i]*=k; for(int i=1;i<=a.len;i++) { a.a[i+1]+=a.a[i]/10; a.a[i]%=10; } if(a.a[a.len+1]!=0)a.len++; return a; } data sub(data a,data b) { a.a[1]+=2; int j=1; while(a.a[j]>=10){a.a[j]%=10;a.a[j+1]++;j++;} for(int i=1;i<=a.len;i++) { a.a[i]-=b.a[i]; if(a.a[i]<0){a.a[i]+=10;a.a[i+1]--;} } while(a.a[a.len]==0)a.len--; return a; } int main() { data f[101];f[1].a[1]=1;f[2].a[1]=5; f[1].len=f[2].len=1; scanf("%d",&n); for(int i=3;i<=n;i++) f[i]=sub(mul(f[i-1],3),f[i-2]); for(int i=f[n].len;i>0;i--) printf("%d",f[n].a[i]); return 0; }
这里还有一种大犇的证明:1002: [FJOI2007]轮状病毒 (值得一看orz)
梦想总是要有的,万一实现了呢?