[算法1-排序](.NET源码学习)& LINQ & Lambda
[算法1-排序](.NET源码学习)& LINQ & Lambda
说起排序算法,在日常实际开发中我们基本不在意这些事情,有API不用不是没事找事嘛。但必要的基础还是需要了解掌握。
排序的目的是为了让无序的数据,变得“有序”。此处的有序指的是,满足当前使用需求的顺序,除了自带的API,我们还可以自定义比较器对象、使用LINQ语句、Lambda表达式等方式完成排序。本文将逐一介绍十大排序,并着重介绍分析基于C#的LINQ常用语句和Lambda表达式,二者对排序的实现。
【# 请先阅读注意事项】
【注:(1)以下提到的复杂度仅为算法本身,不计入算法之外的部分(如,待排序数组的空间占用)且时间复杂度为平均时间复杂度
(2)除特殊标识外,测试环境与代码均为.NET 6/C#
(3)默认情况下,所有解释与用例的目标数据均为升序
(4)默认情况下,图片与文字的关系:图片下方,是该幅图片的解释
(5)本文篇幅较长,和主标题(排序)契合度较低,建议分期阅读;也可能存在较多错误,欢迎指出并提出意见,请见谅】
一. 十大排序
这十大排序对于有基础的程序员并不陌生,只是一些经常不用的小细节可能记忆模糊,该部分内容会对排序方法简要分析,旨在作为笔记,需要的时候帮助回忆相关内容。
(一) 冒泡排序(BubbleSort)
名字的起源十分生动形象:气泡从水底向上浮,随气压变化气泡体积逐渐变大最终破裂;在某一时刻让时间静止,可观察到从水面到水底,气泡体积依次减小,体积排列有序,故得此名。
1. 原理:两两比较,按照比较器对象进行交换。
2. 复杂度:时间O(n2) 空间O(1)
3. 实现:(C++14 GCC 9)

(指针形式)

(二) 选择排序(SelectSort)
1. 原理:选择——选定一个数,确定当前该数的位置后,再选择下一个数。注意其和冒泡排序的区别。
2. 复杂度:时间O(n2) 空间O(1)
3. 实现:(C++14 GCC 9)

二者区别在于:冒泡是相邻的数比较;选择是每次固定一个数与其他数比较。
(三) 插入排序(InsertSort)
其操作方式类似于我们再打牌时,抽出一些牌放入合适的位置。
1. 原理:选定一个数,将该数插入合适的位置。即,若排序结果为升序,则将数b插入某一位置,使得a < b < c。
2. 复杂度:时间O(n2) 空间O(1)
3. 实现:(C++14 GCC 9)

(四) 希尔排序(ShellSort)
此排序由希尔提出,是对插入排序的改进。改进的思想是:将一整个待排序序列分割为多个组,每一次对每个组的同一位置进行插入排序。即,将第一、二、三…组的第一个元素看为一个新的序列进行插排,第二个元素看为一个新的序列进行插排……以此类推。实验证明,该思想在一定程度上有助于加快插入排序的运行。
1. 原理:分割式插排
2. 复杂度:时间O(n1.3) 空间O(1)
3. 实现:(C++14 GCC 9)
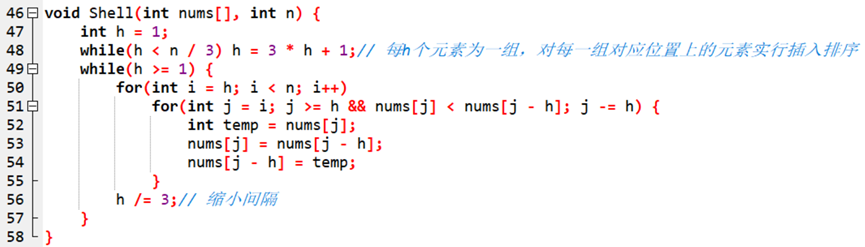
大量数据表明,当h /= 3时可达到最优效果。
(五) 快速排序(QuickSort)
快速排序是最常用的一个排序,在之前的介绍.NET数组源码的排序方法([数据结构-线性表1.1] 数组 (.NET源码学习))中也出现过,虽然其内部有三种排序方式,但主体还是快速排序。之所以称之为快速,是因为其时间复杂度不再是n2级,而是nlog2n级。一般地,在1s的时间范围内,总时间复杂级数需要小于等于108,快速排序的出现,解决了许多大量数据排序的问题,提高了不少效率。
1. 原理:类二分法
2. 复杂度:时间O(nlog2n) 空间O(log2n)
3. 实现:(C++14 GCC 9)
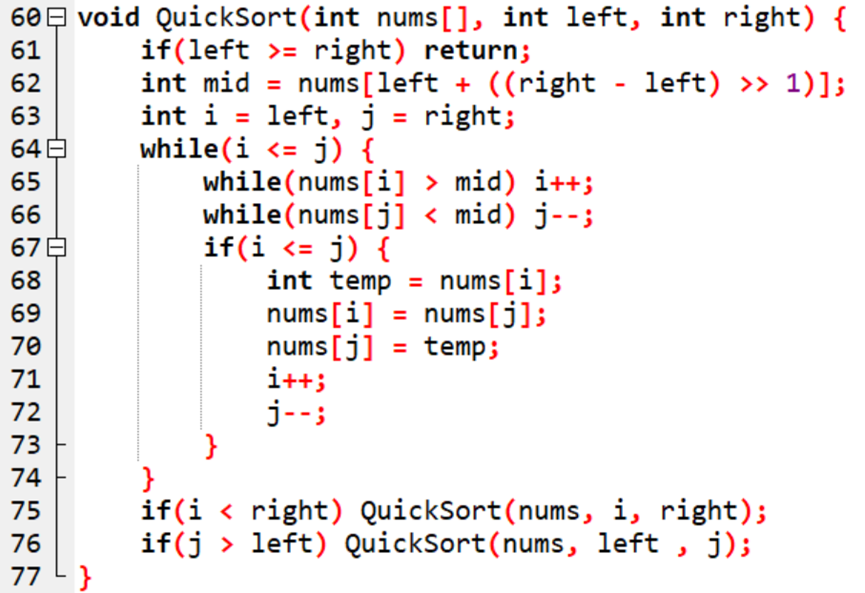
快速排序只是使用数组原本的空间进行排序,所以所占用的空间应该是常量级的,但是由于每次划分之后是递归调用,递归在运行的过程中会在栈上消耗一定的空间,在一般情况下的空间复杂度为O(logn),在最差的情况下,若每次只完成了一个元素,那么空间复杂度为O(n)。
[# Array.Sort()源码再读—有关快速排序]
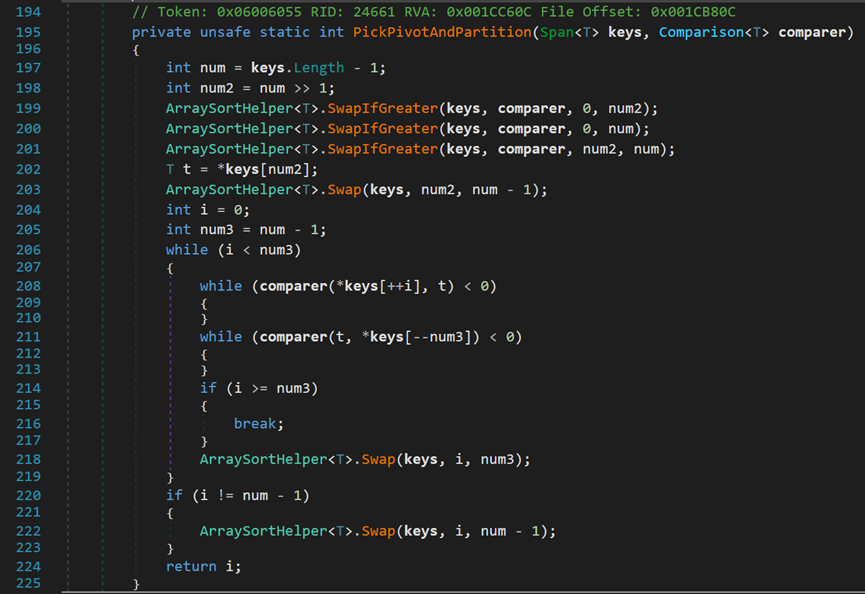
这是该方法中的快速排序,和我们一般的快速排序不同,其运用了SwapIfGreater()方法、三数取中法对快速排序进行了优化。
- Line 197:此处的num为数组长度。
- l Line 198:num >> 1 相当于 num / 2,一般地,可视为中间位置索引值。
- l Line 199~201:SwapIfGreater()方法
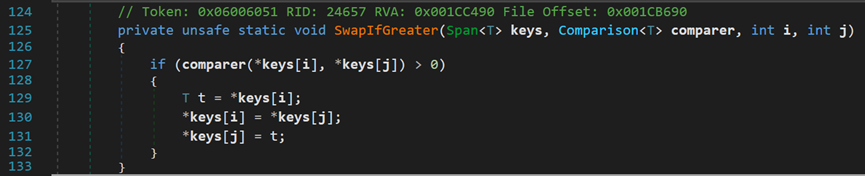
根据传入的比较器对象,对两个元素进行相应处理。
在排序前,其先把索引为0和mid的两个元素、索引为0的元素和最后一个元素、索引为mid的元素和最后一个元素进行处理,优先保证这三个位置上的元素符合要求。
该方法即为三数取中法。
1. 方法:是知道无序数列的首和尾,便可以求出其中间位置的数,此时只需在首、中、尾这三个数中,选择中间的这个数作为基准值,进行快速排序,即可进一步提高快速排序的效率。
最初的快速排序是选择第一个或最后一个元素为基准值,然后将整个序列分为两部分。但当数组本身有序度较高或完全有序时,快排会达到O(n2)的时间复杂度,因为可能会导致分完后的两部分中,某一部分为空集。即,相当于没有二分就开始排序。
2. 优化原理:将首、中、尾排序后,选取中间位置的元素,能有效避免“一边倒”的问题,从而真正利用上二分思想的加速性。
- Line 202:t 即为基准值。
- Line 203:交换中间位置和末尾的元素。使得这三个元素大小变成“峰谷”状,由于基准值是三个元素中间大小的一个,这样相当于保证分成的两部分不出现空集。
该源码和本人写的代码格式不同,本人运用递归的方法,将序列无限二分至无法再分,先左后右逐步有序;源码利用迭代方法,三数取中 + 双向搜索,从整体到局部。虽然平均复杂度均为log级,但长远看来源码具有较高的优越性。
- Line 206~218:从两端开始,以中间位置为中心、基准值为判断依据开始交换。
当最外层while循环结束后,i的左侧一定全都是小于基准值的元素,num3的右侧一定全都是大于基准值的元素。此时,相对于基准值而言,i的左侧是有序的,num3的右侧是有序的。
- Line 220~223:将i位置的元素与末尾元素交换。此时i位置的元素,是大于等于末尾元素的。交换后,从开头到i位置的元素相对于刚才而言,更加有序。

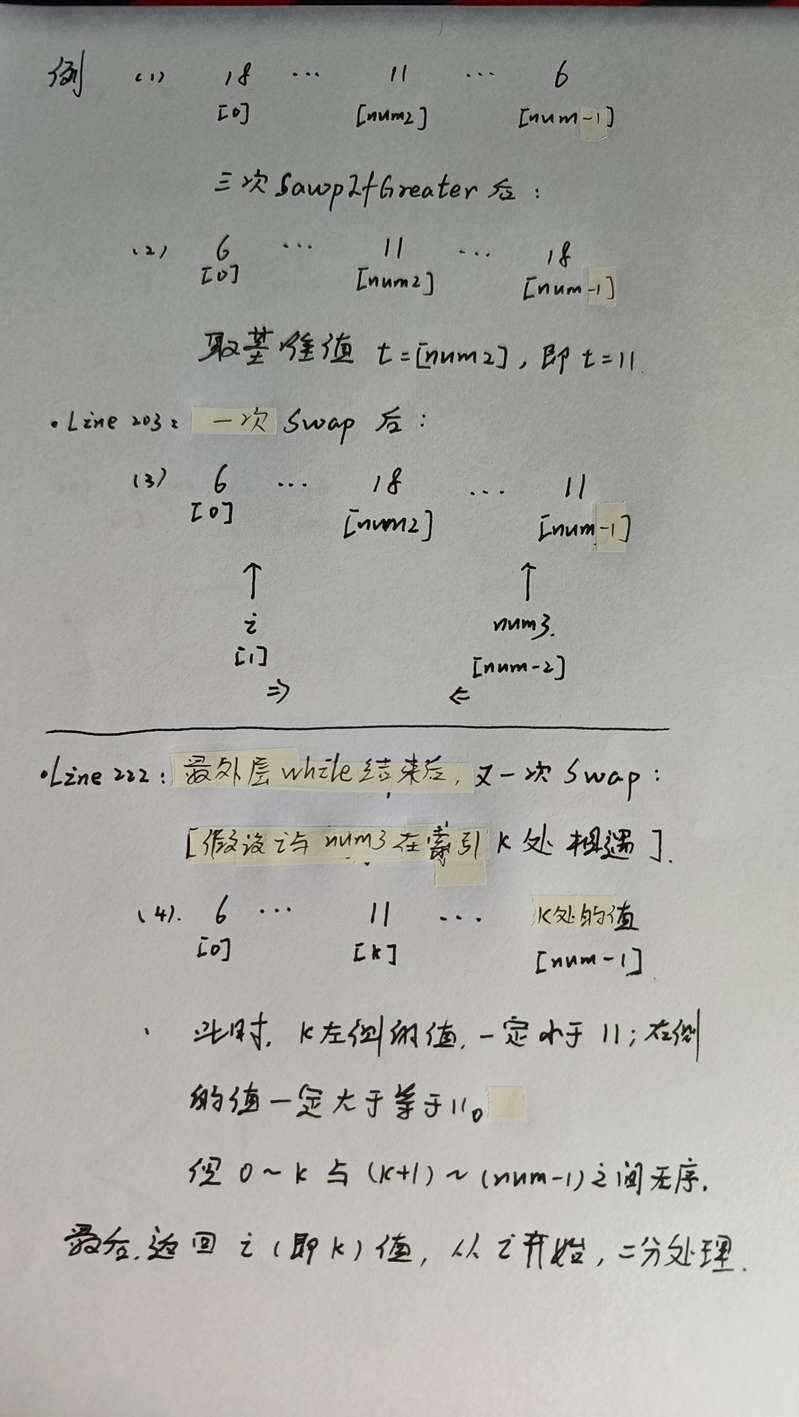
上图是本人手写的一份基本流程草图,该快速排序有别于一般形式的快速排序,但整体思想依旧不变:类二分法,从子集有序到整体有序,加上两种方法的优化,效率已经是很高的了。
(六) 归并排序
归并,即合并,既然要合并,那之前就得拆开。所以,归并排序的方法就是先把元素二分,二分后每段再二分,直到无法二分。再根据比较器对象,按一定顺序合二为一,逐层回调,最后完成排序。
1. 原理:类二分法
2. 复杂度:时间O(nlog2n) 空间O(n)
3. 实现:(C++14 GCC 9)

快速排序是先排序,使得整个序列以基准值有序,再二分;归并排序是直接二分到底,再逐层往回排序,从局部到整体。
(七) 堆排序
堆的结构类似于二叉树,而二叉树的相关操作(如,查询、插入、删除等)的时间复杂度一般都在常数级和log级,所以堆排序的效率也比较高。
1. 原理:根据数组索引和二叉树位置的关系,构建大/小顶堆(二叉树)并还原。
2. 复杂度:时间O(nlog2n) 空间O(1)
3. 实现:(C++14 GCC 9)

一般地,目标为升序数组则构建大顶堆,目标为降序数组则构建小顶堆。
[# Array.Sort()源码再读—有关堆排序]
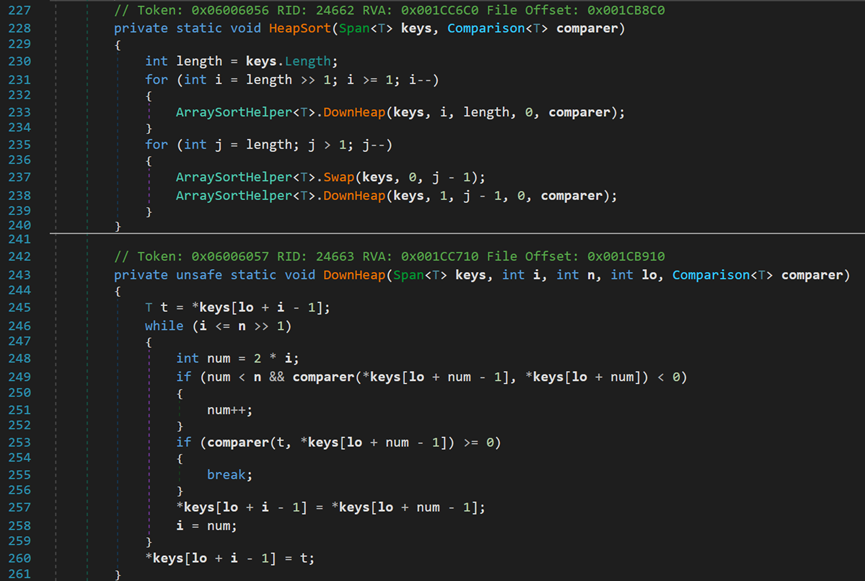
该源码与一般的堆排序写法如出一辙,上方的HeapSort()方法用于控制每次调整堆的范围,保证有序元素不再被调整;下方的DownHeap()方法用于构建/调整堆,将合适的元素放到合适的位置。
- Line 231~234:第一次构建堆,构建大顶堆。即,让每一个父结点的值大于等于子结点的值。
- Line 235~239:调整堆。每次调整后,根节点总是最大的,所以将根节点与最后一个非调整好的结点(从右下角开始往前)进行交换,交换后靠近末尾的部分元素已经是有序的了,所以下一次调整堆顶时,应将其排除在外,这就是参数中j – 1的由来。
- Line 243:参数:keys为待排序元素集;i为排序起始位置的索引(由于第一次构建堆顶时,保证了父结点的值大于等于子结点的值,所以交换后0索引处的值一定是较小的值,且该位置是一个动态存储域,所以调整的其实索引可以从1开始,这就是传入值为1的原因);n为排序结束的索引;lo为应当进行交换的元素的索引(堆排序在建好堆后,一般从最后一个非叶子结点开始进行判断。即,从最后一个分支,倒着往前进行。对于数组索引即为2 * 起始索引 + 1);
之后的过程和本人以C++语言所写的过程大体相似。
(八) 计数排序、桶排序
理论上这两者排序的思想是类似的:新建数组,以索引代表元素,统计每个元素出现次数,最后再输出。
1. 原理:按索引顺序,以索引值代表数组值,统计出现次数。
2. 复杂度:时间O(n + k) 空间O(n + k)(其中,k为max – min)
3. 实现:(C++14 GCC 9)
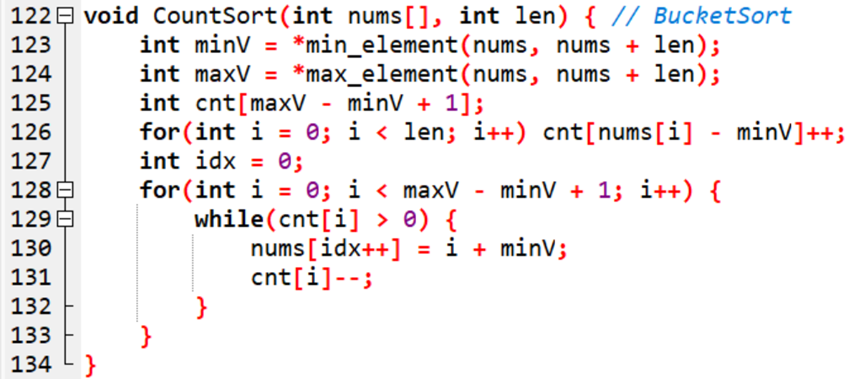
当然,从标准出发,这二者肯定是不一样的。
对于桶排序,将待排序元素划分到不同的痛。先扫描一遍序列求出max和min ,设桶的个数为 k ,则把区间 [min, max] 均匀划分成 k 个区间,每个区间就是一个桶,将序列中的元素分配到各自的桶。
对于计数排序,每个数值为一个桶。计数排序本质上是一种特殊的桶排序,当桶排序的桶的个数最大的时候,就是计数排序。
(九) 基数排序
1. 原理:按照元素的每一位进行比较来排序。
2. 复杂度:时间O(n * k) 空间O(n + k) (其中,k为max – min)
3. 实现:(C++)来自(1.10 基数排序 | 菜鸟教程 (runoob.com))

小结一
基数排序与计数排序、桶排序这三种排序算法都利用了桶的概念,但对桶的使用上有一定差异:
(1)桶排序:每个桶存储一定范围的数值;
(2)计数排序:每个桶只存储单一键值;
(3)基数排序:根据键值的每位数字来分配桶;
基数排序不是直接根据元素整体的大小进行元素比较,而是将原始列表元素分成多个部分,对每一部分按一定的规则进行排序,进而形成最终的有序列表。
LINQ语句及常用方法
LINQ(Language-Integrated Query)语言集成查询,常用于对数据的查询。一般地,完整的查询操作包括创建数据源、定义查询表达式和在foreach语句中执行查询。

该部分将分析相关方法的源码,以及内部的orerby与orderbyDescending排序方法。本人会尽可能的讲述清楚过程的细节,但之前也没有详细读过源码,该文章也是边读边学边写,可能存在解读错误,也可能会有与读者相矛盾的观点,还望各位指出,请谅解。
(一) All()方法
确定序列的所有元素是否都满足条件。

- Line 10:LINQ方法中的参数并不像一般方法中的参数一样,各个对应。
- Line 12~15:检查源数据是否为空,防止访问没有分配引用地址的对象。
- Line 16~19:检查过滤器对象是否为空。
- Line 20~27:对每个元素根据传入的委托表达式进行判断。
对于这两个参数,可以发现:


(一) 不管是在源码还是在从元数据中,该方法均有两个参数。但在使用时,却只需要传入一个参数。
(二) TSource和泛型T不是一个东西,泛型T可以容纳所有类型,但需要手动指定数据类型;TSource可以容纳所有类型,但可自动识别类型。
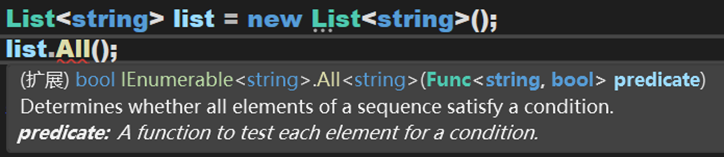
当要访问的元素集是什么类型时,TSource会自动分配对应的类型。
(三) 待传入的参数Func<TSource, bool> predicate是一个方法(称为此处过滤器),将方法作为参数,无疑用到了委托。

关键字in和out一般用在泛型interface和delegate中, 用来进行逆变和协变(in逆变,out协变)。(协变、逆变将在下方介绍)
Func()方法是一个有返回值的泛型委托,可包含0~16个参数T,并在最后多加一个参数,表示返回值类型。我们也可以自己定义该方法,如:
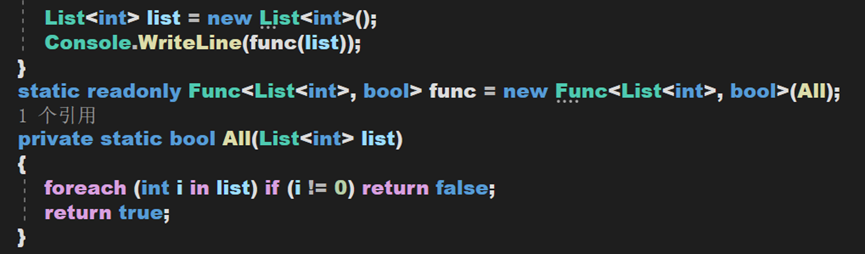
根据我们自己写的调用的操作步骤,可以发现,我们只需传入待处理参数,不用管最后的返回参数。

其基本语法格式为:方法名(临时变量 => 条件表达式)。其中,括号中的式子称为Lambda表达式,会在后文介绍。
(二) Any()方法
判断是否包含任何元素、是否存在元素满足指定的条件。

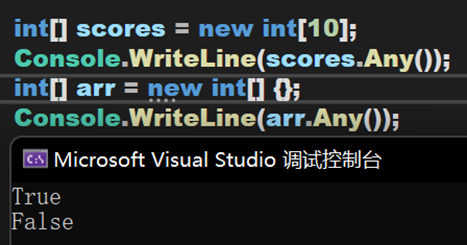
(1)首先是判断源数据是否包含任何元素。

- Line 15~29:尝试将source转换为集合(接口)类型,若转换成功,即序列可以作为ICllection<>的实例,则通过返回Count属性,判断其是否包含任何的元素。
- Line 20~35:尝试将source转换为IListProvider(接口)类型,若转换成功,则调用GetCount()方法,默认传入true,进行判断;而否则尝试转换为集合类型。
- Line 37~42:提取source的迭代器对象,判断其是否存在下一个元素,如果枚举数已成功地推进到下一个元素,返回true;如果枚举数传递到集合的末尾,返回false。
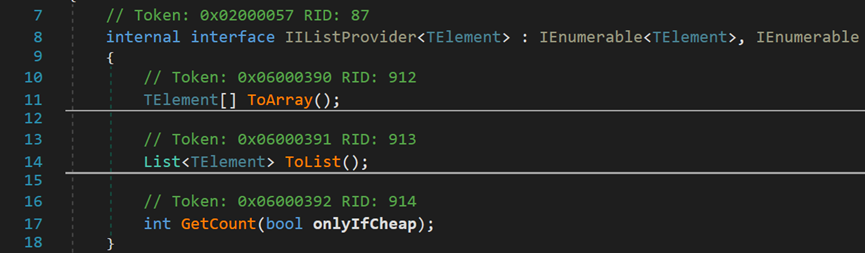
对于IListProvider,其内部包含了三个方法:转换为数组、转换为泛型集合、GetCount()方法。
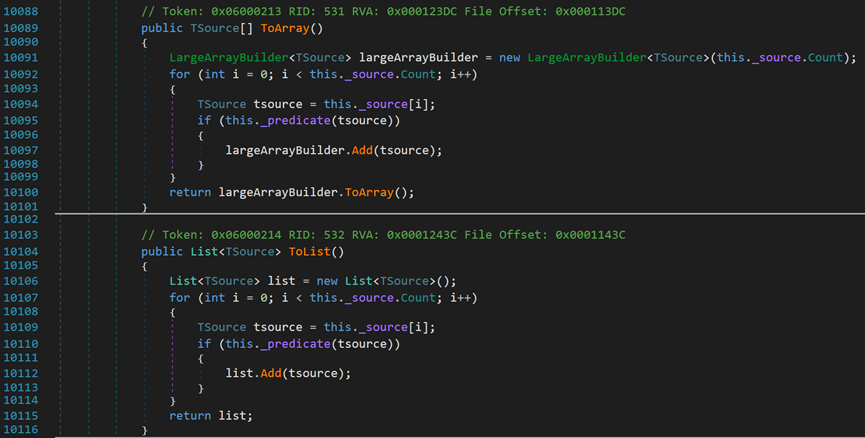
其中,前两个方法的实现均是将元素放入到新的数据结构中,最后返回。内部的字段_source[]指的是源数据及,_predicate()方法指的是传入的条件表达式;LargeArrayBuilder可以近似看作StringBuilder。
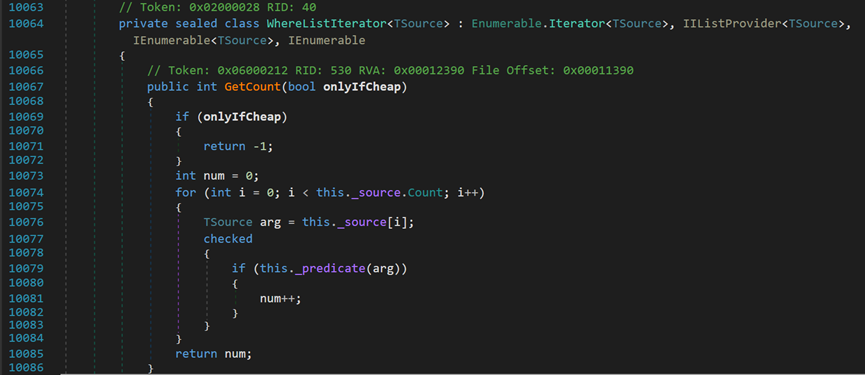
对于GetCount()方法,其原理也是通过遍历源数据集,在满足相应条件的情况下记录元素个数。
(2)判断源数据是否包含任意一个符合条件的元素
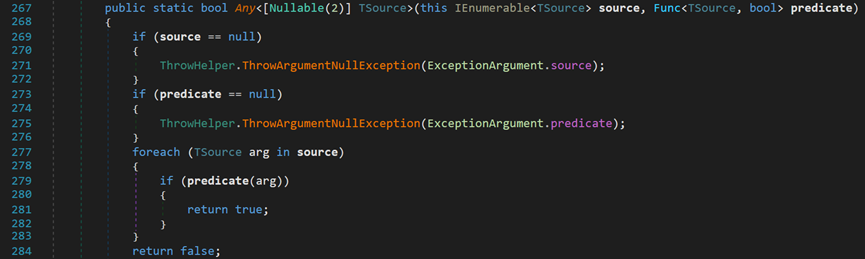
通过遍历的方式逐一检查,存在一个满足条件就返回true,一个都不满足就返回false;
(三) 基本计算--Count()、Max()、Min()、Sum()方法
(1)Count()方法
其包含两个重载形式:一个是纯计数,另一个是带条件计数(记录满足条件的元素个数)。
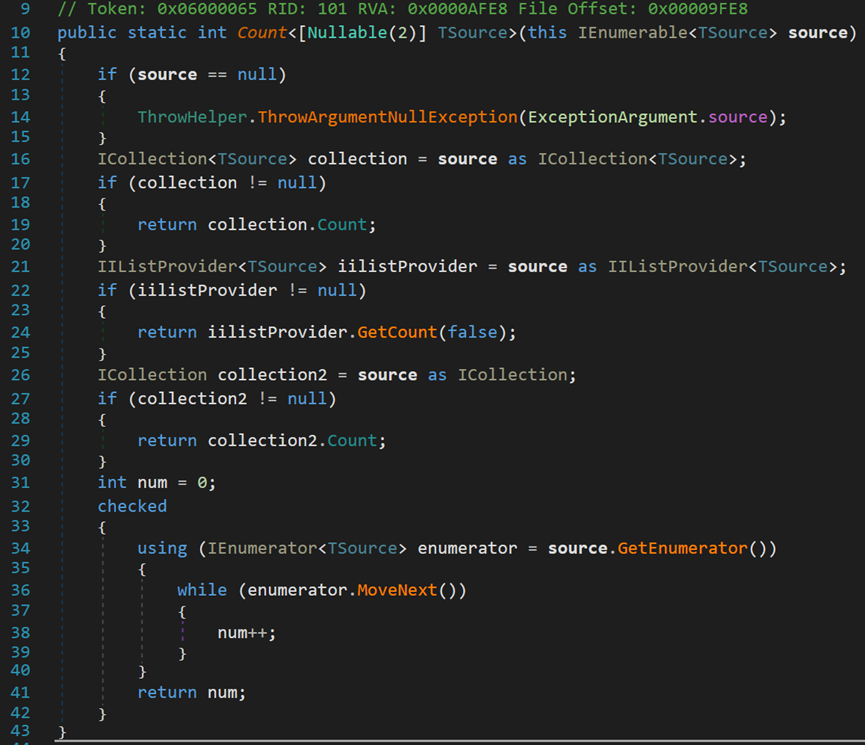
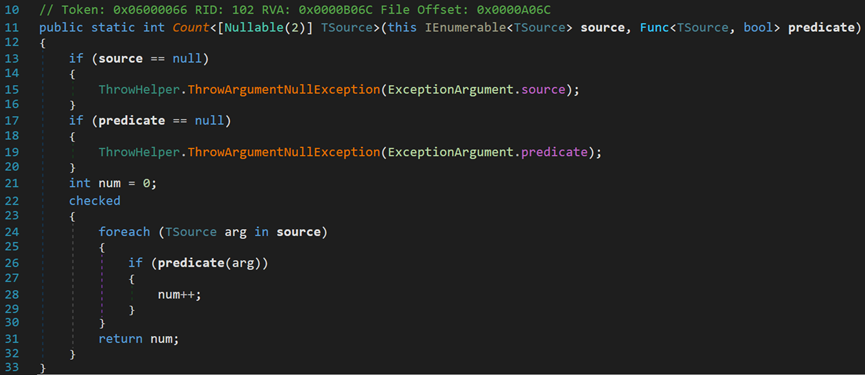
可以发现,其原理和Any()方法中的GetCount()方法基本类似。
(2)Max()、Min()、Sum()方法
这三种方法,前两种每种包含21个重载函数,Sum()方法包含19个重载函数,因为需要针对不同的数据类型。但最大不同依旧在于是否带有条件。
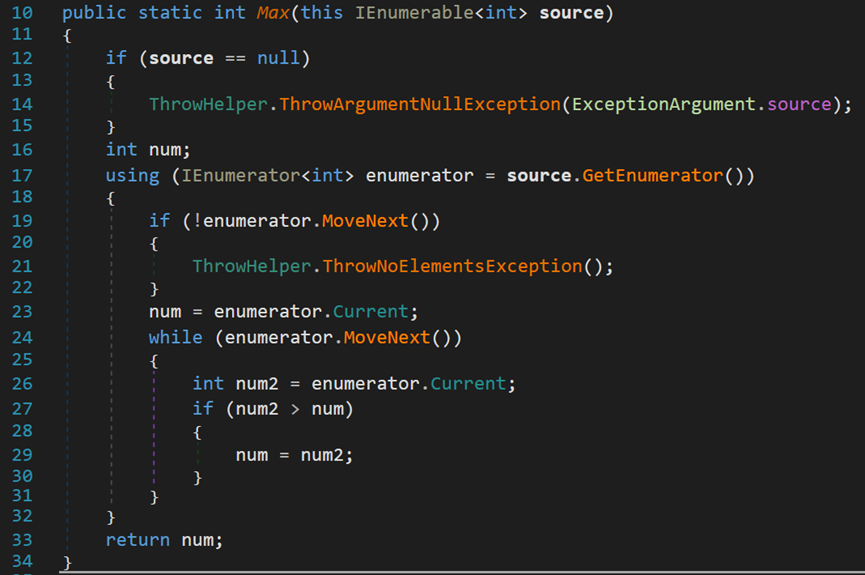
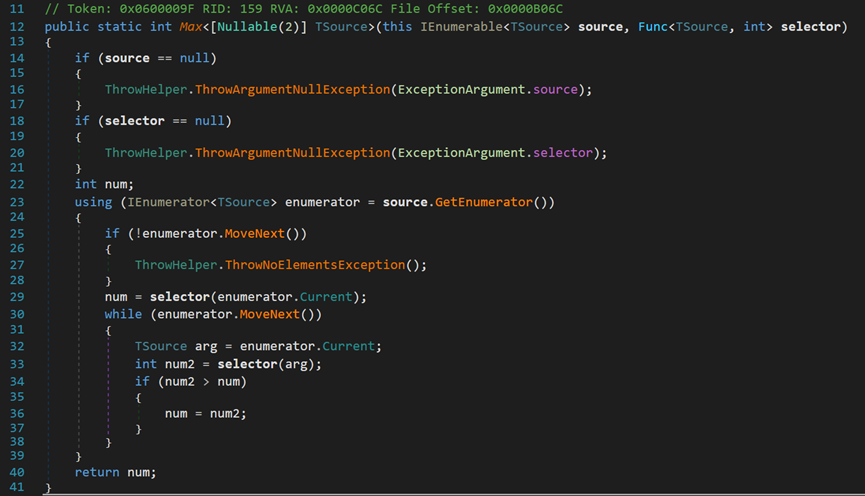
其实现原理基本类似,且没有什么新的东西,所以在此不做过多论述。
(四) Where的实现
Where子句用在查询表达式中,用于指定将在查询表达式中返回数据源中的哪些元素。它将一个布尔条件应用于每个源元素(由范围变量引用),并返回满足指定条件的元素。一个查询表达式可以包含多个Where子句,一个子句可以包含多个条件表达式。简而言之,Where起到一个筛选器的作用,筛选出符合条件的元素。

并且可以发现,筛选出的元素默认情况下共同构成一个可枚举的集合。
Where方法的过滤功能主要通过迭代器实现,其源代码包含7个迭代器。按照功能划分如下:
(1)索引参与过滤操作运算的迭代器WhereIterator,容器(可迭代对象)包含Enmuerable,List和Array。
(2)索引不参与过滤运算
1. Enmuerable:WhereEnumerableIterator和WhereSelectEnumerableIterator
2. List:WhereListIterator和WhereSelectListIterator
3. Array:WhereArrayIterator和WhereSelectArrayIterator

其中Enmuerable迭代器,List迭代器和Array迭代器在实现上相差不大,都是通过设计模式中的迭代器模式实现具体的功能。区别是Enmuerable迭代器,List迭代器都是调用容器自身的迭代器实现逐个元素的比较和过滤,而Array迭代器是通过数组索引操作实现元素比较和过滤。
除了WhereIterator,其余六个迭代器均派生自迭代器类Iterator
[# 有关Iterator的源码]
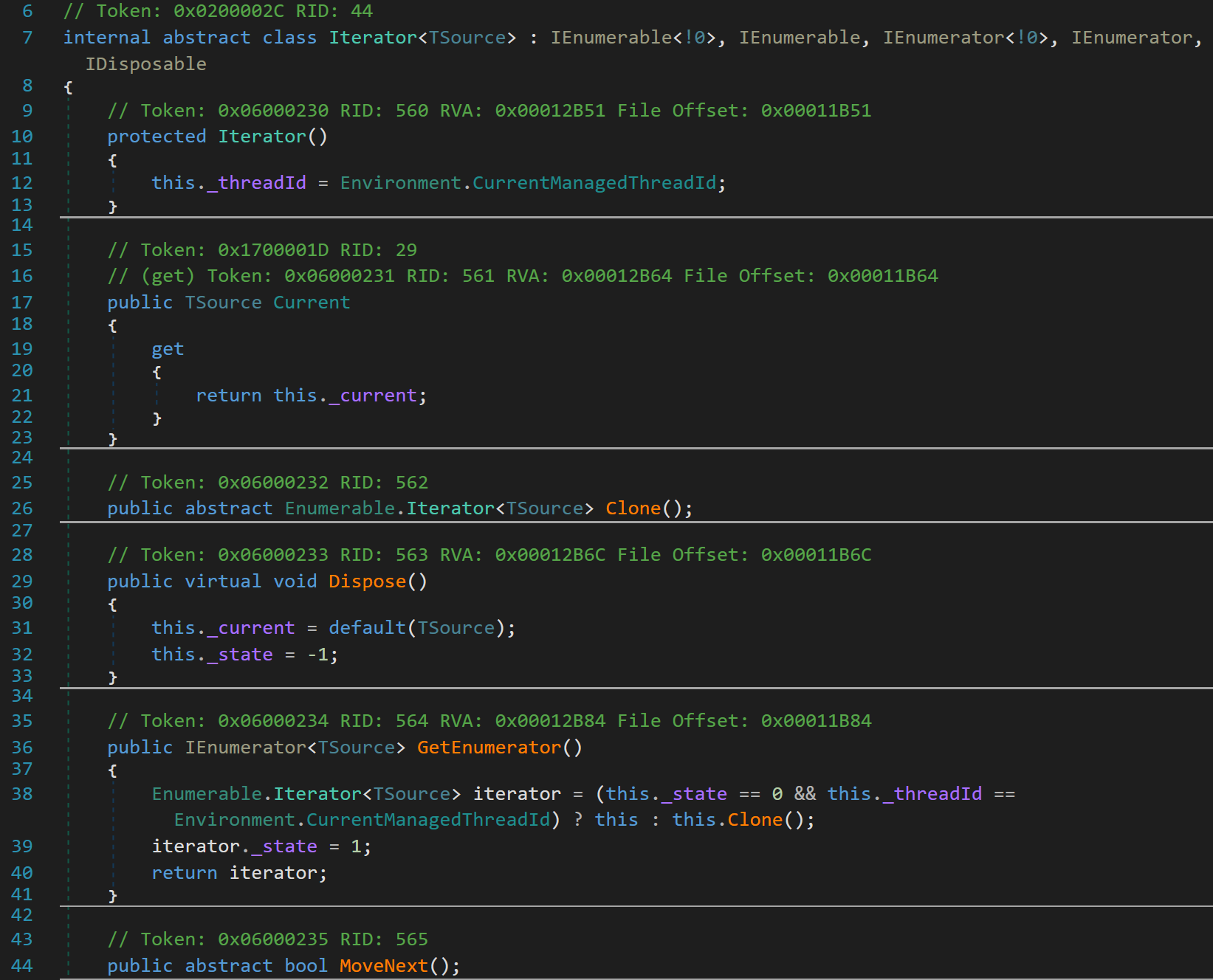
- Line 12:在构造函数内获取当前线程的Id。
- Line 21:Current属性包含一个get访问器(只读),返回当前对象。
- Line 26:该类继承了接口IEnumerable,所以必须实现GetEnumerator()方法。如果当前迭代器的线程Id和当前线程的Id不同,则克隆一个新的迭代器返回,否则返回当前迭代器。
- Line 29:该类继承了接口IDisposable,所以必须实现Dispose()方法。必要情况下释放对象。
- Line 36~40:因为需要进行筛选(迭代器遍历)工作,所以需要定义迭代器,并将其初始状态设置为1,返回当前迭代器。
- Line 44:该方法MoveNext()来自于所继承的接口IEnumerator,其根据不同的容器,有不同的实现(就像刚才提到的List和Array的迭代方式),所以定义为抽象方法。
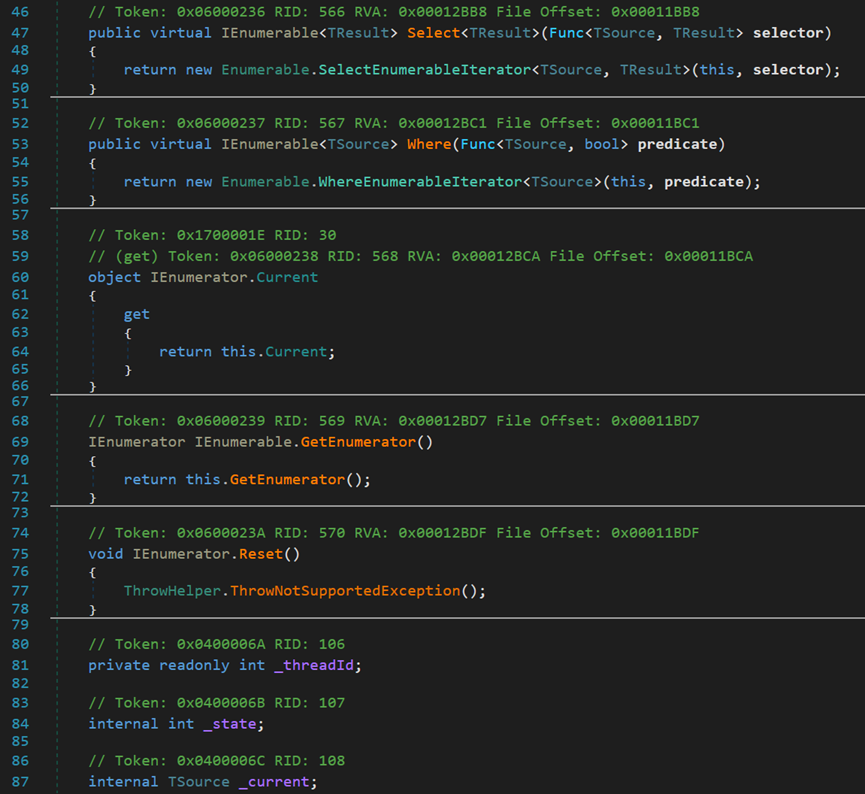
- Line 47~50:虚方法Select(),默认返回WhereEnumerableIterator迭代器。
- Line 53~56:虚方法Where(),默认返回WhereSelectEnumerableIterator迭代器。
这两个迭代器均不参与过滤运算,两个虚方法主要用于具体容器的复用或重写。如果调用Where的迭代器,属于刚才提到的不参与过滤运算的六个迭代器对象,则会覆盖父类中的某些方法;如果是其它迭代器,例如Distinct迭代器,则会调用父类的Where和Select方法。

Where扩展方法(一)

- Line 12~19:检查数据源和过滤器是否为空。
- Line 20:尝试将source转换为迭代器对象,会产生两种情况:
(1)如果是Where相关的迭代器,如调用形式为XX.Where().Where()。此处iterator.Where(predicate)的Iterator是Where相关的迭代器对象(WhereListIterator、WhereArrayIterator),此时调用的Where方法是派生类WhereXXXIterator重写后的Where方法,返回的是WhereXXXIterator对象,XXX表示List或Array或Enumerable。
(2)如果是其他迭代器,如调用形式为XX.Distinct().Where(),此处iterator.Where(predicate)的Iterator是Distinct的迭代器对象,此时调用的Where方法是父类Iterator种的Where方法,返回的是默认的WhereEnumerableIterator对象。
- Line 25~33:尝试将source转换为数组类型。若转换成功且长度不为0,则返回WhereArrayIterator实例。
- Line 34~41:尝试将source转换为List类型。若转换成功且长度不为0,则返回WhereListIterator实例。
- 若两种类型均无法转换,则返回默认实例WhereEnumerableIterator。
Where扩展方法(二)
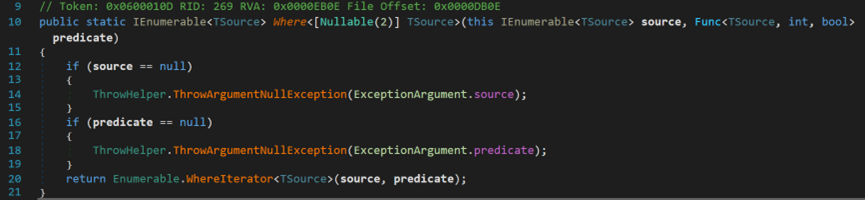
该方法为带索引参数的扩展方法,其没有对线程对资源的占用情况进行检查,而是直接调用了WhereIterator方法
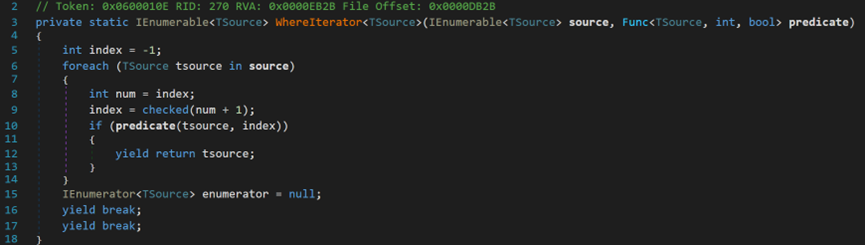
WhereIterator方法中维护了一个计数器,每循环一次,计数器加1,计数器中如果出现整型数字溢出情况,则抛出异常。yield return将结果以值的形式返回给枚举器对象,可一次返回一个元素;yield break将控制权无条件地交给迭代器的调用方,该调用方为枚举器对象的IEnumerator.MoveNext方法(或其对应的泛型System.Collections.Generic.IEnumerable<T>)或Dispose方法。
[# 有关迭代器WhereEnumerableIterator的源码]
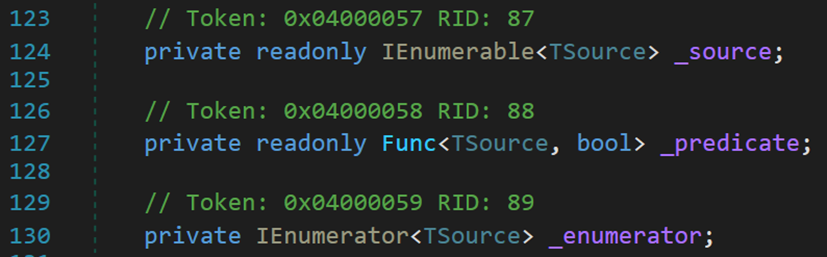
其包含三个字段:源数据、过滤器、迭代器对象。
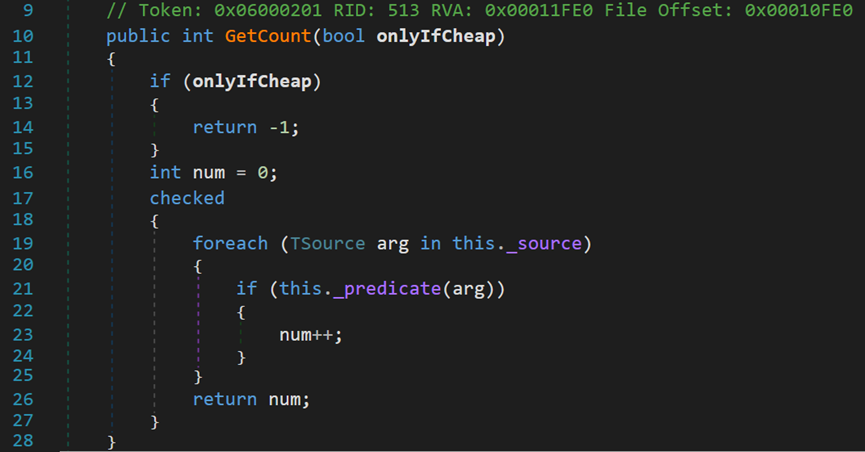
GetCount()方法在上文提到过,用于计算源数据集中,符合条件的元素个数,默认传入true。
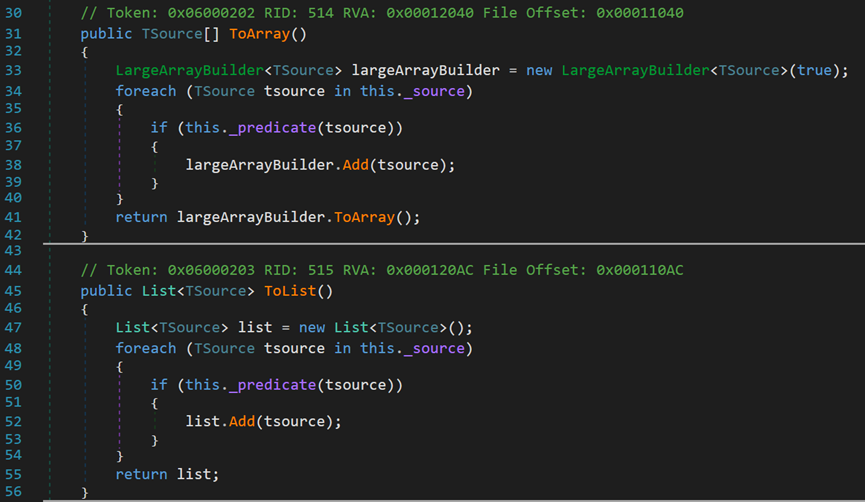
包含两个类型转换方法,分别转换为数组类型和泛型集合类型。转换原理均是通过建立相应对象,并写入数据完成。

一个构造方法,初始化源数据集和过滤器对象。

继承的类与接口。
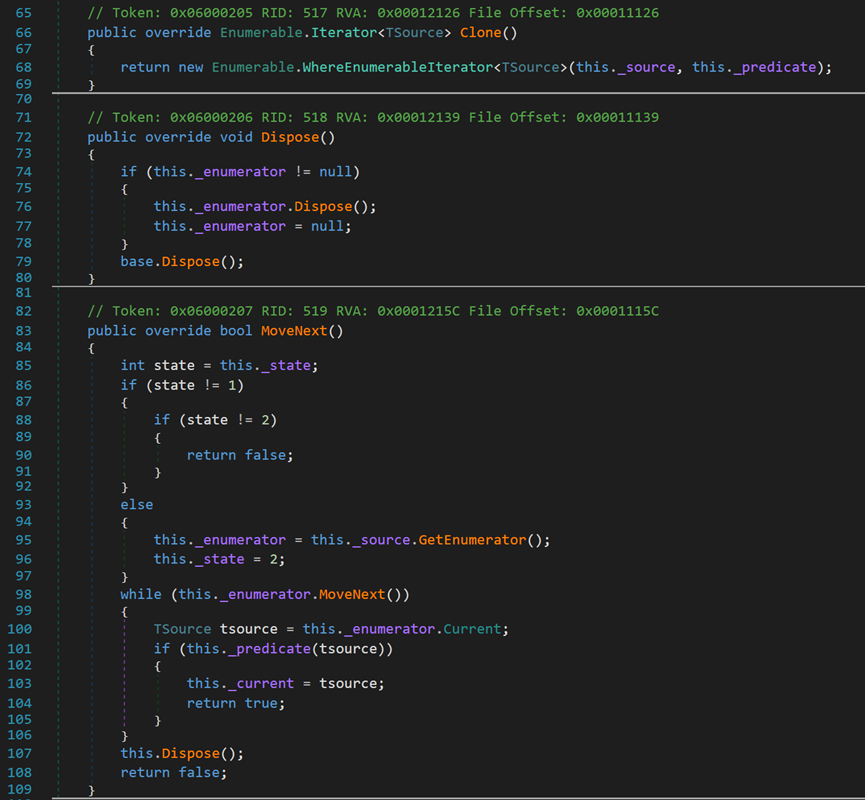
由于其继承了许多接口和类,所以此处重写了接口中的方法,包括创建并返回新的(克隆)迭代器对象、释放对象、向后移动到下一个元素。
- Line 85:变量 _state 位于类Enumerable中的Iterator类型中,初始值为1,用于表示当前状态,指示出下一步应当怎么做。
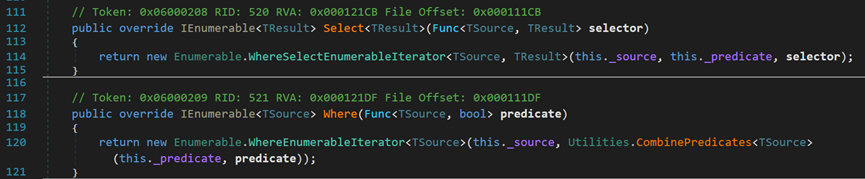
重写了IEnumerable<TSource>接口中的Select()和Where()方法,用于当调用Where的迭代器不属于六大类型时,调用上一级的方法。
【Select()方法和Where()方法原理类似,在此不作叙述】
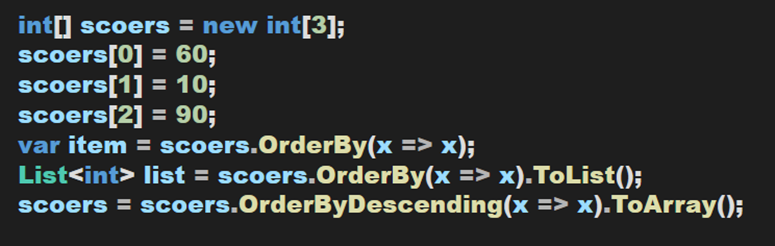
(五)排序
将了这么多题外话,终于拉回了主题。Linq中也有用于排序的方法,包括OrderBy、OrderByDescending、ThenBy、ThenByDescending,在一个语句中,以OrderBy型开头,之后的只能用ThenBy型,但ThenBy型可多次使用。一般地,O/T型共同存在的排序多用于多关键字排序。
基础语法如下:
[# 有关OrderBy的源码]


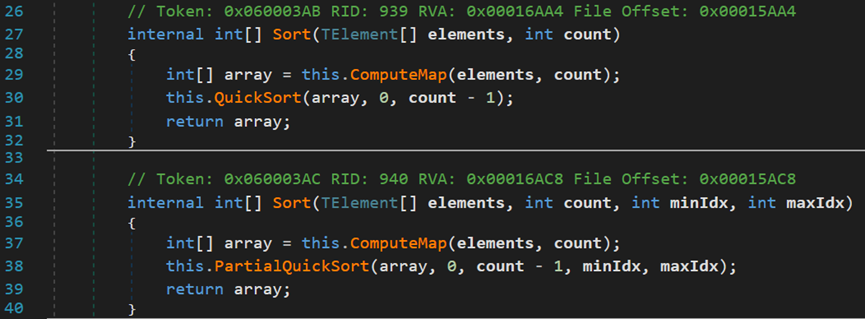
OrderBy()方法有两个重载方法,均返回一个OrderedEnumerable类型的对象。
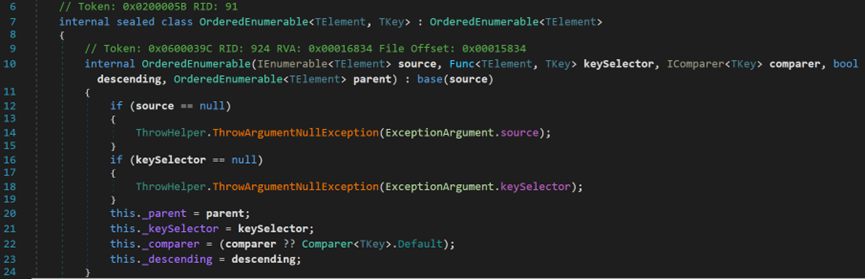
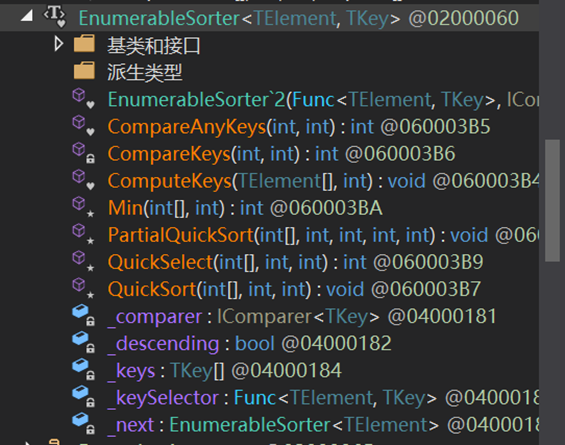
其内置的排序方法,位于类EnumerableSorter<TElement, TKey>中,分别为PartialQuickSort()和QuickSort()。
在排序前,
(1) 对于QuickSort()方法


其重写了父类EnumerableSorter<TElement>中的同名抽象方法,并调用类ArraySortHelper<T>中的IntrospectiveSort()方法,这与前一篇文章中提到的数组排序方法Array.Sort(),方法一致。
(2) 对于PartialQuickSort()方法
该方法直接定义在类EnumerableSorter<TElement, TKey>中,针对源数据集的某一部分进行排序。
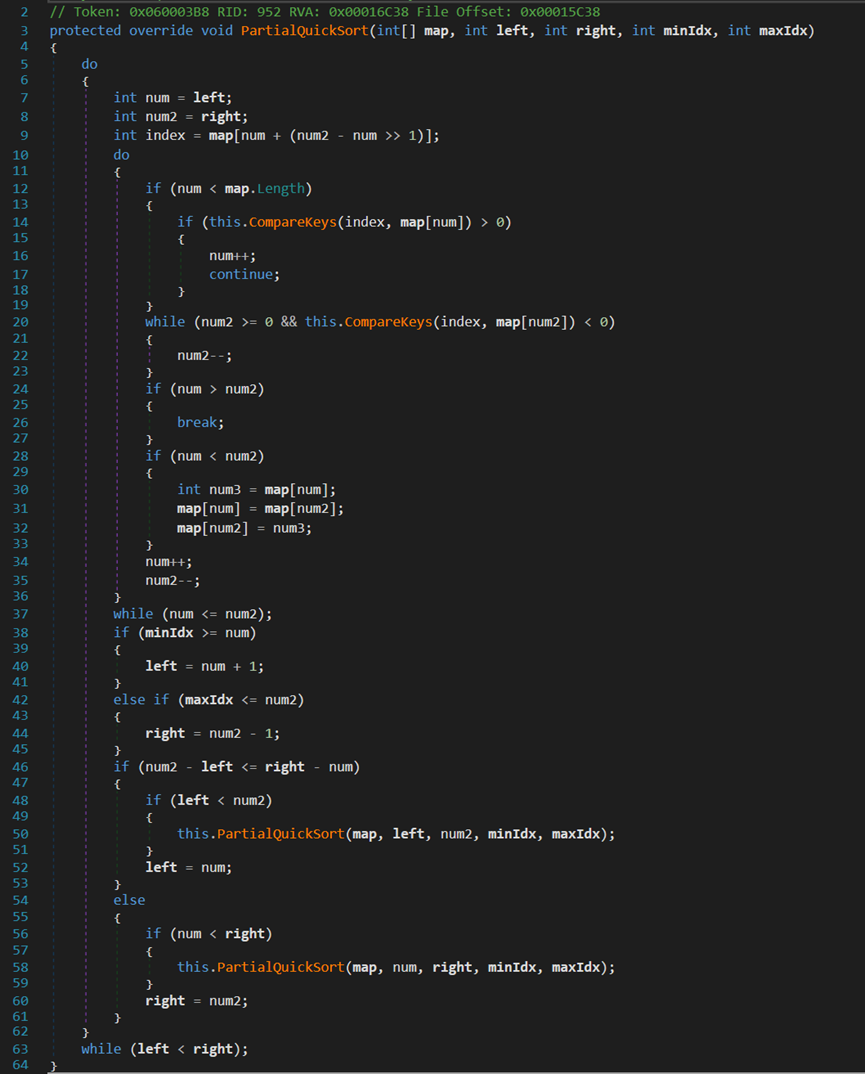
- Line 3:map为待排序数组;letf与right为边界指针(此处的指针有别于C/C++中的指针,此处仅代表一个标记);minIdx与maxIdx为排序区域。
- Line 12~19:当left小于length(未越界)时,CompareKeys()方法用于返回两元素的大小关系:相等返回0,左大右小返回1,反之返回-1。
从左往右,找到第一个大于等于中间位置的元素。
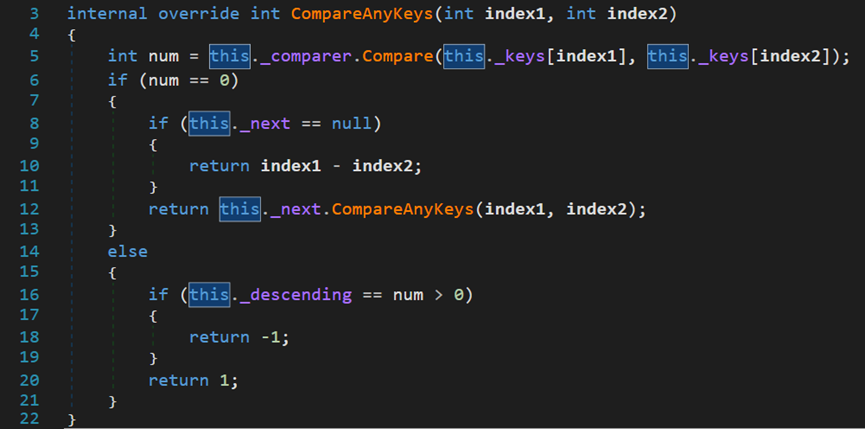
其方法内部的四个紫色字段均在类EnumerableSorter中

【注:下方有关五个参数的解释为推断得出】
_keySelector表示委托方法Func(),过滤器;_compare表示比较器对象;_descending表示是否降序;_next下一个迭代排序器对象;_keys表示经过滤器筛选出的待排序数据集;
- Line 20~23:从右往左,找到第一个小于等于中间位置的元素。
- Line 24~37:如果left与right没有彼此越过对方,则交换位置,并开始下一次查找。
此时,内层循环结束,完成了以中间位置元素为基准值的排序,保证基准值左侧小、右侧大。
- Line 38~45:若此时两指针并未在需求的排序区域内,则相对应方向移动。
- Line 46~61:当内层循环结束时两指针的大小关系为num = num2 + 1,所以Line 46在判断被两指针分割的两部分,哪一部分更短,优选处理短的一部分。
整个排序过程以递归的方式进行,类似于快速排序。
【注:以下内容属于推断得出】

数据集在调用OrderBy()等一类排序方法后,会先将源数据转换为泛型Buffer类型

之后,再调用类OrderedEnumerable中的SortedMap()方法
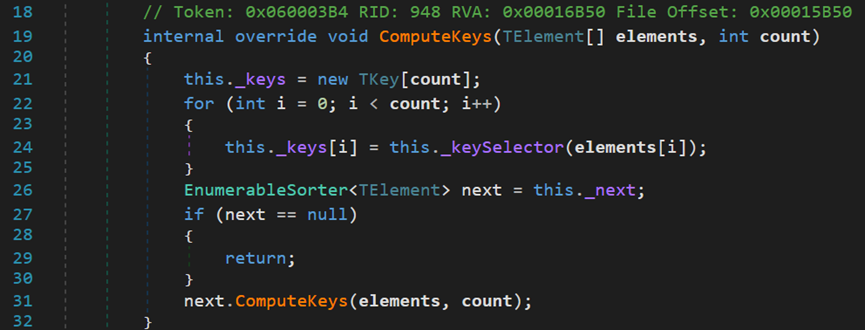
在调用真正开始排序前,首先调用ComputeMap()方法,根据过滤器,筛选出要排序的元素,并保存在_keys中。再根据不同的参数,调用不同的方法进行排序。
以上为OrderBy一类排序方法的“前摇”和过程,其余的OrderByDescenidng()、ThenBy()、ThenByDescending()方法与OrderBy()类似。
流程图如下:

小结二
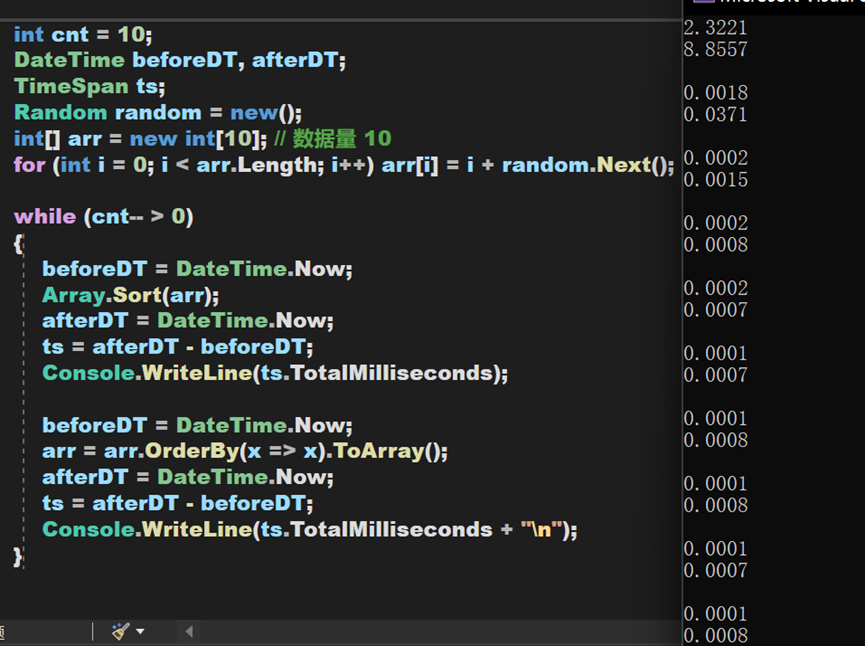
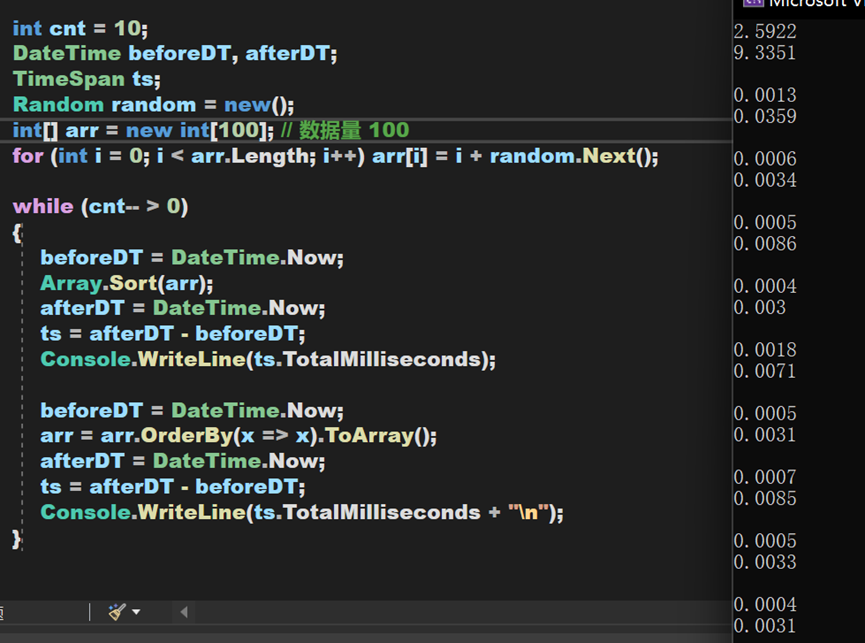
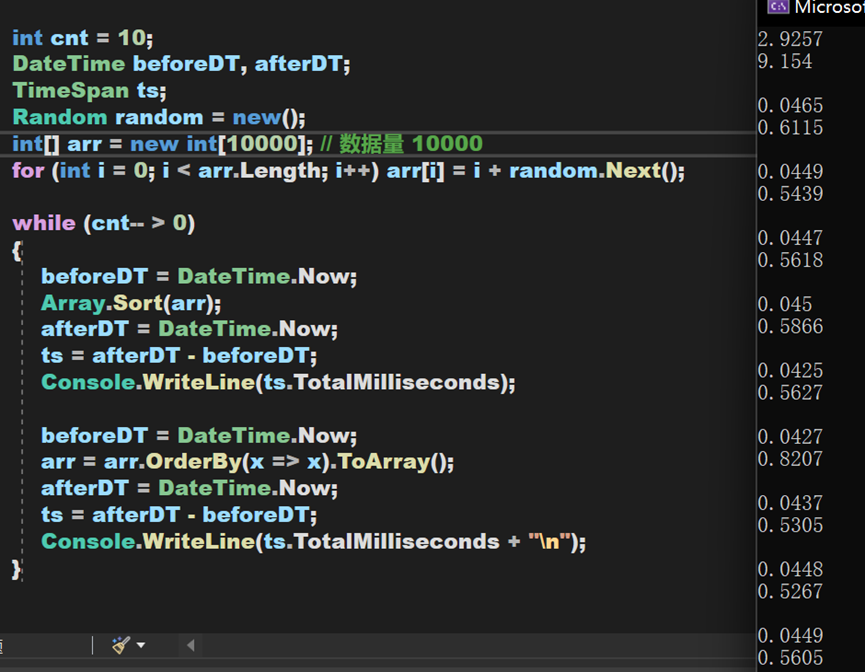
综合来看,就对于OrderBy一类排序算法本身,其时间复杂度和Array中的Sort()方法相差不大,但实际运行效果却要比Array.Sort()方法慢。原因应该在于其需要频繁创建EnumerableSorter对象、将数据类型转换为Buffer再转换为数组、排序后从IOrderByEnumerable类型转换为源数据类型,这些过程大大延长了总时间,尤其是在数据量较大的时候,所需时间将会产生较大差异。
三.有关Lambda表达式
Lambda表达式用来创建匿名函数,常用于委托、回调,且可以访问到外部变量。使用Lambda运算符“=>”,从其主体中分离 lambda 参数列表,可采用以下任意一种形式:
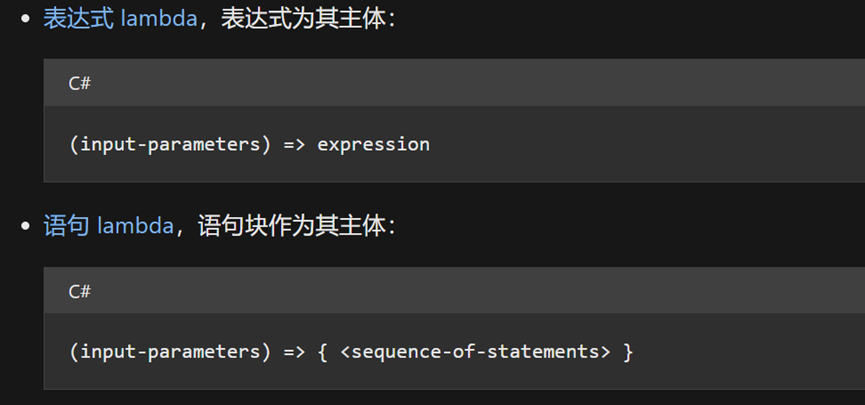
一般地,输入的参数不需要显示指定类型。但当编译器无法判断其类型时,可显示指明各个参数的类型:

(一) 有关匿名
(1)匿名类型
该类型可用来将一组只读属性封装到单个对象中,而无需显式定义一个类型。类型由编译器在编译阶段生成,并且不能在源代码级使用。可结合使用new运算符和对象初始值设定项创建匿名类型。
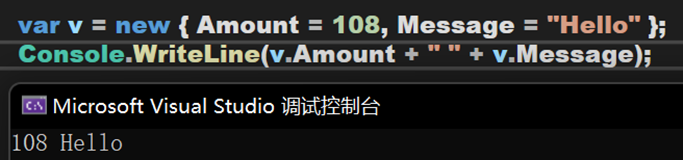


其中,这里的var被定义为匿名类型(AnonymousType),v被定义为类型 `a 。

在反编译程序中,查询到20中相关的方法

根据IL DASM工具可以发现,其包含的主要信息:类<>f__AnonymousType0`2<’<参数para>j__TPar’,’<Message>j__TPar’>;私有只读字段<Amount>i__Field和<Message>i__Field;三个非静态重写方法Equals()、GetHashCode()、ToString()。
以此为例,在源码中找到相关信息,其位于程序集PresentationFramwork.dll中
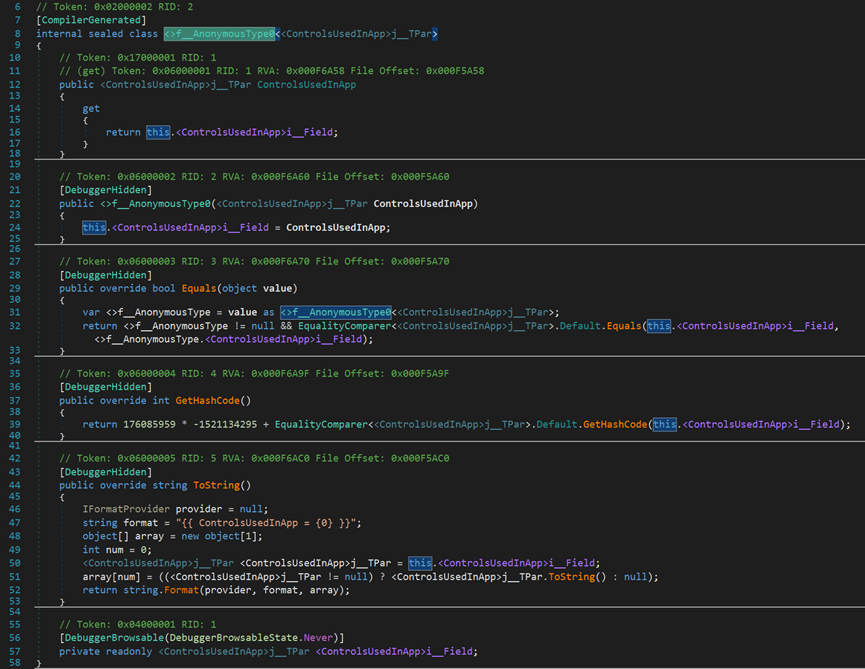
- Line 8:内部密封类,类名为<>f__AnonymousType0;泛型类型为<ControlsUsedInApp>j__TPar。
- Line 12~17:定义参数变量的属性—get(只读)。
- Line 21~25:构造函数,将传入的参数赋值给类的内部变量。
- Line 29~33:Equals()方法,尝试将传入的Object类型对象转换为与被比较对象相同的匿名类型,并按照默认比较其和基本原则,按顺序逐一比较内部参数。
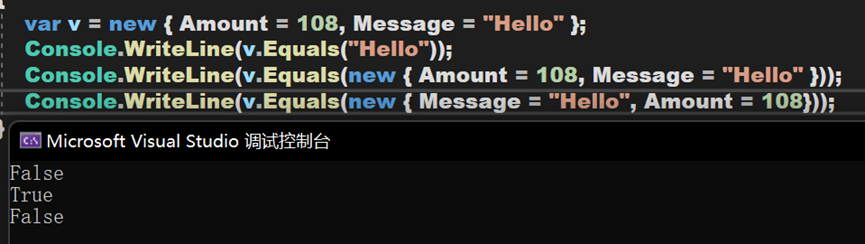
- Line 37~40:返回当前对象的哈希代码。哈希码为每个变量/对象的唯一标识符,用于在一定情况下相互区别。
- Line 44~53:将匿名类型的整个部分转化为字符串的形式(大括号居然也算!?)。
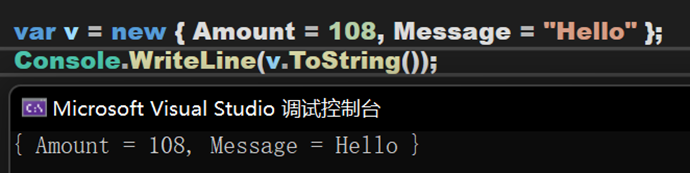
(2)匿名方法
委托是用于引用与其具有相同标签的方法。即,可以使用委托对象调用可由委托引用的方法。匿名方法提供了一种传递代码块作为委托参数的技术,其没有名称只有方法体;没有返回值类型,类型根据具体方法中的return语句推断。如,Func()方法、Action()方法、Predicate()方法。

所以在OrderBy一类排序中,其内部需要传入一个匿名方法,以赋值给Func()方法,故使用Lambda表达式。
(二) Lambda 表达式的自然类型
Lambda表达式本身没有类型,因为CLS(通用类型系统)没有“Lambda 表达式”这一固有概念。不过,有时以非正式的方式谈论 Lambda 表达式的“类型”会很方便。该非正式“类型”是指委托类型或 Lambda 表达式所转换到的Expression类型。
从C# 10开始,Lambda表达式可能具有自然类型。编译器不会强制为 Lambda 表达式声明委托类型(如Func<>或Action<>),而是根据 Lambda 表达式推断委托类型。

也就是说,一开始的Lambda表达式只能赋值给委托类型。而在此之后,Lambda表达式可以根据具体的情况,赋值给具体的类型。
【注:更多Lambda表达式内容请参阅Lambda 表达式 - C# 引用 | Microsoft Docs】
[# 有关泛型的协变与逆变]
据官方解释,协变指能够使用比原始指定的派生类型的派生程度更大(更具体的)的类型;逆变指能够使用比原始指定的派生类型的派生程度更小(不太具体的)的类型。
在谈论协变与逆变之前先来看一下泛型集合中的对象转换。
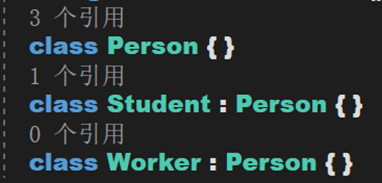
此处有三个类。其中Student与Worker派生自Person,那么可以将Person称为Student和Worker的上层数据类型;Student和Worker称为Person的下层类型。
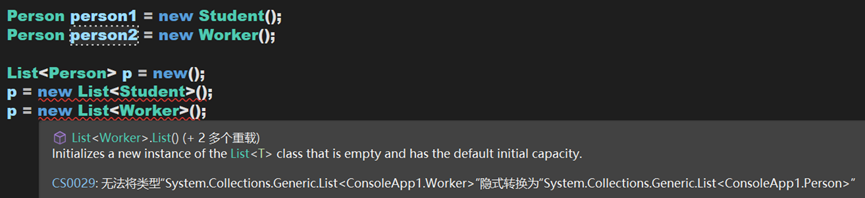
可以发现,虽然Person时Student和Worker的父类,但List<Person>不是List<Student>和List<Worker>的父类,所以后两行的赋值会报错。
在C# 4之前,类似于上述的赋值操作是不被允许的。因为假设其能够赋值,即List<Person> p = new List<Student>();成立,那么虽然p的类型为List<Person>但其实例对象使List<Student>,在调用方法时,调用的也就是Student的方法。如果现在实现这个语句:p.Add(new Person());其实质上是用Student中的Add方法,而Student又是Person的子类,Person无法安全(直接)转换为Studnt对象,所以这样的集合定义没有意义,因此不被允许。
从C# 4开始,类似的操作,在泛型委托、泛型接口中,允许发生。但上述操作依旧是无法实现的,因为其违反类型类型转换的基本流程。
定义一个无参泛型委托。

- 协变:

我们尝试在上层类型中存放下层类型。不出意外,依旧报错。根据刚才的分析,要想解决这个错误,需要解决两个问题:
(1) 在调用p()方法时,实际上调用的是s()方法,所以需要s执行的结果能转换为p执行后所返回的类型。即,s能够转换为p类型。
(2) 解除编译器的检查限制,在此处允许将Work<Student>类型的对象赋值给Work<Person>类型的变量。
对于(1)已经满足,由隐式转换直接完成;而条件(2)就需要在委托中加上out关键字。

- 逆变

尝试在上层类型中存放下层类型。解决这个错误,也需要解决两个问题:
(1)在调用s()方法时,实际上调用的是p()方法,即,p能够转换为s类型。
(2)解除编译器的检查限制,在此处允许将Work<Person>类型的对象赋值给Work<Student>类型的变量。
对于(1)因为Student为Person的子类,所以二者存在联系,通过强制类型转换可以实现;而条件(2)需要在委托中加上in关键字。

【注:如果没有子父类的关系,加上in/out关键字,也无法实现】
简而言之:协变可以在上层数据类型中存放下层对象;逆变可以在下层的数据类型中存放上层对象(这里的上层与下层是相对而言),这两个过程本质上是参数的类型转换。

据微软官方的说法,协变于逆变只发生在数组、委托、泛型参数之上,对于类的上下转型而言不算做协变于逆变。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号