[20180901]四校联考
T1、数列(number)

Solution
首先我们考虑形如\(\frac{n^2}{2}\)的数,显然n个这样的数会提供\(\frac{n(n-1)}{2}\)对。
把k看作是几个形如\(\frac{n(n-1)}{2}\)的和,从大到小贪心加。
要保证任意两个不同的数的和不是完全平方数,暴力构造一下就可以了。
#include<iostream>
#include<cstdio>
#include<algorithm>
typedef long long ll;
ll K,num[100005],a[155];
ll ans,print[155];
ll l,r,res,pos=0;
const ll nn[105]={0,1,3,5,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49,51,53,55,57,59,61,63,65,67};
int main(){
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
scanf("%lld",&K);
if(K<100000){
if(K<=6){
printf("%lld\n",K+1);printf("1 ");
for(int i=1;i<=K;i++) printf("3 ");
}
else{
printf("%d\n",K-1);
printf("2 2 2 2 ");printf("1 ");
for(int i=1;i<=K-6;i++) printf("3 ");
}
return 0;
}
for(int i=1;i<=100000;i++) num[i]=1LL*i*(i-1)/2;
for(int i=1;i<=100;i++) a[i]=2LL*nn[i]*nn[i];
while(K!=0){
++pos;
l=2;r=100000;
while(l<=r){
ll mid=(l+r)>>1;
if(num[mid]<=K) res=mid,l=mid+1;
else r=mid-1;
}
print[pos]=res;
K-=num[res];ans+=res;
}
printf("%lld\n",ans);
for(register int i=1;i<=pos;i++)
for(register int j=1;j<=print[i];j++) printf("%lld ",a[i]);
return 0;
}
T2、散步(walk)

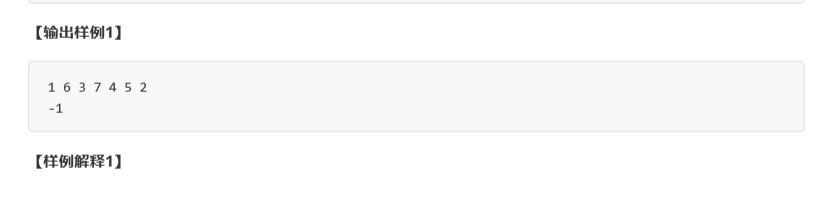
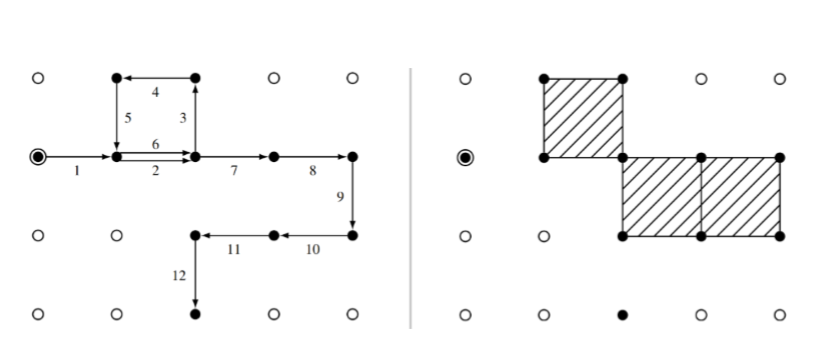

Solution
对于15分,直接用map来记录就可以直接判断了。
官方题解

/*15 points
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<map>
#define MN 100005
using namespace std;
int x,y,n,k,ans;
char s[MN];
std::map<std::pair<int,int>,bool> mp;
std::map<std::pair<int,int>,bool> Mp;
int main(){
freopen("walk.in","r",stdin);
freopen("walk.out","w",stdout);
scanf("%d%d",&n,&k);
scanf("%s",s+1);
if(k!=1) return 0*puts("orz!");
x=0;y=0;mp[make_pair(0,0)]=true;
for(int i=1;i<=n;i++){
if(s[i]=='W'){x-=1;}
if(s[i]=='E'){x+=1;}
if(s[i]=='S'){y-=1;}
if(s[i]=='N'){y+=1;}
mp[make_pair(x,y)]=true;
if(mp[make_pair(x-1,y)]&&mp[make_pair(x-1,y-1)]&&mp[make_pair(x,y-1)]&&Mp[make_pair(x-1,y-1)]!=true) Mp[make_pair(x-1,y-1)]=true,ans++;
if(mp[make_pair(x-1,y)]&&mp[make_pair(x-1,y+1)]&&mp[make_pair(x,y+1)]&&Mp[make_pair(x-1,y)]!=true) Mp[make_pair(x-1,y)]=true,ans++;
if(mp[make_pair(x+1,y)]&&mp[make_pair(x+1,y-1)]&&mp[make_pair(x,y-1)]&&Mp[make_pair(x,y-1)]!=true) Mp[make_pair(x,y-1)]=true,ans++;
if(mp[make_pair(x+1,y)]&&mp[make_pair(x+1,y+1)]&&mp[make_pair(x,y+1)]&&Mp[make_pair(x,y)]!=true) Mp[make_pair(x,y)]=true,ans++;
}
printf("%d\n",ans);
}*/
#include<bits/stdc++.h>
#define ll long long
#define F(i,a,b) for(i=a;i<=b;i++)
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
#define MN 100005
#define depail std::deque<std::pair<int,int> >
#define MAP std::map<std::pair<int,int>,depail >
int n,k,a[MN],b[MN],p,q;
char s[MN];MAP mp;ll ans;
int calc(int tp,depail a,depail b,depail c,depail d){
for(depail::iterator i=a.begin();i!=a.end();i++) i->first+=tp,i->second+=tp;
for(depail::iterator i=b.begin();i!=b.end();i++) i->first+=tp,i->second+=tp;
int res=0;
#define f(a) (a.empty()?-1e9:a.front().second)
#define G(a) a.front().first
#define H(a) if(f(a)==r) a.pop_front();
int l=-1e9;
while(1){
int r=std::min(std::min(f(a),f(b)),std::min(f(c),f(d)));
if(r==-1e9) break;
l=std::max(l,std::max(std::max(G(a),G(b)),std::max(G(c),G(d))));
if(l<=r) res+=r-l+1,l=r+1;
H(a);H(b);H(c);H(d);
}
return res;
}
int main(){
freopen("walk.in","r",stdin);
freopen("walk.out","w",stdout);
scanf("%d%d",&n,&k);
scanf("%s",s+1);
register int i,x=0,y=0;
F(i,1,n){
if(s[i]=='W'){x-=1;}
if(s[i]=='E'){x+=1;}
if(s[i]=='S'){y-=1;}
if(s[i]=='N'){y+=1;}
a[i]=x;b[i]=y;
}
if(a[n]<0) F(i,1,n) a[i]=-a[i];
if(b[n]<0) F(i,1,n) b[i]=-b[i];
if(a[n]==0) F(i,1,n) std::swap(a[i],b[i]);
p=a[n]?a[n]:-1e9;q=b[n];
if(a[n]==0)
F(i,0,n) mp[std::make_pair(a[i],b[i])].push_back(std::make_pair(0,0));
else
F(i,0,n){
int d=a[i]/p;
if(a[i]-p*d<0) d--;
mp[std::make_pair(a[i]-p*d,b[i]-q*d)].push_back(std::make_pair(d,d+k-1));
// x=a[i]%p;y=b[i]-(a[i]/p)*q;
// mp[std::make_pair(x,y)].push_back(std::make_pair(a[i]/p,a[i]/p+k-1));
}
for(MAP::iterator i=mp.begin();i!=mp.end();++i) sort(i->second.begin(),i->second.end());
for(MAP::iterator i=mp.begin();i!=mp.end();++i){
x=i -> first.first,y=i -> first.second;
#define solve(d,p2,p3,p4) {if(mp.count(p2)&&mp.count(p3)&&mp.count(p4)) ans+=calc(d,i->second,mp[p2],mp[p3],mp[p4]);}
if(x!=p-1) solve(0,std::make_pair(x,y+1),std::make_pair(x+1,y),std::make_pair(x+1,y+1))
else solve(1,std::make_pair(x,y+1),std::make_pair(0,y-q),std::make_pair(0,y-q+1))
}
printf("%lld",ans);
return 0;
}
T3、考古(archaeology)

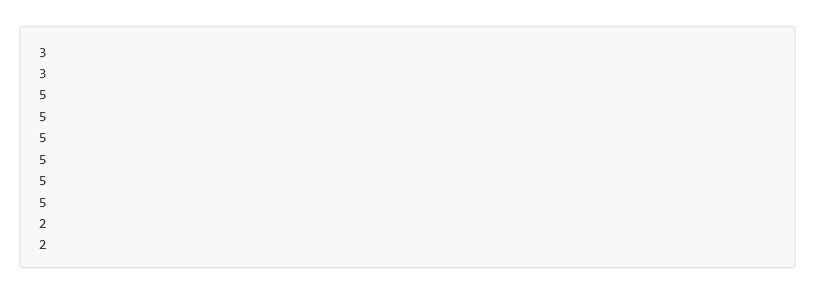
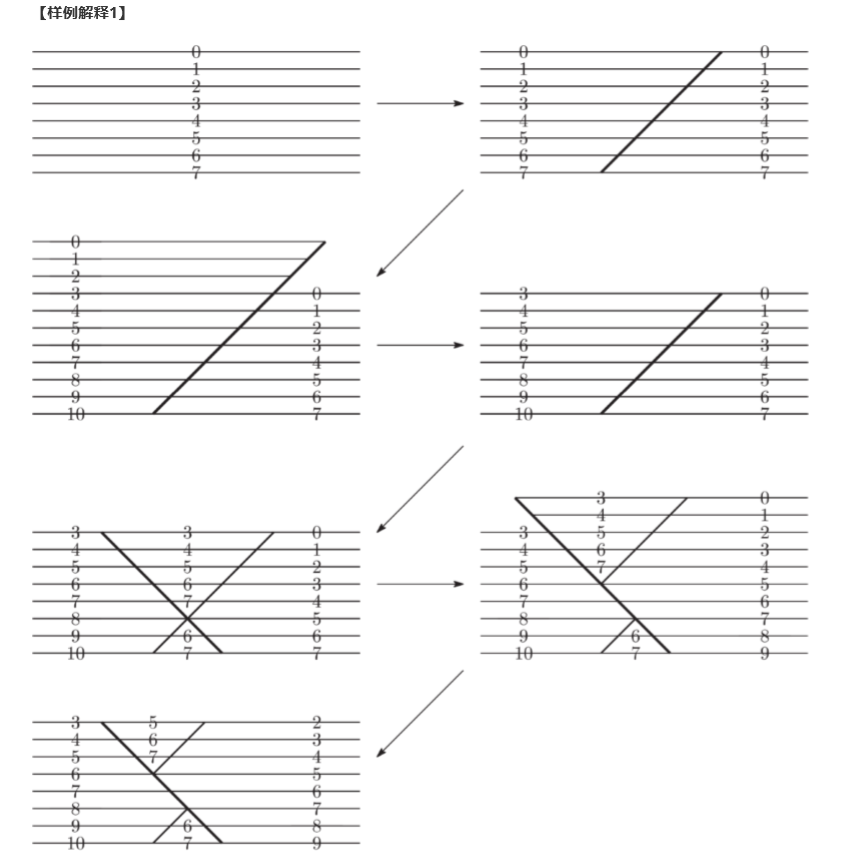

Solution
把操作反过来,就可以看成是,每次会有一段地面下降,问最后每一段地面会降至那一层。
用树状数组/线段树来维护下降过程中每一段的(x,y)值,寻找下降的区间可以直接在树状数组/线段树上二分。
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
#define MN 200005
#define ll long long
#define lowbit(a) (a&-a)
int n,q,x[MN],l[MN];
ll xpos[MN],ypos[MN],pos,X,Y;
bool d[MN];
void Cx(int x,int val){for(;x<=n;x+=lowbit(x))xpos[x]+=val;}
void Cy(int x,int val){for(;x<=n;x+=lowbit(x))ypos[x]+=val;}
ll G(int x){ll res=0;for(;x;x-=lowbit(x)) res+=ypos[x];return res;}
int main(){
freopen("archaeology.in","r",stdin);
freopen("archaeology.out","w",stdout);
n=read();q=read();
register int i,j;
for(i=1;i<=q;++i) x[i]=read(),d[i]=read()==1,l[i]=read();
for(i=2;i<=n;++i) Cx(i,1);
for(i=q;i;--i){
if(d[i]){
pos=X=Y=0;
for(j=17;~j;--j)if((pos|1<<j)<=n&&X+xpos[pos|1<<j]-Y-ypos[pos|1<<j]<x[i]) pos|=1<<j,X+=xpos[pos],Y+=ypos[pos];
Cx(1,-l[i]),Cy(1,-l[i]);
Cx(pos+1,l[i]),Cy(pos+1,l[i]);
}
else{
pos=X=Y=0;
for(j=17;~j;--j)if((pos|1<<j)<=n&&X+xpos[pos|1<<j]+Y+ypos[pos|1<<j]<x[i]) pos|=1<<j,X+=xpos[pos],Y+=ypos[pos];
Cx(pos+1,l[i]),Cy(pos+1,-l[i]);
}
}
for(i=1;i<=n;i++) printf("%lld\n",-G(i));
return 0;
}
Blog来自PaperCloud,未经允许,请勿转载,TKS!!
致虚极,守静笃,万物并作,吾以观其复


 浙公网安备 33010602011771号
浙公网安备 33010602011771号