网络流24题小结
1.飞行员配对方案问题
二分图最大匹配。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 2005 #define S 0 #define T 205 #define inf 200000000 struct edge{int to,w,nex;}e[MN*T]; int hr[T+5],cnt=1,d[T+5]; int q[T+5],top,ans; int m,n; void ins(int f,int t,int w){ e[++cnt]=edge{t,w,hr[f]};hr[f]=cnt; e[++cnt]=edge{f,0,hr[t]};hr[t]=cnt; } bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[top=i=1]=S]=1;i<=top;++i) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f; register int i,used=0; for(i=hr[x];i;i=e[i].nex) if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; if(f==used) return f; } return d[x]=-1,used; } int main(){ n=read(),m=read(); register int x,y; while(1){ x=read(),y=read(); if(x==-1&&y==-1) break; ins(x,y+100,1); } for(x=1;x<=n;x++) ins(S,x,1); for(y=1;y<=m;y++) ins(y+100,T,1); while(bfs()) ans+=dfs(S,inf); printf("%d\n",ans); if(!ans) printf("No Solution!\n"); for(int i=hr[S];i;i=e[i].nex)if(!e[i].w){ for(int j=hr[e[i].to];j;j=e[j].nex)if(!e[j].w&&e[j].to!=S) printf("%d %d\n",e[i].to,e[j].to-100); } return 0; }
2.太空飞行计划问题
最大权闭合图?最小割

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 55 int val[MN],sum; #define S 0 #define T 105 #define inf 200000000 struct edge{int to,w,nex;}e[MN*T]; int hr[T+5],cnt=1,d[T+5]; int q[T+5],top,ans; int m,n; void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[top=i=1]=S]=1;i<=top;++i) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f; int used=0; for(int i=hr[x];i;i=e[i].nex) if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(f-used,e[i].w)); used+=w; e[i].w-=w; e[i^1].w+=w; if(f==used) return f; } return d[x]=-1,used; } int main(){ n=read(),m=read(); register int i,j,ulen,num;char c[10000]; for(i=1;i<=n;i++){ val[i]=read(); ins(S,i,val[i]);sum+=val[i]; memset(c,0,sizeof c); cin.getline(c,10000); ulen=0; while(sscanf(c+ulen,"%d",&num)==1){ ins(i,50+num,inf); if(num==0) ulen++; else while(num) num/=10,ulen++; ulen++; } } for(i=1;i<=m;i++) ins(i+50,T,read()); while(bfs()) ans+=dfs(S,inf); for(i=1;i<=n;i++) if(d[i]>0) printf("%d ",i);puts(""); for(i=1;i<=m;i++) if(d[i+50]>0) printf("%d ",i);puts(""); printf("%d\n",sum-ans); return 0; }
3.最小路径覆盖问题
先拆点,最小路径覆盖=总点数-二分图的最大匹配。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 155 #define ME 15005 #define inf 2000000000 #define S 0 #define T 305 int n,m,ans; struct edge{int to,w,nex;}e[ME*2]; int cnt=1,hr[T+5],d[T+5],q[T+5],top; inline void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[top=i=1]=S]=1;i<=top;i++) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f;int used=0; for(int i=hr[x];i;i=e[i].nex) if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(e[i].w,f-used)); used+=w;e[i].w-=w;e[i^1].w+=w; if(used==f) return used; } return d[x]=-1,used; } bool prin[MN]; inline void pr(int x){printf("%d ",x);prin[x]=1;} void pri(int x){ int i; for(i=hr[x];i;i=e[i].nex)if(e[i].to!=S&&!e[i].w){ pr(e[i].to-150);pri(e[i].to-150); } } int main(){ n=read(),m=read(); int u,v; for(int i=1;i<=n;i++) ins(S,i,1),ins(i+150,T,1); for(int i=1;i<=m;i++){ u=read(),v=read(); ins(u,v+150,1); } while(bfs()) ans+=dfs(S,inf); for(int i=1;i<=n;i++)if(!prin[i]){ pr(i);pri(i); puts(""); } printf("%d\n",n-ans); return 0; }
4.魔术球问题
仍然是最小路径覆盖问题,我们枚举答案,每次都新增一个点,在残量网络上跑最大流,知道最小路径覆盖超过n。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define Mans 1600 #define inf 2000000000 #define S 0 #define T Mans*2 struct edge{int to,w,nex;}e[Mans*Mans*2]; int cnt=1,hr[T+5],d[T+5],q[T+5],top; int cur[T+5]; inline void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[top=i=1]=S]=1;i<=top;i++) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f;int used=0; for(int i=cur[x];i;i=e[i].nex){ cur[x]=i; if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(e[i].w,f-used)); used+=w;e[i].w-=w;e[i^1].w+=w; if(used==f) return used; } } return d[x]=-1,used; } int n,ans; bool insed[Mans+5]; bool is(int x){return sqrt(x)*sqrt(x)==x;} void insw(int x){ insed[x]=1; ins(S,x,1);ins(x+Mans,T,1); for(int i=sqrt(x)+1;i*i<2*x;++i) ins(i*i-x,x+Mans,1); } void reins(int x){ cnt=1;memset(hr,0,sizeof hr); register int i,j; for(i=1;i<=x;i++)for(int j=sqrt(i)+1;j*j<2*i;++j) ins(j*j-i,i+Mans,1); for(i=1;i<=x;i++) ins(S,i,1),ins(i+Mans,T,1); } bool prin[Mans+5]; inline void pr(int x){printf("%d ",x);prin[x]=1;} void pri(int x){ register int i; for(i=hr[x];i;i=e[i].nex)if(e[i].to!=S&&!e[i].w){ pr(e[i].to-Mans);pri(e[i].to-Mans); } } int main(){ n=read(); register int i=1,j; for(j=1;j<=n;j++) for(;i<=Mans;i++){ if(!insed[i]) insw(i); while(bfs()){ memcpy(cur,hr,sizeof(int)*(T+5)); ans+=dfs(S,inf); } if(i-ans>j) break; } printf("%d\n",i-1); reins(i-1); while(bfs()){ memcpy(cur,hr,sizeof(int)*(T+5)); ans+=dfs(S,inf); } for(j=1;j<=i-1;j++)if(!prin[j]){ pr(j);pri(j); puts(""); } return 0; }
5.圆桌问题
还是匹配问题,源点向单位连容量为人数的边,桌子向汇点连容量为桌子大小的边就行了。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MM 150 #define MN 270 #define ME (MM+1)*(MN+1) #define inf 2000000000 #define S 0 #define T 425 int n,m,ans; struct edge{int to,w,nex;}e[ME*2]; int cnt=1,hr[T+5],d[T+5],q[T+5],cur[T+5],top; inline void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[top=i=1]=S]=1;i<=top;i++) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f;int used=0; for(int i=cur[x];i;i=e[i].nex){ cur[x]=i; if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(e[i].w,f-used)); used+=w;e[i].w-=w;e[i^1].w+=w; if(used==f) return used; } } return d[x]=-1,used; } int sm,x; int main(){ m=read(),n=read(); for(int i=1;i<=m;i++) x=read(),sm+=x,ins(S,i,x); for(int j=1;j<=n;j++) x=read(),ins(j+150,T,x); for(int i=1;i<=m;i++)for(int j=1;j<=n;j++) ins(i,j+150,1); while(bfs()){ memcpy(cur,hr,sizeof(int)*(T+5)); ans+=dfs(S,inf); } if(ans<sm){ printf("0\n"); return 0; } printf("1\n"); for(int i=1;i<=m;i++){ for(int j=hr[i];j;j=e[j].nex) if(e[j].to!=S&&!e[j].w) printf("%d ",e[j].to-150); puts(""); } return 0; }
6.最长不下降子序列问题
首先第1问平方dp就行了。dp[i]表示以i结尾的最长不下降子序列的长度。
第2问的话,要使用上一问的dp值,对图进行分层,每层的数向下一层且在自己之后比自己大的数连边连边,然后跑最大流。
第3问,把S到1号点和n号点到T的容量改为inf,再跑最大流。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 505 #define inf2 0x3f #define inf 10000000 #define ME 250000 #define S 0 #define T 1005 int cnt=1,d[T+5],hr[T+5],cur[T+5],q[T+5],top,ans; struct edge{int to,w,nex;}e[ME]; inline void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } inline bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[i=top=1]=S]=1;i<=top;i++) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } inline int dfs(int x,int f){ if(x==T) return f;int used=0; for(int i=cur[x];i;i=e[i].nex){ cur[x]=i; if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(f-used,e[i].w)); e[i].w-=w,used+=w,e[i^1].w+=w; if(used==f) return used; } } return d[x]=-1,used; } inline void dinic(){ while(bfs()){ memcpy(cur,hr,sizeof(int)*(T+5)); ans+=dfs(S,inf); } } int n,a[MN],f[MN],ct; int main(){ n=read(); register int i,j; for(i=1;i<=n;i++)a[i]=read(); for(i=1;i<=n;i++)for(j=1;j<i;j++)if(a[j]<=a[i]) f[i]=max(f[i],f[j]+1); for(i=1;i<=n;i++) ct=max(ct,f[i]); printf("%d\n",ct+1); for(i=1;i<=n;i++){ if(f[i]==0) ins(S,i,1); ins(i,i+500,1); if(f[i]==ct) ins(i+500,T,1); for(j=i+1;j<=n;j++)if(a[j]>=a[i]&&f[j]-f[i]==1) ins(i+500,j,1); } dinic(); printf("%d\n",ans); ins(S,1,inf);ins(1,501,inf); if(f[n]==ct) ins(n,n+500,inf),ins(n+500,T,inf); dinic(); printf("%d\n",ans); return 0; }
7.试题库问题
还是匹配问题。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 1000 #define T 1025 #define S 0 #define inf 200000000 struct edge{int to,w,nex;}e[MN*T]; int hr[T+5],cnt=1,d[T+5]; int q[T+5],top,ans; int k,n; void ins(int f,int t,int w){ e[++cnt]=edge{t,w,hr[f]};hr[f]=cnt; e[++cnt]=edge{f,0,hr[t]};hr[t]=cnt; } bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[top=i=1]=S]=1;i<=top;++i) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f; register int i,used=0; for(i=hr[x];i;i=e[i].nex) if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; if(f==used) return f; } return d[x]=-1,used; } int main(){ k=read(),n=read(); int sm=0,a; for(int i=1;i<=k;i++) a=read(),sm+=a,ins(1000+i,T,a); for(int i=1;i<=n;i++){ ins(S,i,1);a=read(); for(int j=1;j<=a;j++) ins(i,read()+1000,1); } while(bfs()) ans+=dfs(S,inf); if(ans==sm){ for(int i=1;i<=k;i++){ printf("%d:",i); for(int j=hr[1000+i];j;j=e[j].nex) if(e[j].to!=T&&e[j].w) printf(" %d",e[j].to); puts(""); } } else puts("No Solution!"); return 0; }
8.机器人路径规划问题
9.方格取数问题
二分图点权最大独立集。其实就是最小割,先给图黑白染色,分别连向S和T,相邻格子之间连inf的边,格子和S(或T)之间边的容量为格子内正整数的值。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 105 #define T 10005 #define S 0 #define inf 2e9 struct edge{int to,w,nex;}e[MN*T]; int cnt=1,hr[T+5]; inline void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } int d[T+5],q[T+5],ans,top; bool bfs(){ memset(d,0,sizeof d);register int i,j; for(d[q[i=top=1]=S]=1;i<=top;++i) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f; int used=0; for(int i=hr[x];i;i=e[i].nex) if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; if(used==f) return used; } return d[x]=-1,used; } int n,m,sum; int g(int i,int j){return m*(i-1)+j;} int main(){ n=read(),m=read(); register int i,j,x; for(i=1;i<=n;i++)for(j=1;j<=m;j++) x=read(),sum+=x,(i+j)&1?ins(S,g(i,j),x):ins(g(i,j),T,x); for(i=1;i<=n;i++)for(j=1;j<=m;j++) if((i+j)&1){ if(i>1) ins(g(i,j),g(i-1,j),inf); if(i<n) ins(g(i,j),g(i+1,j),inf); if(j>1) ins(g(i,j),g(i,j-1),inf); if(j<m) ins(g(i,j),g(i,j+1),inf); } while(bfs()) ans+=dfs(S,inf); printf("%d\n",sum-ans); return 0; }
10.餐巾计划问题
最小费用最大流
把每天拆成x[i]和y[i],S向每个x[i]连容量inf,费用为p(餐巾价钱)的边,向y[i]连容量为need[i],费用为0的边,y[i]向y[i+1]连容量inf,费用为0的边,表示当日用剩的餐巾可以留到以后去处理,y[i]向x[i+m]连容量为inf,费用为f的边,表示送到快洗部,慢洗部同理。最后,x[i]向T连边容量为need[i],费用为0,这样用来控制最大流合法。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define inf 0x3f3f3f3f #define ME 100005 #define MN 5005 #define T 4005 #define S 0 long long mincost,maxflow; struct edge{int to,w,c,nex;}e[ME];int hr[MN],cnt=1; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } int d[MN],q[ME],l,r; bool inq[MN],vis[MN]; bool spfa(){ memset(d,0x3f,sizeof d); q[l=r=MN]=T;d[T]=0;inq[T]=1; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]>d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]<d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]!=inf; } int flow(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[x]-e[i].c==d[e[i].to]&&e[i].w){ w=flow(e[i].to,min(f-used,e[i].w)); used+=w;mincost+=w*e[i].c; e[i].w-=w,e[i^1].w+=w; if(f==used) return f; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=flow(S,inf); }while(vis[T]); } } int n,need[T+5],p,m,f,N,s; int main(){ n=read(); register int i; for(i=1;i<=n;i++) need[i]=read(); p=read(),m=read(),f=read(),N=read(),s=read(); for(i=1;i<=n;i++) ins(S,i,inf,p),ins(i,T,need[i],0); for(i=1;i<=n;i++) ins(S,i+2000,need[i],0); for(i=1;i<n;i++) ins(i+2000,i+2001,inf,0); for(i=1;i<=n-m;i++) ins(i+2000,i+m,inf,f); for(i=1;i<=n-N;i++) ins(i+2000,i+N,inf,s); solve(); printf("%lld\n",mincost); return 0; }
11.航空路线问题
最大费用最大流。
题目就是要求找出两条不相交的从1号城市到n号城市的路径,考虑每个城市拆点,连边容量为1,费用为1,西边城市向东边城市连边,S向1号城市连容量为2,费用为0的边,然后跑最大费用最大流,和最小费用流的做法相似。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define inf 0x3f3f3f3f #define MN 105 #define T 205 #define S 0 #define ME 90000 int maxflow,mincost; struct edge{int to,w,c,nex;}e[ME];int hr[T+5],cnt=1; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } int d[T+5],q[ME*2+5],l,r; bool inq[T+5],vis[T+5]; bool spfa(){ memset(d,128,sizeof d); q[l=r=ME]=T;d[T]=0;inq[T]=1; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]<d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]>d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]>0; } int flow(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[x]-e[i].c==d[e[i].to]&&e[i].w){ w=flow(e[i].to,min(f-used,e[i].w)); used+=w;mincost+=w*e[i].c; e[i].w-=w,e[i^1].w+=w; if(f==used) return f; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=flow(S,inf); }while(vis[T]); } } int n,m; char city[MN][20]; char st[20],en[20]; int sta,end; int ct=0,print[3][MN]; inline void solve_(int x){ ct++; if(x==n) return; print[ct][1]=x; print[ct][0]=1;int now=x; while(now!=n){ for(int i=hr[now+100];i;i=e[i].nex){ if(e[i].to==n&&!e[i].w) return; if(!e[i].w&&e[i].to<100){ now=print[ct][++print[ct][0]]=e[i].to; break; } } } } bool pd(char a[],char b[]){ int len; if((len=strlen(a))!=strlen(b)) return false; for(int i=0;i<len;i++) if(a[i]!=b[i]) return false; return true; } int main(){ n=read();m=read();register int i,j; for(i=1;i<=n;i++) scanf("%s",city[i]); for(i=1;i<=m;i++){ scanf("%s%s",st,en); for(j=1;j<=n;j++) if(pd(st,city[j])) sta=j; for(j=1;j<=n;j++) if(pd(en,city[j])) end=j; if(sta>end) swap(sta,end); ins(sta+100,end,1+(sta==1&&end==n),1); } for(i=2;i<n;i++) ins(i,i+100,1,1); ins(S,101,2,1),ins(n,T,2,1); solve(); if(maxflow!=2){ printf("No Solution!\n"); return 0; } for(i=hr[101];i;i=e[i].nex) if(!e[i].w) solve_(e[i].to); printf("%d\n",mincost-2>>1); printf("%s\n",city[1]); for(i=1;i<=print[2][0];i++) printf("%s\n",city[print[2][i]]); printf("%s\n",city[n]); for(i=print[1][0];i>=1;i--) printf("%s\n",city[print[1][i]]); printf("%s\n",city[1]); return 0; }
12.软件补丁问题
这是一道最短路径问题,首先,n<=20,状态压缩。然后根据每个补丁的需要,胡乱转移,spfa跑最短路就行了。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 2005 #define inf 0x3f3f3f3f #define INF dp[(1<<20)+5] int n,m,t[MN],f1[MN],f2[MN],d1[MN],d2[MN]; char c1[MN],c2[MN]; queue<int> q; long long dp[(1<<20)+10]; bool in[1<<20]; void init(int x){ register int i; for(i=0;i<n;i++) f1[x]+=(c1[i]=='+')<<i; for(i=0;i<n;i++) f2[x]+=(c1[i]=='-')<<i; for(i=0;i<n;i++) d1[x]+=(c2[i]=='-')<<i; for(i=0;i<n;i++) d2[x]+=(c2[i]=='+')<<i; } bool pd(int x,int y){ //x>f1[y]&&Cx>f2[y] for(int i=0;i<n;i++){ if((f1[y]>>i)&1&&~(x>>i)&1) return false; if((f2[y]>>i)&1&&(x>>i)&1) return false; } return true; } int change(int x,int y,int z){ for(int i=0;i<n;i++){ if((y>>i)&1&& (x>>i)&1) x-=1<<i; if((z>>i)&1&&~(x>>i)&1) x+=1<<i; } return x; } inline void bfs(){ memset(dp,inf,sizeof dp); dp[(1<<n)-1]=0;q.push((1<<n)-1),in[(1<<n)-1]=1; int xf; while(!q.empty()){ int tp=q.front();q.pop();in[tp]=0; for(int i=1;i<=m;i++){ if(pd(tp,i)&&dp[xf=change(tp,d1[i],d2[i])]>dp[tp]+t[i]){ if(!in[xf])q.push(xf),in[xf]=1;dp[xf]=dp[tp]+t[i]; } } } } int main(){ n=read(),m=read(); register int i,j; for(i=1;i<=m;i++){ scanf("%d%s%s",&t[i],c1,c2); init(i); } bfs(); printf("%d\n",dp[0]==INF?0:dp[0]); return 0; }
13.星际转移问题([CTSC1999]家园)
首先,先用并查集判断一下起点和终点是否相连,然后开始枚举答案,每次t++就增加一组状态点,及飞船i在t时刻的状态,然后从t-1的状态点向t的状态连边,容量为飞船船的载客量,如果当前飞船在0号点,则S向它直接连一条容量为载客量的边,如果在终点,则直接向T连边。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define S 0 #define MN 105 #define ME 1000005 #define inf 0x3f3f3f3f #define T ME-2 struct edge{int to,w,nex;}e[ME]; int cnt=1,hr[T+5],cur[T+5]; int d[T+5],q[T+5],top,ans; int fa[MN],val[MN]; int getf(int x){return x==fa[x]?fa[x]:fa[x]=getf(fa[x]);} void union_(int x,int y){ x=getf(x),y=getf(y); if(x==y) return; fa[x]=y;return; } inline void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[top=i=1]=S]=1;i<=top;i++) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } int dfs(int x,int f){ if(x==T) return f;int used=0; for(int i=cur[x];i;i=e[i].nex){ cur[x]=i; if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(e[i].w,f-used)); used+=w;e[i].w-=w;e[i^1].w+=w; if(used==f) return used; } } return d[x]=-1,used; } void dinic(){ while(bfs()){ memcpy(cur,hr,sizeof(int)*(T+5)); ans+=dfs(S,inf); } } int n,m,k,p[MN],v[MN][MN]; int g(int x,int y){ if(x==0) return y; return x; } inline int solve(){ register int j,i,x,y; for(j=1;;++j){ ins(S,(j-1)*(n+1)+n+1,inf); for(i=1;i<=m;++i){ x=(j-1)%val[i],y=j%val[i]; if(v[i][x]==n+2) x=T; else x=(j-1)*(n+1)+v[i][x]; if(v[i][y]==n+2) y=T; else y=j*(n+1)+v[i][y]; ins(x,y,p[i]); } dinic(); if(ans>=k) return j; for(i=1;i<=n+1;++i) ins((j-1)*(n+1)+i,j*(n+1)+i,inf); } } int main(){ n=read();m=read();k=read(); register int i,j; for(i=1;i<=n+2;i++) fa[i]=i; for(i=1;i<=m;++i){ p[i]=read(),val[i]=read(); for(j=0;j<val[i];++j){ v[i][j]=read(); if(v[i][j]==0) v[i][j]=n+1; if(v[i][j]==-1) v[i][j]=n+2; if(j!=0) union_(v[i][j-1],v[i][j]); } } if(getf(n+1)!=getf(n+2)){puts("0");return 0;} printf("%d\n",solve()); return 0; }
14.孤岛营救问题
最短路问题~f[i][j][k]表示到达(i,j)时手中的钥匙状态为k的最小步数,然后随便转移就行了,实现的话直接广搜会更方便。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 15 int n,m,p,K; int border[MN][MN][MN][MN],zz[MN][MN]; bool vis[MN][MN][1<<10+5]; struct zt{int x,y,z,st;}; const int xx[4]={0,1,0,-1},yy[4]={1,0,-1,0}; queue<zt> q; int main(){ n=read(),m=read(),p=read();K=read(); register int i,j; int a,b,c,d,key,X,Y,step,t; for(i=1;i<=K;i++){ a=read(),b=read(),c=read(),d=read(),key=read(); if(key!=0) border[a][b][c][d]|=1<<key-1,border[c][d][a][b]|=1<<key-1; else border[a][b][c][d]|=1<<p,border[c][d][a][b]|=1<<p; } K=read(); for(i=1;i<=K;i++){ a=read(),b=read(),key=read(); zz[a][b]|=1<<key-1; } q.push((zt){1,1,zz[1][1],0});vis[1][1][zz[1][1]]=1; while(!q.empty()){ zt tp=q.front();q.pop();step=tp.st; // printf("%d %d %d,%d\n",tp.x,tp.y,tp.z,tp.st); if(tp.x==n&&tp.y==m){ printf("%d\n",step); return 0; } for(i=0;i<4;i++){ X=tp.x+xx[i],Y=tp.y+yy[i]; if(X<1||Y<1||X>n||Y>m) continue; t=border[tp.x][tp.y][X][Y]; if((tp.z&t)!=t) continue; if(vis[X][Y][tp.z|zz[X][Y]]) continue; vis[X][Y][tp.z|zz[X][Y]]=1; q.push((zt){X,Y,tp.z|zz[X][Y],step+1}); } } printf("-1\n"); return 0; }
15.汽车加油行驶问题
依旧时最短路~f[i][j][k]表示到达(i,j)时油量为k的最小步数。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } const int xx[4]={-1,0,1,0},yy[4]={0,1,0,-1}; int n,k,a,b,c,ans=99999999; bool mp[105][105],inq[105][105][15]; int f[105][105][14]; struct nd{int x,y,z;}; queue<nd>q; //#define ju [tp.x][tp.y][tp.z] //#define uj [tp.x][tp.y][k] int main(){ n=read(),k=read(),a=read(),b=read(),c=read(); register int i,j; for(i=1;i<=n;i++)for(j=1;j<=n;j++)mp[i][j]=(read()==1); memset(f,127,sizeof f); f[1][1][k]=0;inq[1][1][k]=1;q.push((nd){1,1,k}); while(!q.empty()){ nd tp=q.front();q.pop();inq[tp.x][tp.y][tp.z]=0; if(mp[tp.x][tp.y]&&tp.z!=k){ if(f[tp.x][tp.y][k]>f[tp.x][tp.y][tp.z]+a){ f[tp.x][tp.y][k]=f[tp.x][tp.y][tp.z]+a; if(!inq[tp.x][tp.y][k])inq[tp.x][tp.y][k]=1,q.push((nd){tp.x,tp.y,k}); } continue; } if(f[tp.x][tp.y][k]>f[tp.x][tp.y][tp.z]+a+c){ f[tp.x][tp.y][k]=f[tp.x][tp.y][tp.z]+a+c; if(!inq[tp.x][tp.y][k]) inq[tp.x][tp.y][k]=1,q.push((nd){tp.x,tp.y,k}); } if(tp.z>0)for(i=0;i<4;++i){ int nx=tp.x+xx[i],ny=tp.y+yy[i]; if(nx<1||nx>n||ny<1||ny>n) continue; int ins=(xx[i]<0||yy[i]<0)?b:0; if(f[nx][ny][tp.z-1]>f[tp.x][tp.y][tp.z]+ins){ f[nx][ny][tp.z-1]=f[tp.x][tp.y][tp.z]+ins; if(!inq[nx][ny][tp.z-1]) inq[nx][ny][tp.z-1]=1,q.push((nd){nx,ny,tp.z-1}); } } } for(i=0;i<=k;++i) ans=min(ans,f[n][n][i]); printf("%d\n",ans); }
16.数字梯形问题
拆点,控制点的流量,连边,控制边的流量,同时费用为1,跑最大费用最大流,OK。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 45 #define ME 30000 #define S 0 #define T 1005 #define T1 1004 #define inf 0x3f3f3f3f int mincost,maxflow; struct edge{int to,w,c,nex;}e[ME+5]; int cnt=1,l,u,r,d[T+5],inq[T+5],vis[T+5],q[ME*2+5],hr[T+5]; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } inline bool spfa(){ memset(d,128,sizeof d); q[l=r=ME+1]=T;inq[T]=1;d[T]=0; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]<d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]>d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]>d[1003]; } inline int mcf(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[e[i].to]==d[x]-e[i].c&&e[i].w){ w=mcf(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; mincost+=e[i].c*w; if(f==used) return used; } return used; } inline void solve(){ while(spfa()){ // for(int i=0;i<=20;i++) printf("%d ",d[i]);puts(""); do{ memset(vis,0,sizeof vis); maxflow+=mcf(S,inf); }while(vis[T]); } } int n,m,num[MN][MN],mun[MN][MN],cc; int main(){ m=read(),n=read(); register int i,j; for(i=1;i<=n;++i)for(j=1;j<=m+i-1;++j) num[i][j]=++cc; for(i=1;i<=n;++i)for(j=1;j<=m+i-1;++j) mun[i][j]=read(); for(i=1;i<=m;++i) ins(S,num[1][i],1,0); for(i=1;i<=n;++i)for(j=1;j<=m+i-1;++j)ins(num[i][j],num[i][j]+cc,1,0); for(i=1;i<=n+m-1;++i) ins(num[n][i]+cc,T1,1,mun[n][i]); for(i=1;i<n;++i)for(j=1;j<=i+m-1;++j){ ins(num[i][j]+cc,num[i+1][j],1,mun[i][j]); ins(num[i][j]+cc,num[i+1][j+1],1,mun[i][j]); }ins(T1,T,m,0); solve(); printf("%d\n",mincost); memset(hr,0,sizeof(hr));cnt=1;mincost=maxflow=0; for(i=1;i<=m;++i) ins(S,num[1][i],1,0); for(i=1;i<=n+m-1;++i) ins(num[n][i],T1,inf,mun[n][i]); for(i=1;i<n;++i) for(j=1;j<=m+i-1;++j) ins(num[i][j],num[i+1][j],1,mun[i][j]), ins(num[i][j],num[i+1][j+1],1,mun[i][j]); ins(T1,T,m,0); solve(); printf("%d\n",mincost); memset(hr,0,sizeof(hr));cnt=1;mincost=maxflow=0; for(i=1;i<=m;++i) ins(S,num[1][i],1,0); for(i=1;i<=n+m-1;++i) ins(num[n][i],T1,inf,mun[n][i]); for(i=1;i<n;++i) for(j=1;j<=m+i-1;++j) ins(num[i][j],num[i+1][j],inf,mun[i][j]), ins(num[i][j],num[i+1][j+1],inf,mun[i][j]); ins(T1,T,m,0); solve(); printf("%d\n",mincost); return 0; }
17.运输问题
费用流裸题。最大费用+最小费用。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 105 #define ME 20500 #define S 0 #define T 205 #define inf 0x3f3f3f3f int maxflow,mincost; struct edge{int to,w,c,nex;}e[ME];int hr[T+5],cnt=1; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } int d[T+5],q[ME*2+5],l,r; bool inq[T+5],vis[T+5]; bool spfa(){ memset(d,0x3f,sizeof d); q[l=r=ME]=T;d[T]=0;inq[T]=1; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]>d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]<d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]!=inf; } int flow(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[x]-e[i].c==d[e[i].to]&&e[i].w){ w=flow(e[i].to,min(f-used,e[i].w)); used+=w;mincost+=w*e[i].c; e[i].w-=w,e[i^1].w+=w; if(f==used) return f; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=flow(S,inf); }while(vis[T]); } } int n,m,a[MN],b[MN],cost[MN][MN],maxx; int main(){ n=read();m=read(); register int i,j; for(i=1;i<=n;i++) a[i]=read(); for(i=1;i<=m;i++) b[i]=read(); for(i=1;i<=n;i++)for(j=1;j<=m;j++) cost[i][j]=read(); for(i=1;i<=n;i++) ins(S,i,a[i],0); for(i=1;i<=m;i++) ins(i+n,T,b[i],0); for(i=1;i<=n;i++)for(j=1;j<=m;j++) ins(i,j+n,inf,cost[i][j]); solve(); printf("%d\n",mincost); cnt=1;memset(hr,0,sizeof hr); mincost=maxflow=0; for(i=1;i<=n;i++) ins(S,i,a[i],0); for(i=1;i<=m;i++) ins(i+n,T,b[i],0); for(i=1;i<=n;i++)for(j=1;j<=m;j++) ins(i,j+n,inf,-cost[i][j]); solve(); printf("%d\n",-mincost); return 0; }
18.分配问题
二分图最佳匹配?只会大最小费用最大流。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 105 #define ME 20500 #define S 0 #define T 205 #define inf 0x3f3f3f3f int maxflow,mincost; struct edge{int to,w,c,nex;}e[ME];int hr[T+5],cnt=1; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } int d[T+5],q[ME*2+5],l,r; bool inq[T+5],vis[T+5]; bool spfa(){ memset(d,0x3f,sizeof d); q[l=r=ME]=T;d[T]=0;inq[T]=1; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]>d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]<d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]!=inf; } int flow(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[x]-e[i].c==d[e[i].to]&&e[i].w){ w=flow(e[i].to,min(f-used,e[i].w)); used+=w;mincost+=w*e[i].c; e[i].w-=w,e[i^1].w+=w; if(f==used) return f; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=flow(S,inf); }while(vis[T]); } } int n,cost[MN][MN],maxx; int main(){ n=read(); register int i,j; for(i=1;i<=n;i++)for(j=1;j<=n;j++) cost[i][j]=read(),maxx=max(maxx,cost[i][j]); for(i=1;i<=n;i++) ins(S,i,1,0); for(i=1;i<=n;i++) ins(i+n,T,1,0); for(i=1;i<=n;i++)for(j=1;j<=n;j++) ins(i,j+n,1,cost[i][j]); solve(); printf("%d\n",mincost); cnt=1;memset(hr,0,sizeof hr); mincost=maxflow=0; for(i=1;i<=n;i++) ins(S,i,1,0); for(i=1;i<=n;i++) ins(i+n,T,1,0); for(i=1;i<=n;i++)for(j=1;j<=n;j++) ins(i,j+n,1,maxx-cost[i][j]); solve(); printf("%d\n",maxx*n-mincost); return 0; }
19.负载平衡问题
所有相邻仓库之间连容量inf,费用为1的边,S向所有仓库连容量为库存数量,费用为0的边,所有仓库向T连容量为平均数,费用为0的边。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 105 #define ME 1500 #define S 0 #define T 105 #define inf 0x3f3f3f3f int maxflow,mincost; struct edge{int to,w,c,nex;}e[ME];int hr[T+5],cnt=1; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } int d[T+5],q[ME*2+5],l,r; bool inq[T+5],vis[T+5]; bool spfa(){ memset(d,0x3f,sizeof d); q[l=r=ME]=T;d[T]=0;inq[T]=1; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]>d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]<d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]!=inf; } int flow(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[x]-e[i].c==d[e[i].to]&&e[i].w){ w=flow(e[i].to,min(f-used,e[i].w)); used+=w;mincost+=w*e[i].c; e[i].w-=w,e[i^1].w+=w; if(f==used) return f; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=flow(S,inf); }while(vis[T]); } } int n,num[MN],sum; int main(){ n=read();register int i; for(i=1;i<=n;i++) num[i]=read(),sum+=num[i]; sum/=n; for(i=1;i<=n;i++) ins(S,i,num[i],0),ins(i,T,sum,0); for(i=1;i<=n;i++) ins(i,i+1>n?1:i+1,inf,1),ins(i,i-1<1?n:i-1,inf,1); solve(); printf("%d\n",mincost); return 0; }
20.深海机器人问题
最大费用最大流,有生物标本的点需要拆点,然后连费用为1,流量为1的边就行了。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 16 #define ME 20000 #define S 400 #define T 405 #define inf 200000000 int mincost,maxflow; struct edge{int to,w,c,nex;}e[ME+5]; int hr[T+5],q[ME*2+5],d[T+5],vis[T+5],inq[T+5],cnt=1,l,r,u; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } inline bool spfa(){ memset(d,128,sizeof d); q[l=r=ME+1]=T;inq[T]=1;d[T]=0; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]<d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]>d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]>d[403]; } inline int mcf(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[e[i].to]==d[x]-e[i].c&&e[i].w){ w=mcf(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; mincost+=e[i].c*w; if(f==used) return used; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=mcf(S,inf); }while(vis[T]); } } int a,b,P,Q; inline int pos(int x,int y){return (Q+1)*x+y;} int main(){ a=read(),b=read(),P=read(),Q=read(); register int i,j,x,y,k; for(i=0;i<=P;i++)for(j=1;j<=Q;j++) ins(pos(i,j-1),pos(i,j),1,read()),ins(pos(i,j-1),pos(i,j),inf,0); for(j=0;j<=Q;j++)for(i=1;i<=P;i++) ins(pos(i-1,j),pos(i,j),1,read()),ins(pos(i-1,j),pos(i,j),inf,0); for(i=1;i<=a;i++)k=read(),x=read(),y=read(),ins(S,pos(x,y),k,0); for(i=1;i<=b;i++)k=read(),x=read(),y=read(),ins(pos(x,y),T,k,0); solve(); printf("%d\n",mincost); return 0; }
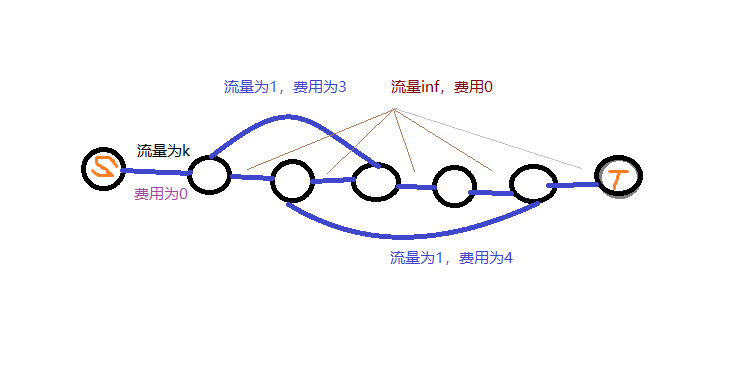
21.最长k可重区间集问题
建图方式:
然后跑最大费用最大流。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define T 1005 #define S 0 #define ME 5000 #define inf 200000000 int mincost,maxflow; struct edge{int to,w,c,nex;}e[ME+5]; int cnt=1,l,u,r,d[T+5],inq[T+5],vis[T+5],q[ME*2+5],hr[T+5]; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } inline bool spfa(){ memset(d,128,sizeof d); q[l=r=ME+1]=T;inq[T]=1;d[T]=0; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]<d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]>d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]>d[1003]; } inline int mcf(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[e[i].to]==d[x]-e[i].c&&e[i].w){ w=mcf(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; mincost+=e[i].c*w; if(f==used) return used; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=mcf(S,inf); }while(vis[T]); } } int n,k; int nd[T+5],rk[T+5],pos[T+5]; bool cmp(int a,int b){return nd[a]<nd[b];} int main(){ n=read(),k=read(); for(int i=1;i<=n;i++)nd[i*2-2]=read(),nd[i*2-1]=read(); for(int i=0;i<n+n;i++) rk[i]=i; sort(rk,rk+n*2,cmp); int now=1;pos[rk[0]]=1; for(int i=1;i<n+n;i++){ if(nd[rk[i]]!=nd[rk[i-1]]) now++; pos[rk[i]]=now; } // for(int i=0;i<n+n;i++) printf("%d ",pos[i]);puts(""); ins(S,1,k,0); for(int i=1;i<now;i++) ins(i,i+1,inf,0); ins(now,T,inf,0); for(int i=0;i<n+n;i+=2) ins(pos[i],pos[i+1],1,nd[i+1]-nd[i]); solve(); printf("%d\n",mincost); return 0; }
22.最长k可重线段集问题
和第21题类似。
由于线段可能垂直于x轴,导致首尾两点作对的x坐标相等,所以我们需要拆点一下。

#include<bits/stdc++.h> using namespace std; inline long long read(){ long long x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define T 2005 #define S 0 #define ME 100000 #define inf 200000000 #define int long long int mincost,maxflow; struct edge{int to,w,c,nex;}e[ME+5]; int cnt=1,l,u,r,d[T+5],inq[T+5],vis[T+5],q[ME*2+5],hr[T+5]; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } inline bool spfa(){ memset(d,128,sizeof d); q[l=r=ME+1]=T;inq[T]=1;d[T]=0; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]<d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]>d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]>d[2003]; } inline int mcf(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[e[i].to]==d[x]-e[i].c&&e[i].w){ w=mcf(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; mincost+=e[i].c*w; if(f==used) return used; } return used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=mcf(S,inf); }while(vis[T]); } } int n,k; int nd[T+5],ndy[T+5],rk[T+5],pos[T+5]; bool cmp(int a,int b){return nd[a]<nd[b];} inline int len(int i){ return floor(sqrt((nd[i]-nd[i+1])*(nd[i]-nd[i+1])+(ndy[i]-ndy[i+1])*(ndy[i]-ndy[i+1]))); } main(){ n=read(),k=read(); for(int i=1;i<=n;i++)nd[i*2-2]=read(),ndy[i*2-2]=read(),nd[i*2-1]=read(),ndy[i*2-1]=read(); for(int i=0;i<n+n;i++) rk[i]=i; sort(rk,rk+n*2,cmp); int now=1;pos[rk[0]]=1; for(int i=1;i<n+n;i++){ if(nd[rk[i]]!=nd[rk[i-1]]) now++; pos[rk[i]]=now; } // for(int i=0;i<n+n;i++) printf("%d ",pos[i]);puts(""); ins(S,1,k,0); for(int i=1;i<now*2;i++) ins(i,i+1,k,0); ins(now*2,T,k,0); for(int i=0;i<n+n;i+=2){ if(pos[i]==pos[i+1])ins(pos[i]*2-1,pos[i+1]*2,1,len(i)); else ins(pos[i]*2,pos[i+1]*2-1,1,len(i)); } solve(); printf("%lld\n",mincost); }
23.火星探险问题
和深海机器人问题差不多的。最大费用最大流。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define inf 0x3f3f3f3f #define S 0 #define T 2455 #define MN 40 #define ME 12000 int maxflow,mincost; struct edge{int to,w,c,nex;}e[ME+5]; int d[T+5],q[ME*2],hr[T+5],cnt=1,l,r; bool vis[T+5],inq[T+5]; inline void ins(int f,int t,int w,int c){ e[++cnt]=(edge){t,w,c,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,-c,hr[t]};hr[t]=cnt; } inline bool spfa(){ memset(d,128,sizeof d); q[l=r=ME]=T;inq[T]=1;d[T]=0; while(l<=r){ int u=q[l++];inq[u]=0; for(int i=hr[u];i;i=e[i].nex) if(e[i^1].w&&d[e[i].to]<d[u]-e[i].c){ d[e[i].to]=d[u]-e[i].c; if(!inq[e[i].to]) d[e[i].to]>d[q[l]]?q[--l]=e[i].to:q[++r]=e[i].to,inq[e[i].to]=1; } } return d[S]>0; } inline int mcf(int x,int f){ vis[x]=1; if(x==T) return f; int used=0,w; for(int i=hr[x];i;i=e[i].nex) if(!vis[e[i].to]&&d[e[i].to]==d[x]-e[i].c&&e[i].w){ w=mcf(e[i].to,min(f-used,e[i].w)); used+=w;e[i].w-=w;e[i^1].w+=w; mincost+=e[i].c*w; if(f==used) return used; } return d[x]=-1,used; } inline void solve(){ while(spfa()){ do{ memset(vis,0,sizeof vis); maxflow+=mcf(S,inf); }while(vis[T]); } } int n,m,k,tot; int mp[MN][MN],pos[MN][MN],step[MN][MN]; inline void dfs(int id,int x,int y){ if(x==n&&y==m) return; if(step[x+1][y]&&x+1<=n&&y<=m){ // printf("%d %d\n",x+1,y); printf("%d 0\n",id); step[x+1][y]--; dfs(id,x+1,y); } else if(step[x][y+1]&&x<=n&&y+1<=m){ // printf("%d %d\n",x,y+1); printf("%d 1\n",id); step[x][y+1]--; dfs(id,x,y+1); } } int main(){ k=read(),m=read(),n=read(); register int i,j; for(i=1;i<=n;i++) for(j=1;j<=m;j++){ pos[i][j]=(i-1)*m+j; mp[i][j]=read(); if(mp[i][j]==1) mp[i][j]=-1; if(mp[i][j]==2) mp[i][j]=++tot; } for(i=1;i<=n;i++)for(j=1;j<=m;j++)if(mp[i][j]>=0){ if(i<n&&mp[i+1][j]>=0) ins(pos[i][j],pos[i+1][j],inf,0); if(j<m&&mp[i][j+1]>=0) ins(pos[i][j],pos[i][j+1],inf,0); if(mp[i][j]>0){ ins(pos[i][j],n*m+mp[i][j],1,1); if(i<n&&mp[i+1][j]>=0) ins(n*m+mp[i][j],pos[i+1][j],inf,0); if(j<m&&mp[i][j+1]>=0) ins(n*m+mp[i][j],pos[i][j+1],inf,0); } } ins(S,1,k,0);ins(n*m,T,inf,0);if(mp[n][m]>0) ins(mp[n][m]+n*m,T,inf,0); solve(); for(i=1;i<=n;i++)for(j=1;j<=m;j++)for(int p=hr[pos[i][j]];p;p=e[p].nex)if(p&1) step[i][j]+=e[p].w; for(i=1;i<=maxflow;i++){ dfs(i,1,1); } return 0; }
24.骑士共存问题
最小割。首先将图进行黑白染色,然后将会相互攻击到的点之间连一条inf的边,S向黑点连流量为1的边,白点向T连流量为1的边。跑最大流。

#include<bits/stdc++.h> using namespace std; inline int read(){ int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} return x*f; } #define MN 205 #define T 40005 #define S 0 #define ME 500000 #define inf 200000000 #define p pd(i,j,x,y) int cnt=1,d[T+5],hr[T+5],cur[T+5],q[T+5],top,ans; struct edge{int to,w,nex;}e[ME]; inline void ins(int f,int t,int w){ e[++cnt]=(edge){t,w,hr[f]};hr[f]=cnt; e[++cnt]=(edge){f,0,hr[t]};hr[t]=cnt; } inline bool bfs(){ memset(d,0,sizeof d); register int i,j; for(d[q[i=top=1]=S]=1;i<=top;i++) for(j=hr[q[i]];j;j=e[j].nex) if(e[j].w&&!d[e[j].to]) d[q[++top]=e[j].to]=d[q[i]]+1; return d[T]; } inline int dfs(int x,int f){ if(x==T) return f;int used=0; for(int i=cur[x];i;i=e[i].nex){ cur[x]=i; if(e[i].w&&d[e[i].to]==d[x]+1){ int w=dfs(e[i].to,min(f-used,e[i].w)); e[i].w-=w,used+=w,e[i^1].w+=w; if(used==f) return used; } } return d[x]=-1,used; } inline void dinic(){ while(bfs()){ memcpy(cur,hr,sizeof(int)*(T+5)); ans+=dfs(S,inf); } } int n,m; bool mp[MN][MN]; int g(int x,int y){return (x-1)*n+y;} void pd(int i,int j,int x,int y){ if(x>0&&x<=n&&y>0&&y<=n&&!mp[x][y]) ins(g(i,j),g(x,y),inf); } int main(){ n=read(),m=read(); register int i,j,x,y; for(i=1;i<=m;i++) x=read(),mp[x][read()]=1; for(i=1;i<=n;i++)for(j=1;j<=n;j++)if(!mp[i][j]) (i^j)&1?ins(S,g(i,j),1):ins(g(i,j),T,1); for(i=1;i<=n;i++)for(j=1;j<=n;j++)if(!mp[i][j]&&(i^j)&1){ x=i-2;y=j+1;p; x=i-2;y=j-1;p; x=i-1;y=j+2;p; x=i-1;y=j-2;p; x=i+2;y=j+1;p; x=i+2;y=j-1;p; x=i+1;y=j+2;p; x=i+1;y=j-2;p; } dinic(); printf("%d\n",n*n-m-ans); return 0; }
来自PaperCloud的博客,未经允许,请勿转载,TKS。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号