Chapter 9 多重网格法

【定义9.1】方程组 \(\boxed{A\mathbf{x} = \mathbf{b}}\) 的近似解 \(\tilde{\mathbf{x}}\) 的误差为 \(\mathbf{e}(\tilde{\mathbf{x}}) := \mathbf{x}-\tilde{\mathbf{x}}\)，残差为 \(\mathbf{r}(\mathbf{\tilde{x}}):= \mathbf{b} - A\mathbf{\tilde{x}}\)。

【推论9.2】残差和误差满足关系：\(A\mathbf{e} = \mathbf{r}\)。

【定义9.3】 矩阵的条件数为 \(\mathrm{cond}(A) := \|A\|_2\|A^{-1}\|_2\)。

【定理9.4】近似解的相对误差被其相对残差控制：

\[\dfrac{1}{\text{cond}(A)}\dfrac{\|\mathbf{r}\|_2}{\|\mathbf{b}\|_2} \le \dfrac{\|\mathbf{e}\|_2}{\|\mathbf{x}\|_2} \le \textrm{cond}(A)\dfrac{\|\mathbf{r}\|_2}{\|\mathbf{b}\|_2} \]

证明：

根据矩阵范数的定义，\(\|A\|_2\|\mathbf{e}\|_2 \geq \|\mathbf{r}\|_2, \|A^{-1}\|_2\|\mathbf{b}\|_2 \geq \|\mathbf{x}\|_2 \Rightarrow \dfrac{1}{\text{cond}(A)}\dfrac{\|\mathbf{r}\|_2}{\|\mathbf{b}\|_2} \le \dfrac{\|\mathbf{e}\|_2}{\|\mathbf{x}\|_2}\)。

另一边类似。

【定义9.6】多重网格法的模型问题是具有齐次边界条件的一维 Poisson 方程：

\[\begin{cases} \begin{aligned} -\Delta u &= f \quad \text{in}\ \Omega := (0, 1); \\ u&=0 \quad \text{on}\ \partial \Omega. \end{aligned} \end{cases} \tag{9.6} \]

【例9.7】对于 【例7.10】 的一个特殊情况 \(\alpha = \beta = 0,m = n - 1\)，\((9.6)\) 离散化后得到的线性系统为 \(\boxed{A\mathbf{u} = \mathbf{f}}\)，我们以 \(h = \frac1n\) 为间隔划分定义域，其中 \(x_j = jh = \frac {j}n\)，未知量为 \(u_j(j = 1, 2, \cdots, n-1)\)。

矩阵 \(A=(a_{ij})_{n\times n}\)，\(a_{ij} = \begin{cases}\frac2{h^2} & \text{if}\ i = j; \\ -\frac1{h^2} & \text{if}\ i-j=\pm 1; \\ 0 & \text{otherwise.}\end{cases}\)。根据 【引理7.25】特征值与特征向量为：

\[\lambda_k(A) = \frac4{h^2} \sin^2 \frac{k\pi}{2n} = \frac4{h^2}\sin^2 \frac{kh\pi}2, \\ w_{k,j} = \sin \frac{jk\pi}n = \sin(x_j k \pi) \\ j,k = 1, 2, \cdots, n-1 \]

9.3 Algorithmic componets

9.3.1 Fourier modes on \(\Omega^h\)

【定义9.9】正弦波的波数 \(k = \dfrac{2}{L}\)，其中 \(L\) 为波长。

【引理9.10】波数为 \(k\) 的 Fourier mode （其在的第 \(j\) 个位置值为 \(w_{k,j} = \sin(x_j k \pi)\) ）波长为 \(L = \frac2k\)。

证明： 根据定义9.9，\(\sin(x_j k\pi) = -\sin (x_j + \frac{L}2)k\pi\)，所以 \(x_j k \pi = (x_j + \frac{L}2)k\pi - \pi\)。所以 \(k = \frac2L\)。

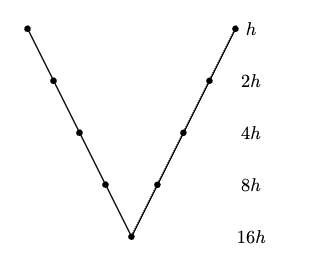
【练习9.11】对于 \(\Omega = (0, 1)\)，\(\Omega^h\) 所能表示的最大波数为 \(n_{max} = \frac1h\)。（类似用离散点来拟合正弦函数）。

【引理9.12】（Aliaising）对于 \(\Omega^h\) ，\(k\in (n, 2n)\)，Fourier mode \(\mathbf{w}_k\) （其在的第 \(j\) 个位置值为 \(w_{k,j} = \sin(x_j k \pi)\) ）实际上表示为 \(\mathbf{w}_{k'}\)，其中 \(k'= 2n - k\)。

证明： \(\sin (x_j k \pi) = -\sin(2j\pi - x_j k \pi) = -\sin (x_j(2n - k)\pi) = -\sin (x_j k'\pi) = -w_{k',j}\)

【定义9.15】对于 \(\Omega^h\)，称波数 \(k\in [1, \frac{n}2)\) 为低频（LF）或 smooth modes，\(k\in [\frac{n}2,n]\) 为高频（HF）或 oscillatory modes。

9.3.2 Relaxation

【定义8.2】对于 \(\boxed{A\mathbf{x} = \mathbf{b}}\)，Jacobi 迭代的形式为：\(a_{ii}x_i^{(k+1)} = - \sum\limits_{j\neq i;j=1}^n a_{ij}x_j^{(k)} + b_i\)。

定义 \(D,-L,-U\) 为 \(A\) 的对角，下三角，上三角部分（\(A = D - L - U\)）。定义：

\[\begin{cases} T_J = D^{-1}(L + U), \\ \mathbf{c} = D^{-1}\mathbf{b}. \end{cases} \]

【定义8.9】带权 Jacobi 迭代为如下形式的不动点迭代：

\[\mathbf{x}_* = T_J \mathbf{x}^{(k)}+ \mathbf{c} \\ \mathbf{x}^{k+1} = (1 - \omega)\mathbf{x}^{(k)} + \omega \mathbf{x}_* = [(1-\omega)I + \omega T_J]\mathbf{x}^{(k)} + \mathbf{c} \]

【引理9.16】对于 \(\boxed{A\mathbf{x} = \mathbf{b}}\)，带权 Jacobi 迭代矩阵为 \(T_{\omega} = (1 - \omega)I+\omega D^{-1}(L+U) = I - \dfrac{\omega h^2}{2}A\)，其特征向量与 \(A\) 一样，对应的特征值 \(\lambda_k (T_{\omega}) = 1- 2\omega \sin^2 \dfrac{k\pi}{2n}\)。

【定义9.19】迭代方法的平滑因子 \(\mu\) 是 HF modes 下最大阻尼因子：

\[\mu := \min_{\omega \in (0, 1]} \max_{k\in [\frac{n}2, n)} | \lambda_k (T_{\omega})|, \]

如果 \(\mu\) 很小并且与网格大小无关，则迭代方法具有平滑特性。

【例9.20】对于 \(\lambda_k (T_{\omega}) = 1- 2\omega \sin^2 \dfrac{k\pi}{2n}\)，固定 \(\omega\) 后 \(\lambda_k(T_{\omega})\) 关于 \(k\) 单调递减，所以应当满足 \(\lambda_{\frac{n}2}(T_{\omega}) = -\lambda_n(T_{\omega}) \Rightarrow \omega = \frac23\)，所以 \(\mu = \frac13\)。

9.3.3 Restriction and prolongation

定义：\(w_{k,j}^{h} = \sin(hjk\pi)\)。\(n = \frac1h\)。

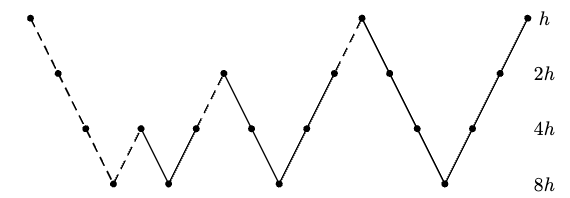
【引理9.22】\(\Omega^h\) 上第 \(k\) 个 LF mode 和 \(\Omega^{2h}\) 上第 \(k\) 个 mode 之间具有关系：\(w_{k,2j}^h = w_{k,j}^{2h}\)。在 \(\Omega^h\) 上的 LF modes \(k\in [\frac{n}4, \frac{n}2)\) 将变为 \(\Omega^{2h}\) 上的 HF modes。

【定义9.23-25】限制算子 \(I_h^{2h}:\mathbb{R}^{n-1} \to \mathbb{R}^{\frac{n}2 - 1}\) 表示从精细网格 \(\Omega^h\) 到粗网格 \(\Omega^{2h}\) 的映射：\(I_h^{2h}\mathbf{v}^h = \mathbf{v}^{2h}\)。

• injection 算子，形式为 \(v_j^{2h} = v_{2j}^h, j = 1, 2, \cdots, \frac{n}2 - 1\)。
• full-weighting 算子，形式为 \(v_j^{2h} = \frac14 (v_{2j-1}^h + 2v_{2j}^h + v_{2j+1}^h),j=1,2,\cdots,\frac{n}2-1\)。

【定义9.27-28】prolongation（延长）或 interpolation 插值算子 \(I_{2h}^h:\mathbb{R}^{\frac{n}2 -1}\to\mathbb{R}^{n-1}\)，将粗网格向精细网格映射：\(I_{2h}^h \mathbf{v}^{2h} = \mathbf{v}^h\)。

• 线性插值算子，形式为 \(v_{2j}^h = v_j^{2h}, v_{2j+1}^h = \frac12(v_j^{2h}+v_{j+1}^{2h})\)。

9.3.4 Two-grid correction

【定义9.30】two-grid correction 用于解决【例9.7】中的 \(\boxed{A\mathbf{u} = f}\) ，形式如下：

\[\mathbf{v}^h \leftarrow \texttt{TG}(\mathbf{v}^h, \mathbf{f}^h, \nu_1, \nu_2) \]

1. 对 \(A^h\mathbf{u}^h = \mathbf{f}^h\) 在 \(\Omega^h\) 松弛 \(\nu_1\) 次，初始设置 \(\mathbf{v}^h\)  ，\(\mathbf{v}^h \leftarrow T_{\omega}^{\nu_1}\mathbf{v}^h + \mathbf{c}_1(f)\)。
2. 计算精细网格残差 \(\mathbf{r}^h = \mathbf{f}^h - A^h\mathbf{v}^h\)，将其限制在粗网格上（\(\mathbf{r}^{2h} = I_h^{2h}\mathbf{r}^h\)）：\(\mathbf{r}^{2h}\leftarrow I_h^{2h}(\mathbf{f}^{h} - A^h\mathbf{v}^h)\)。
3. 在 \(\Omega^{2h}\) 是上求解 \(A^{2h}\mathbf{e}^{2h} = \mathbf{r}^{2h}\)：\(\mathbf{e}^{2h} \leftarrow (A^{2h})^{-1}\mathbf{r}^{2h}\)。
4. 在粗网格上插值（\(\mathbf{e}^{h} = I_{2h}^h \mathbf{e}^{2h}\)）并校正精细网格上的估计：\(\mathbf{v}^h \leftarrow \mathbf{v}^h + I_{2h}^h\mathbf{e}^{2h}\)。
5. 对 \(A^h\mathbf{u}^h = \mathbf{f}^h\) 在 \(\Omega^h\) 松弛 \(\nu_2\) 次，初始设置 \(\mathbf{v}^h\)  ，\(\mathbf{v}^h \leftarrow T_{\omega}^{\nu_2}\mathbf{v}^h + \mathbf{c}_2(f)\)。

【引理9.31】two-grid correction 的误差向量的迭代矩阵是 \(TG = T_{\omega}^{\nu_2}[I - I_{2h}^h (A^{2h})^{-1}I_h^{2h}A^h]T_{\omega}^{\nu_1}\)。

证明：

\[\mathbf{v}^h \leftarrow T_{\omega}^{\nu_2}(T_{\omega}^{\nu_1}\mathbf{v}^h+\mathbf{c}_1(f)+I_{2h}^h(A^{2h})^{-1}I_{h}^{2h}(f^h - A^h(T_{\omega}^{\nu_1}\mathbf{v}^h + \mathbf{c}_1(f)))) + \mathbf{c}_2(f) \]

因为是不动点迭代，所以上式中 \(\mathbf{v}^h\) 若取 \(\mathbf{u}^h\) 则左右相等，所以左右都减去 \(\mathbf{u}^h\) 可以得到

\[\mathbf{e}^h \leftarrow T_{\omega}^{\nu_2}[I - I_{2h}^h (A^{2h})^{-1}I_h^{2h}A^h]T_{\omega}^{\nu_1} \mathbf{e}^h \]

9.3.5 Multigrid cycles

【定义9.32】V-cycles 用于解决【例9.7】中的 \(\boxed{A\mathbf{u} = f}\) ，形式如下：

\[\mathbf{v}^h \leftarrow \texttt{VC}(\mathbf{v}^h, \mathbf{f}^h, \nu_1, \nu_2) \]

1. 对 \(A^h\mathbf{u}^h = \mathbf{f}^h\) 在 \(\Omega^h\) 松弛 \(\nu_1\) 次，初始设置：\(\mathbf{v}^h\)。
2. 如果 \(\Omega^h\) 是粗网格，转4，否则：

\[\begin{aligned} \mathbf{f}^{2h} &\leftarrow I_h^{2h}(\mathbf{f}^h - A^h \mathbf{v}^h), \\ \mathbf{v}^{2h} &\leftarrow \mathbf{0}, \\ \mathbf{v}^{2h} &\leftarrow \texttt{VC}^{2h}(\mathbf{v}^{2h}, \mathbf{f}^{2h}, \nu_1, \nu_2). \end{aligned} \]

3. 校正：\(\mathbf{v}^h \leftarrow \mathbf{v}^h + I_{2h}^h\mathbf{v}^{2h}\)。
4. 对 \(A^h\mathbf{u}^h = \mathbf{f}^h\) 在 \(\Omega^h\) 松弛 \(\nu_2\) 次，初始设置：\(\mathbf{v}^h\)。

【引理9.33】D维区间，每维 \(n=2^m\) 个网格，V-cycles 需要内存为

\[2n^D(1 + 2^{-D}+2^{-2D}+\cdots+2^{-mD}) < \dfrac{2n^D}{1-2^{-D}}. \]

设 WU 为一次精细网格上 relacation sweep 的计算成本，在忽略网格内转移后，单个V循环的计算成本（\(\nu_1 = \nu_2 = 1\)）为

\[2\text{WU}(1+2^{-D}+\cdots+2^{-mD}) < \dfrac{2}{1-2^{-D}}\text{WU}. \]

【定义9.34】full multigrid V-cycle 用于解决【例9.7】中的 \(\boxed{A\mathbf{u} = f}\) ，形式如下：

\[\mathbf{v}^h \leftarrow \texttt{FMG}^h(\mathbf{f}^h, \nu_1, \nu_2) \]

1. 若 \(\Omega^h\) 是粗网格，设置 \(\mathbf{v}^h \leftarrow \mathbf{0}\)，转3，否则

\[\begin{aligned} \mathbf{f}^{2h} &\leftarrow I_h^{2h}\mathbf{f}^{2h}, \\ \mathbf{v}^{2h} &\leftarrow \texttt{FMG}^{2h}(\mathbf{f}^{2h}, \nu_1, \nu_2). \end{aligned} \]

2. 校正：\(\mathbf{v}^h \leftarrow \mathbf{v}^h + I_{2h}^h\mathbf{v}^{2h}\)。
3. 执行一个 V 循环使用初始值 \(\mathbf{v}^h\)：\(\mathbf{v}^h \leftarrow \texttt{VC}^h(\mathbf{v}^h, \mathbf{f}^h, \nu_1, \nu_2)\)。

9.4 收敛性分析

9.4.1 谱分析

【定义9.36】称 Fourier mode \(\mathbf{w}_k^h, k\in [1, \frac{n}2)\) 和 \(\mathbf{w}_{k'}^h, k' = n - k\) 是 \(\Omega^h\) 上互补的(complemetnary modes)。

【引理9.37】一对互补的 Fourier modes 满足

\[w_{k',j}^h = (-1)^{j+1} w_{k,j}^h. \]

证明：\(w_{k',j}^h = \sin \dfrac{(n-k)j\pi}{n} = \sin(j\pi - \dfrac{kj\pi}n) = (-1)^{j+1}w_{k,j}^h\)。

【引理9.38】作用在 \(\Omega^h\) 上互补的 Fourier modes 上的 full-weighting 算子为：

\[I_h^{2h} \mathbf{w}_k^h = c_k \mathbf{w}_k^{2h} := \cos^2 \dfrac{k\pi}{2n}\mathbf{w}_k^{2h}, \\ I_h^{2h} \mathbf{w}_{k'}^h = -s_k \mathbf{w}_k^{2h} := -\sin^2 \dfrac{k\pi}{2n}\mathbf{w}_k^{2h}, \]

\(k\in [1, \frac{n}2), k' = n - k\)，特别的 \(I_h^{2h}\mathbf{w}_{\frac{n}2}^h = \mathbf{0}\)。

证明：对于低频mode \(k\)，有

\[\begin{aligned} &(I_h^{2h}\mathbf{w}_k^h)_j \\ =&\frac14 \sin \frac{(2j-1)k\pi}{n} + \frac12 \sin \frac{2jk\pi}{n} + \frac14 \sin \frac{(2j+1)\pi}{n} \\ =& \frac12 (1 + \cos \frac{k\pi}n)\sin \frac{2jk\pi}n = \cos^2 \frac{k\pi}{2n} w_{k,j}^{2h} \end{aligned} \]

【引理9.39】作用在 \(\Omega^{2h}\) 上的线性插值算子为

\[I_{2h}^h \mathbf{w}_k^{2h} = c_k \mathbf{w}_k^h - s_k \mathbf{w}_{k'}^h, k' = n - k \]

证明：由 Lem 9.37 得，

\[c_k w_{k,j}^h - s_k w_{k',j}^h = \left( \cos^2 \frac{k\pi}{2n} + (-1)^j \sin^2 \frac{k\pi}{2n} \right)w_{k,j}^h = \begin{cases} w_{k,j}^h \quad \text{if j is even} \\ \cos \frac{k\pi}n w_{k,j}^h \quad \text{if j is odd} \end{cases} \]

另一方面，根据 Def 9.28

\[(I_{2h}^h \mathbf{w}_k^{2h})_j = \begin{cases} w_{k,j}^h, & \text{if j is even} \\ \frac12 (\sin \frac{k\pi (j - 1)}n + \sin \frac{k\pi (j + 1)}n) & \text{if j is odd} \end{cases} \]

备注：\(w_{k,j}^h = \sin jkh\pi\)，$\frac12 (w_{k,\frac{j}2-\frac12}^{2h} + w_{k,\frac{j}2+\frac12}^{2h}) =\frac12 (\sin kh\pi (j - 1) + \sin k\pi (j + 1)h) $​。

【定理9.40】双网格校正在子空间 \(W_k^h = \text{span} \{\mathbf{w}_k^h, \mathbf{w}_{k'}^h\}\) 上不变，

\[TG_{\mathbf{w}_k} = \lambda_k^{\nu_1 + \nu_2}s_k \mathbf{w}_k + \lambda_k^{\nu_1}\lambda_{k'}^{\nu_2} s_k \mathbf{w}_{k'} \\ TG_{\mathbf{w}_{k'}} = \lambda_{k'}^{\nu_1} \lambda_k^{\nu_2} c_k \mathbf{w}_k + \lambda_{k'}^{\nu_1 + \nu_2}c_k \mathbf{w}_{k'} \]

其中 \(\lambda_k\) 是 \(T_{\omega}\) 的特征值。

证明：注意到 \(A^h\) 的特征值是 \(\frac4{h^2}s_k\) 考虑 \(\nu_1 = \nu_2 = 0\) 的情形，

\[\begin{aligned} &A^h\mathbf{w}_k^h = \frac{4s_k}{h^2} \mathbf{w}^h_k \\ \Rightarrow & I_h^{2h} A^h \mathbf{w}_k^h = \frac{4c_k s_k}{h^2} \mathbf{w}_k^{2h} \\ \Rightarrow & (A^{2h})^{-1} I_h^{2h} A^h \mathbf{w}_k^h = \frac{4c_k s_k}{h^2} \frac{(2h)^2}{4\sin^2 \frac{k\pi}n}\mathbf{w}_k^{2h} = \mathbf{w}_k^{2h} \\ \Rightarrow & - I_{2h}^h (A^{2h})^{-1} I_h^{2h} A^h \mathbf{w}_k^{h} = -c_k \mathbf{w}_k^h + s_k \mathbf{w}_{k'}^h \\ \Rightarrow &[I - I_{2h}^h (A^{2h})^{-1} I_h^{2h} A^h] \mathbf{w}_k^h = s_k \mathbf{w}_k^h + s_k\mathbf{w}_{k'}^h ~~~~~~~~~~~~~~\text{(1)} \end{aligned} \]

相似的，

\[\begin{aligned} &A^h\mathbf{w}_{k'}^h = \frac{4s_{k'}}{h^2} \mathbf{w}^h_{k'} = \frac{4c_k}{h^2}\mathbf{w}_{k'}^h \\ \Rightarrow & I_h^{2h} A^h \mathbf{w}_{k'}^h = -\frac{4c_k s_k}{h^2} \mathbf{w}_k^{2h} \\ \Rightarrow & (A^{2h})^{-1} I_h^{2h} A^h \mathbf{w}_{k'}^h = -\frac{4c_k s_k}{h^2} \frac{(2h)^2}{4\sin^2 \frac{k\pi}n}\mathbf{w}_k^{2h} = -\mathbf{w}_k^{2h} \\ \Rightarrow & - I_{2h}^h (A^{2h})^{-1} I_h^{2h} A^h \mathbf{w}_{k'}^{h} = c_k \mathbf{w}_k^h - s_k \mathbf{w}_{k'}^h \\ \Rightarrow &[I - I_{2h}^h (A^{2h})^{-1} I_h^{2h} A^h] \mathbf{w}_{k'}^h = c_k \mathbf{w}_k^h + c_k\mathbf{w}_{k'}^h~~~~~~~~~~~~~~\text{(2)} \end{aligned} \]

加入前松弛后后松弛，前松弛对 (1) 乘 \(\lambda_k^{\nu_1}\)，对 (2) 乘 \(\lambda_{k'}^{\nu_1}\)，后松弛对 \(\mathbf{w}_k^h\) 乘 \(\lambda_{k}^{\nu_1}\)，对 \(\mathbf{w}_{k'}^{\nu_2}\) 乘 \(\lambda_k^{\nu_2}\)。最后得到定理中的两个式子。

9.4.2 代数图像

【引理9.42】全加权算子和线性插值算子满足：\(I_{2h}^h = c(I_h^{2h})^T, I_h^{2h}A^hI_{2h}^h = A^{2h},c =2\)。

【引理9.43】线性插值矩阵的一组基是它的全体列向量，因此 \(\dim \mathcal{R}(I_{2h}^h) = \frac{n}2 - 1, \mathcal{N}(I_{2h}^h) = \{\mathbf{0}\}\)。

证明：记 \(\mathbf{v}^{2h} = \sum v_j^{2h}\mathbf{e}_j^{2h}\)，则 \(I_{2h}^h \mathbf{v}^{2h} = \sum v_j^{2h} I_{2h}^h \mathbf{e}_j^{2h}\)，其中 \(I_{2h}^h \mathbf{e}_j^{2h}\) 是 \(I_{2h}^h\) 的列。（\(I_{2h}^h\) 是满秩的） 。

【引理9.44】full-weighting 算子满足：\(\dim \mathcal{R}(I_h^{2h}) = \frac{n}2 - 1, \quad \dim \mathcal{N}(I_{h}^{2h}) = \frac{n}2\)。

【引理9.46】full-weighting 算子的核空间 \(\mathcal{N}(I_h^{2h}) = \text{span}\{A^h\mathbf{e}_j^h: j ~~\text{is odd}\}\)​​。

证明：

\[(I_h^{2h})_j = [0, \cdots, 0, \frac14, \frac12, \frac14, 0, \cdots, 0]^T,\quad\text{非0项是}2j-1，2j,2j+1 项 \]

考虑矩阵 \(I_h^{2h}A^h\)，即 \(\sum_{i = 1}^{n-1}(I_h^{2h})_{ji}(A^h)_{ik} = \begin{cases}-\frac14& k = 2j\pm2 \\0& k = 2j\pm1\\\frac12&k = 2j\end{cases}\)。

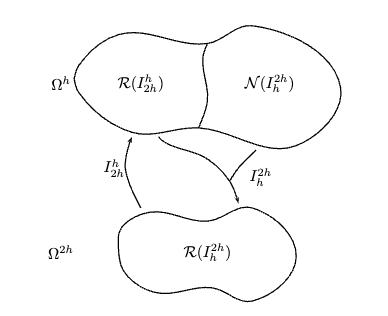
【引理9.47】不带松弛的二网格校正的核空间是线性插值的像空间：\(\mathcal{N}(TG) = \mathcal{R}(I_{2h}^h)\)。

证明：设 \(\mathbf{s}^h \in \mathcal{R}(I_{2h}^h), \exists \mathbf{q}^{2h} \in \mathbb{R}^{\frac{n}2 - 1}, \mathbf{s}^h = I_{2h}^h \mathbf{q}^{2h}\)​。

\[TG \mathbf{s}^h = [I - I_{2h}^h (A^{2h})^{-1}I_h^{2h}A^h]I_{2h}^h\mathbf{q}^{2h} = = [I_{2h}^h - I_{2h}^h(A^{2h})^{-1}A^{2h}]\mathbf{q}^{2h} = \mathbf{0}\cdot \mathbf{q}^{2h} = \mathbf{0} \]

所以 \(\mathcal{R}(I_{2h}^h) \subseteq \mathcal{N}(TG)\)。

设 \(\mathbf{t}^h \in \mathcal{N}(I_h^{2h}A^h)\)，

\[TG\mathbf{t}^h = [I - I_{2h}^h (A^{2h})^{-1}I_h^{2h}A^h]\mathbf{t}^h = \mathbf{t}^h \]

根据线性映射基本定理，\(n - 1 = \dim \mathcal{N}(TG) + \dim \mathcal{R}(TG)\)。因为 TG 是 \(\mathcal{N}(I_h^{2h}A^h)\) 上的恒等映射，所以

\[\dim \mathcal{R}(TG) \ge \dim \mathcal{N}(I_h^{2h}A^h) = \dim \mathcal{N}(I_h^{2h}) = \frac{n}2 \]

所以 \(\dim \mathcal{N}(TG) \le \frac{n}2 - 1 = \dim \mathcal{R}(I_{2h}^h)\)，所以得证。

【定义9.48】设 \(A\)  为 \(n\) 阶正定矩阵，记 \(A-\)内积为 \(\langle \mathbf{u}, \mathbf{v}\rangle_A := \langle A\mathbf{u}, \mathbf{v}\rangle = \mathbf{u}^T A \mathbf{v}\)，\(A-\)范数为 \(\| \mathbf{u}\|_A:= \sqrt{\langle \mathbf{u}, \mathbf{u}\rangle_A}\)；若 \(\langle \mathbf{u}, \mathbf{v}\rangle_A = 0\)，则称 \(\mathbf{u,v}\) 是 \(A-\)​正交。

9.4.3 FMG 的最优复杂性

【定义9.49】FMG 的误差为 \(E_i^h:= v_i^h - u(x_i)=v_i^h - u_i^h + u_i^h - u(x_i)\)。其中 \(v_i^h - u_i^h\) 是线性方程组的求解误差，而 \(u_i^h - u(x_i)\) 是截断误差。

【引理9.50】从粗网格到细网格进行线性插值，有

\[\sqrt{c} \| \mathbf{v}^{2h} - \mathbf{u}^{2h} \|_{A^{2h}} = \| I_{2h}^h \mathbf{v}^{2h} - I_{2h}^h \mathbf{u}^{2h} \|_{A^h}, c = 2 \]

证明：

\[\begin{aligned} &\| \mathbf{v}^{2h} - \mathbf{u}^{2h}\|_{A^{2h}}^2\\ =&\langle A^{2h}(\mathbf{v}^{2h} - \mathbf{u}^{2h}), \mathbf{v}^{2h} - \mathbf{u}^{2h} \rangle\\ =&\langle I_h^{2h}A^h I_{2h}^h (\mathbf{v}^{2h} - \mathbf{u}^{2h}), \mathbf{v}^{2h} - \mathbf{u}^{2h}\rangle\\ =&\left\langle A^h I_{2h}^h(\mathbf{v}^{2h} - \mathbf{u}^{2h}), \frac1c I_{2h}^h (\mathbf{v}^{2h} - \mathbf{u}^{2h})\right\rangle\\ =&\frac1c \| I_{2h}^h\mathbf{v}^{2h} - I_{2h}^h \mathbf{u}^{2h} \|^2_{A^h} \end{aligned} \]

【引理9.51】假设存在一个和网格大小 \(h\) 无关的常数 \(K\in\mathbb{R}^+\) 满足 \(\|I_{2h}^h\mathbf{u}^{2h} - \mathbf{u}^h\|_{A^h} \le Kh^p\)，其中 \(p=2\) 是收敛率。

证明：

数学归纳法。在最粗网格上 FMG 是精确的，多亿归纳基础成立。假设 \(\| \mathbf{e}^{2h}\|_{A^{2h}}\le K(2h)^p\)，在 \(\Omega^h\) 上，

\[\mathbf{e}_0^h = I_{2h}^h \mathbf{v}^{2h} - \mathbf{u}^h \]

在 \(\Omega^h\) 上， \(\mathbf{e}_0^h = I_{2h}^h \mathbf{v}^{2h} - \mathbf{u}^h\)，所以

\[\begin{aligned} \| \mathbf{e}_0^h \|_{A^h} &\le \| I_{2h}^h \mathbf{v}^{2h} - I_{2h}^h \mathbf{u}^{2h}\|_{A^h} + \| I_{2h}^h \mathbf{u}^{2h} - \mathbf{u}^h \|_{A^h} \\ &= \sqrt{c} \| \mathbf{v}^{2h} - \mathbf{u}^{2h} \|_{A^{2h}} + \| I_{2h}^h \mathbf{u}^{2h} - \mathbf{u}^h \|_{A^h} \\ &\le \sqrt{c} K (2h)^p + K h^p = (1 + \sqrt{c}2^p) Kh^p\\ &< 7 K h^p \end{aligned} \]

【定理9.52】一个 FMG 循环复杂度 \(O(\frac1h)\) 可以达到2阶收敛率。

证明： \(\|\mathbf{E}^h\| \le \| \mathbf{u}^h - \mathbf{u}\| + \|\mathbf{u}^h - \mathbf{v}^h \|\)。