「十二省联考 2019」希望
「十二省联考 2019」希望
传送门
Solution
毒瘤题令人。。。。
首先,如果直接计算每个点的贡献就会算重,考虑容斥
发现一个合法方案的合法点集是个联通子图,满足\(V(S)-E(S)=1\)
所以可以把点的贡献和减去边的贡献和
设\(f(x)\)表示以\(x\)为中心的深度不超过\(L\)的联通块数量,\(g(<x,y>)\)表示以\(x,y\)为中心深度均不超过\(L\)的联通块数量
那么答案就是
\[ans=\sum_{i\in V}f(i)^k-\sum_{i\in E}g(i)^k \]根据如下定义
\[f(i)=(dp_{i,L}+1)up_{i,L} \\ g(<x,fa_x>)=(dp_{x,L-1}+1)up_{fa_x,L-1} \]
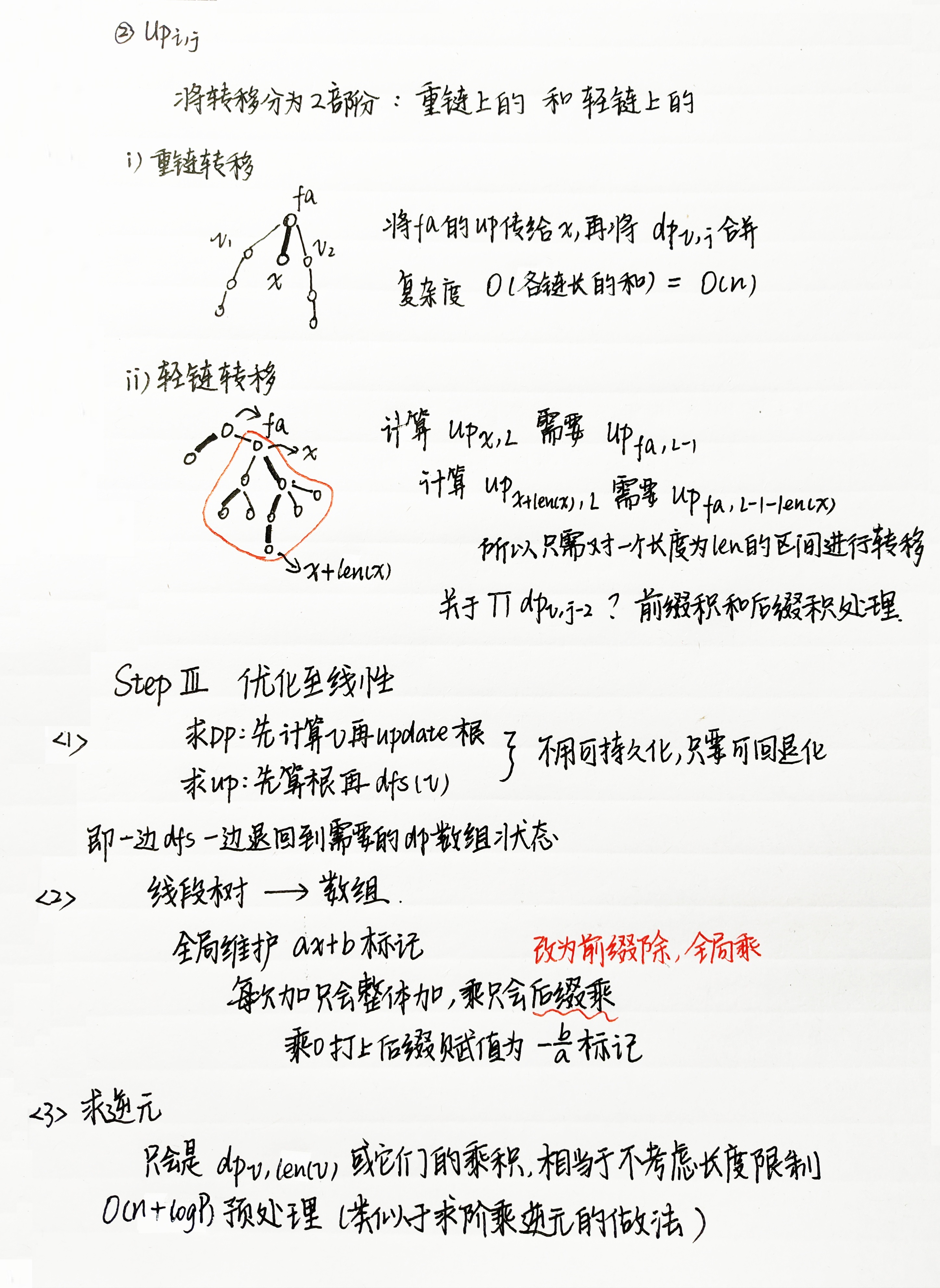
\(update:\)
- 所需要的可回退化数据结构需要维护两个部分
- 每个点以下的重链的全局标记以及后缀打上的赋值标记
- 每个点以下的重链上的单点修改标记,需要开一个stack/vector/list什么的
有一个细节,让我调到了凌晨\(2:30\),就是预处理逆元的时候,要忽视那些\(0\)的。。。。
Code
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define dbg1(x) cerr<<#x<<"="<<(x)<<" "
#define dbg2(x) cerr<<#x<<"="<<(x)<<"\n"
#define dbg3(x) cerr<<#x<<"\n"
using namespace std;
#define reg register
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
const int P=998244353,N=1e6+5;
#define Mul(x,y) (1ll*(x)*(y)%P)
#define Add(x,y) ((x+y)%P)
int fp(int x,int y){int r=1;for(;y;y>>=1,x=Mul(x,x))if(y&1)r=Mul(r,x);return r;}
int n,L,K,ans,a[N][2];
struct ed{int to,nex;}e[N<<1];int en,hr[N];
inline void ins(int x,int y)
{
e[++en]=(ed){y,hr[x]};hr[x]=en;
e[++en]=(ed){x,hr[y]};hr[y]=en;
}
int inv[N],fa[N],len[N*3],son[N],f[N],fac[N],Prod;
void dfs1(int x,int F)
{
len[x]=1;fa[x]=F;f[x]=1;
for(int i=hr[x];i;i=e[i].nex)if(e[i].to^F)
{
dfs1(e[i].to,x);f[x]=Mul(f[x],f[e[i].to]);
if(len[x]<len[e[i].to]+1) len[x]=len[e[i].to]+1,son[x]=e[i].to;
}
(++f[x])%=P;if(f[x])Prod=Mul(Prod,f[x]);
}
int id[N],dfn[N],dind;
void dfs2(int x)
{
id[dfn[x]=++dind]=x;if(son[x])dfs2(son[x]);
for(int i=hr[x];i;i=e[i].nex)
if((e[i].to^fa[x])&&(e[i].to^son[x]))
dfs2(e[i].to);
}
void init()
{
reg int i;Prod=1;dfs1(1,0);dfs2(1);
for(inv[n]=fp(Prod,P-2),i=n-1;i;--i)inv[i]=Mul(inv[i+1],max(f[i+1],1));
for(fac[0]=i=1;i<=n;++i) fac[i]=Mul(fac[i-1],max(f[i],1));
for(i=1;i<=n;++i) inv[i]=Mul(inv[i],fac[i-1]);
}
struct node{int a,b,inva,pos,val;};
struct DP{
vector<pair<node,vector<pair<int,int> > > > _[N];
node tag[N*3];int dp[N*3];
int Val(int x,int y){int r=y<tag[x].pos?dp[x+y]:tag[x].val;return Add(Mul(r,tag[x].a),tag[x].b);}
void Cal(int x,int y,int val){dp[x+y]=Mul(val+P-tag[x].b,tag[x].inva);}
void Cb(int x,int y,int Ly)
{
int i,j;
node ori=tag[x];vector<pair<int,int> >r;
for(i=1;i<=Ly;++i)
{
r.pb(mp(i,dp[x+i]));
if(i==tag[x].pos) dp[x+tag[x].pos++]=tag[x].val;
Cal(x,i,Mul(Val(x,i),Val(y,i-1)));
}
if(Ly<L)
{
int v=f[id[y]];
if(v)
{
r.pb(mp(0,dp[x]));for(i=0,j=inv[id[y]];i<=Ly;++i) Cal(x,i,Mul(Val(x,i),j));
tag[x].a=Mul(tag[x].a,v);tag[x].b=Mul(tag[x].b,v);tag[x].inva=Mul(tag[x].inva,j);
}
else tag[x].pos=Ly+1,tag[x].val=P-Mul(tag[x].b,tag[x].inva);
}
if(x<=n)_[x].pb(mp(ori,r));
}
void dfs(int x)
{
if(son[id[x]])dfs(x+1),tag[x]=tag[x+1];
else tag[x]=(node){1,1,1,n,0};Cal(x,0,1);
for(int i=hr[id[x]];i;i=e[i].nex)
if((e[i].to^son[id[x]])&&(e[i].to^fa[id[x]]))
dfs(dfn[e[i].to]),Cb(x,dfn[e[i].to],min(len[e[i].to]-1,L));
a[x][1]=Val(x,min(L,len[id[x]]-1)),a[x][0]=Val(x,min(L-1,len[id[x]]-1));(++tag[x].b)%=P;
}
void One_step(int x)
{
x=dfn[x];tag[x]=_[x].back().fi;
#define xx (_[x].back().se)
for(int i=xx.size()-1;~i;--i)dp[x+xx[i].fi]=xx[i].se;
_[x].pop_back();
#undef xx
}
void solve(){dfs(1);}
}_dp;
struct UP{
node tag[N];int up[N*3],pos[N],pin,tt,p2[N];
int Val(int x,int y){int r=y<tag[x].pos?up[pos[x]+y]:tag[x].val;return Add(Mul(r,tag[x].a),tag[x].b);}
void Cal(int x,int y,int val){up[pos[x]+y]=Mul(val+P-tag[x].b,tag[x].inva);}
void dfs(int x)
{
if(len[x]-L-1>=0) Cal(x,len[x]-L-1,1);
a[dfn[x]][1]=Mul(a[dfn[x]][1],Val(x,len[x]-1));
if(fa[x]) a[dfn[x]][0]=Mul(a[dfn[x]][0],Add(Val(x,len[x]-1),P-1));
if(!son[x])return;vector<int> c;int v,mL=0,i;
for(i=hr[x];i;i=e[i].nex)if((e[i].to^fa[x])&&(e[i].to^son[x]))c.pb(e[i].to),mL=max(mL,len[e[i].to]);mL=min(mL,L);
reverse(c.begin(),c.end());p2[x]=tt;tt+=mL+1;
_dp.tag[p2[x]]=(node){1,1,1,n,0};_dp.Cal(p2[x],0,1);
for(int o=0;o<c.size();++o)
{
v=c[o];_dp.One_step(x);pos[v]=pin;pin+=len[v];
for(i=max(len[v]-L-1,0);i<len[v];++i)
{
if(~(L-len[v]+i)) up[pos[v]+i]=Mul(Val(x,len[son[x]]-len[v]+i),
Mul(_dp.Val(dfn[x],min(len[x]-1,L-len[v]+i)),_dp.Val(p2[x],min(mL,L-len[v]+i))));
else up[pos[v]+i]=Val(x,len[son[x]]-len[v]+i);
}
tag[v]=(node){1,1,1,n,0};_dp.Cb(p2[x],dfn[v],min(len[v]-1,L));dfs(v);
}
v=son[x];pos[v]=pos[x];tag[v]=tag[x];
for(i=max(len[v]-L,0);i<=len[v]+mL-L-1;++i)
{
if(tag[v].pos==i) up[pos[v]+tag[v].pos++]=tag[v].val;
Cal(v,i,Mul(Val(v,i),_dp.Val(p2[x],L-len[v]+i)));
}
if(mL<L)
{
int va=1,in=1;
for(i=0;i<c.size();++i)va=Mul(va,f[c[i]]),in=Mul(in,inv[c[i]]);
if(!va)tag[v].pos=len[v]+mL-L,tag[v].val=P-Mul(tag[v].b,tag[v].inva);
else
{
for(i=max(len[v]-L-1,0);i<=len[v]+mL-L-1;++i)Cal(v,i,Mul(Val(v,i),in));
tag[v].a=Mul(tag[v].a,va);tag[v].b=Mul(tag[v].b,va);tag[v].inva=Mul(tag[v].inva,in);;
}
}
(++tag[v].b)%=P;dfs(v);
}
void solve()
{
pos[1]=1;tt=n+1;pin=1+len[1];tag[1]=(node){1,1,1,n,0};dfs(1);
for(int i=1;i<=n;++i) ans=Add(ans,fp(a[i][1],K));
for(int i=2;i<=n;++i) ans=Add(ans,P-fp(a[i][0],K));
}
}_up;
int main()
{
n=read();L=read();K=read();int i,j;
for(i=1;i<n;++i) j=read(),ins(j,read());
init();_dp.solve();_up.solve();
return 0*printf("%d\n",ans);
}
Blog来自PaperCloud,未经允许,请勿转载,TKS!
致虚极,守静笃,万物并作,吾以观其复



 浙公网安备 33010602011771号
浙公网安备 33010602011771号