[JLOI 2015]骗我呢

传送门

Description

求给\(n*m\)的矩阵填数的方案数

满足：

\[1\leq x_{i,j}\leq m \]

\[x_{i,j}<x_{i,j+1} \]

\[x_{i,j}<x_{i-1,j+1} \]

Solution 

\(f[i][j]\)表示当前第\(i\)行少的数字是\(j\)的方案数

\[f[i][j]=\sum_{k=1}^{j+1}f[i-1][k]=f[i][j-1]+f[i-1][j+1] \]

观察dp的转移方程

发现它和路径计数的过程很类似

通过等价变化，答案即为：

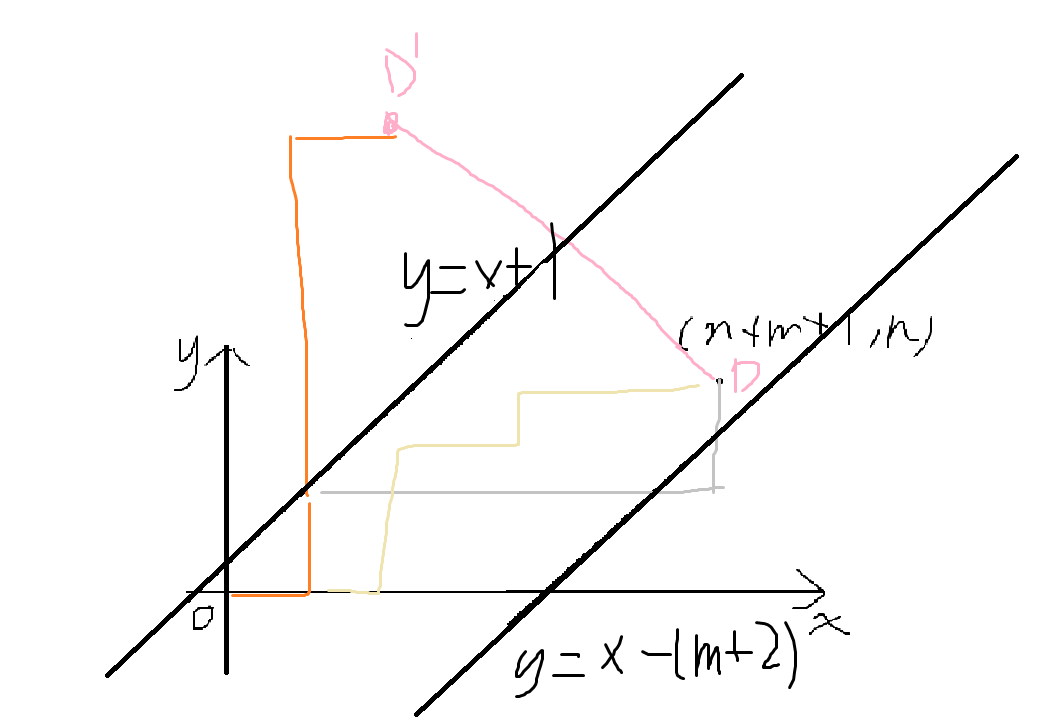
从\((0,0)\)到\((n+m+1,n)\)且不经过直线,\(A:y=x+1\),\(B:y=x-(m+2)\)的方案数

走的方式为只能沿坐标轴的正方向

假如说如果没有限制条件，从\((0,0)\) 到\((x,y)\) 的方案数是\(\binom{x+y}{x}\)

接下来，我们考虑如何进行容斥：

考虑一种关于自身长度奇偶性的容斥

简化一下不合法的经过的路线，有两种情况：\(ABABAB...\)和\(BABABA...\)

这里，如若连着触碰一个条线，我们把它当作是一次

设终点为\((x,y)\)，它关于\(A\)的对称点是\((x_1,y_1)\)

那么从\((0,0)\)到\((x_1,y_1)\)的路径可以对应一条必然经过了一次\(A\)线的路径，所以它的结尾肯定是\(AB\)或\(A\)

将其减去

设\((x_1,y_1)\)关于\(B\)的对称点是\((x2_y2)\)

那么从\((0,0)\)到\((x2,y2)\)的路径可以对应一条必然经过了一次\(BA\)的路径，所以它的结尾肯定是\(BA\)或\(BAB\)

将其加回

......

如此往复，直到不存在所要求的路径的后缀

可以发现，这样一来，恰好所有以\(A\)开头的都被计算了奇数次，也就是被减了一次

以\(B\)开头的不合法路径相似计算即可

Code 

//f[i][j]表示当前第i行少的数字是j的方案数
//f[i][j]=\sum_{k=1}^{j+1}f[i-1][k]=f[i][j-1]+f[i-1][j+1] 
//把改问题转换为路径问题，用组合数加容斥来做 
#include<bits/stdc++.h>
#define reg register
#define ll long long
#define db double
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*f;
}
const int MN=1e6+5,P=1e9+7;
int n,m,M;
int fac[MN<<2],inv[MN<<2];
int Mul(int x,int y){return (1ll*x*y)%P;}
int Add(int x,int y){y=((y%P)+P)%P;return (x+y)%P;}
int X,Y,_,ans;
int C(int x=M,int y=Y)
{
	if(x<0||y<0||y>x)return 0;
	return Mul(Mul(fac[x],inv[y]),inv[x-y]);
}
void _1(){X=Y-1;Y=_+1;_=X;}
void _2(){X=Y+(m+2);Y=_-(m+2);_=X;}
int main()
{
	n=read();m=read();M=2*n+m+1;
	_=X=n+m+1;Y=n;
	fac[0]=fac[1]=inv[0]=inv[1]=1;
	register int i,tmp;
	for(i=2;i<=M;++i) fac[i]=Mul(fac[i-1],i);
	for(i=2;i<=M;++i) inv[i]=Mul(inv[P%i],(P-P/i));
	for(i=2;i<=M;++i) inv[i]=Mul(inv[i-1],inv[i]);
	ans=C();
	for(i=1;;++i)
	{
		if(i&1) _1();else _2();if(X<0||Y<0) break;
		ans=Add(ans,(-1)*(i&1?1:-1)*C());
	}
	_=X=n+m+1;Y=n;
	for(i=1;;++i)
	{
		if(i&1) _2();else _1();if(X<0||Y<0) break;
		ans=Add(ans,(-1)*(i&1?1:-1)*C());
	}
	return 0*printf("%d\n",ans);
}

---

Blog来自PaperCloud，未经允许，请勿转载，TKS！