BA-16 cs231n斯坦佛大学神经网络图像识别课程Refine

 零、鸟瞰卷积神经网络

　  卷积神经网络由多个层次所构成。按照顺序有：输入 - 卷积层 - 激发层 - 缩放层 - 全连接层（放在最后的全连接层被称作分类器层）。

　　英文：INPUT-CONV(convolutional network)-RELU(rectified linear unit)-POOL-FC(fine connected)

　　其中，卷积层用于缩小数据规模的同时负责一部分的学习任务，激发层是纯粹的激发函数阵列，缩放层纯粹用于缩小数据规模，全连接层会承担一部分学习任务。

　　只有卷积层和全连接层具有学习能力。

　　如果去掉卷积层和激发层，缩放层，剩下 {输入 - 全连接层}，那么就得到了一个纯粹线性分类器层，仍然具有一定的学习能力。

　　如果将[卷积层-激发层]打包，[全连接层-缩放层]打包，然后将其堆叠起来 形成如下结构：

　　　　输入 -[卷积层-激发层] x 10-[全连接层-缩放层] x 3- 全连接层分类器

　　就形成了一个比较完整的卷积神经网络，卷积层辅以激发层可以选择缩放或者不缩放，多层堆叠。每一层都可以学习。

　　全连接层辅以缩放层进行缩放，将缩放后且经过数据交给分类器得到最终结果。每一层也都可以学习。

　　以上是卷积神经网络的结构。

　　训练时，每个周期都计算一次惩罚函数，并且利用反向传播算法，逐层调整所有层次中卷积层与全连接层的参数。

　　完成训练，给进去输入，就能拿到输出。准确率一般能达到95%以上（对于小型、低维度、弱逻辑的数据集）。

 一、概述

　　斯坦佛大学的课程包括三个主模块以及一个作业模块。

　　主模块包括：0号模块：环境搭建，该部分指导学生搭建课程所需要的软件环境与数据环境以及作业提交环境。包括python的安装以及相关科学组件numpy等模块。以及用于生成斯坦佛格式的作业文件的命令行程序。但是在自己的原装python环境下，事实上只需要额外命令行执行：

pip install numpy

即可进行课程中所有的实验。原装python环境除了没有来自CIFA-10的大数据集以及没有作业提交系统之外，并没有什么区别。

　　1号模块：神经网络。分为八个小章节。分别介绍了：

　　　　图像识别入门：小学级图像分类技术（kNN）

　　　　线性分类器Classifier：SVM向量机以及Softmax

　　　　优化策略：随机梯度下降法Stochastic Gradiant Descent

　　　　优化的具体方式：反向传播Backpropogation以及对反向传播方法的整体把握

　　　　建立神经网络的第一步：建立整体结构（激活函数、神经网络层次架构以及选择）

　　　　建立神经网络第二步：准备好数据与惩罚函数（数据预处理、参数初始化、泛化规则、惩罚函数）

　　　　建立神经网络第三步：训练与监视（梯度检查、健康评估、训练过程监管、参数更新、超参数优化、模型评估）

　　　　一个迷你的神经网络模型代码实现

　　2号模块：卷积神经网络。分为三个小章节。

　　　　卷积神经网络的结构以及卷积层（卷积层次、层次结构）

　　　　解释卷积神经网络与可视化（相似可视化叠层、反卷积、数据梯度、欺骗、人工比较）

　　　　如何借助面向CV编程技术快速搭建自己的卷积神经网络

二、精炼

　　1号模块：主要介绍神经网络，神经网络包含参数，具有学习能力，在卷积神经网络中，卷积层和全连接层都用到了神经网络。

　　前面几个小单元主要是介绍了为了实现神经网络所需要的技术准备。然后三步走建立完整神经网络。最后一个单元将会完整实现一个神经网络。

　　1、图像识别入门：小学级图像分类技术（kNN-k nearest neighbors）

　　　　最近邻图像分类技术：衡量个图片中相同位置像素之间的距离。将距离求总和获得的值作为惩罚函数。值越大说明两张图片距离越远越不相似。该技术不需要训练，只需要将图片依次和训练集中每个图片相互比较，输出像素距离最近的那张图片的标签即可。正确率根据距离计算公式不同在30%到40%间摆动。

　　　　最近邻距离计算方式：最近邻的距离有几种计算方式，包括直接取差值之和、对差值取绝对值（L1 Loss）、对差值取平方（L2 Loss）。本质上没有什么不同。

　　　　kNN:如果取相似度前k高的图片，然后将其标签得投票得结果作为分类结果，就叫做kNN。k Nearest Neighbors。正确率一般在30%左右。

　　　　kNN的超参数优化：kNN有一个超参数（需要认为调整的参数）——k，一般需要从零开始循环，并不断输出每个参数下模型的准确率找到最合适k值。

　　2、线性分类器：SVM向量机以及Softmax

　　　　分类器是一个神经模型中最后一站。但并不一定是整个模型的最后一站分类器和分类器层还是不一样的。但是不管是哪一层，只要是神经网络，一定就需要有一个分类器。因为分类器的功能不仅仅是分类，还包括惩罚函数的生成。在学习时，分类器层是最先接触“错题”的正是分类器使得模型有了输出结果与学习的能力。

　　　　只要是一层神经网络（比如鸟瞰中的卷积层和全连接层），那就一定会配着分类器。可以说，分类器是神经网络层的组成部分。

　　　　线性分类器，顾名思义其分类方式都是线性的，即通过一次函数导出评分。

　　　　假设W是参数，x是样本数据，而b是偏倚参数，那么一个线性分类器的参数包括W和b。线性地计算评分:

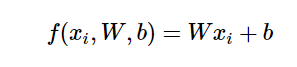
　　　　评分所代表的是该样本是该类的可能性值。如果W是向量，那么就能同时计算多个类的评分，如果W是矩阵，x是向量，就可以同时计算多维数据的多个类的评分。如果两个都是矩阵就可以同时给多个多维数据分类了。实际应用中W一般是矩阵，x一般是向量。

　　　　而不同的线性分类器之间的区别在于——其生成惩罚函数的方式不同。

　　　　SVM的惩罚函数使用公式

　　　　

　　　　L_i是第i个训练样本的惩罚，s_j与s_yi分别表示第i个训练样本对于j标签的评分（对不正确分类的评分）、对本身标签的评分，Δ是阈值，可以手动设置。

　　　　本质上，就是把犯的错误进行量化并求和。

　　　　而Softmax的惩罚使用公式

　　　　L_i是第i个训练样本的惩罚，f_yi代表对正确标签的评分，f_j代表对错误标签的评分。

　　　　本质上，是计算了分类正确率的相反数。

　　　　此外，两种线性分类器的惩罚函数都会需要包含一项额外的惩罚函数：泛化惩罚函数——所有参数的平方和 与一个参数的乘积

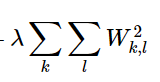
　　　　该参数是一个超参数，可以人为调整。这一项的作用是去峰值，防止出现单个参数对整个模型影响太大。使所有参数均匀地发挥作用，使得模型能够比较好的泛化。

　　3、优化策略：随机梯度下降法Stochastic Gradiant Descent

　　　　完全随机法很蠢，每个周期都随机生成所有的参数，企图随机生成出一个好的模型。很蠢，被否定。准确率跟盲猜差不多。

　　　　局部随机法是从一的点开始在参数空间（每个参数作为一个维度形成高维空间）内布朗运动，稍微聪明点，但是还是很蠢，被否定。准确率比盲猜好一点，15%，但还是不靠谱。

　　　　梯度下降法：取二维参数空间与惩罚函数组成的三维曲面为例，梯度指向的方向就是平面上升的方向，那么取反，就是惩罚函数下降的方向。而这个方向正好就可以给这两个参数以指导。

　　　　因此将参数减去这个梯度乘以一个学习速率即可完成一个周期的训练。

　

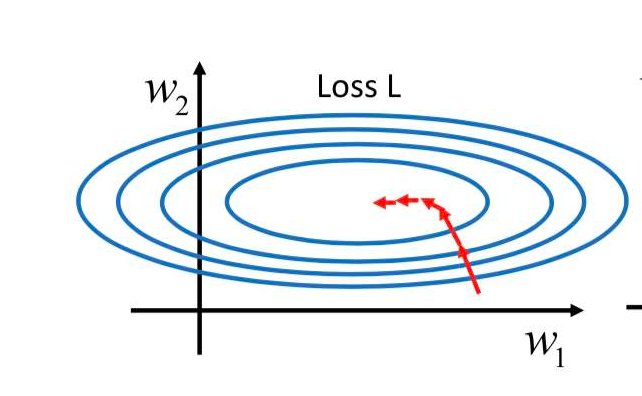
　　　　当前所有神经网络的训练都是使用梯度下降法。随机找一个起点然后开始训练。这就是随机梯度下降法Stochastic Gradiant Descent。

　　　　但是有个问题，那就是不一定能够准确的找到最低点。很有可能会找到一个小坑（局部最优解而非全局最优解）然后就停止了。所以随机找多个一个起点。同步开始训练。这样就能保证有大概率找到全局最优解。

　　　　这就是批量梯度下降法Batch Gradiant Descent

　　　　

　　　　另外梯度下降法一般只适用于惩罚函数为凸函数的情况。反例一般是没有的。因为任何函数在局部都可能成为局部凸函数。

　　　　如果数据太多，那么可以取一小部分，分批次进行训练，这不耽误整体效果，这就是分块梯度下降Mini-batch gradient descent

　　4、优化的具体方式：反向传播Backpropogation以及对反向传播方法的整体把握

　　　　由于神经网络具有多层，而能够直接计算得到梯度的只有最后一层——分类器层。但是前面的神经网络也需要训练。这就需要进行反向传播算法。

　　　　根据链式法则，函数的导数可以分解成复合函数的偏导的连积。

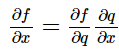
　　　　那么在计算上一层梯度的时候就可以将这一层的参数直接乘上由结果直接生成的梯度矩阵再与上一层的参数矩阵相乘得到。不会收到最终复杂函数形式的影响。

　　　　PS.过去经常使用sigmoid函数作为激活函数，因为其导数的形式十分简洁sigmoid(1-sigmoid)。但是后来被抛弃了，因为这个函数有个致命的缺陷。那就是在数据很大时，函数值会逼近1，这时求导数就几乎没有意义了，这就是众所周知的——数值饱和中毒问题。当然，数据太小也会有这样的问题。所以应该使用ReLU作为激活函数。x是得分。

　

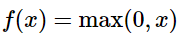
　　　　呃，好像剧透了。那做个标记，这边记录过了。#1

　　　　5、建立神经网络的第一步：建立整体结构（激活函数、神经网络层次架构以及选择）

　　　　　　神经网络就是模拟神经元的活动，众多的参数相当轴突axon，参数为正那就有连接，参数为零那就无连接。贴在人家树突dendrites脸上,数据来了那就是信号，如果超过了阈值那就激发了激活函数activation function形成了输出。

　　　　　　所以仿生呗，那神经网络就需要有这些结构：分类器，激活函数。

　　　　　　分类器就是使用用前面几个单元里面介绍的分类器了。而激活函数就是使用#1处的激活函数了ReLU。此外还有另外几种激活函数，Tanh正切函数，不过毛病和sigmoid差不多LeackyReLU是二进制版ReLU，MaxOUT取最大值。

　　　　　　分类器的作用已经做过笔记了。激活函数的的作用就是根据分类器的输出决定是否要形成信号向下一层输出。

　　　　　　这里课程单独介绍了神经网络的命名习惯。一般来说，包括最终的分类器层在内，有几层神经网络那就算是几层的网络。

　　　　　　最后课程通过数学证明，说，神经网络是万能的。

　　　　6、建立神经网络第二步：准备好数据与惩罚函数（数据预处理、参数初始化、泛化规则、惩罚函数）

　　　　　　数据预处理：第一种方式：用mean把数据中心挪到原点，然后把数据上下界缩放一下。

　　　　　　　　　　　　第二种方式：主成分分析PCA——principle components analysis——利用奇异值分解获得原始数据协方差的正定二次型空间向量基矩阵，取前N列与原来的数据矩阵相乘即可得到前N种最重要的主成分。这种方式，可以将数据中的相关变量合并成一个变量并相应加权，并且能够自动排序获得主成分序列。由此可以大大地降低数据的维度。

# 假设原始数据 X 规模为 [ N x D ]
X -= np.mean(X, axis = 0) # 以零为中心 #2
cov = np.dot(X.T, X) / X.shape[0] # 获得协方差矩阵

U,S,V = np.linalg.svd(cov) # U V均可以作为空间向量基矩阵

Xrot_reduced = np.dot(X, U[:,:100]) 

　　　　　　　　　　　　最后将其进行上下限的整理。规约到同一个数量级。

　　　　　　参数初始化：全零：不行，模型学不动。

　　　　　　　　　　　　小随机数：行，不一定总是好，因为太小了，学起来很慢。

　　　　　　　　　　　　动态矫正Calibrating the variances with 1/sqrt(n).：特别行，将每个参数都初始化成 1/样本数，为了保证不会造成过对称symmetry，一般要乘上一个期望为1的随机数因子进行初始化。

　　　　　　稀疏初始化：局部进行动态矫正初始化，避免对称性。

　　　　　　偏倚量(b)初始化：0.01不错。

　　　　　　批初始化Batch Normalization：新兴的初始化方式，很火特别好http://arxiv.org/abs/1502.03167。但是初学没必要深究。

　　　　　　泛化：实现方式就是前面分类器里介绍的泛化惩罚函数，除了那里记录的L2方式还有L1方式（绝对值）以及抛弃方式（dropout扔掉没用的参数) 。与L2的泛化方式不同。L1和dropout不是让参数均匀地起作用而是武断地扔掉一些参数，这就很有可能会造成最终的参数空间不再包含最优点甚至于偏差很远。因此实际经常使用L2方式。

　　　　　　惩罚函数：由组成神经网络的分类器中的惩罚函数提供。

　　　　7、建立神经网络第三步：训练与监视（梯度检查、健康评估、训练过程监管、参数更新、超参数优化、模型评估）

　　　　　　检查梯度：初步确定应该使用多大的学习速率等超参数。检查参数大小，以及各个变量，避免因为过小或者过大造成数据溢出。确定好合适的泛化参数，不要让参数们被拍成饼。

　　　　　　　　　　   在检查过程中确保不要使用dropout与参数增强。只检查其中几个维度即可。

　　　　　　健康评估：估算一下初始惩罚函数大小。尝试运行一个周期，进行比对。

　　　　　　　　　　　做好警惕不能对任何数据进行度过拟合。

　　　　　　过程监管：通过作图实时监控准确率与惩罚函数的变化情况。

　　　　　　参数更新：主要是学习速率的确定方法。小的模型可以随便自己试几个数。

　　　　　　　　　　　大的模型就需要严格研究了有这些方法步衰step decay,指数衰exponential decay,倒数衰1/t decay，另外还有啥也不管(Vanilla),动量变化量(Momentum update),纳斯特罗动量(Nestorov Momentum),Adagrad,RMSprop,Adam。比较了半天，发现还是RMSprop最好。

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

　　　　　　　　　　　事实上是用了一个动态的梯度平方均值。

　　　　　　超参数优化：一般情况下，多线程进行。多个线程检验不同的超参数，把结果记录一下，然后由主线程找出最好的那套超参数。

　　　　　　　　　　　　超参数优化一般取一部分数据而不是全体进行。并且一般是在一个范围内进行随机选择。范围从大到小，精度从低到高。

　　　　　　　　　　　　此外新兴了贝叶斯超参数优化。Bayesian Hyperparameter Optimization https://github.com/JasperSnoek/spearmint、http://www.cs.ubc.ca/labs/beta/Projects/SMAC/、http://jaberg.github.io/hyperopt/。但是对于复杂卷积网络没啥区别。不看也罢。

　　　　　　模型评估：得到一堆模型然后挑挑拣拣。

　　　　　　　　　　可以通过同模型多种初始化、取准确率排名靠前的模型、同一个模型的不同时间点的快照、平均参数这些方法来得到效果比较好的模型。

　　　　8、一个迷你的神经网络模型代码实现

　　　　　　总体结构：为{输入层-隐藏层-输出层} 共两层神经网络。其中输出层的的神经网络的偏倚量不必要进行梯度下降。

　　　　　　以下代码是可以跑通的（装有numpy），不过在jupyter notebook下运行味道最好

# 进行数据的生成
import numpy as np
N = 100 # 每个类别的样本数
D = 2 # 数据的维度，这里是二维的平面所以数据的维度是2
K = 3 # 种类数
X = np.zeros((N*K,D))# 数据矩阵每一行都是一个单独的样本。一共N*K个样本，每个样本都有D个维度
y = np.zeros(N*K,dtype='uint8')# 每个样本的标签
import matplotlib.pyplot as plt
for j in range(K):# 对所有的K种样本类别
    ix = range(N*j,N*(j+1))# ix将会根据样本种类1，2，3分别选择序列：1..100,101..200,201..300对这些点进行对应的类别标记。
    r = np.linspace(0.0,1,N)# 获得等差数列，作为向径r
    t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # 获得具有最大100x0.2=20度浮动的Θ角度值
    X[ix] = np.c_[r*np.sin(t),r*np.cos(t)] # 获得螺旋散点
    y[ix] = j # 将这100个数据都标记成当前的类别
plt.scatter(X[:,0],X[:,1],c=y,s=40,cmap=plt.cm.Spectral)# 做散点图，参数1，2为x,y轴坐标,颜色用y标记 这里将会展示样本点即训练数据的分布情况
plt.show()

# 神经网络
# 初始化
h = 100 # 隐藏层的尺度
W = 0.01 * np.random.randn(D,h) # 随机生成相对于每个维度总和期望均为1的参数，将第一层网络的参数进行初始化
b = np.zeros((1,h))# 将偏倚参数（常数项）初始化为零
W2 = 0.01 * np.random.randn(h,K) # 随机生成h*K的参数，将第二层网络进行初始化
b2 = np.zeros((1,K))# 将第二层参数进行初始化

# 超参数（训练过程中可以手动改变而且可以进行优化的参数）
step_size = 1e-0 # 学习速率
reg = 1e-3 # 泛化强度。用于参数的泛化规约。

# 梯度下降循环
num_examples = X.shape[0] # 获得训练数据的样本量
for i in range(10000):  # 进行10000次训练

　# SoftMax分类器.线性分类功能
  # 获得所有样本的分类结果, [N x K] 
  hidden_layer = np.maximum(0, np.dot(X, W) + b) # 这里使用的ReLU激活函数 正则化线性激活单元，对线性激活函数进行了小于0时的归零修正。
  scores = np.dot(hidden_layer, W2) + b2  # 将通过第一层的数据再经过第二层分类器获得全样本分类的评分结果
　# 到这里数据就已经完全通过了两层神经网络，接下来就是惩罚函数和梯度下降了
　# SoftMax线性分类器.惩罚函数功能
  # 计算类别的概率,[N x K],通过自然指数函数化归probs的实际意义是将N个样本对K种类别的分类结果全部转换为概率的形式。方便后续的损失函数计算
  exp_scores = np.exp(scores)# 中间表达式
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
  # 损失函数，计算总熵以及反泛化惩罚
  correct_logprobs = -np.log(probs[range(num_examples),y])# 这里的probs数组以批处理的方式形成N * K 个分类结果的概率形式损失。使用了正向的评判
                                                          # 标准。事实上就是判断正确的样本的总标量（probs中存放的就是分类正确的概率型。）
                                                          # 数组中使用双重批处理将会形成一位结果。N*K。将y中 0，1，2类别的分量依次从Probs中取出。
                                                          # 事实上， 就是选择了样本源标签位置处生成的损失值累加。
  data_loss = np.sum(correct_logprobs)/num_examples # 获得预测总损失
  
  # SoftMax线性分类器.反泛化惩罚
  reg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2)# 获得总的反泛化损失。目的是消除样本中的参数峰。
  loss = data_loss + reg_loss # 真正的总损失
  if i % 1000 == 0:
    print ("iteration %d: loss %f" % (i, loss)) # 每进行1000次迭代时输出迭代次数与惩罚

　# 反向传播
  # 通过预测的类别概率矩阵计算梯度
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples

  # 通过反向传播计算梯度
  # 第一组反向传播，通过结果层向第二层参数进行传播
  dW2 = np.dot(hidden_layer.T, dscores)
  db2 = np.sum(dscores, axis=0, keepdims=True)
  # 第二组反向传播到隐藏层
  dhidden = np.dot(dscores, W2.T)
  # backprop the ReLU non-linearity
  # 反向传播到ReLU的非线性结构
  dhidden[hidden_layer <= 0] = 0
  # finally into W,b
  dW = np.dot(X.T, dhidden)
  db = np.sum(dhidden, axis=0, keepdims=True)

  # add regularization gradient contribution
  # 向步进参数中添加上泛化参数
  dW2 += reg * W2
  dW += reg * W

  # 进行最后的参数步进
  W += -step_size * dW
  b += -step_size * db
  W2 += -step_size * dW2
              
              
# 评估参数的准确率
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print ('training accuracy: %.2f' % (np.mean(predicted_class == y)))

　　2号模块：介绍了卷积神经网络。以及一些具体的技巧与注意事项。

　　　　1、卷积神经网络的结构以及卷积层（卷积层次、层次结构）

　　　　　　鸟瞰已经介绍过了，卷积神经网络组成为：输入 - 卷积层 - 激发层 - 缩放层 - 全连接层（放在最后的全连接层被称作分类器层）。英文：INPUT-CONV-RELU-POOL-FC

　　　　　　输入层包含数据。

　　　　　　卷积层CONV，已经记录过，与全连接层FC（FC是标准的神经网络）都是一种神经网络。但是事实上，CONV并不是标准的神经网络。

　　　　　    一个神经网络是两个层之间，所有的参数之间都能两两链接，但是卷积层并不是这样。卷积层在接收上一个层次数据时，每个每个数据点不会同时连接上一层所有的数据，而是仅仅连接一个小区域内的数据Local Connectivity，这个区域叫做接收区receptive field 。这样就更加贴切地模拟了神经元的实际情况（神经元之间不可能总是全连接）。

　　　　　　假设W标志接收的参数个数，F表示接受区大小，P表示边界处空输入个数（填充以0），S表示两个接受区之间的步长。接收之后生成的参数数量就是(W-F+2P)/S+1。比如输入7x7接受区3x3步长1，P=0，那么就会得到同样3 x 3的输出。

　　　　　　卷积神经网络能在形成比较复杂的架构的同时拥有该表规模的能力。

　　　　　　缩放层Pooling layer又称池化层。是一个纯粹用于缩放数据规模的层次结构。可以扔http://arxiv.org/abs/1412.6806

　　　　　　泛化层Nomolization Layer有时候会有泛化层，作用和泛化惩罚差不多。

　　　　　　此外有很多业界的卷积模型:LeNet,AlexNet,ZF Net,GoogleNet,VGGNet,ResNet

　　　　　   需要额外注意的是：每个网络层都要保留好其梯度。每个版本的完整神经网络模型都要做好快照（万一哪天优化着优化着突然学坏了呢(￣_￣|||)）。

　　　　2、解释卷积神经网络与可视化（相似可视化叠层、反卷积、数据梯度、欺骗、人工比较）

　　　　　　（一定程度上）理解自己的神经网络，可以将卷积层的结果、激活函数的结果可视化。

　　　　　　或者用t-SNE方法，将自己模型的想法可视化为云——一堆图，我空间距离近的，模型会说：“俺也一样”。我感觉空间距离远的，模型会说：“俺也一样”。

　　　　　　处理遮掩http://arxiv.org/abs/1311.2901

　　　　　　骗，偷袭，神经网络http://arxiv.org/abs/1412.6572

　　　　3、如何借助面向CV编程技术快速搭建自己的卷积神经网络

　　　　　　分类讨论：

　　　　　　如果我的数据集比他们小，那么不管和他们是否相似，那就训练个分类器层安上就得了。

　　　　　　如果我数据集比他们大而且类似，那就放心继续用自己的数据训练。

　　　　　　如果我的数据集大而且非常不一样，那就重新初始化并训练整个网络。

　　　　　　神经网络界的github:https://github.com/BVLC/caffe/wiki/Model-Zoo

三、尾声

　　　神经网络指的是两个数据矩阵之间的网。不是数据矩阵的某个状态。也不仅仅是指参数。它是由分类器和激发器组成的，就像一块完整的神经组织。