AA5-周期性复习干线
数据结构与算法:
0.散列的实验:在线性开型的散列表实现中。我刚开始错误的认为删除一个元素时只需要将同一个模n同余类下的元素进行相应的移动即可,但是忽略的一个问题——那就是如果其他桶基点的模n同余类没有在本位,而当前删除的模n同余类却进行了位移,将会造成一个或多个空位。而这些空位将会直接导致对应的模n同余类数据损失。最后改正了这一点成功AC(代码可展开):

1 void hashClass::erase(int target){ 2 3 int k=target; 4 int b=search(target); //e的起始桶 5 int count=0; 6 if(table[b]==-1) //如果起始同为空 7 { 8 cout<<"Not Found"<<endl; 9 10 } 11 else if(table[b]==k) 12 13 { 14 table[b]=-1; 15 int i=b; 16 int z=b; 17 int x; 18 do{ 19 i=(i+1)%divisor; //起始桶下一个元素 20 if(table[i]==-1) //如果为空 21 { 22 break; 23 } 24 x=table[i]%divisor; //起始桶下一个元素 的起始桶 25 if(i!=x&&x<=z&&i>z){ //起始桶下一个元素不等于x, 26 table[z]=table[i]; 27 table[i]=-1; 28 // cout<<"把索引 "<<i<<" 覆盖 "<<z; 29 count++; 30 z = i; 31 } 32 else if((i!=x&&i<x&&z<i)||(i!=x&&i<x&&z>=x)) 33 { 34 table[z]=table[i]; 35 table[i]=-1; 36 // cout<<"把索引 "<<i<<" 覆盖 "<<z; 37 count++; 38 z=i; 39 } 40 }while(table[i+1]!=-1&&(i+1)!=b); 41 42 cout<<count<<endl; 43 } 44 45 };
所以,对于新的问题的思考,不能分立地思考,考虑一个种类的元素同时也需要考虑是否会对其他类造成影响。
1.竞赛树:
赢者树,适用于有序的序列要求中,修改和查询操作多的问题。代表性的问题是装箱问题。赢者树的数据结构为二叉树,相对于二叉树的节点,会多一个本次赢者的域,存储此节点的赢者。每一个子树都记录此轮比赛的赢者。根节点记录总冠军。这样,这样的数据结构就能通过节点值直接检索到最小或最大的外部节点处,从而进行修改。当赢者树产生了修改时,需要对路径上从根节点到外部节点的所有节点进行修改。或者到一次必输的节点为止。赢者树的初始化可以从右孩子节点开始,右孩子的父节点一定能够进行比赛。这是完全二叉树的特点决定的。
输者树,是对赢者树的优化,可以比赢者树少一些复杂度。当问题只会修改总冠军时会比赢者树效率高很多,因为,输者直接记录在节点处,子节点的信息不会被赢者的信息覆盖,可以更快地完成树地更新。
2.搜索树:
搜索树也是一种二叉树,局部特征为:任何一个节点包括根节点在内,左子树的关键字大小于根节点,根节点小于右节点。这样,当查找一个元素的时候,只需要通过判断节点值的相对大小就就可以一路深入到叶子节点找到目标元素。插入时,只需要沿着相同的路径下潜最后插入到合适位置即可。
但是如果想要查找中位数或者顺序第n位呢?可以在节点处增加一个域,标记的内容为该节点左子树的size这样就可以利用这个值作为检索工具,快速地找到顺序第n个元素。这便是索引搜索二叉树。
当二叉搜索树删除的时候,如果删掉了一个存在左右子树的节点,会需要给左右子树一个交代。怎么办呢?注意到空间位置上,被删除节点正下方的叶子节点正好比左子树根节点大,比右子树的根节点小,因此把这个叶子节点拿过来就能补上空位了。
在应用上可以在直方图的频数统计上加速过程。首先,当将数据插入二叉搜索树,然后利用二叉搜索树的前序遍历的有序性,将其顺序输出,将极大地方便统计。
应用上还可以用于装箱问题的最优适配法,本质是排序。
还可以用于布线的交叉平衡。如何在上下两个区域中分布相等数量的交叉点?
首先注意每一对逆序数都代表着一个交叉点。所以将C序列生成一个搜索树,完事后中序遍历得到一个序列,最后关系替换,就是中路的布线序列。
3.平衡搜索树:
平衡二叉树是一种不会“畸形”的二叉搜索树。平衡二叉树的任意一个左右子树高度差不会超过1,这就意味着,这种二叉树会保持logn的高度,同时也就意味着稳定的logn的搜索复杂度。
搜索,与搜索树是一样的。
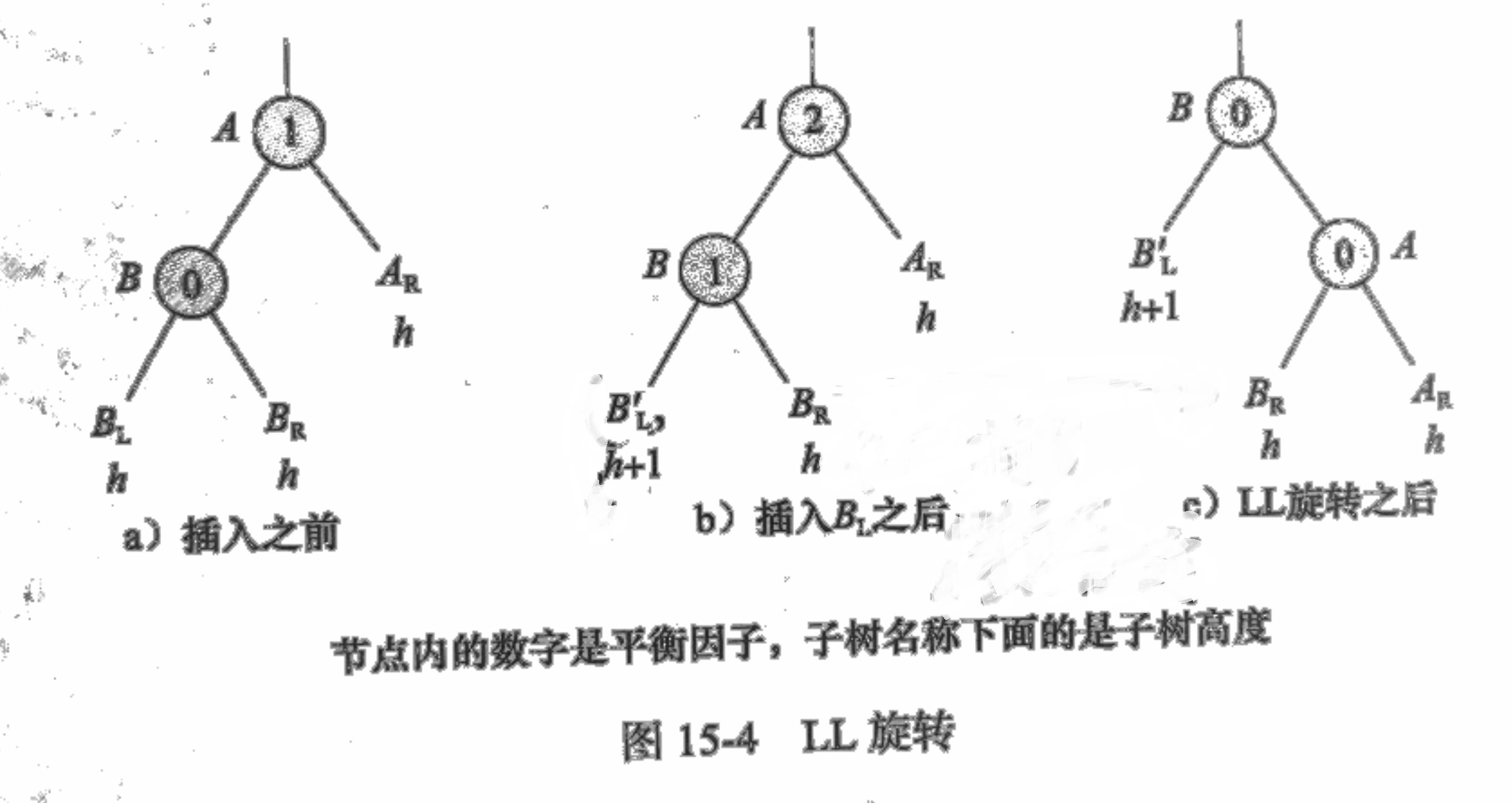
平衡二叉树的插入,会牵扯到不平衡的问题。如果不平衡,会导致四种不平衡LL,LR,RL,RR,由于对称性,事实上只有两种不平衡。LL是由第一个不平衡节点的左左子树高度增一导致的。此时,左右子树与右子树的高度相同,而左左子树比他们都高1,那么只需要将左右子树和右子树放到同一高度,并且将左左子树进行修剪即可。具体来说,首先需要将LL,L,A(首不平衡节点),R连成一条链,然后将LL上移,R下移,L成为新的中心,然后将A的父节点接到L上方,断开的LR接到A左子树位置。至此便完成了一次LL翻转。新的节点中,L作为根节点,平衡因子为0。实现了平衡。如果是LR型,是由第一个不平衡节点的左右子树导致的,此时左右子树比左左子树和右子树均高一。此时LR的两个子树LRL,LRR中一定有一个高度为h,一个为h+1,而LL,R均为h,此时需要将C转移到L和A之间,然后将左右子树分别接到L的右子树和A的左子树,这样高度为h,或h+1的节点LL,LRL,LRR,R就都在同一起点处了,至此,达到新的平衡,平衡因子可能为1,-1,0完成了LR翻转。
LL: LR:

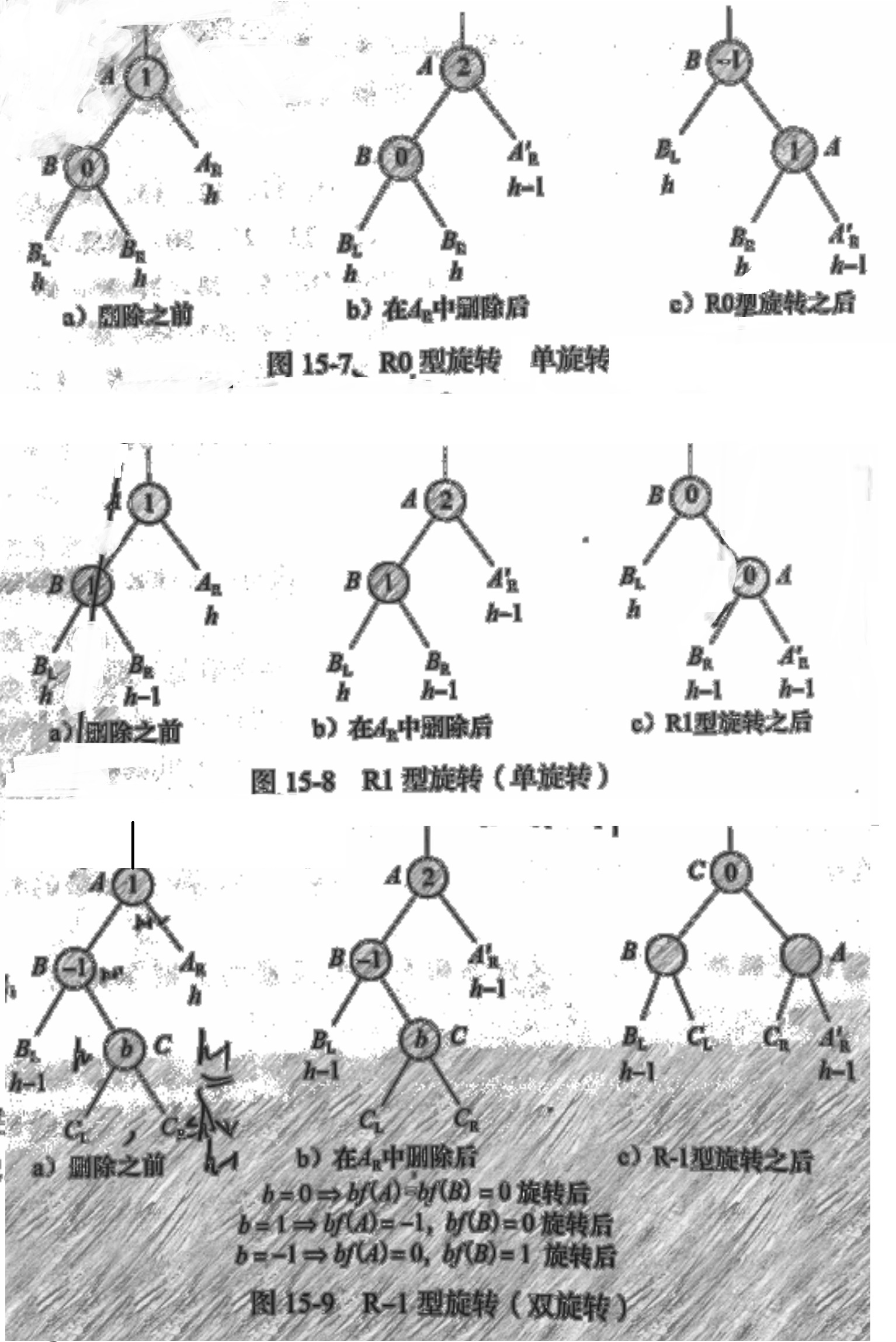
删除操作中,分为R0,R1,R-1三种情况,对称的操作有L0,L-1,L1(对称的操作正负号相反)。R0是指A=1时,左子树L=0,删除右子树导致A=2。参考上面的平衡策略,只需要将LL,LR,R放到同一高度就好,所以还是链式右滑,L替换A的位置,重新连接,OK。R1也是一样的。R-1 的时候,形式类似于插入时的LR旋转,因为h+1的子树LR并不在可以滑动的链条上,所以需要把LR为根节点的树分解掉,LR替换A,A链右下下滑,然后LR的左右子树分别接到左右链的空位,完成翻转。
B-树
B-树,主要指多阶B-树。特点为根节点至少两个孩子,根节点外所有内部节点至少有[m/2]个孩子,并且所有节点都在同一层。
在内部节点中,相邻元素有序,与孩子结点的关系类似于搜索树。
每个节点最多存储m个元素,任何相邻元素之间都可以有一个指针指向孩子节点,这个指针的特点为,孩子节点的所有元素大小均在这两个相邻元素之间。
这也是一个类似平衡树的数据结构,其应用特点是可以处理更一般化的实际问题中的搜索要求。搜索时按照搜索树的思想进行即可。
插入:插入时,按照搜索方法找到位置完成插入,如果已经满了,那么首先,将已满的元素的中位数之一向上发送成为父节点中指针的左或者右侧元素,然后将两侧元素拆分为两组分别接在该元素的左右指针处。如果发送完后仍然有溢出则进一步进行拆分重构。
删除:如果删除时破坏了结构,需要首先尝试将附近的节点进行合并,如果合并后高度出现差距则尝试将父节点的父节点向下遣送,尝试降低整体高度。这个过程中可以尝试合并祖父节点与父节点的右侧节点,如果能成则将附近合并完成的节点向同高度节点的父节点进行合并。最后完成合并。
5.图:
在离散数学中早已经学习过了图的概念。现在需要通过代码建立图的数据结构以及应用的算法。
首先图可以通过邻接矩阵来进行描述,无论是有向图还是无向图,都可以用矩阵的0,1值来代表是否通达以及边的方向。当我们需要找到一个路径时我们完全可以通过二重循环遍历所有的关系,最后再套一层循环找到路径。
但是有了稀疏矩阵的经验,我们知道,当图的顶点数多一些的时候,数据规模莫很容易就会变得非常大,这时候这种n3的复杂度无异于彻底断绝了这种数据结构进行实际问题应用的可能性。
因此,大家采用了类似于稀疏矩阵三元组的思想。只记录有用的信息。由此诞生了图的最常出现的数据结构:
邻接数组与邻接链表图:
图的数据结构由几个方法以及数据成员——邻接数组/链表,顶点个数,边数组成。邻接数组/链表存储的是该位置的顶点所能够通达的点。
如果是加权图,则邻接数组/链表中,还会多出一个域——权值。
图的遍历问题,很明显如果一个图是联通的,那么通过深度搜索或者广度有限搜索,能够一次性完成全部顶点的遍历与标记。但是如果并不完全连通就需要从头开始对每个未标记的节点作为起点进行搜索并标记。回到表层后跳过已标记的节点继续将所有未标记的节点遍历完成。
在图的遍历过程中显然是树的结构,这就是生成树。
利用贪心算法,可以将搜索算法进行改进,形成最小生成树/最大生成树。
数据库系统概念:
1.最近来到了BC范式,第三范式,第四范式的分解算法。第一范式没有存在感,第一范式只有一个特征——原子性:元胞不可分。主要重点在习题。在明白算法的基础上,看看习题解法会事半功倍。
计算机组成原理:
1.指令系统以及指令格式的设计:
指令系统主要内容为指令格式以及寻址方式。
指令格式粗略可以表示成 OP[+M[+R/A[+R/A]]] 有0,1,2三种地址指令,最多2M种寻址方式,R/A 个寄存器/形式地址。
实际设计时,按照题目要求OP是否可变,像之前存储器扩展的第二步列地址范围一样把各种指令的地址范围列出来即可。
如果OP可变则OP = 机器字长 - 其他一切位数
如果不可变则 OP = 机器字长 - 最长指令的除OP指令之外的位数
2.寻址方式:
立即数寻址 operand = A 零次主存,数据范围 [A] bit (补码)
直接寻址 operand = adress(A) 一次主存,寻址范围 [A] bit
隐含寻址 operand1 = address(A) 一次主存,寻址范围 [A] bit
operand2 = ACC 不主存,一次寄存器,数据范围, [ACC.size()] bit
间接寻址 operand = address(address(A)) 两次主存,一次寄存器,寻址范围 [主存数据宽度] bit
寄存器寻址 operand = Ri 零主存,一次寄存器,数据范围 [寄存器数据宽度] bit (补码)
寄存器间接寻址 operand = address(Ri) 一次主存,一次寄存器,寻址范围 [寄存器数据宽度] bit
基址寻址 operand = address(BR/Ri + A) 一次主存,一次寄存器,寻址范围 [寄存器数据宽度] bit
偏倚范围 [A] bit (补码)
极限寻址范围 [寄存器数据宽度+A] bit (高低位交替存储,极限扩展范围)
基址寻址中Ri内容不可变。BR为专用寄存器。
变址寻址 operand = address(IX/Ri + A) 一次主存,一次寄存器,寻址范围 [寄存器数据宽度] bit
偏倚范围 [A] bit (补码)
极限寻址范围 [寄存器数据宽度+A] bit (高低位交替存储,极限扩展范围)
变址寻址中Ri内容可变。IX为专用寄存器。
相对寻址 operand = address(PC + A)一次主存,一次寄存器,寻址范围 [PC] x [A] bit
偏倚范围 [PC] bit (补码)
适用于数组问题以及顺序执行的程序。
堆栈寻址 operand = ACC = stack.pop() 一次堆栈,如果是软堆栈则涉及多次主存以及寄存器,如果是硬堆栈则仅涉及多次寄存器。寻址范围 [堆栈数据位数] bit
3.RISC —— reduce instruction set computer 顾名思义,化繁为简,由简及繁。
4.计算机组成原理实验:
实验九:
BUSLINE 大粗线怎么用。首先大粗线可以直接拉出来,接到output上,不过output的命名需要有形如q[7..0], p[0..7]这样的形式。也可以将busline拉出来,单独给busline一个名字就可以单独拉出来busline中的其中几条了。
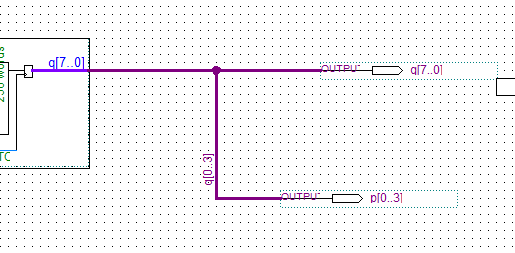
如果想要完全分开可以在busline上引出 Node line 就是那种细线。
只需要在细线上标明是busline中的哪一条即可。

编译出错——cannot sign more than one....数据总线无法汇总。
软件问题,编译不允许多个赋值。所以,数据总线那边可以并一下。
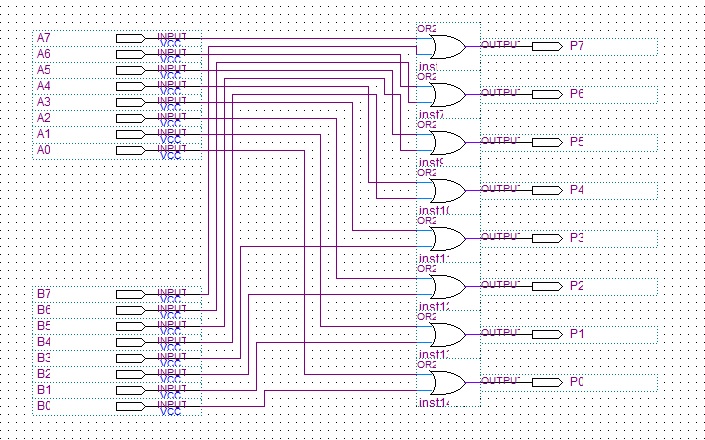
或者busline之间也可以并:经过实测确实可以。
实验十:
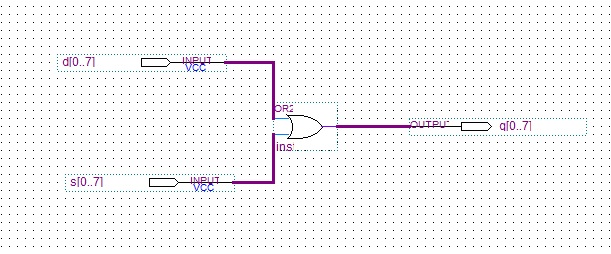
这是一个时序加法器。四位数出在两次上升沿依次输入。如果输入不变而不断进行时钟循环,则进入累加模式。
输入包括四位数据,还有K,这里可以直接利用K同时完成取反加一。
输出包括四位数据,两位符号位,一位溢出判断。符号位作为高位直接运算即可。溢出位比数据为高一位,每次数据位溢出都会输出1。否则输出0。
实验十一:
。。。略
实验十二:
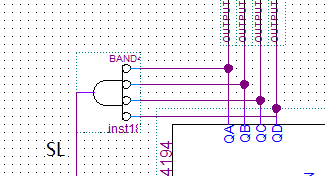
emm...实验指导手册里的SL接Qa可能不对。应该是这样的。否则不能做到单波。
实验十三:
UIR- 指令寄存器 UPC- 计数器用于顺序索取指令地址。注意时序线对于URD和UPC是反相的。目的是防止速度过快导致数据丢失。
实验十四:
综合实验中实验指导手册上的UIR标记不清晰,应该是这样的:
23...20 ... 7 6 5 4 3 2 1 0
四位数据 CPR0 CPR1 CPR2 LM DM RM C0 K
概率论与数理统计:
1.数字特征与大数定律:
二元正态分布很好记的。其实就是1/2πσ1σ2√1-ρ2 exp{ -1/2 [(X-μx/ 1-ρ) 和 (Y-μy/1-ρ)的 完全平方公式] }。
期望,方差之间常用公式:DX = EX2 - (EX)2.
协方差的方差之间的常用公式: DX +- Y = DX + DY +- 2Cov(X,Y)
Cov(X,Y) = EXY - EXEY
协方差(数学期望)与方差,相关系数之间的关系:Cov(X,Y) = ρx,y √DX√DY
数学期望开括号很方便。
很好用的公式。。。∑ (qi)' = (∑qi)' = (q/1-q)'=1/p2。。。甚至于对于高阶中心矩,都能够轻松解决,只需要把导函数的阶数拔高一些。
大数定律:
切比雪夫大数定律:
期望有限,方差有界,期望之和 ——> 之和的期望。
伯努利大数定律:
二项分布期望趋于np
辛钦大数定律:
独立同分布, 期望之和 ——> 之和的期望。
中心极限定律:
独立变量之和的概率密度可以标准化为ф函数。
2.数理统计
卡方分布:相互独立的2阶中心矩之和的概率密度函数。所有中心矩均有X ~ N(0,1)
X ~ χ2(n) => Eχ2 = n, Dχ2 = 2n
X ~ χ2(n) ,Y ~ χ2(m) => X+Y ~ χ2(m+n)
t分布:
N(0,1) over 一个 Y~χ2(n)分布的标准差形式。
T = X / √ Y/n
参数由χ2分布的参数决定,称之为自由度。
T ~ t(n) => E(t(n)) = 0 ,D(t(n)) = n/(n-2) ( n > 2 )
n ——> ∞时
T ——> N(0,1)
t(n) = F(1,n)
F分布:
X~χ2(m)分布的标准差形式 over Y~χ2(n)分布的标准差形式。
F = √X/m / √Y/n
EF = n/n-2
DF = n2(2m+2n-4)/(m(n-2)2(n-4))
F(m,n) = 1/F(n,m)





