[JSOI2004]平衡点 / 吊打XXX

洛咕

题意:如图：

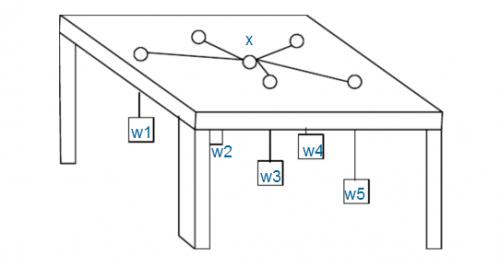
有n个重物，每个重物系在一条足够长的绳子上.每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结.假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦.问绳结X最终平衡于何处.注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处.\(n<=1000\).

分析:模拟退火的入坑题???

先放两篇不错的博客,一个重理论,一个讲实现.

模拟退火的玄学真的没什么好讲的,反正各种参数不断改就行,样例过不去也要试着交一发.实在不行,重构代码也是个不错的选择.模拟退火的玄学,还有输入(\(cin\),\(scanf\),快读都会有不同的效果),数组和结构体存东西也有不同的效果......反正一切不同的东西,都可能使答案改变.所以什么本机AC,提交WA;本机WA,提交AC的事情就多了去了.不论什么写法,不论什么参数勇敢尝试就行(听说很多人就是享受这种乱调试的快感???).

回到本题,根据物理学知识就是要求\(\sum_{i=1}^ndist(x,i)*w[i]\)的最小值.其中\(x\)表示绳结的位置,\(dist(x,i)\)表示绳结和洞口之间的距离,\(w[i]\)表示重物的重量.

知道要求什么东西以后,就可以根据模板不断地调试了.

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#define ll long long
using namespace std;
inline int read(){
    int x=0,o=1;char ch=getchar();
    while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
    if(ch=='-')o=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*o;
}
int n,totx,toty;double ansx,ansy;
struct node{int x,y,z;}a[1005];
inline double calc(double x,double y){//计算当前的答案
	double cnt=0;
	for(int i=1;i<=n;++i){
		double xx=x-a[i].x,yy=y-a[i].y;
		cnt+=sqrt(xx*xx+yy*yy)*a[i].z;
	}
	return cnt;
}
inline void mnth(){
	double T=2003,eps=1e-14;//这两个东西可以尽情改
	while(T>eps){
		double nowx=ansx+(rand()*2-RAND_MAX)*T;
		double nowy=ansy+(rand()*2-RAND_MAX)*T;
//rand()*2-RAND_MAX可以得到[-RAND_MAX,RAND_MAX]之间的数
		double delta=calc(nowx,nowy)-calc(ansx,ansy);
		if(delta<0)ansx=nowx,ansy=nowy;
		else if(exp(-delta/T)*RAND_MAX>rand())ansx=nowx,ansy=nowy;
		T*=0.999;//0.999也可以尽情改,最好在[0.95,0.99]之间
	}
}
int main(){
	srand((int)time(NULL));n=read();
	for(int i=1;i<=n;++i){
		a[i].x=read();a[i].y=read();a[i].z=read();
		totx+=a[i].x;toty+=a[i].y;
	}
	ansx=(double)totx*1.0/n;ansy=(double)toty*1.0/n;//先猜一个较优值
	mnth();printf("%.3lf %.3lf\n",ansx,ansy);
    return 0;
}