博弈(game)
前言
这题要是放NOIP说不定就让我退役了
题目
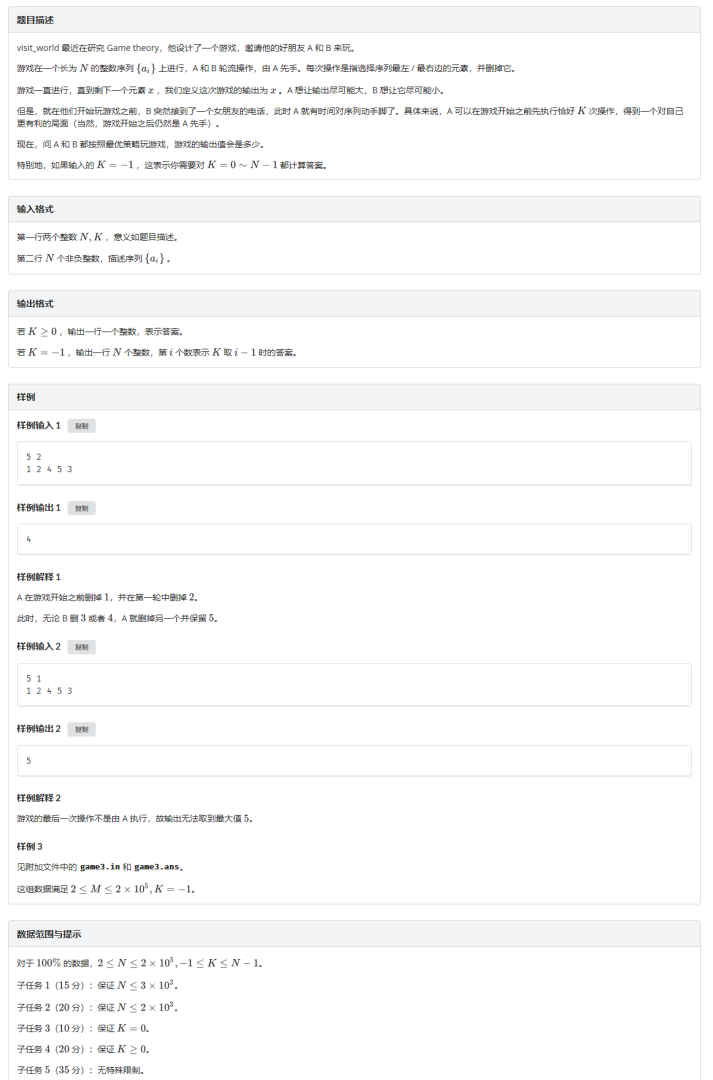
讲解
为了方便，我们令最终剩下的数为\(s\)
part1 35pts
首先我们用记忆化搜索轻松写出\(O(N^2)\)的算法
定义\(dp[w][i][j]\)表示此时左端点为\(i\)，右端点为\(j\)，此时是\(w(0/1)\)人取的时候的最优取值
代码就不给出了
part2 45pts
我们考虑\(K=0\)小B没有女朋友的时候答案应该如何快速求出
考虑分奇偶讨论
1.如果\(N\)为奇数
\(s\)一定出自中间三个数，令他们依次为\(t_1,t_2,t_3\)
考虑如果答案不是出自中间三个数
- 小A想取左边或者右边的数，这样一定对小B不优，小B就会在对面取数，中间的数始终不变，答案一定在中间三个数中产生
- 小B想取左边或者右边的数，这样一定对小A不优，从第三次取数开始，类似的，小A也会在小B的对边取数，这样答案也一定在中间三个数中产生
当最后剩下\(t_1,t_2,t_3\)三个数的时候，一定是小A取数，如果\(t_2\)最小，那么小B一定可以使它被取到
如果\(t_2\)不是最小，小A自己不可能取走\(t_1,t_3\)中一个最大的数，他一定会取走最小的数，剩下一个次大值和最
大值，而小B一定会取走最大值，那么\(s\)即为次大值
2.如果\(N\)为偶数
类似的，\(s\)一定出自中间的\(t_1,t_2\)两个数
此时轮到小A取数，取走最小值，剩下最大值
于是我们就可以\(O(1)\)求出\(K=0\)时的答案了
我称这个结论为中心论
part3 65pts
笔者在考场上就只码出了这个部分分，结果艹过了70pts...
明显part2推论还可以拓展为求剩下区间为\([l,r]\)的时候，小A先取数时的\(s\)
对应代码即为：
int Get(int l,int r)
{
if(l == r) return a[l];
if((r-l+1) & 1)
{
int t1 = (l+r-1)/2,t2 = (l+r-1)/2+1,t3 = (l+r-1)/2+2;
t[1] = a[t1]; t[2] = a[t2]; t[3] = a[t3];
if(t[2] < t[1] && t[2] < t[3]) return t[2];
else {sort(t+1,t+3+1);return t[2];}
}
else
{
int t1 = (l+r-1)/2,t2 = (l+r-1)/2+1;
return Max(a[t1],a[t2]);
}
}
当然这部分的代码也可以替换part1的记忆化搜索，毕竟这是\(O(1)\)的查询，对于每个\(K\)求答案时可以做到\(O(N)\)，共\(O(N^2)\)
我们对于每个\(K\)可以\(O(N)\)枚举提前取数区间求出
共\(O(N^2)\)，如果\(K\ge 0\)，即为\(O(N)\)
part4 100pts
现在我们考虑拿走边上的数会造成什么影响
由于我们分奇偶讨论，拿走奇数个的时候会对奇偶性造成影响，而奇偶性不同的时候求\(s\)的方法不同，不能合起来讨论，所以我们试图分析拿走偶数个的时候会发生什么
考虑拿走两个数
如果一边拿走一个数，中心不会发生改变！所以\(s\)并不会改变！
如果单边拿走两个数，中心发生偏移，但是偏移不多，我们可以用两次\(Get\)操作求出这左右两种取数后的\(s\)，与前一种取数方案的\(s\)取一个最大值，即为当前\(K\)的答案
于是可以\(O(N)\)递推
但是注意，当\(K=N-1\)的时候，此时我们的中心论已经不成立了，因为所有数都可能成为答案，需要特判
代码
int Get(int l,int r)
{
if(l == r) return a[l];
if((r-l+1) & 1)
{
int t1 = (l+r-1)/2,t2 = (l+r-1)/2+1,t3 = (l+r-1)/2+2;
t[1] = a[t1]; t[2] = a[t2]; t[3] = a[t3];
if(t[2] < t[1] && t[2] < t[3]) return t[2];
else {sort(t+1,t+3+1);return t[2];}
}
else
{
int t1 = (l+r-1)/2,t2 = (l+r-1)/2+1;
return Max(a[t1],a[t2]);
}
}
int ans[MAXN];
void solve_all()
{
ans[0] = Get(1,n);
ans[1] = Max(Get(1,n-1),Get(2,n));
//初始化递推边界
for(int i = 2;i < n;++ i) ans[i] = Max(ans[i-2],Max(Get(1,n-i),Get(1+i,n)));
//O(N)递推，从i-2的状态推过来
for(int i = 1;i <= n;++ i) ans[n-1] = Max(ans[n-1],a[i]);
//特判，因为 "中心论" 不适用了
}
void solve()
{
if(k >= 0)
{
int len = n-k,Ans = 0;
for(int i = 1;i+len-1 <= n;++ i)
Ans = Max(Ans,Get(i,i+len-1));
Put(Ans);
//当然这并没有必要，只是常数优化
}
else
{
solve_all();
for(int i = 0;i < n;++ i)
Put(ans[i],' ');
}
}
int main()
{
// freopen("game3.in","r",stdin);
// freopen("mine.out","w",stdout);
n = Read(); k = Read();
for(int i = 1;i <= n;++ i) a[i] = Read();
solve();
return 0;
}
个人代码有些冗长，如果你不想看的话可以康康下面的std
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int n,k,a[N],ans[N];
int gt(int l,int r)
{
int mid=(l+r)/2,len=r-l+1;
if(len&1)return max(min(a[mid-1],a[mid]),min(a[mid],a[mid+1]));
return max(a[mid],a[mid+1]);
}
int main()
{
// freopen("game.in", "r", stdin);
// freopen("game.out", "w", stdout);
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
ans[0]=gt(1,n);ans[1]=max(gt(1,n-1),gt(2,n));
for(int i=2;i<n;i++)ans[i]=max(ans[i-2],max(gt(1,n-i),gt(i+1,n)));
for(int i=1;i<=n;i++)ans[n-1]=max(ans[n-1],a[i]);
if(k>=0)printf("%d\n",ans[k]);
else for(int i=0;i<n;i++)printf("%d ",ans[i]);
return 0;
}
