杂题乱做
CF1572C
对于一段区间\([l,r]\),全染成\(c_l\)一定是不劣的,因为不染成\(c_l\)就要把\(c_l\)染成别的色
设\(f_{l,r}\)表示一段区间染成\(c_l\)的最小次数,那么有转移\(f_{i,j}=\min(f_{i,k}+f_{k+1,j}+[c[k]!=c[k+1]])\)
朴素转移代价较高,发现题目一个条件是每个颜色不超过20个,大胆猜测只有后面\(c_k=c_{k+1}\)时才有转移
事实上确实是这样,把颜色和\(c_i\)相同的作为分界点,如果存在一个分界点分成的段被隔成两部分,那么可以把右边给左边,这样一定会少一次让右边变成\(c_i\)的操作,至多多一次左右统一颜色操作,所以不劣,可以感性理解
另外还要算上转移点\(f_{i+1,j}\),因为颜色相同可能不存在
CF1572E
来积累一个三角形面积公式
应该要满足三个点是逆时针的顺序,好像是二阶行列式法
这个题输入给出的点就是逆时针的,所以可以直接用
二分答案面积,然后区间dp来check,二分一个\(mid\),\(f_{i,j}\)表示一段里的最多能分成的面积大于等于\(mid\)的块数,\(g_{i,j}\)表示这个区间里最大剩下的面积,枚举分界点转移,\(f_{i,j}=\max(f_{i,k}+f_{k,j}+[g_{i,k}+g_{k,j}+S(i,k,j)>=mid])\)
如果后面的条件成立那么贡献会多1,这个时候转移成功那么新的\(g\)要置0,否则\(g\)不变,可以压成一个pair转移
答案合法就是\(f_{1,n}>k\),因为要分\(k+1\)块
upd:好像dp之间有一个地方不太清楚
注意剩余部分必须以\(l,r\)的连边为一条边,这样才能转移
CF1578L
他走的路径一定是原图的最大生成树,相当与他变胖就会导致树上可能断边
为了全吃完,他一定是在断掉最短的边之前,先把其中一棵子树上的吃完,然后再去另一个子树里吃
设子树里的答案是\(an\),子树权值和\(s\),那么这个过程答案可以更新\(\max(\min(an_x-s_y,w-s_y),\min(an_y-s_x,w-s_x))\)
这个过程可以用Kruskal 重构树维护,在求生成树的时候建出来,并查集维护,由于重构树的根一定是最后连接的边,所以是当前最小的,于是就很方便的直接做了
CF258D/AGC30D
dp方式很好,直接设\(f_{i,j}\)为\(i,j\)构成逆序对的概率,每读入一个数对考虑对逆序对的贡献,期望线性性
转移是每当一个数对读入,他们之间构成的概率就恒是0.5,因为大小是严格的
其他所有的数构成的概率\(f_{t,x}=f_{t,y}=0.5\times (f_{t,x}+f_{t,y})\)
CF这个题保证了排列,所以\(f_{t,x}=f_{x,t}\),AGC的题不保证是排列,所以还要\(f_{x,t}=f_{y,t}=0.5\times (f_{x,t}+f_{y,t})\)
从本质dp的思路还是再次出现,遇见了不能再一筹莫展
CF325E
构造题,比较神,想了一个小时也没有什么具体思路
哈密顿回路是NP,但本题这个性质使我们可以做
首先如果\(n\)是奇数肯定无解,因为这样\(2k+1\)和\(2k\)就都会被\(k\)转移到,不合法
合法时发现\(i\)和\(i+n/2\)等价,都可以转移到相同的两个节点
那么可以调整,每次先假定一个向\(i*2\),一个向\(2*i+1\)连边,这形成了若干个环
每次如果一对节点不在一个环内就互换他们的指向节点,最终答案不唯一,但一定有合法解
主要是没往同余想,老想二叉树的事了,还是做题少
CF338D
这个表格全是gcd,要求\(a\)在表格中一行出现过
一行\(x\)都相同,显然应该满足\(x=lcm (a_1,a_2,a_3……)\)
于是先求出来\(lcm\),发现\(x\)一定是他的整倍数,选择1倍的时候限制更少,因为如果选择\(k\)倍还要满足\(gcd(k,y)=0\),增加了限制,答案不会变优,于是我们现在考虑\(y\)的限制
对于每个\(y\)来说,其实就是\(a_i \mid y+i-1\),得到这样若干个,所以直接上扩展CRT解
解出来看是不是在格子里,最好往回带入验证一遍
CF317E
依然是构造,但其实不难
如果某个时候公主和影子都走到了一堆树外面,这样公主就可以把影子向里怼到树上
都在里面的情况,二者不连通则无解,否则有解
让公主一直跟着影子走最短路,然后记录公主的移动方案移动影子,如果走出去了那就用上面的方法,否则就会在里面追上
可以证明二者之间距离不会增加,所以最后要么出去要么追上,不会死循环
但是貌似不太好写的样子,于是就胡完了
CF297E
这种看起来很乱很迷的计数题,一般方法是把状态抽象成几个模型
这道题首先要看懂题,那么会发现在只考虑三条弦的情况下,图的情况只可能有下面5种:
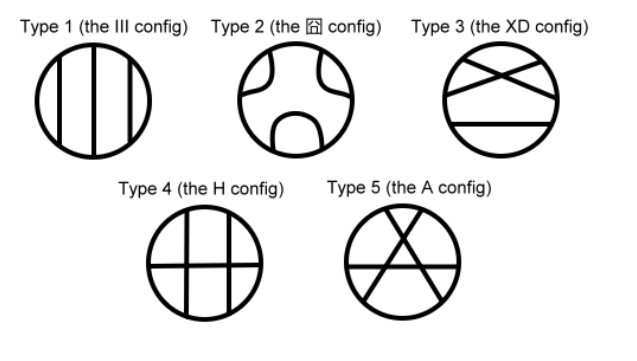
事实上只有2和5的情况合法,直接算不太好算,所以用总的减去不合法的容斥掉
总的显然是\(C^3_n\),设\(l_i,r_i\)分别为一条线左边,右边和他不想交的弦数,假设我们能算出来
那么第一个可以枚举每一个弦,贡献是\(\sum_{i=1}^n l_i\times r_i\)
第3,5类有相同的特点,依旧枚举每条弦,其实他们的方案就是相交弦数乘以不想交弦数
即为\(\sum_{i=1}^n (l_i+r_i)\times (n-l_i-r_i-1)\),不相交的减去他自己
于是我们只用算出\(l_i,r_i\),发现这里的\(x,y\)坐标满足一定关系,所以是个二维偏序
CF273D
奇怪的dp,开始依旧没看懂题
脑补选出格子的形状,他的左边界先减后增,右边界先增后减
于是可以设\(f_{i,j,k,p1,p2}\)代表第\(i\)行,左右分别\(j,k\),左边,右边能否再扩展的方案数,后两维\(0/1\)
行的一维可以滚掉,统计答案的时候每次钦定下边一直这么选拉下去就行
转移理应要前缀和,但还有更nb的方法。每次注意转移顺序,转移的时候一次只更新下一个,然后一路平推
这个技巧感觉很妙,尝试在别的题也用一下
CF338E
首先把右面的排序,然后贪心让左边小的配大的,大的配小的
把\(b_i\)转化成\(H-b_i\),那么就是\(a_i>=b_i\)的匹配
在值域上离散化之后搞,每次在对应的\(a_i\)减1,对应的\(b_i\)加一
那么有匹配的条件是所有位置的前缀和都大于0,表示可以选足够的\(a_i\)匹配\(b_i\)
线段树维护,每次区间修改,查询全局最小值即可
CF1580D
翻译成人话就是,子序列长度x子序列之和-每对点之间的最小值之和,然后简单倒一下柿子

这玩意像极了树上两点之间距离,考虑到树上面转化
最小值显然是笛卡尔树,而贡献的形式可以转化为边权是权值的差
所以就是树上\(m\)个点两两距离最小,树上背包子树合并即可
注意这里每次合并的时候贡献是按照一条边的贡献次数累计的,这样比较好算


