模拟7 T3 寿司题解
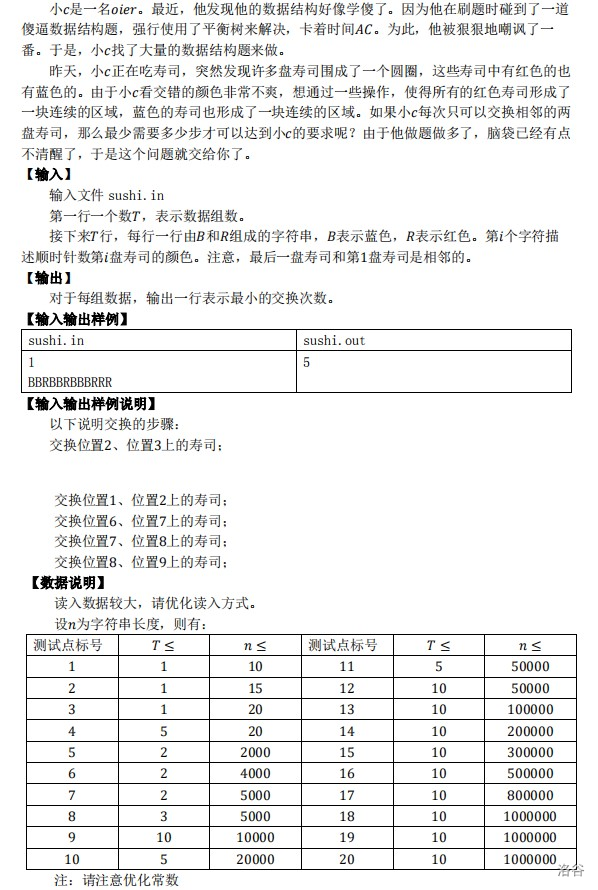
题目要求可以转化成一个01串，让通过最少次数把序列变成中间是0，两端是1；
首先我们可以考虑一些性质：
最优解一定是每次操作都把0和1交换
这个很好理解，如果你交换同一种东西，跟没换一样
这个题卡就卡在他是一个环，由于可以两头交换，所以不好处理，我们的做法是破环为链：
对于整个环，在最优解情况下，一定有两个相邻的位置没有被交换过
如果所有相邻位置都换过，那么他就换回去了，也是无效操作，所有我们可以枚举这个点作为断点，把环视为n个序列
断点确定后，我们设置一个目标状态，就是是一种颜色（0或1）全部靠边（考场上我想的是让一种颜色靠到中间，但这样不好维护，也不好优化）
假如我们让0靠到两边，那么问题就变成：每个1靠到两边的操作次数之和
那么再给一个结论：
每个1靠到左边的花费是他左边0的个数，靠到右边是他右边0的个数
我们如果只考虑一个点的话，他要走到最左边，左边已经有一些1了，他要走的就是左边0的个数
那么现在我们就有了一个n2的暴力：
先预处理出2n长度的链的0前缀，后缀和，然后对于每段n长度的链，对其中每个1比较他走到左边和右边的花费，取min累加贡献，再对每个链的答案取最小值就行，这样有40分，前提是少用几个memset或者把数组开小!!
我们考虑优化，我们发现最优决策好像是有分界点的，对于一条n的链，一定是存在某个点，在左边的点都靠到左边，右边的点都靠到右边，这个其实很好想，哪里0少去哪里嘛，所以我们只要找到这个分界点，然后求出前面所有1靠到左边的贡献，后面所有1靠到右面的贡献就行
怎么办？预处理前缀和的前缀和
我们把1之前到i的所有0数量记为sumb[i],把
从1到i之间所有1的花费记为sum[i],我们可以看出来sum就是前缀和的前缀和
for(int i=1;i<=2*n;i++)
{
sumb[i]=sumb[i-1];sum[i]=sum[i-1];sumr[i]=sumr[i-1];
if(a[i]=='B')sumb[i]++;
if(a[i]=='R')sum[i]+=sumb[i-1],sumr[i]++;
}
蒟蒻不会用三目运算符，请见谅
sumr是1到i所有1的个数，一会要用。注意花费是之前的0个数，所以要减1
后缀和什么的也一样，下面就是如何求出差分之后的值了。
因为我们枚举到2n，现在想求从i到j的前缀和，我们看上面这个递推柿子，可以想到
把i到j的1靠到i的花费=把1到j靠到1的花费-把1到i靠到j的花费-i之前的0个数*i到j中间的1个数
就是 $$ans=sum_j-sum_{i-1}-sumb_{i-1}\times(sumr_j-sumr_{i-1}) $$
我们把i当成第一位，前面所有的0都被多算了，中间有几个1就多算了几次，减去
那么我们只有最后一个问题：分界点到底在哪？？？
我们当然可以二分，nlogn卡常就可过，但是他可以On：
记得上面的一句话：哪里0少往哪里移，所以最优的分界点一定是0的中点，每次取0的中点就行
另一种做法是单调指针，我们发现当区间移动的时候，分界点的移动是单调的；为什么呢？引用Yubai的证明
如果你把左边一个0移到右边，左边优的会变多，右边优的变少，指针不降（右移）
把左边一个1移到右边，只有两头发生了变化，指针不降（不动）
所以满足单调，单调指针扫过去，均摊On
下面本该贴代码结束了，但是此时
玄学做法出现了！
直接将每段序列中点视为分界点，On解决，AC
看上去没有正确性，但是经过一夜对拍之后依然没有Hack掉
实际上，它是正确的
我们考虑最终结果一定是一段连续的01串，那么他可以把1均匀分到两边，这样答案就可以取序列中点。
事实上，通过枚举区间，一定可以使得中点在0的中点区间中出现，而非中点的其他点不一定在中点区间内出现，且离中点越远出现概率越小，即
序列中点一定可以得出正确答案
所以枚举中点正确，而且码量小
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=2000050;
char a[N];
int sumb[N],sufb[N],sum[N],suf[N],sumr[N],sufr[N];
inline void clear(int m)
{
for(int i=1;i<=2*m;i++)
sumb[i]=sufb[i]=sum[i]=suf[i]=sumr[i]=sufr[i]=0;
}
signed main()
{
int T;cin>>T;
while(T--)
{
scanf("%s",a+1);
int n=strlen(a+1);
for(int i=1;i<=n;i++)a[i+n]=a[i];
int ans=999999999999;
for(int i=1;i<=2*n;i++)
{
sumb[i]=sumb[i-1];sum[i]=sum[i-1];sumr[i]=sumr[i-1];
if(a[i]=='B')sumb[i]++;
if(a[i]=='R')sum[i]+=sumb[i-1],sumr[i]++;
}
for(int i=2*n;i>=1;i--)
{
sufb[i]=sufb[i+1];suf[i]=suf[i+1];sufr[i]=sufr[i+1];
if(a[i]=='B')sufb[i]++;
if(a[i]=='R')suf[i]+=sufb[i+1],sufr[i]++;
}
for(int i=1;i<=n;i++)
{
int p=i+n-1,j=(i+p)/2;
int qz=sum[j]-sum[i-1]-sumb[i-1]*(sumr[j]-sumr[i-1]),
hz=suf[j]-suf[p+1]-sufb[p+1]*(sufr[j]-sufr[p+1]);
ans=min(ans,qz+hz);
}
printf("%lld\n",ans);
clear(n);
}
}
我的常数大，因为我太菜了
这种东西觉得想明白了收获还是挺大的，真正追求的不只是那个绿勾，还有题背后的东西
执.
