决策树
注:此博文只是自己总结的笔记,参考很很多大牛的博客。
决策树算法之ID3算法
1.奥卡姆剃刀:
若有多个假设和观察值一致,则选择简单的那个。(be simple)
2.算法核心思想:
期望信息越小,信息增益越大,从而纯度越高。ID3算法以信息增益为度量选择,选择分裂后信息增益最大的属性进行分裂。所以,ID3的思想便是:
1)自顶向下的贪婪搜索遍历可能的决策树空间构造决策树(此方法是ID3算法和C4.5算法的基础);
2)从“哪一个属性将在树的根节点被测试”开始;
3)使用统计测试来确定每一个实例属性单独分类训练样例的能力,分类能力最好的属性作为树的根结点测试(如何定义或者评判一个属性是分类能力最好的呢?这便是下文将要介绍的信息增益,or 信息增益率)。
4)然后为根结点属性的每个可能值产生一个分支,并把训练样例排列到适当的分支(也就是说,样例的该属性值对应的分支)之下。
5)重复这个过程,用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。
以学习布尔函数的ID3算法为例:

3.寻找最佳分类属性
3.1熵:信息增益的度量标准,刻画了任意样例的纯度,即每条消息中包含的信息的平均量。信息论中对熵的一种解释是熵确定了要编码集合S中任意成员的分类所需要的最少二进制位数。
熵是根据当前属性的最终分类来计算的,对于而分类来说,假设p为正类在该分类下比例,则熵为-[plogp+(1-p)log(1-p)].
当取自有限的样本时,熵的公式可以表示为:
/**
* 计算数据按照不同方式划分的熵
* @param remainData剩余的数据
* @param attrName待划分的属性,在算信息增益的时候会使用到
* @param attrValue划分的子属性值
* @param isParent是否分子属性划分还是原来不变的划分
*/
private double computeEntropy(String[][] remainData, String attrName,
String value, boolean isParent) {
// 实例总数
int total = 0;
// 正实例数
int posNum = 0;
// 负实例数
int negNum = 0;
// 还是按列从左往右遍历属性
for (int j = 1; j < attrNames.length; j++) {
// 找到了指定的属性
if (attrName.equals(attrNames[j])) {
for (int i = 1; i < remainData.length; i++) {
// 如果是父结点直接计算熵或者是通过子属性划分计算熵,这时要进行属性值的过滤
if (isParent|| (!isParent && remainData[i][j].equals(value))) {
if (remainData[i][attrNames.length - 1].equals(YES)) {
// 判断此行数据是否为正实例
posNum++;
} else {
negNum++;
}
}
}
}
}
total = posNum + negNum;
double posProbobly = (double) posNum / total;
double negProbobly = (double) negNum / total;
if (posProbobly == 1 || posProbobly == 0) {
// 如果数据全为同种类型,则熵为0,否则带入下面的公式会报错
return 0;
}
double entropyValue = -posProbobly * Math.log(posProbobly)
/ Math.log(2.0) - negProbobly * Math.log(negProbobly)
/ Math.log(2.0);
// 返回计算所得熵
return entropyValue;
}
3.2 信息增益:熵作为衡量训练样例集合纯度的标准,现在可以定义属性分类训练数据的效力的度量标准。简单的说,一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低(或者说,样本按照某属性划分时造成熵减少的期望)。更精确地讲,一个属性A相对样例集合S的信息增益Gain(S,A)被定义为:
当对S的一个任意成员的目标值编码时,Gain(S,A)的值是在知道属性A的值后可以节省的二进制位数。
选择信息增益大的作为分类属性更佳。
/**
* 为某个属性计算信息增益
* @param remainData剩余的数据
* @param value待划分的属性名称
*/
private double computeGain(String[][] remainData, String value) {
double gainValue = 0;
double entropyOri = 0;// 源熵的大小将会与属性划分后进行比较
double childEntropySum = 0;// 子划分熵和
int childValueNum = 0;// 属性子类型的个数
ArrayList<String> attrTypes = attrValue.get(value);// 属性值的种数
HashMap<String, Integer> ratioValues = new HashMap<>();// 子属性对应的权重比
for (int i = 0; i < attrTypes.size(); i++) {
// 首先都统一计数为0
ratioValues.put(attrTypes.get(i), 0);
}
// 还是按照一列,从左往右遍历
for (int j = 1; j < attrNames.length; j++) {
// 判断是否到了划分的属性列
if (value.equals(attrNames[j])) {
for (int i = 1; i <= remainData.length - 1; i++) {
childValueNum = ratioValues.get(remainData[i][j]);
// 增加个数并且重新存入
childValueNum++;
ratioValues.put(remainData[i][j], childValueNum);
}
}
}
// 计算原熵的大小
entropyOri = computeEntropy(remainData, value, null, true);
for (int i = 0; i < attrTypes.size(); i++) {
double ratio = (double) ratioValues.get(attrTypes.get(i))
/ (remainData.length - 1);
childEntropySum += ratio
* computeEntropy(remainData, value, attrTypes.get(i), false);
}
// 二者熵相减就是信息增益
gainValue = entropyOri - childEntropySum;
return gainValue;
}
4.ID3算法无回溯,局部最优而非全局最优
决策树算法之C4.5
1.相比ID3算法的改进之处:
1)用信息增益率来选择属性,减少信息增益对可取值数目较多的属性的偏好。
2)在树的构造过程中进行剪枝。
3)能处理非离散数据。
4)能对不完整数据进行处理。
2.信息增益率:
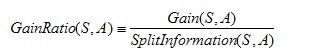
其中,分裂信息度量被定义为(分裂信息用来衡量属性分裂数据的广度和均匀):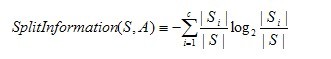
其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。注意分裂信息实际上就是S关于属性A的各值的熵。这与我们前面对熵的使用不同,在那里我们只考虑S关于学习到的树要预测的目标属性的值的熵。
需要注意的是,信息增益比对可取数目较少的属性有所偏好,因此,C4.5算法并不是直接选取信息增益比大的属性进行分类,而是使用了一个启发式:即先从候选属性中选择信息增益高于平均水平的属性,然后再在他们之中选择信息增益比最大的作为分类属性。
3.C4.5算法构造决策树的过程:
- Function C4.5(R:包含连续属性的无类别属性集合,C:类别属性,S:训练集)
- /返回一棵决策树/
- Begin
- If S为空,返回一个值为Failure的单个节点;
- If S是由相同类别属性值的记录组成,
- 返回一个带有该值的单个节点;
- If R为空,则返回一个单节点,其值为在S的记录中找出的频率最高的类别属性值;
- [注意未出现错误则意味着是不适合分类的记录];
- For 所有的属性R(Ri) Do
- If 属性Ri为连续属性,则
- Begin
- 将Ri的最小值赋给A1:
- 将Rm的最大值赋给Am;/m值手工设置/
- For j From 2 To m-1 Do Aj=A1+j*(A1Am)/m; /计算每个分割点Ri的信息增益
- 将Ri点的基于{< =Aj,>Aj}的最大信息增益属性(Ri,S)赋给A;
- End;
- 将R中属性之间具有最大信息增益的属性(D,S)赋给D;
- 将属性D的值赋给{dj/j=1,2...m};
- 将分别由对应于D的值为dj的记录组成的S的子集赋给{sj/j=1,2...m};
- 返回一棵树,其根标记为D;树枝标记为d1,d2...dm;
- 再分别构造以下树:
- C4.5(R-{D},C,S1),C4.5(R-{D},C,S2)...C4.5(R-{D},C,Sm);
- End C4.5
在写代码前,先看下思路:
此处给出Java实现ID3算法的代码:comes from :https://github.com/linyiqun/DataMiningAlgorithm
ID3Tool
package DataMing_ID3;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Map.Entry;
import java.util.Set;
/**
* ID3算法实现类
*
* @author lyq
*
*/
public class ID3Tool {
// 类标号的值类型
private final String YES = "Yes";
private final String NO = "No";
// 所有属性的类型总数,在这里就是data源数据的列数
private int attrNum;
private String filePath;
// 初始源数据,用一个二维字符数组存放模仿表格数据
private String[][] data;
// 数据的属性行的名字
private String[] attrNames;
// 每个属性的值所有类型
private HashMap<String, ArrayList<String>> attrValue;
public ID3Tool(String filePath) {
this.filePath = filePath;
attrValue = new HashMap<>();
}
/**
* 从文件中读取数据到data数组
*/
private void readDataFile() {
File file = new File(filePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
data = new String[dataArray.size()][];
dataArray.toArray(data);
attrNum = data[0].length;
attrNames = data[0];
/*
* for(int i=0; i<data.length;i++){ for(int j=0; j<data[0].length; j++){
* System.out.print(" " + data[i][j]); }
*
* System.out.print("\n"); }
*/
}
/**
* 首先初始化每种属性的值的所有类型,用于后面的子类熵的计算时用
*/
private void initAttrValue() {
ArrayList<String> tempValues;
// 按照列的方式,从左往右找
for (int j = 1; j < attrNum; j++) {
// 从一列中的上往下开始寻找值
tempValues = new ArrayList<>();
for (int i = 1; i < data.length; i++) {
if (!tempValues.contains(data[i][j])) {
// 如果这个属性的值没有添加过,则添加
tempValues.add(data[i][j]);
}
}
// 一列属性的值已经遍历完毕,复制到map属性表中
attrValue.put(data[0][j], tempValues);
}
/*
* for(Map.Entry entry : attrValue.entrySet()){
* System.out.println("key:value " + entry.getKey() + ":" +
* entry.getValue()); }
*/
}
/**
* 计算数据按照不同方式划分的熵
*
* @param remainData
* 剩余的数据
* @param attrName
* 待划分的属性,在算信息增益的时候会使用到
* @param attrValue
* 划分的子属性值
* @param isParent
* 是否分子属性划分还是原来不变的划分
*/
private double computeEntropy(String[][] remainData, String attrName,
String value, boolean isParent) {
// 实例总数
int total = 0;
// 正实例数
int posNum = 0;
// 负实例数
int negNum = 0;
// 还是按列从左往右遍历属性
for (int j = 1; j < attrNames.length; j++) {
// 找到了指定的属性
if (attrName.equals(attrNames[j])) {
for (int i = 1; i < remainData.length; i++) {
// 如果是父结点直接计算熵或者是通过子属性划分计算熵,这时要进行属性值的过滤
if (isParent
|| (!isParent && remainData[i][j].equals(value))) {
if (remainData[i][attrNames.length - 1].equals(YES)) {
// 判断此行数据是否为正实例
posNum++;
} else {
negNum++;
}
}
}
}
}
total = posNum + negNum;
double posProbobly = (double) posNum / total;
double negProbobly = (double) negNum / total;
if (posProbobly == 1 || posProbobly == 0) {
// 如果数据全为同种类型,则熵为0,否则带入下面的公式会报错
return 0;
}
double entropyValue = -posProbobly * Math.log(posProbobly)
/ Math.log(2.0) - negProbobly * Math.log(negProbobly)
/ Math.log(2.0);
// 返回计算所得熵
return entropyValue;
}
/**
* 为某个属性计算信息增益
*
* @param remainData
* 剩余的数据
* @param value
* 待划分的属性名称
* @return
*/
private double computeGain(String[][] remainData, String value) {
double gainValue = 0;
// 源熵的大小将会与属性划分后进行比较
double entropyOri = 0;
// 子划分熵和
double childEntropySum = 0;
// 属性子类型的个数
int childValueNum = 0;
// 属性值的种数
ArrayList<String> attrTypes = attrValue.get(value);
// 子属性对应的权重比
HashMap<String, Integer> ratioValues = new HashMap<>();
for (int i = 0; i < attrTypes.size(); i++) {
// 首先都统一计数为0
ratioValues.put(attrTypes.get(i), 0);
}
// 还是按照一列,从左往右遍历
for (int j = 1; j < attrNames.length; j++) {
// 判断是否到了划分的属性列
if (value.equals(attrNames[j])) {
for (int i = 1; i <= remainData.length - 1; i++) {
childValueNum = ratioValues.get(remainData[i][j]);
// 增加个数并且重新存入
childValueNum++;
ratioValues.put(remainData[i][j], childValueNum);
}
}
}
// 计算原熵的大小
entropyOri = computeEntropy(remainData, value, null, true);
for (int i = 0; i < attrTypes.size(); i++) {
double ratio = (double) ratioValues.get(attrTypes.get(i))
/ (remainData.length - 1);
childEntropySum += ratio
* computeEntropy(remainData, value, attrTypes.get(i), false);
// System.out.println("ratio:value: " + ratio + " " +
// computeEntropy(remainData, value,
// attrTypes.get(i), false));
}
// 二者熵相减就是信息增益
gainValue = entropyOri - childEntropySum;
return gainValue;
}
/**
* 计算信息增益比
*
* @param remainData
* 剩余数据
* @param value
* 待划分属性
* @return
*/
private double computeGainRatio(String[][] remainData, String value) {
double gain = 0;
double spiltInfo = 0;
int childValueNum = 0;
// 属性值的种数
ArrayList<String> attrTypes = attrValue.get(value);
// 子属性对应的权重比
HashMap<String, Integer> ratioValues = new HashMap<>();
for (int i = 0; i < attrTypes.size(); i++) {
// 首先都统一计数为0
ratioValues.put(attrTypes.get(i), 0);
}
// 还是按照一列,从左往右遍历
for (int j = 1; j < attrNames.length; j++) {
// 判断是否到了划分的属性列
if (value.equals(attrNames[j])) {
for (int i = 1; i <= remainData.length - 1; i++) {
childValueNum = ratioValues.get(remainData[i][j]);
// 增加个数并且重新存入
childValueNum++;
ratioValues.put(remainData[i][j], childValueNum);
}
}
}
// 计算信息增益
gain = computeGain(remainData, value);
// 计算分裂信息,分裂信息度量被定义为(分裂信息用来衡量属性分裂数据的广度和均匀):
for (int i = 0; i < attrTypes.size(); i++) {
double ratio = (double) ratioValues.get(attrTypes.get(i))
/ (remainData.length - 1);
spiltInfo += -ratio * Math.log(ratio) / Math.log(2.0);
}
// 计算机信息增益率
return gain / spiltInfo;
}
/**
* 利用源数据递归构造决策树
*/
private void buildDecisionTree(AttrNode node, String parentAttrValue, String[][] remainData, ArrayList<String> remainAttr, boolean isID3) {
node.setParentAttrValue(parentAttrValue);
String attrName = "";
double gainValue = 0;
double tempValue = 0;
// 如果只有1个属性则直接返回
if (remainAttr.size() == 1) {
System.out.println("attr null");
return;
}
// 选择剩余属性中信息增益最大的作为下一个分类的属性
for (int i = 0; i < remainAttr.size(); i++) {
// 判断是否用ID3算法还是C4.5算法
if (isID3) {
// ID3算法采用的是按照信息增益的值来比
tempValue = computeGain(remainData, remainAttr.get(i));
} else {
// C4.5算法进行了改进,用的是信息增益率来比,克服了用信息增益选择属性时偏向选择取值多的属性的不足
tempValue = computeGainRatio(remainData, remainAttr.get(i));
}
//选择信息增益最大的属性,并保存属性名为attrName
if (tempValue > gainValue) {
gainValue = tempValue;
attrName = remainAttr.get(i);
}
}
//设置该节点的分类属性
node.setAttrName(attrName);
//获得该分类属性的所有属性值
ArrayList<String> valueTypes = attrValue.get(attrName);
//从剩余属性集中删除已选属性
remainAttr.remove(attrName);
//为每一个属性类创建一个节点
AttrNode[] childNode = new AttrNode[valueTypes.size()];
String[][] rData;
for (int i = 0; i < valueTypes.size(); i++) {
// 移除非此值类型的数据
rData = removeData(remainData, attrName, valueTypes.get(i));
childNode[i] = new AttrNode();
boolean sameClass = true;
ArrayList<String> indexArray = new ArrayList<>();
for (int k = 1; k < rData.length; k++) {
indexArray.add(rData[k][0]);
// 判断是否为同一类的
if (!rData[k][attrNames.length - 1]
.equals(rData[1][attrNames.length - 1])) {
// 只要有1个不相等,就不是同类型的
sameClass = false;
break;
}
}
if (!sameClass) {
// 创建新的对象属性,对象的同个引用会出错
ArrayList<String> rAttr = new ArrayList<>();
for (String str : remainAttr) {
rAttr.add(str);
}
buildDecisionTree(childNode[i], valueTypes.get(i), rData,
rAttr, isID3);
} else {
// 如果是同种类型,则直接为数据节点
childNode[i].setParentAttrValue(valueTypes.get(i));
childNode[i].setChildDataIndex(indexArray);
}
}
node.setChildAttrNode(childNode);
}
/**
* 属性划分完毕,进行数据的移除
*
* @param srcData
* 源数据
* @param attrName
* 划分的属性名称
* @param valueType
* 属性的值类型
*/
private String[][] removeData(String[][] srcData, String attrName,String valueType) {
String[][] desDataArray;
ArrayList<String[]> desData = new ArrayList<>();
ArrayList<String[]> selectData = new ArrayList<>();
selectData.add(attrNames);
// 数组数据转化到列表中,方便移除
for (int i = 0; i < srcData.length; i++) {
desData.add(srcData[i]);
}
// 还是从左往右一列列的查找
for (int j = 1; j < attrNames.length; j++) {
if (attrNames[j].equals(attrName)) {
for (int i = 1; i < desData.size(); i++) {
if (desData.get(i)[j].equals(valueType)) {
// 如果匹配这个数据,则移除其他的数据
selectData.add(desData.get(i));
}
}
}
}
desDataArray = new String[selectData.size()][];
selectData.toArray(desDataArray);
return desDataArray;
}
/**
* 开始构建决策树
*
* @param isID3
* 是否采用ID3算法构架决策树
*/
public void startBuildingTree(boolean isID3) {
readDataFile();
initAttrValue();
ArrayList<String> remainAttr = new ArrayList<>();
// 添加属性,除了最后一个类标号属性
for (int i = 1; i < attrNames.length - 1; i++) {
remainAttr.add(attrNames[i]);
}
AttrNode rootNode = new AttrNode();
buildDecisionTree(rootNode, "", data, remainAttr, isID3);
showDecisionTree(rootNode, 1);
}
/**
* 显示决策树
*
* @param node
* 待显示的节点
* @param blankNum
* 行空格符,用于显示树型结构
*/
private void showDecisionTree(AttrNode node, int blankNum) {
System.out.println();
for (int i = 0; i < blankNum; i++) {
System.out.print("\t");
}
System.out.print("--");
// 显示分类的属性值
if (node.getParentAttrValue() != null
&& node.getParentAttrValue().length() > 0) {
System.out.print(node.getParentAttrValue());
} else {
System.out.print("--");
}
System.out.print("--");
if (node.getChildDataIndex() != null
&& node.getChildDataIndex().size() > 0) {
String i = node.getChildDataIndex().get(0);
System.out.print("类别:"
+ data[Integer.parseInt(i)][attrNames.length - 1]);
System.out.print("[");
for (String index : node.getChildDataIndex()) {
System.out.print(index + ", ");
}
System.out.print("]");
} else {
// 递归显示子节点
System.out.print("【" + node.getAttrName() + "】");
for (AttrNode childNode : node.getChildAttrNode()) {
showDecisionTree(childNode, 2 * blankNum);
}
}
}
}
AttrNode
package DataMing_ID3;
import java.util.ArrayList;
/**
* 属性节点,不是叶子节点
* @author lyq
*
*/
public class AttrNode {
//当前属性的名字
private String attrName;
//父节点的分类属性值
private String parentAttrValue;
//属性子节点
private AttrNode[] childAttrNode;
//孩子叶子节点
private ArrayList<String> childDataIndex;
public String getAttrName() {
return attrName;
}
public void setAttrName(String attrName) {
this.attrName = attrName;
}
public AttrNode[] getChildAttrNode() {
return childAttrNode;
}
public void setChildAttrNode(AttrNode[] childAttrNode) {
this.childAttrNode = childAttrNode;
}
public String getParentAttrValue() {
return parentAttrValue;
}
public void setParentAttrValue(String parentAttrValue) {
this.parentAttrValue = parentAttrValue;
}
public ArrayList<String> getChildDataIndex() {
return childDataIndex;
}
public void setChildDataIndex(ArrayList<String> childDataIndex) {
this.childDataIndex = childDataIndex;
}
}
DataNode
package DataMing_ID3;
/**
* 存放数据的叶子节点
* @author lyq
*
*/
public class DataNode {
/**
* 数据的标号
*/
private int dataIndex;
public DataNode(int dataIndex){
this.dataIndex = dataIndex;
}
}
测试数据:
Day OutLook Temperature Humidity Wind PlayTennis
1 Sunny Hot High Weak No
2 Sunny Hot High Strong No
3 Overcast Hot High Weak Yes
4 Rainy Mild High Weak Yes
5 Rainy Cool Normal Weak Yes
6 Rainy Cool Normal Strong No
7 Overcast Cool Normal Strong Yes
8 Sunny Mild High Weak No
9 Sunny Cool Normal Weak Yes
10 Rainy Mild Normal Weak Yes
11 Sunny Mild Normal Strong Yes
12 Overcast Mild High Strong Yes
13 Overcast Hot Normal Weak Yes
14 Rainy Mild High Strong No




