梯度下降&随机梯度下降&批梯度下降
梯度下降法
下面的h(x)是要拟合的函数,J(θ)损失函数,theta是参数,要迭代求解的值,theta求解出来了那最终要拟合的函数h(θ)就出来了。其中m是训练集的记录条数,j是参数的个数。
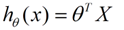

梯度下降法流程:
(1)先对θ随机赋值,可以是一个全零的向量。
(2)改变θ的值,使J(θ)按梯度下降的方向减少。
以上式为例:
(1)对于我们的函数J(θ)求关于θ的偏导:
(2)下面是更新的过程,也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值,-后面的部分表示按梯度方向减少的量,α表示步长,也就是每次按照梯度减少的方向变化多少。
值得注意的是,梯度是有方向的,对于一个向量θ,每一维分量θi都可以求出一个梯度的方向,我们就可以找到一个整体的方向,在变化的时候,我们就朝着下降最多的方向进行变化就可以达到一个最小点,不管它是局部的还是全局的。
批量梯度下降
(1)将J(θ)对θ求偏导,得到每个θ对应的梯度(m为训练样本的个数):
(2)由于是要最小化风险函数,所以按每个参数theta的梯度负方向,来更新每个theta
(3)从上面公式可以注意到,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果m很大,那么可想而知这种方法的迭代速度!!所以,这就引入了另外一种方法,随机梯度下降。
随机梯度下降
(1)上面的风险函数可以写成如下这种形式,损失函数对应的是训练集中每个样本的粒度,而上面批量梯度下降对应的是所有的训练样本:
(2)每个样本的损失函数,对theta求偏导得到对应梯度,来更新theta
(3)随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。




