半监督学习(四)——基于图的半监督学习
基于图的半监督学习
以一个无标签数据的例子作为垫脚石
Alice正在翻阅一本《Sky and Earth》的杂志,里面是关于天文学和旅行的文章。Alice不会英文,她只能通过文章中的图片来猜测文章的类别。比如第一个故事是“Bridge Asteroid”有一张多坑的小行星图片,那么它很明显是天文学类别的。第二个故事是“Yellowstone Camping”有张灰熊的图片,那么将它分类到旅行类别。但是其它文章没有图片,Alice不能给它们分类。Alice是一个聪明的人,她注意到其他文章的标题“Asteroid and Comet,” “Comet Light Curve,” “Camping in Denali,” and “Denali Airport.”她猜测如果两个文章的标题中有相同的单词,它们可能是一个类的,然后他就画出这样一幅图:
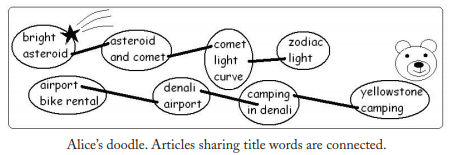
这其实就是基于图的半监督学习的一个例子。
图的概念
我们首先来看看如何从训练数据中构建出图,给定半监督数据集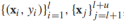 ,每个数据样本(有标签&无标签)是图上的一个顶点,显然,图会非常大,因为无标签数据很多,一旦图构建完成,学习的过程就包括给图中的每一个定点设置标签y值。在图中可以通过边将有标签和无标签数据点相连,边通常是无向的,表示的是两个节点(样本)之间的相似性。将边权重记作wij,wij越大,xi和xj越相似,两者的标签越可能相同。所以边权重非常重要,人们常常将边的权值定义为如下形式:
,每个数据样本(有标签&无标签)是图上的一个顶点,显然,图会非常大,因为无标签数据很多,一旦图构建完成,学习的过程就包括给图中的每一个定点设置标签y值。在图中可以通过边将有标签和无标签数据点相连,边通常是无向的,表示的是两个节点(样本)之间的相似性。将边权重记作wij,wij越大,xi和xj越相似,两者的标签越可能相同。所以边权重非常重要,人们常常将边的权值定义为如下形式:
- 全连接图:
每一对定点之间都有边相连,边的权重随欧式距离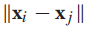 的增加而降低,常用的权重方程如下:
的增加而降低,常用的权重方程如下: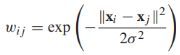 ,σ叫做带宽参数用来控制权重衰减的速度。这个权重方程和高斯方程的形式相同,也叫做高斯核或者径向基函数;
,σ叫做带宽参数用来控制权重衰减的速度。这个权重方程和高斯方程的形式相同,也叫做高斯核或者径向基函数;
- KNN图:
每一个定点定义它的欧式距离上的最近邻,注意,如果xi在xj的k近邻内,xj不一定在xi的k近邻内,如果xi,xj中有一个在对方的k近邻内我们就用边将它们连接,这就意味着一个定点可能会有超过k条边,如果xi,xj有边相连,边的权重wij就是1,否则为0。KNN图可以自适应地适应样本在特征空间的密度(密集区KNN范围的半径小);
- εNN图:
将距离小于ε的顶点连一条边。
当然,这些都是很一般的方法,如果有问题相关领域知识,可以构建更好的图,可以定义更好的距离方程,连接性以及边权值。
接下来,我们介绍一些基于图的半监督学习算法,它们在损失函数和正则化的选择上不同,为了简单起见,我们假设标签为{-1,1}。
MINCUT
我们将带有正标签的样本作为源点(就好像流从这里出发流经边),相似的,负标签样本作为终点(流消失的点),目标是找到一个最小的边集,使得删除这些边可以阻止所有从源点到终点的流,我们定义这样的一组边集叫做“cut”,割的大小用这些边的权重和来定义。一旦图被“割”开,与源点相连的点都被标记为正,反之为负。也就是说,我们想要找到这样的一个作用在顶点上的函数f(x){-1,1}用来标记x的标签,使得对于有标签样本来说f(xi)=yi,而且cut最小: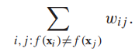
我们将最小割问题形式化为正则化风险最小化问题(合适的损失函数和正则化器)。对任何有标签的顶点xi,f(xi)就是给定的标签yi,可以用这样一个损失函数来表示: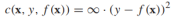 ,而正则化项则对应cut的大小,考虑到所有无标签样本的类别非负即正,cut的大小可以重写为
,而正则化项则对应cut的大小,考虑到所有无标签样本的类别非负即正,cut的大小可以重写为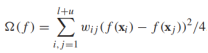 。注意,当前的和是针对所有点对的,如果xi,xj不相连,wij=0。那么最小割的正则化风险最小化问题可以写作
。注意,当前的和是针对所有点对的,如果xi,xj不相连,wij=0。那么最小割的正则化风险最小化问题可以写作

这是一个整数规划问题,因此,最小割问题可以有许多多项式时间算法可以解决。
这种形式的最小割问题可能存在多个最优解,比如下图有两个带标签点一正一负,每条边有相同的权重,有6种最小割解决方案(移除任意一条边即可)

HARMONIC FUNCTION
第二种基于图的半监督学习算法是调和函数,对于有标签数据,调和函数的值为标签值,对于无标签数据,标签值是权重平均:
也就是说,无标签顶点的值就是其邻居顶点标签值的权重平均,然后把它代入上面提到过的目标函数,并松弛f使它的值域为实数:
相当于求解: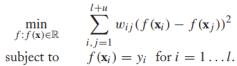
对f进行松弛使得f有一个闭式解,也就是说上述目标方程有全局最优解,缺点是f(x)现在是一个[-1,1]的实数,并不能直接作为一个标签。这可以通过设定阈值进行处理(如,如果f(x)>=0,预测标签y=1,否则为-1).
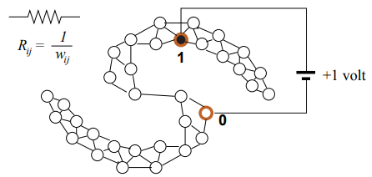
调和函数有许多有趣的解释,比如,将图看作一张电网,每一条边的电阻为1/wij,有标签的点连接到1v的电池,正标签顶点连接电池正极,负标签顶点连接电池负极,每个节点两端的电压就是调和函数值,如下图所示:
调和函数也可以解释为图上的随机游走,想象一个粒子在顶点i上,那么这个粒子会随机走到下一个顶点j的概率是![]() ,随机游走以这种方式继续,直到粒子到达一个有标记的顶点。那么顶点i的调和函数值f(xi)就是粒子从i顶点出发最终走到一个正标签的顶点的概率,如下图所示:
,随机游走以这种方式继续,直到粒子到达一个有标记的顶点。那么顶点i的调和函数值f(xi)就是粒子从i顶点出发最终走到一个正标签的顶点的概率,如下图所示: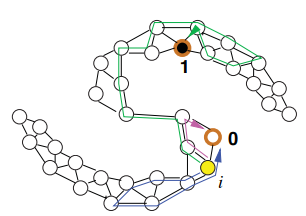
求解调和函数的过程是迭代的,初始的,我们设定:对于有标签顶点,f(xi)=yi,对于无标签顶点,f为任意值。每一轮迭代都用无标签顶点邻居的权重平均更新该无标签顶点的标签值: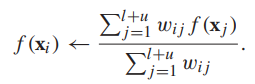
可以看出,无论初始值是多少,该迭代过程可以保证调和函数值收敛。这个过程也被称为标签传播。
最后,我们来讨论调和函数的闭式解:令W是一个(l+u)*(l+u)的权重矩阵,其中的元素是权重值wij。由于图是无向的,所以W是一个对称矩阵。它的元素是非负的, 是顶点i的加权度(与i相连的所有边的和)。令D是(l+u)*(l+u)的对角矩阵,对角元素是Dii,定义非标准化的图拉普拉斯矩阵L=D-W。
是顶点i的加权度(与i相连的所有边的和)。令D是(l+u)*(l+u)的对角矩阵,对角元素是Dii,定义非标准化的图拉普拉斯矩阵L=D-W。
令 是所有顶点f值的向量,那么正则化项可以写作:
是所有顶点f值的向量,那么正则化项可以写作: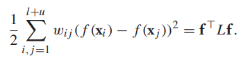
流形正则化
上面说的Mincut和harmonic function 都是转换式的学习方法,它们无法直接一个之前没有出现过的样本的标签,除非把该新样本加入图中成为新的节点,然后重新计算。如果我们要预测大量的数据,这显然是不现实的,所以我们需要的是一种归纳的半监督学习算法。而且,Mincut和harmonic function都规定有标签数据的f(x)=y,在真实数据集中,可能存在标签错误点或是噪声点,我们希望f可以偶尔与给定标签不同。
流形正则可以解决这两个问题。这是一种归纳学习算法,它在整个特征空间上定义f: ,通过图拉普拉斯变换,f被正则为对图平滑。然而这个正则器只能控制f的值在(l+u)训练集上的大小,为了防止f在训练集以外的样本上变化不平滑(泛化能力较差),有必要加第二个正则项,所以,流形正则的正则项可以写作:
,通过图拉普拉斯变换,f被正则为对图平滑。然而这个正则器只能控制f的值在(l+u)训练集上的大小,为了防止f在训练集以外的样本上变化不平滑(泛化能力较差),有必要加第二个正则项,所以,流形正则的正则项可以写作:![]()
那么完整的流形正则目标函数可以写作(损失函数可以根据实际情况进行替换):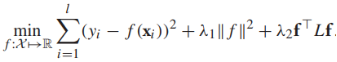
已经有有效的算法找到最优的f。除了非标准化的图拉普拉斯矩阵L之外,也常常使用标准化的图拉普拉斯矩阵:
![]()
这使得正则项有一些不同
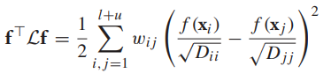
The Assumption of graph-based method
基于图的半监督学习假设:图的标签是“平滑”的,标签在图上的变化非常缓慢,也就是说如果两个样本在图上有强边相连,它们的标签很大概率相同。平滑的概念可以用谱图理论来精确表示。向量φ是方阵A的一个特征向量如果Aφ=λφ(λ是特征向量对应的特征值)。如果φ是一个特征向量,cφ(c!=0)也是一个特征向量。但是我们关注单位特征向量||φ||=1,普图理论涉及一个图的特征向量和特征值,用拉普拉斯矩阵L来表示。我们将分析非正则化拉普拉斯矩阵L,它有如下特性:
- L有(l+u)个特征值(可重复)和对应的特征向量
 ,这些对叫做图谱,特征向量是正交的
,这些对叫做图谱,特征向量是正交的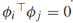 (i!=j)。
(i!=j)。 - 拉普拉斯矩阵可分解为外积的加权和:
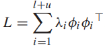
- 特征值是非负实数,
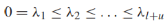
- 图有k个连通分量当且仅当
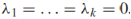 对应的特征向量在单个连通分量上是常数或0。
对应的特征向量在单个连通分量上是常数或0。
小结:
本章主要介绍了使用图的相关知识解决半监督学习的问题。我们讨论的几种算法都基于预测的标签在图上是平滑的,并介绍了一些关于谱图理论的概念来证明这些方法。在之后的文章中,我们将讨论半监督支持向量机。
希望大家多多支持我的公众号,扫码关注,我们一起学习,一起进步~




