Codeforces Round 884 (Div. 1 + Div. 2)
A. Subtraction Game
答案就是a+b此时后手必胜因为无论怎么操作后手都可保证自己取的时候一次全部取完
#include <bits/stdc++.h>
using namespace std;
void solve(){
int a , b;
cin >> a >> b;
cout << a + b << "\n";
return ;
}
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int t;
cin >> t;
while( t -- )
solve();
return 0;
}
B. Permutations & Primes
赛时没有仔细想而是打了个表找规律,结果找到假规律了。
构造的方法是把2,3放在首尾,把 1 放在尽可能中间的地方,其他随意放即可。
这样包含 1 且不包含 2 或 3 的区间数量最多
#include <bits/stdc++.h>
using namespace std;
bool prime( int x ){
if( x == 1 || x == 0 ) return false;
for( int i = 2 ; i * i <= x ; i ++ )
if( x % i == 0 ) return false;
return true;
}
void solve(){
int n;
cin >> n;
if( n == 1 )
cout << "1\n";
else if( n == 2 )
cout << "1 2\n";
else{
cout << "2 ";
int t = 4 , d = ( n - 3 ) / 2 ;
for( ; d ; d -- ,t ++ )
cout << t << " ";
cout << "1 ";
for( ; t <= n ; t ++ )
cout << t << " ";
cout <<"3\n";
}
}
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int t;
cin >> t;
while( t -- )
solve();
return 0;
}
C. Particles
可以发现奇数位的只能和奇数位的合并,同理偶数位的也只能和偶数位的合并。所以分奇偶来看,先来考虑奇数位置上的a,b,c,d,e先删掉c得到a,b+d,e,再删b+d得到a+e所以显然我们可以选择奇数位上任意几个数字求和。所以答案就变成了奇数位上的正数之和。偶数位同理,二者取较大值即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
void solve(){
int n , res;
cin >> n;
vector<int> a(n);
for( auto & i : a ) cin >> i;
res = *max_element(a.begin(), a.end());
if( res <= 0 ){
cout << res << "\n";
return ;
}
int cnt = 0;
for( int i = 0; i < n ; i += 2 ){
if( a[i] > 0 ) cnt += a[i];
}
res = max( res , cnt );
cnt = 0;
for( int i = 1; i < n ; i += 2 ){
if( a[i] > 0 ) cnt += a[i];
}
res = max( res , cnt );
cout << res << "\n";
return;
}
int32_t main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int t;
cin >> t;
while( t -- )
solve();
return 0;
}
D. Row Major
对于n我们求出所有的因子,然后计算因子的mex,间隔mex位的一定不会相邻,所以可以放相同的字母。
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n , t ;
cin >> n;
set<int> a;
for( int i = 1 ; i*i <= n ; i ++ ){
if( n % i ) continue;
a.insert(i);
if( i * i != n ) a.insert( n / i );
}
for( int i = 1 ; i ; i ++ )
if( a.count(i) == 0 ){
t = i;
break;
}
vector<int> b(n+1);
for( int i = 1 , p = 0 ; i <= t ; i ++ , p ++)
for( int j = i ; j <= n ; j += t )
b[j] = p;
for( int i = 1 ; i <= n ; i ++ )
cout << (char)(b[i] + 'a' );
cout << "\n";
}
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int t;
cin >> t;
while( t -- )
solve();
return 0;
}
E. Great Grids
首先我们把\(A,B,C\)离散化为\(0,1,2\)
这样的话,我们可以推出对于任意的一个\(2\times 2\)的格子满足一下性质
\[a_{1,2} - a_{1,1} = a_{2,2} - a_{2,1}(\mod3)\\
a_{2,1}-a_{1,1} = a_{2,2}-a_{1,2}(\mod3)
\]
根据这个性质,可以知道任意选择相邻两列作差相同,行有相同的结论。并且这个差值的取值只能为\(1,2\)

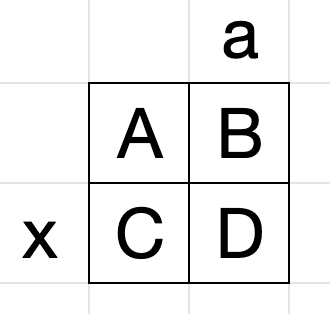
以上图为例,\(a,b\)表示列变换量,\(x,y\)表示行变换量,则有
\[B = (A+a)\mod 3 ,E = (D+a)\mod 3 , H = (G+a)\mod 3\\
D = (A+x)\mod 3 , E = (B+x) \mod3,F=(C+x)\mod 3
\]
有因为行变换量和列变换量的取值只有两种,所以可以知道变换量之间的关系只有相等和不相等两种。
再来看题目给出的额外限制,则可以推出
如果\(A=D\),则有\(a \ne x\)
如果\(B=C\),则有\(a=x\)
所以这题就是用扩展域并查集维护\(k\)个额外限制即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
map<int, int> cnt;
class dsu {
private:
vector<int> fa;
public:
dsu(int n = 1) {
fa = vector<int>(n + 1, -1), fa[0] = 0;
}
int getfa(int x) {
if (fa[x] < 0) return x;
return fa[x] = getfa(fa[x]);
}
void merge(int x, int y) {
x = getfa(x), y = getfa(y);
if (x == y) return;
if (fa[x] > fa[y]) swap(x, y);
fa[x] += fa[y], fa[y] = x;
}
bool same(int x, int y) {
x = getfa(x), y = getfa(y);
return (x == y);
}
};
void solve() {
int n, m, k, p, f = 1;
cin >> n >> m >> k, p = n + m;
dsu d(p * 2);
for (int xa, xb, ya, yb, x, y; k; k--) {
cin >> xa >> ya >> xb >> yb;
if (f == 0) continue;
x = xb, y = max(ya, yb) + n;
if (ya < yb) {
if (d.same(x, y)) f = 0;
else d.merge(x, y + p), d.merge(x + p, y);
} else {
if (d.same(x, y + p)) f = 0;
else d.merge(x, y), d.merge(x + p, y + p);
}
}
if( f ) cout << "YES\n";
else cout << "NO\n";
return;
}
int32_t main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int t;
cin >> t;
while (t--)
solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号