AtCoder Beginner Contest 303
A - Similar String
#include <bits/stdc++.h>
using namespace std;
#define int long long
int32_t main() {
int n;
string s , t;
cin >> n >> s >> t;
for( int i = 0 ; i < n ; i ++ ){
if( s[i] == t[i] ) continue;
if( s[i] == '1' && t[i] == 'l' ) continue;
if( s[i] == 'l' && t[i] == '1' ) continue;
if( s[i] == '0' && t[i] == 'o' ) continue;
if( s[i] == 'o' && t[i] == '0' ) continue;
cout << "No\n";
return 0;
}
cout << "Yes\n";
return 0;
}
B - Discord
#include <bits/stdc++.h>
using namespace std;
#define int long long
int32_t main() {
int n , m;
cin >> n >> m;
vector<vector<int>> a( n+1 , vector<int>(n+1 , 0 ));
for( ; m ; m -- ){
for( int u = -1 , v , i = 1 ; i <= n ; i ++ ){
cin >> v;
if( u == -1 ) u = v;
else a[u][v] = a[v][u] = 1 , u = v;
}
}
int res = 0;
for( int i = 1 ; i <= n ; i ++ )
for( int j = i + 1 ; j <=n ;j ++ ){
if( a[i][j] == 1 ) continue;
res ++;
}
cout << res;
return 0;
}
C - Dash
模拟就好了,注意每个点的补给只能用一次
#include <bits/stdc++.h>
using namespace std;
#define int long long
int32_t main() {
int n , m , h , k;
cin >> n >> m >> h >> k;
string s;
cin >> s;
set<pair<int,int>> rec;
for( int x , y ; m ; m -- )
cin >> x >> y , rec.emplace( x , y );
int r = 0 , c = 0;
for( auto i : s ){
if( h == 0 ){
cout << "No\n";
return 0;
}
if( i == 'R' ) r ++;
else if( i == 'L' ) r --;
else if( i == 'U' ) c ++;
else c --;
h --;
if( h < k && rec.count(make_pair(r,c)) ) h = k , rec.erase(make_pair(r,c));
}
cout << "Yes\n";
return 0;
}
D - Shift vs. CapsLock
\(f[i][0]\)表示前\(i\)位,且当前CapsLock没按下时的最小花费,\(f[i][1]\)表示前\(i\)位,且当前CapsLock按下时的最小花费。
然后模拟转移的过程即可。
#include <bits/stdc++.h>
using namespace std;
#define int long long
int32_t main() {
int x, y, z, n;
string s;
cin >> x >> y >> z >> s;
n = s.size();
vector<array<int, 2>> f(n + 1, array{(int) 1e18, (int) 1e18});
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
if (s[i - 1] == 'a') {
f[i][0] = min({f[i-1][0] + x, f[i - 1][1] + y + z, f[i - 1][1] + z + x});
f[i][1] = min({f[i-1][1] + y, f[i - 1][0] + x + z, f[i - 1][0] + z + y});
} else {
f[i][0] = min({f[i - 1][0] + y, f[i - 1][1] + x + z, f[i - 1][1] + z + y});
f[i][1] = min({f[i - 1][1] + x, f[i - 1][0] + y + z, f[i - 1][0] + z + x});
}
}
cout << min( f[n][0] , f[n][1] );
return 0;
}
E - A Gift From the Stars
我们把星星的中间的点叫做 root 点,我们的任务就是找到所有的 root 点,并且要输出 root 点的度数。
首先我们把最终的树拿出来,所有的叶子点走一步就一定是 root 点 ,而 root 点链接的所有的点都是星星的叶子点,如果星星的叶子点的度数不为 1,就说明了这个星星的叶子点和其他的星星的叶子点相连。
这样的话我们通过一个类似求拓扑序的方式就可以找到所有的 root 点了。
#include <bits/stdc++.h>
using namespace std;
#define int long long
int32_t main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
vector<vector<int>> e(n + 1);
vector<int> d(n + 1);
for (int i = n - 1, u, v; i; i--)
cin >> u >> v, e[u].push_back(v), e[v].push_back(u), d[u]++, d[v]++;
queue<int> q;
vector<bool> vis(n + 1, 0);
vector<int> res;
for( int i = 1 ; i <= n ; i ++ )
if( d[i] == 1 ) q.push(i);
while( !q.empty() ){
int u = q.front(); q.pop();
if( vis[u] ) continue;
vis[u] = 1;
int root;
for( auto i : e[u] ){
if( vis[i] ) continue;
root = i;
break;
}
res.push_back( e[root].size() );
vis[root] = 1;
for( auto i : e[root] ){
d[i] --;
vis[i] = 1;
if( d[i] == 1 ) {
for( auto j : e[i] ){
if(vis[j]) continue;
q.push(j);
break;
}
}
}
}
sort( res.begin() , res.end() );
for( auto i : res )
cout << i << " ";
return 0;
}
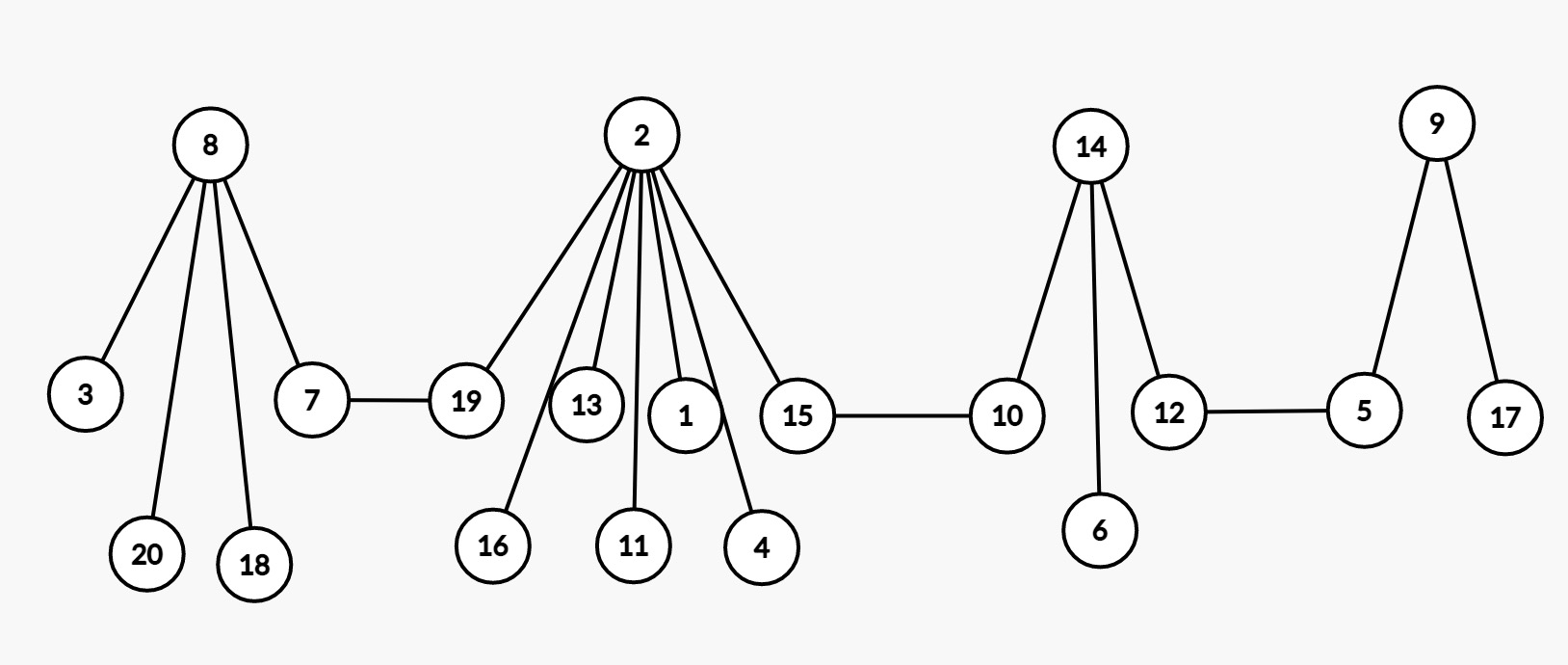
然后我们发现所有的图其实都是这种样子的。所以从选择任何一个叶子点作为跟求一遍深度,所有深度为\(2,5,8,11,14,17\dots\)的点都一定是 root 点。
#include <bits/stdc++.h>
using namespace std;
#define int long long
vector<vector<int>> e;
vector<int> dep;
void dfs(int x) {
for (auto i: e[x]) {
if (dep[i]) continue;
dep[i] = dep[x] + 1, dfs(i);
}
return;
}
int32_t main() {
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
int n;
cin >> n;
e = vector<vector<int>>(n + 1);
dep = vector<int>(n + 1, 0);
for (int i = n - 1, u, v; i; i--)
cin >> u >> v, e[u].push_back(v), e[v].push_back(u);
for (int i = 1; i <= n; i++) {
if (e[i].size() != 1) continue;
dep[i] = 1, dfs(i);
}
vector<int> res;
for( int i = 1 ; i <= n ; i ++ ){
if( (dep[i] - 2) % 3 ) continue;
res.push_back( e[i].size() );
}
sort(res.begin(), res.end());
for (auto i: res)
cout << i << " ";
return 0;
}
F - Damage over Time
首先这道题的难点在于攻击的持续时间无法确定。所以我们考虑二分的方式来枚举攻击的时间。
我们将技能按照\(t_i\)升序排列。如果剩余时间\(t\ge t_i\)那么技能\(i\)造成的伤害就是\(t_i\times d_i\),反之伤害就是\(t\times d_i\)
这样的话我们维护前缀\(t_i\times d_i\)的最大值和后缀\(d_i\)的最大值。这样的话我们就可以选择两种中伤害较大的部分。
如果我们选择\(t\ge t_i\)的情况,那么我们就持续使用\(cnt=t-t_i+1\)次技能。这样造成的伤害最大\(cnt\times t_i\times d_i\),之后就只能使用第二种技能。
如果我们使用第二种技能,我们持续使用$cnt= t-\left \lfloor \frac{max1}{d_i} \right \rfloor \(,其中\)max1\(是第一种能够造成伤害的最大值。这样造成伤害\)d_i\frac{cnt(t+t+1-cnt)}{x}$
#include<bits/stdc++.h>
using namespace std;
#define int __int128
#define ll long long
#define mp make_pair
int read() {
int x = 0, f = 1, ch = getchar();
while ((ch < '0' || ch > '9') && ch != '-') ch = getchar();
if (ch == '-') f = -1, ch = getchar();
while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
return x * f;
}
int32_t main() {
int n = read(), h = read();
vector<pair<int, int>> a(n);
for (auto &[t, d]: a)
t = read(), d = read();
sort(a.begin(), a.end());
vector<pair<int, int> > pre(n);
pre[0] = mp(a[0].first * a[0].second, a[0].first);
for (int i = 1, t; i < a.size(); i++) {
pre[i] = pre[i - 1], t = a[i].first * a[i].second;
if (t > pre[i].first) pre[i] = mp(t, a[i].first);
}
vector<int> suf(n + 1, 0);
for (int i = n - 1; i >= 0; i--)
suf[i] = max(suf[i + 1], a[i].second);
int l = 0, r = h, mid, res;
auto check = [n, h, a, pre, suf](int x) {
int pos = n - 1, cur = h;
while (cur > 0 && x > 0) {
while (pos >= 0 && a[pos].first > x) pos--;
if (pos < 0 || pre[pos].first < suf[pos + 1] * x) {
int down = 0;
if (pos >= 0) down = pre[pos].first / suf[pos + 1];
int cnt = x - down;
int sum = cnt * (x - cnt + 1 + x) / 2 * suf[pos + 1];
cur -= sum, x -= cnt;
} else {
int cnt = x - pre[pos].second + 1;
cur -= cnt * pre[pos].first, x -= cnt;
}
}
return cur <= 0;
};
while (l <= r) {
mid = (l + r) >> 1;
if (check(mid)) res = mid, r = mid - 1;
else l = mid + 1;
}
cout << (ll) res;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号