AtCoder Beginner Contest 297

A - Double Click

#include <bits/stdc++.h>

using namespace std;

#define int long long

int32_t main() {
    int n , d;
    cin >> n >> d;
    vector<int> a(n);
    for( auto & i : a ) cin >> i;
    for( int i = 1 ; i < n ; i ++ ){
        if( a[i] - a[i-1] <= d ){
            cout << a[i];
            return 0;
        }
    }
    cout << "-1\n";
    return 0;
    return 0;
}

B - chess960

#include <bits/stdc++.h>

using namespace std;

#define int long long

int32_t main() {
    string s;
    cin >> s;
    vector<int> v;
    for( int i = 0 ; i < 8 ; i ++ ){
        if( s[i] == 'B' ) v.push_back(i);
    }
    if( v[0] % 2 == v[1] % 2 ){
        cout << "No\n";
        return 0;
    }
    v.clear();
    for( int i = 0 ; i < 8 ; i ++ ){
        if( s[i] == 'K' || s[i] == 'R' )
            v.push_back(i);
    }
    if( s[ v[0] ] != s[ v[2] ] ){
        cout << "No\n";
        return 0;
    }
    cout << "Yes\n";
}

C - PC on the Table

#include <bits/stdc++.h>

using namespace std;

#define int long long

int32_t main() {
    int n , m;
    string s;
    cin >> n >> m;
    while( n -- ){
        cin >> s;
        for( int i = 1 ; i < m ; i ++ ){
            if( s[i] == 'T' && s[i-1] == 'T' )
                s[i-1] = 'P' , s[i] = 'C';
        }
        cout << s << "\n";
    }
}

D - Count Subtractions

过程其实不难理解，反复的做减法直到大小关系改变着可以直接用取模来代替。不过要注意出现倍数的情况，此事要少减一次。

#include <bits/stdc++.h>

using namespace std;

#define int long long

int32_t main() {
    int a, b , cnt = 0;
    cin >> a >> b;
    while (a != b) {
        if( a > b ) cnt += a / b , a %= b;
        else cnt += b / a , b %= a;
        if( min( a , b ) == 0 ) cnt -- , a = b;
    }
    cout << cnt;
}

E - Kth Takoyaki Set

我的写法其实蛮暴力的，用 set 维护前\(k\)小，在维护一个由之前的数产生的数的集合，每次选一个最小的加入到前\(k\)小中。

#include <bits/stdc++.h>

using namespace std;

#define int long long

int read(){
    int x = 0 , f = 1 , ch = getchar();
    while( (ch < '0' || ch > '9') && ch != '-' ) ch = getchar();
    if( ch == '-' ) f = -1 , ch = getchar();
    while( ch >= '0' && ch <= '9' ) x = ( x << 3 ) + ( x << 1 ) + ch - '0' , ch = getchar();
    return x * f;
}

int32_t main() {
    int n = read() , k = read();
    vector<int> a(n);
    set<int>b , c;
    for( int & i : a ) i = read() , b.insert(i);
    for( int x ;c.size() < k ; ){
        x = *b.begin() , b.erase(x);
        c.insert(x);
        for( auto i : a ){
            if( c.count( i + x ) == 0 ) b.insert( i + x );
        }
    }
    cout << *c.rbegin() << "\n";

}

F - Minimum Bounding Box 2

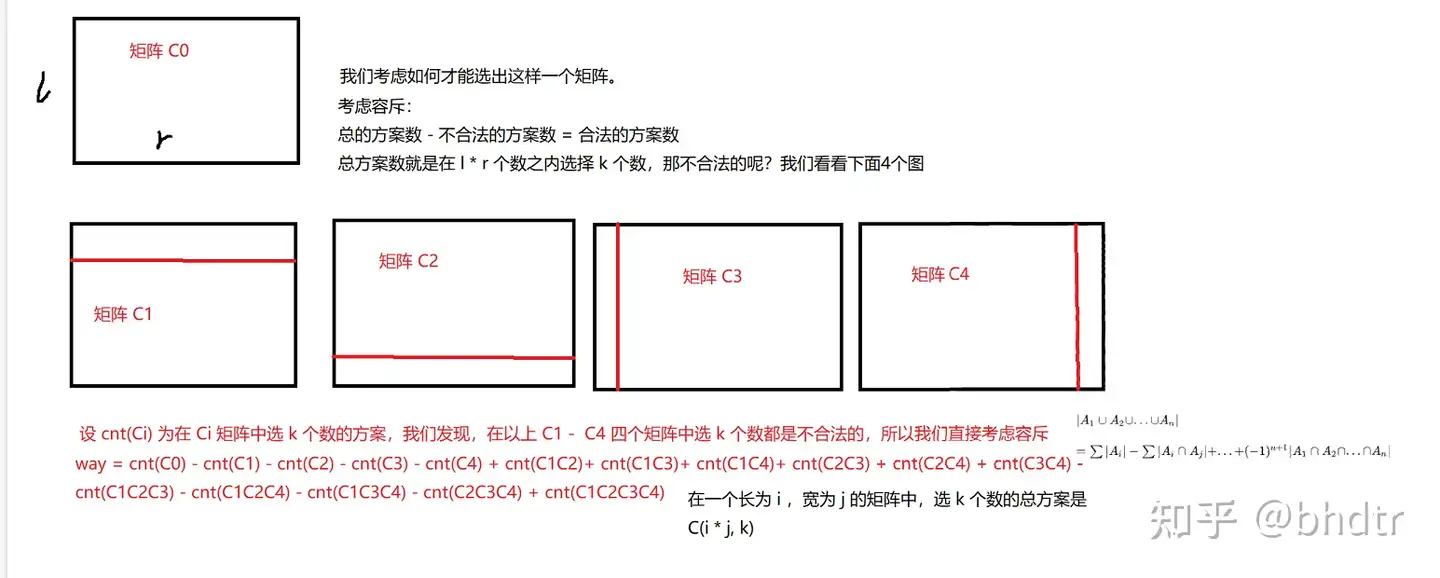
其实就是枚举一下矩形的大小，然后计算出这么大的矩形的贡献，计算贡献采用的是容斥原理。

荣斥可以参考下面的图片，计算方法可以直接用下面这个式子。

\[cnt( l\times r) \\ - 2cnt((l-1)\times r)-2cnt(l\times (r-1))\\ + cnt((l-2)\times r) +cnt(l\times(r-2)) + 4cnt((l-1)\times (r-1)) \\ - 2cnt((l-1)\times(r-2)) - 2cnt((l-2)\times(r-1))\\ + cnt((l-2)\times(r-2)) \]

图片来源

#include <bits/stdc++.h>

using namespace std;

#define int long long
const int N = 1e6 + 5, mod = 998244353;

int fact[N], invFact[N];

int power(int x, int y) {
    int ans = 1;
    while (y) {
        if (y & 1) ans = ans * x % mod;
        y >>= 1, x = x * x % mod;
    }
    return ans;
}

int inv(int x) {
    return power(x, mod - 2);
}

int C(int x, int y) {
    if (x < y) return 0;
    return fact[x] * invFact[x - y] % mod * invFact[y] % mod;
}

void init() {
    fact[0] = 1, invFact[0] = inv(1);
    for (int i = 1; i < N; i++)
        fact[i] = fact[i - 1] * i % mod, invFact[i] = inv(fact[i]);
    return;
}

int32_t main() {
    init();
    int n, m, k;
    cin >> n >> m >> k;
    if (k == 1) {
        cout << "1\n";
        return 0;
    }
    int ans = 0, cnt;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            cnt = 0;
            for (int u = 0; u <= 2; u++)
                for (int v = 0; v <= 2; v++) {
                    cnt += C((i - u) * (j - v), k) * (v == 1 ? -2 : 1) * (u == 1 ? -2 : 1);
                    cnt = (cnt % mod + mod) % mod;
                }
            ans = (ans + i * j % mod * (n - i + 1) % mod * (m - j + 1) % mod * cnt % mod) % mod;
        }
    cout << ans * inv(C(n * m, k)) % mod;
    return 0;
}