CSP-S复习笔记

0x01位运算

与、或、异或

运算符	解释	例子
与`&`	对应位上两个数都为$1$结果为$1$，反之为$0$	`101 & 001 = 001`
或`	`	对应位上两个数有一个为$1$结果为$1$，反之为$0$
异或`^`	对应位上两个数不同为$1$，反之为$0$	`101 ^ 100 = 001`

特别的异或的逆运算还是异或，( a ^ b ) ^ b = a

取反

~一个数的每一位取反，~ 1001 = 0110

注意这里的~是按位取反，!是逻辑取反

左移、右移

左移（>>）把二进制的每一位向左移动，多余的舍弃，右侧补0注意可能会移到符号位上，导致变成负数

右移（<<）把二进制的每一位向右移动，多余的舍弃，左侧补0

注意左移右移的运算优先级低于加减，所以a << 1 + 1 = a << ( 1 + 1 )

位运算的应用

代替乘除

a << i等价于$a \times 2^i$

a >> i等价于$a\div 2^i$

a * 10 = ( a << 3) + ( a << 1 )

集合运算

如果用二进制数来表示集合，还有一些集合运算

操作	集合表示	位运算操作
交集	$a \cap b $	`a & b`
并集	$a \cup b$	`a
补集	$\overline a$	`~ a`

枚举子集

for( register int i = x ; i ; i = ( i - 1 ) & x );

优化常数

下面的写法，在一定程度上可以优化常数

判断奇偶

if( x & 1 ) = if( x % 2 )

交换两个数

inline void swap( int & x , int & y ) { x ^ y ^ x ^ y;}

判断两个数符号是否相同

inline bool isSameSign(int x, int y) {  // 有 0 的情况例外
  return (x ^ y) >= 0;
  // true 表示 x 和 y 有相同的符号，false 表示 x,y 有相反的符号。
}

求平均值

inline int getAverage( int x , int y ) { return (x + y) >> 1; ｝

0x11 栈

栈是一种后进先出的线性数据结构

AcWing 128. 编辑器

开两个栈维护，类似对顶堆的操作，我们把他叫做对顶栈好了

令$P$为光标位置，分别开两个栈$a,b$

栈$a$存$P$之前的数，栈$b存$P$之后的数

$sum$是前缀和，$f$是前缀和的最大值

对于操作$L$，把$x$压入栈$a$并更新$sum$和$f$

对于操作$D$ ，栈$a$栈顶弹出

对于操作$L$，把栈顶$a$弹出并压入栈$b$

对于操作$R$，把栈顶$b$弹出并压入栈$a$同时更新$sum$和$f$

对于操作$Q$，返回$f[x]$

 #include <bits/stdc++.h>
using namespace std;


const int N = 1e6 + 5 , INF = 0x7ffffff;
int T , opt , a[N] , b[N] , sum[N] , f[N] , ta = 0 , tb = 0;

inline int read( bool _ )
{
    register int x = 0 , f_ = 1;
    register char ch = getchar();

    if( _ )
    {
        while( ch < '0' || ch > '9' )
        {
            if( ch == '-' ) f_ = -1;
            ch = getchar();
        }
        while( ch >= '0' && ch <= '9')
        {
            x = ( x << 3 ) + ( x << 1 ) + ch - '0';
            ch = getchar();
        }
        return x * f_;
    }
    else
    {
        while( ch != 'L' && ch != 'R' && ch != 'I' && ch != 'D' && ch != 'Q' ) ch = getchar();
        return int(ch);
    }
}

inline void work_1()
{
    a[ ++ ta ] = read(1);
    sum[ta] = sum[ ta - 1 ] + a[ta];
    f[ta] = max( sum[ta] , f[ ta - 1] );
    return ;
}

inline void work_2()
{
    if( ta > 0 ) ta --;
    return ;
}

inline void work_3()
{
    if( ta > 0 )b[ ++ tb] = a[ ta ] , ta --;
    return ;
}

inline void work_4()
{
    if( !tb ) return ;
    a[ ++ ta ] = b[tb];
    tb --;
    sum[ta] = sum[ta - 1] + a[ta];
    f[ta] = max( sum[ta] , f[ ta - 1] );
    return ;
}

inline void work_5()
{
    printf("%d\n",f[ read(1) ] );
    return ;
}


int main()
{
    f[0] = -INF;
    T = read(1);
    while( T -- )
    {
        opt = read(0);
        if(opt == 'I' ) work_1();
        else if(opt == 'D' ) work_2();
        else if(opt == 'L' ) work_3();
        else if(opt == 'R' ) work_4();
        else work_5();
    }
    return 0;
}

AcWing 131. 直方图中最大的矩形

画图手玩样例就能发现规律

单调栈的经典应用，不过我比较懒，STL+O2直接水过去

#include <bits/stdc++.h>
#pragma GCC optimize(2)
#define LL long long
using namespace std;


const int N = 100005;
int n , now , width ;
LL res;
struct node
{
	int w , h;
}_;
stack< node > s;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline node make( int x , int y )
{
	_.h = x , _.w = y;
	return _;
}


int main()
{
	while( 1 )
	{
		n = read();
		if( !n ) return 0;
		res = 0;
		for( register int i = 1; i <= n ; i ++ )
		{
			now = read();
			if( s.empty() || now > s.top().h ) s.push( make( now , 1 ) );
			else
			{
				width = 0;
				while( !s.empty() && s.top().h > now )
				{
					width += s.top().w;
					res = max( res , (LL)width * s.top().h );
					s.pop();
				}
				s.push( make( now , width + 1 ) );
			}
		}
		width = 0;
		while( !s.empty() )
		{
			width += s.top().w;
			res = max( res , (LL)width * s.top().h );
			s.pop();
		}
		printf( "%lld\n" , res );
	}
	return 0;
}

0x12 队列

队列是一种“先进先出”的线性数据结构，手写队列时可以用循环队列来优化空间

队列还有一些变形体，优先队列，单调队列，双端队列，这些在$STL$中都是有的，不过常数比较大普通队列手写即可

另外优先队列在pbds中也有

AcWing 132. 小组队

这道题本身并不难，只是数据的处理比较恶心

首先开一个队列为维护小组，再开$n$个队列维护每个小组的成员

每次压入一个元素，就把这个元素加入这个小组的队列，如果这个小组的队列是空的就把他加入总的队列

每次弹出一个元素，就把总队列队头的小组弹出一个，如果队头小组的队列此时为空，就把队头小组从总队列总弹出

这道题并不是十分的卡常数，不开$O2$貌似能过，

另外插队不是好习惯，小心被打

#include <bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;


const int N = 1e6 + 5 , M = 1005;
int n , t , m , num , cub[N];
string opt;
map< int , queue<int> > member;
queue< int > team;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 1 ) + ( x << 3 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline void push()
{
	num = read();
	if( member[ cub[num] ].empty() ) team.push( cub[num] );
	member[ cub[num] ].push( num );
	return ;
}

inline void pop()
{
	num = team.front();
	printf( "%d\n" , member[ num ].front() );
	member[ num ].pop();
	if( member[ num ].empty() ) team.pop();
}

inline void work( int k )
{
	n = read();
	if( !n ) exit(0);
	printf( "Scenario #%d\n" , k );

	while( !team.empty() )
	{
		num = team.front();
		while( !member[ num ].empty() ) member[ num ].pop();
		team.pop();
	}
	memset( cub , 0 , sizeof(cub) );

	for( register int i = 1 ; i <= n ; i ++ )
	{
		t = read();
		while( t -- )  cub[ read() ] = i;
	}

	while( 1 )
	{
		cin >> opt;
		if( opt == "ENQUEUE" ) push();
		else if( opt == "DEQUEUE" ) pop();
		else break;
	}
	puts("");
	return ;
}


int main()
{
	for( register int k = 1 ; 1 ; k ++ ) work(k);
	return 0;
}

AcWing 135. 最大子序和

单调队列的基操

首先对于区间和的问题一般情况下都是转发乘前缀和数组，做差即可

然后就是找左右端点的问题

令前缀和数组为$s$

已经枚举的右端点$i$和当前的左端点$j$

此时再任意一个$k$如果满足$k<j<i$且$s[k]>s[j]$，着$k$无论如何也不可能成为最有解，因为对于任意的$i$如果可以选$j$则$j$一定$k$更优

所以我们发现需要维护一个单调递增的序列，并且随着$i$的有移，将会有部分的$j$不能使用

符合单调队列的性质所以用单调队列来维护，队列储存的元素是前缀和数组的下标，队头为$l$，队尾为$r$

对于每次枚举的$i$有以下几个操作

如果$q[l] < i - m$将队头出对
此时的$l$就是最有的$j$更新答案
维护单调队列性质并把$i$放入队列

#include <bits/stdc++.h>
using namespace std;


const int N = 300000;
int n , m , s[N] , q[N] , l  = 1 , r = 1 , res ;


inline int read()
{
	register int x = 0 , f = 1;
	register char ch = getchar();
	while( ch < '0' || ch > '9' )
	{
		if( ch == '-' ) f = -1;
		ch = getchar();
	}
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x * f;
}


int main()
{
	n = read() , m = read();
	for( register int i = 1 ; i <= n ; i ++ ) s[i] = s[i-1] + read();

	for( register int i = 1 ; i <= n ; i ++ )
	{
		while( l <= r && q[l] < i - m ) l ++;
		res = max( res , s[i] - s[ q[l] ] );
		while( l <= r && s[ q[r] ] >= s[i] ) r --;
		q[ ++ r ] = i;
	}
	cout << res << endl;
	return 0;
}

0x13链表与邻接表

数组是一种支持随机访问，但不支持在任意位置插入或删除元素的数据结构

链表支持在任意位置插入或删除，但只能按顺序访问其中的元素

链表的正规形式一般是通过动态分配内存、指针实现，为了避免内存泄漏、方便调试使用数组模拟链表、下标模拟指针也是常见的做法

指针版

struct Node {
	int value; // data
	Node *prev, *next; // pointers
};
Node *head, *tail;

void initialize() { // create an empty list
	head = new Node();
	tail = new Node();
	head->next = tail;
	tail->prev = head;
}

void insert(Node *p, int value) { // insert data after p
	q = new Node();
	q->value = value;
	p->next->prev = q; q->next = p->next;
	p->next = q; q->prev = p;
}

void remove(Node *p) { // remove p
	p->prev->next = p->next;
	p->next->prev = p->prev;
	delete p;
}

void recycle() { // release memory
	while (head != tail) {
		head = head->next;
		delete head->prev;
	}
	delete tail;
}

数组模拟

struct Node {
	int value;
	int prev, next;
} node[SIZE];
int head, tail, tot;

int initialize() {
	tot = 2;
	head = 1, tail = 2;
	node[head].next = tail;
	node[tail].prev = head;
}

int insert(int p, int value) {
	q = ++tot;
	node[q].value = value;
	node[node[p].next].prev = q;
	node[q].next = node[p].next;
	node[p].next = q; node[q].prev = p;
}

void remove(int p) {
	node[node[p].prev].next = node[p].next;
	node[node[p].next].prev = node[p].prev;
}


// 邻接表：加入有向边(x, y)，权值为z
void add(int x, int y, int z) {
	ver[++tot] = y, edge[tot] = z; // 真实数据
	next[tot] = head[x], head[x] = tot; // 在表头x处插入
}

// 邻接表：访问从x出发的所有边
for (int i = head[x]; i; i = next[i]) {
	int y = ver[i], z = edge[i];
	// 一条有向边(x, y)，权值为z
}

AcWing 136. 邻值查找

首先我们开一个pair记录$A_i$和对应的$i$

然后排序，并用一个链表维护这个序列，链表的值是每个数字排序后的位置

所以每个链表的前驱就是小于等于这个数中最大的，后继就是大于等于这个数中最小的

然后我们倒着访问从$n$开始，因为这样不管是前驱还是后继在原序列中的位置一定比当前数在原序列中的位置跟靠前

做差比较、记录结果

然后删掉当前这个数字，因为剩下的数字在原序列中都比他靠前，所以这个数字一定不会是其他数字的结果

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 1e5 + 5 , INF = 0x7f7f7f7f;
int n , l[N] , r[N] , p[N];
pair< int ,int > a[N] , res[N];


inline int read()
{
	register int x = 0,f = 1;
	register char ch = getchar();
	while(ch < '0' || ch > '9')
	{
		if( ch == '-' ) f = -1;
		ch = getchar();
	}
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x * f;
}

int main()
{
	n = read();
	for( register int i = 1 ; i <= n ; i ++ )
	{
		a[i].first = read();
		a[i].second = i;
	}
	
	sort( a + 1 , a + 1 + n );
	
	a[0].first = -INF , a[ n + 1 ].first = INF;
	
	for( register int i = 1 ; i <= n ; i ++ ) l[i] = i - 1 ,  r[i] = i + 1 , p[ a[i].second ] = i;
	
	for( register int i = n ; i > 1 ; i -- )
	{
		register int j = p[i] , L = l[j] , R = r[j] ;
		register LL l_val = abs( a[L].first - a[j].first ) , r_val = abs( a[R].first - a[j].first );
		if( l_val <= r_val ) res[i].first = l_val , res[i].second = a[L].second;
		else res[i].first = r_val , res[i].second = a[R].second;
		l[R] = L , r[L] = R;
	}
	
	for( register int i = 2 ; i <= n ; i ++ ) printf( "%d %d\n" , res[i].first , res[i].second );
	
	return 0;
}

0x14 Hash

Hash 表

Hash表又称散列表，一般有Hash函数与链表结构共同构成

Hash表主要包括两个基本操作

计算Hash函数的值
定位到对应的链表中依次遍历、比较

常用的的Hash函数是$H(x) = (x\mod \ p)+ 1$

这样显然可以把所有的数分成$p$个，如果遇到冲突情况，用链表维护即可

AcWing 137. 雪花雪花雪花

设计Hash函数为$H(a_1,a_2,\cdots,a_6) = (\sum^{6}_{i=1}a_i + \Pi^{6}_{i=1}a_i)\ mod\ p$,其中$p$是一个我们自己选择的一个大质数

然后我们依次把每个雪花插入Hash表中，在对应的链表中查找是否已经有相同的雪花

判断是否有相同雪花的方式就是直接暴力枚举就好

#include <bits/stdc++.h>
using namespace std;


const int N = 100010,p = 9991;
int n ,head[N] , nxt[N] ,snow[N][6], tot;


inline int  H( int *a )
{
	int sum = 0 , mul = 1 ;
	for( register int i = 0 ; i < 6 ; i ++ ) sum = ( sum + a[i] ) % p , mul = ( ( long long )mul * a[i] ) % p;
	return ( sum + mul ) % p;  
}

inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline bool equal( int *a, int *b)
{
	for( register int i = 0 ; i < 6 ; i ++ )
	{
		for( register int j = 0 ; j < 6 ; j ++ )
		{
			bool eq = 1;
			for( register int k = 0 ; k < 6 && eq; k ++ )
			{
				if( a[ ( i + k ) % 6 ] != b[ ( j + k ) % 6 ] ) eq = 0; 
			}
			if( eq ) return 1;
			eq = 1;
			for( register int k = 0 ; k < 6  && eq; k ++ )
			{
				if( a[ ( i + k ) % 6 ] != b[ ( j - k + 6 ) % 6 ] ) eq = 0;
			}
			if ( eq ) return 1;
		}
	}
	return 0;
} 

inline bool insert( int *a )
{
	register int val = H( a );
	for( register int i = head[val] ; i ; i = nxt[i] )
	{
		if(equal(snow[i] , a ) ) return 1;
	}
	++ tot;
	memcpy( snow[tot] , a , 6 * sizeof( int ) );
	nxt[ tot ] = head[val];
	head[val] = tot;
	return 0;
}


int main()
{
	n = read();
	int a[10];
	
	for( register int j = 1 ; j <= n ; j ++ )
	{
		for( register int i = 0 ; i < 6 ; i ++ ) a[i] = read();
		if( !insert( a ) ) continue;
		puts( "Twin snowflakes found." );
		exit(0); 
	}
	
	puts( "No two snowflakes are alike." );
	return 0;
}

字符串Hash

下面介绍的字符串$Hash$函数把任意一个长度的支付串映射成一个非负整数，并且冲突的概率近乎为$0$

取一固定值$P$，把字符串看成是$P$进制数并且分配一个大于$0$的数值，代表每种字符。一般说，我们分配的数值都远小于$P$。例如，对于小写字母构成的字符串，可以令$a=1,b=2,\dots ,z = 26$。取一固定值M,求出该P进制数对M取的余数，作为该字符的$Hash$值。

一般来说，我们取$P=131$或$P=13331$，此时$Hash$值产生的冲突概率极低，通常我们取$M=2^{26}$，即直接使用$unsigned\ long\ long$的自然溢出来代替低效率的取模运算。

但是在极端构造的数据中取模会导致$Hash$冲突，所以可以采用链表来存下每个字符串，也可以通过多次$Hash$来解决

AcWing 140. 后缀数组

这道题是字符串Hash，首先把原字符串的前缀进行Hash

然后用一个数组来代表后缀，通过$O(1)$计算得到后缀的Hash

然后在比较时，我们通过二分，二分出两个后缀的最大公共前缀，我们只需比较公共前缀的下一位就可以比较两个后缀的字典序

#include <bits/stdc++.h>
#define ULL unsigned long long
#define H( l , r ) ( h[r] - h[ l - 1 ] * p[ r - l + 1 ] ) 
using namespace std;


const int N = 300010 , base = 131;
int n ,sa[N];
ULL h[N] , p[N];
char str[N];


inline ULL get_max_common_prefix( int a , int b )
{
	int l = 0 , r = min( n - a + 1 , n - b + 1 );
	while( l < r )
	{
		int mid = l + r + 1 >> 1;
		if( H( a , a + mid - 1 ) != H( b , b + mid - 1 ) ) r = mid - 1;
		else l = mid;
	}
	return l;
}

inline bool cmp( int a , int b)
{
	register int l = get_max_common_prefix( a , b );
	register int av = a + l > n ? INT_MIN : str[ a + l ];
	register int bv = b + l > n ? INT_MIN : str[ b + l ]; 
	return av < bv;
}


int main()
{
	scanf( "%s" , str + 1 );
	n = strlen( str + 1 );
	
	p[0] = 1 ;
	for( register int i = 1 ; i <= n ; i ++ )
	{
		p[i] = p[ i - 1 ] * base;
		h[i] = h[ i - 1 ] * base + str[i] - 'a'  + 1 ;
		sa[i] = i;
	}
	
	sort( sa + 1 , sa + 1 + n , cmp );
	
	for( register int i = 1 ;i <= n ; i ++ ) printf("%d " , sa[i] - 1 );
	puts("");
	
	for( register int i = 1; i <= n ;i ++ )
	{
		if( i == 1 ) printf( "0 " );
		else printf( "%d " , get_max_common_prefix( sa[ i - 1 ] , sa[i] ) );    
	}
	puts("");
	
	return 0;
}

0x15 字符串

KMP模式匹配

$KMP$算法，又称模式匹配算法，能够在线性时间内判定字符串$A[1\dots N]$是否是字符串$B[1\dots M]$的子串，并求出字符串$A$在字符串$B$中出现的位置

KMP算法分为两步

对字符串A进行自我匹配，求出一个数组$next$，其中$next[i]$表示“$A$中以$i$结尾的非前缀子串”与“$A$的前缀”能够匹配的最长长度，即：

$next[i] = max\{ j \}$,其中$j<i$且$A[i-j+1\dots i] = A[1\dots j]$

特别地，当不存在这样的$j$时$next[i] = 0$
对于字符串$A$与$B$进行匹配，求出一个数组$f$,其中$f[i]$表示“$B$中以$i$结尾的子串”与“$A$的前缀”能够匹配的最长长度，即：

$f[i] = max\{ j \}$,其中$j\le i$且$B[i-j+1\dots i] = A[1\dots j]$

$KMP$算法$next$数组的求法

next[1] = 0;
for( register int i = 2 , j = 0 ; j <= n ; i ++ )
{
		while( j && a[i] != a[ j + 1 ] ) j = next[j];
		if( a[i] == a[ j + 1 ] ) j ++ ;
		next[i] = j; 
}

$KMP$算法$f$数组的求法

for( register int i = 1 , j = 0 ; i <= m ; i ++ )
{
		while( j && ( j == n || b[i] != a[ j + 1 ] ) ) j = next[j];
		if( b[i] == a[ j + 1 ] ) j ++;
		f[i] = j;
		if( f[i] == n ) //此时就是A在B中间出现一次
}

CF1029A

这道题实际上就是一道啊很简单的$KMP$模板题，理解下$KMP$里$next$数组的作用就明白了

先输出原序列，在把$t[next[n]\cdots n]$输出$k-1$次就好

#include <bits/stdc++.h>
using namespace std;


const int N = 60;
int n , k , nxt[N];
char t[N];

int main()
{
	cin >> n >> k;
	scanf( "%s" , t + 1 );
	
	nxt[1] = 0;
	for( register int i = 2 , j = 0 ;i <= n ; i ++ )
	{
		while( j && t[i] != t[ j + 1 ] ) j = nxt[j];
		if( t[i] == t[j + 1] ) j ++ ;
		nxt[i] = j ;
	}	

	printf( "%s" , t + 1 );
	
	for( ; k > 1 ; k -- ) 
	{
		for( register int i = nxt[n] + 1 ; i <= n ; i ++ ) printf( "%c" , t[i] );
	}
	puts("");
	return 0;
}

最小表示法

给定一个字符串$S[1\dots n]$,如果我们不断的把它的最后一个字符放到开头，最终会得到$n$个字符串，称这$n$个字符串是循环同构的。这些字符串中字典序最小的一个称为字符串$S$的最小表示法

算法流程

初始化i=1，j=2
通过直接先后扫描的方法比较 b[i]与b[j]两个循环同构串。
- 如果扫描了n个字符后仍然相等，说明s有更小的循环元（例如catcat有循环元cat）,并且该循环元以扫描完成，B[min(i,j)]即为最小表示，算法结束
- 如果在i+k与j+k处发现不想等：
  - 若ss[i+k]>ss[j+k],令i=i+k+1。若此时i=j，再令i=i+1
  - 若ss[i+k]<ss[j+k]，令j=j+k+1。若此时i=j，再令j=j+1
若i>n或j>n，则B[min（i，j)]为最小表示；否则重复第二步

int  n = strlen( s + 1 ); 
for( register int i = 1 ; i <= n ; i ++ ) s[ n + i ] = s[i];
int i = 1 , j = 2 , k;
while( i <= n && j <= n )
{
	for( k = 0 ; k < n && s[ i + k ] == s[ j + k ] ; k ++ );
	if( k == n ) break;//s形如 catcat ，它的循环元以扫描完成
	if( s[ i + k ] > s[ j + k ] )
	{
		i += k + 1;
		if( i == j ) i ++;
	}
	else 
	{
		j += k + 1;
		if( i == j ) j ++; 
	}
}
ans = min( i , j ); //B[ans]是s的最小表示

Luogu P1368

看题目，简单分析就知道是落得最小表示法

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 300005 * 2 ;
int n , ans;
LL a[N];


inline LL read()
{
	register LL x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline void mini_notation()
{
	register int i = 1 , j = 2 , k;
	while( i <= n && j <= n )
	{
		for( k = 0 ; k < n && a[ i + k ] == a[ j + k ] ; k ++ );
		if( k == n ) break;
		if( a[ i + k ] <= a[ j + k ] )
		{
			j += k + 1;
			if( i == j ) j ++;
		}
		else
		{
			i += k + 1;
			if( i == j ) i ++;
		}
	}
	ans = min( i , j );
}


int main()
{
	n = read();
	for( register int i = 1 ; i <= n ; i ++ ) a[ i + n ] = a[i] = read();
	
	mini_notation();
	
	for( register int i = ans , j = 1 ; j <= n ; i ++ , j ++ ) printf( "%lld " , a[i] );
	puts("");
	return 0;
	
}

0x16 Trie

Trie，又称字典树，是一种用于实现字符串快速检索的多叉树结构。Trie的每个节点都拥有若干个字符指针，若在插入或检索字符串时扫描到一个字符c,就沿着当前节点的这个字符指针，走向该指针指向的节点。

Trie的节点可以使用一个结构体进行储存，如下代码中，trans[i]表示这个节点边上的之父为i的边到达儿子节点的编号，若为0则表示没有这个儿子节点

struct node
{
	int trans[z];// z为字符集的大小
	bool bo;// 若bo = true 则表示这个顶点代表的字符串是集合中的元素 
}tr[N];

现在要对一个字符集的Trie插入一个字符串s

inline void insert(string s)
{
	register int len = s.size(),u = 1;
	for(register int i = 0;i < len;i ++)
	{
		if(!tr[u].trans[s[i] - 'a']) tr[u].trans[s[i] - 'a'] = ++ tot;
		//若不存在这条边则要建立一个新的节点 tot为总的点数 
		u = tr[u].trans[s[i] - 'a']; 
	}
	tr[u].bo = 1; //在结尾表示它代表的字符串是集合中的一个元素 
	return ;
}

查询一个字符串s是否在集合中某个串的前缀

inline bool search(string s)
{
	register int len = s.size(),u = 1;
	for(register int i = 0;i < len; i ++)
	{
		if(!tr[u].trans[s[i] - 'a']) return 0;
		u = tr[u].trans[s[i] - 'a'];
	}
	return 1;
}

查询一个字符串s是否是集合中的一个元素

inline bool query(string s)
{
	register int len = s.size(),u = 1;
	for(register int i = 0;i < len; i ++)
	{
		if(!tr[u].trans[s[i] - 'a']) return 0;
		u = tr[u].trans[s[i] - 'a'];
	}
	return tr[u].bo;
}

AcWing 142. 前缀统计

构建一颗$tire$树在每个结点存一个$cn$t记录以当前节点为结尾的字符串有多少个

然后在遍历$tire$树将$cnt$求和即可

#include <bits/stdc++.h>
#define I( x ) ( x - 'a' )
using namespace std;


const int N = 1e6 + 5 , Z = 30;
int n , m , tot = 1 , len , u , ans ;
string s;

struct node
{
	int cnt , trans[Z];
}tr[N];


inline void insert()
{
	len = s.size() , u = 1;
	for( register int i = 0 ; i < len ; i ++ )
	{
		if( !tr[u].trans[ I( s[i] ) ] ) tr[u].trans[ I( s[i] ) ] = ++ tot;
		u = tr[u].trans[ I( s[i] ) ];
	}
	tr[u].cnt ++;
	return ;
}

inline int search()
{
	len = s.size() , u = 1 ,ans = 0;
	for( register int i =  0 ; i < len ; i ++ )
	{
		if(!tr[u].trans[ I( s[i] ) ] ) return ans;
		u = tr[u].trans[ I( s[i] ) ];
		ans += tr[u].cnt;
	}
	return ans;
}


int main()
{
	cin >> n >> m;
	for( register int i = 1 ; i <= n ; i ++ ) 
	{
		cin >> s;
		insert();
	}
	
	for( register int i = 1 ; i <= m ; i ++ )
	{
		cin >> s;
		cout << search() << endl;	
	}
	
	return 0;
}

AcWing 143.最大异或对

要写这道题首先要了解一些位运算的相关知识

首先我们可以构建一个$01tire$，把所有的数字转化成二进制插入

然后我们枚举一下每一个数字，然后去$01tire$中查找，查找每一位时，首先查找是否有和当前位相反的，如果有就选择

这样查找完后，得到二进制数就是所有数字中和当前数异或值最大的，对所有的最大值取$max$即可

观察发现，我们可以一遍建树，一边查找，效果是一样的

#include <bits/stdc++.h>
using namespace std;


const int N = 1e5 + 5;
int n , a[N] , tot = 1 , res = -1;

struct Trie
{
	int to[2];
}t[ N * 32 ];


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 1 ) + ( x << 3 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline void insert( int x )
{
	register int u = 1 , s;
	for( register int i = 30 ; i >= 0 ; i -- )
	{
		s = x >> i & 1 ;
		if( !t[u].to[s] ) t[u].to[s] = ++ tot;
		u = t[u].to[s];
	}
}
 
inline int search( int x )
{
	register int u = 1 , ans = 0 , s;
	for( register int i = 30 ; i >= 0 ; i -- )
	{
		s =  x >> i & 1;
		if( t[u].to[ s ^ 1 ] ) u = t[u].to[ s ^ 1 ] , ans |= 1 << i;
		else u = t[u].to[s];
	}
	return ans;
}


int main()
{
	n = read();
	
	for( register int i = 1 ; i <= n ; i ++ ) a[i] = read() , insert( a[i] ) , res = max( res , search( a[i] ) );
	
	cout << res << endl;

	return 0;
}

0x17 二叉堆

二叉堆是一种支持插入、删除、查询最值的数据结构。它其实是一颗满足“堆性质”的完全二叉树

二叉树的实现可以手写，当然我自己跟推荐使用STL，当然pbds也可以

priority_queue

构造

priority_queue< int > q;//大根堆
priority_queue< int , vector< int > , greater< int > > q;//小根堆

注意priority_queue中储存的元素类型必须定义“小于号”，较大的元素会被放在堆顶。内置的int、string等类型已经定义过“小于号”，若使用结构体则必须重载运算符

由于priority_queue是按照从大到小排序所以重载运算符时也要反过来

struct node
{
	int value ;
	friend bool operator < (node a , node b)
	{
		return a.value > b.value;
	}
};

成员函数

q.top();\\访问堆顶元素
q.empty();\\检查是否为空
q.size();\\返回容纳的元素数
q.push();\\插入元素，并排序
q.pop();\\删除栈顶元素

懒惰删除法

如果是手写的堆是支持删除任意一个元素，而$STL$却不支持这种操作所以我们可以用懒惰删除法

懒惰删除法又称延迟删除法，是一种应对策略。当遇到删除操作时，仅在优先队列之外做一些特殊的记录，用于辨别是否堆中的元素被删除。当从堆顶取出元素时判断是否已经被删除，若是，我们重新取一个最值。换言之，元素的“删除”推迟到堆顶执行

比如“堆优化的$Dijkstra$算法”中当某个元素首次被取出时就达到了最短路，当我们再次取出这个元素时我们不会重新进行扩展，而是使用一个$bool$数组判断“是否进行过扩展”，其本质还是懒惰删除法的应用

我们发现,当$A$序列和$B$序列从小到大排序后,最小和肯定是$A[1]+B[1]$,而次小和必然是$min(A[2]+B[1],A[1]+B[2])$,也就是说当我们确定好$A[i][j]$为$K$小和的话,那么第$k+1$小的和,必然是$min(A[k+1]+B[k],A[k]+B[k+1])$,既然如此的话,我们还要注意一点,$A[1]+B[2]$和$A[2]+B[1]$都可以推导出$A[2]+B[2]$,所以说我们要记得,如果说$j+1$了,那么i就不要$+1$了,避免出现重叠,导致答案错误.至于$min$函数,可以使用小根堆来维护当前最小值.

数学的归纳法,我们就可以从$2$,推到$N$的情况,也就是先求出前两个序列的值,然后推出前$N$小的和的序列,然后用这个退出来的序列,再和第三个序列求值,然后同理,再得出来的值与第四个序列进行同样的操作

#include <bits/stdc++.h>
using namespace std;


const int N = 2010;
int t , n , m , a[N] , b[N] , c[N] , tot;

struct node
{
	int i , j;
	bool f;
	friend bool operator < ( node x , node y )
	{
		return a[ x.i ] + b[ x.j ] > a[ y.i ] + b[ y.j ];
	}

}cur , temp ;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 1 ) + ( x << 3) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline node make_node( int i , int j , bool f )
{
	cur.i = i , cur.j = j , cur.f = f;
	return cur;
}

inline void work()
{
	sort( b + 1 , b + 1 + m );
	priority_queue< node > q;
	tot = 0;
	
	q.push( make_node( 1 , 1 , 0 ) );
	for( register int i = 1 ; i <= m ; i ++)
	{
		temp = q.top() , q.pop();
		c[i]  = a[ temp.i ] + b[ temp.j ];
		q.push( make_node( temp.i , temp.j + 1 , 1 ) );
		if( !temp.f ) q.push( make_node( temp.i + 1 , temp.j , 0 ) );
	}
	memcpy( a , c , sizeof( a ) );
	return ;
}


int main()
{
	
	t = read();
	while(t--)
	{
		n = read() , m = read();
		for( register int i = 1 ; i <= m ; i ++ ) a[i] = read();
		sort( a + 1 , a + 1 + m );	
		
		for( register int i = 2 ; i <= n ; i ++ )
		{
			for( register int j = 1 ; j <= m ; j ++ ) b[j] = read();
			work();
		}
	
		for( register int i = 1 ; i <=  m  ; i ++ ) printf( "%d " , a[i] );
		puts("");	
	}
	return 0;
}

AcWing 147. 数据备份

Luogo P3620 数据备份

这是一道贪心+链表+堆的题

对于题面其实很好理解，就是有$n$个点，$n-1$条边，从中选$k$个但是每个节点只能选一次，求边权最小和

首先我们求$k = 1$时的情况，即所有边中最小的一个

再看$k=2$的情况，首先我们选择的所有中最小的一个即为$i$

呢么第二条选的不是$i-1$，或$i+1$则无影响

若第二条边选的时$i-1$则$i+1$必选，也就是放弃$i$

因为如果选$i-1$，不选$i+1$选$j$的情况下，此时对$i$时没有限制的则必有$v[i]+v[k]\le v[i-1]+v[k]$

如果$k=3$，举下面这个例子

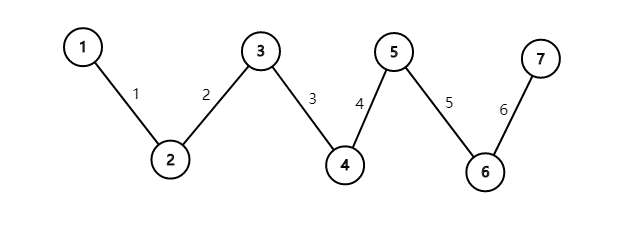
假设已经选择的$2$和$4$

此时我们要选择$1$则必选$3$和$5$

如果不选$3,5$，选$3,6$的话

则必有$1,4,6$比$1,3,6$更优

根据数学归纳法我们可以推出，如果我们已经选择一串连续的点构成的边，假如我们因为要选择某一条边来破坏某一条边已经被选择的边，呢么这些连续的点构成的边一定要全部都破坏不然不可能更优

知道这个结论后在结合贪心的策略就可以解决这个问题

首先我们用一个堆来维护所以的边首先取出一个边$i$，把$v[i]$累加的答案中，并且在堆中加入条权值为$v[i-1]+v[i+1]-v[i]$，左端点为$i-1$的左端点，右端点为$i+1$的右端点的边，并且删除$i-1$和$i+1$这两条边

这样当我们选择的到$i-1$或$i+1$时都会选择到这条新加入边，对位边的信息我们用双向链表来维护即可

对于堆的删除操作可以使用懒惰标记法，这里给出一个$set$解决的方法，并会在下一小节给出set的基本用法

#include <bits/stdc++.h>
#define LL long long
#define PLI pair< LL , int >
using namespace std;


const int N = 100010;
int n , k , l[N] , r[N];
LL d[N] , res;
set< PLI > s;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}


inline void delete_node( int p )
{
	r[ l[p] ] = r[p] , l[ r[p] ] = l[p];
}



int main()
{
	n = read() , k = read();
	for( register int i = 1 ; i <= n ; i ++ ) d[i] = read();
	for( register int i = n ; i > 0 ; i -- ) d[i] -= d[ i - 1 ];
	d[1] = d[ n + 1 ] = 1e15;
	
	for( register int i = 1 ; i <= n ; i ++ )
	{
		l[i] = i - 1;
		r[i] = i + 1;
		s.insert( { d[i] , i } );
	}
	
	while( k -- )
	{
		set< PLI >::iterator it = s.begin();
		register LL v = it -> first;
		register int p = it -> second , left = l[p] , right = r[p];
		s.erase(it) , s.erase( { d[left] , left } ) , s.erase( { d[right] , right } );
		delete_node(left) , delete_node(right);
		res += v;
		d[p] = d[left] + d[right] - d[p];
		s.insert( { d[p] , p } ) ;
	}
	
	cout << res << endl;
	return 0;
}

set

set< int > s;//构造函数,元素不可重复 
multiset<int>s;//构造函数，元素可以重复 
s.size();//返回s中有多少元素 
s.empty();//返回s是否为空 
s.clear();//清空s 
s.begin();//返回指向s中第一个元素的迭代器 
s.end();//返回指向s中最后一个元素下一个位置的迭代器 
s.insert(x);//向s中插入一个元素x 
s.find(x);//返回s中指向x的迭代器，如果s中没有x则返回s.end() 
s.erase(x);//删除x 
s.count(x)//返回s中x元素的个数（这个只适用于multiset）

Huffman 树

考虑这样一个问题：构造一颗包含$n$个节点的$k$叉树，其中第$i$个叶子节点的权值为$w_i$，要求最小化$\sum w_i \times l_i$其中$l_i$表示第$i$个叶子节点到根节点的距离

该问题被称为Huffman树（哈夫曼树）

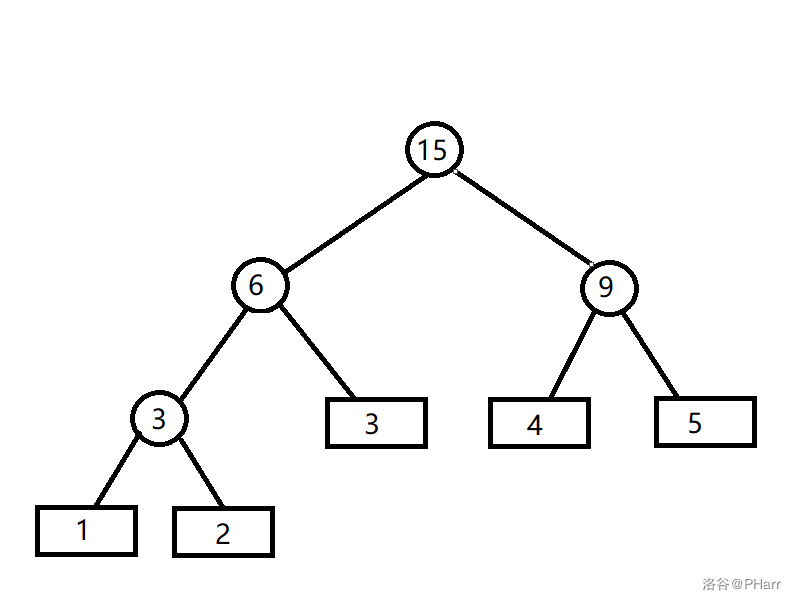
为了最小化$\sum w_i \times l_i$，应该让权值打的叶子节点的深度尽量的小。当$k=2$时，我们很容易想到用下面这个贪心思路求$Huffman$树

建立一个小根堆,插入这$n$个叶子节点的权值
从队列中取出两个最小的权值$w_1$和$w_2$，令$ans += w_1 + w_2$
建立一个权值为$w_1 + w_2$的树节点$p$，并把$p$成为$w_1$和$w_2$的父亲节点
在堆中插入$p$节点
重复$2 \cdots 4$，直到堆的大小为$1$

对于$k>2$的$Huffman$树，正常的想法就是在上述算法上每次取出$k$的节点

但加入最后一次取不出$k$个时，也就是第一层未满，此时从下方任意取出一个子树接在根节点的下面都会更优

所以我们要进行一些操作

我们插入一些额外的权值为$0$的叶子节点，满足$(n-1)mod(k-1) = 0$

这是在根据上述思路做即可，因为补$0$后只有最下面的一次是不满的

AcWing 148. 合并果子

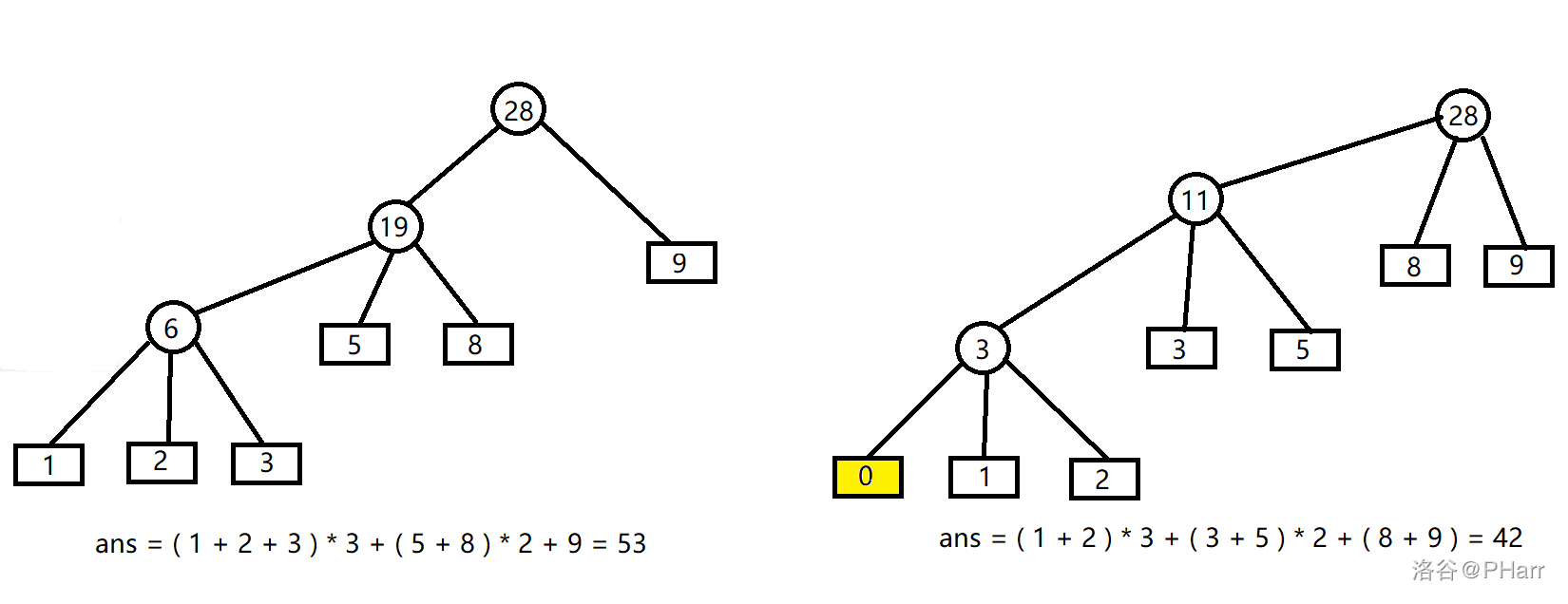
$2$叉$Huffman$树模板题，直接做即可

#include <bits/stdc++.h>
using namespace std;

int n , ans , a , b;
priority_queue< int , vector<int> , greater<int> > q; 


inline int read()
{
    register int x = 0;
    register char ch = getchar();
    while( ch < '0' || ch > '9' ) ch = getchar();
    while( ch >= '0' && ch <= '9' )
    {
        x = ( x << 1 ) + ( x << 3 ) + ch - '0';
        ch = getchar();
    }
    return x;
} 


int main()
{
    n = read();
    for( register int i = 1 ; i <= n ; i ++ ) q.push( read() );
    while( q.size() > 1 )
    {
        a = q.top() , q.pop() , b = q.top() , q.pop();
        ans += a + b;
        q.push( a + b );
    }
    cout << ans << endl;
    return 0;
}

AcWing 149. 荷马史诗

这道题目背景比多，有考阅读的成分

简化版的提议就是求$Huffman$树，并且求出$Huffman$树的深度

所以只需稍作更改即可

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair< LL, int> PLI;


int n , m ;
LL res; 
priority_queue< PLI , vector<PLI> , greater<PLI> > heap;


inline LL read()
{
	register LL x = 0 , f = 1;
	register char ch = getchar();
	while( ch < '0' || ch > '9' )
	{
		if( ch == '-' ) f = -1;
		ch = getchar();
	}
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x * f;
}


int main()
{
	n = read() , m = read();
	for( register int i = 1 ; i <= n ; i ++ ) heap.push( { read() , 0 } );
	
	while( ( n - 1 ) % ( m - 1 ) ) heap.push( { 0ll , 0 } ) , n ++;
	
	while( heap.size() > 1 )
	{
		register LL sum = 0;
		register int depth = 0;
		for( register int i = 0 ; i < m ; i ++ ) sum += heap.top().first , depth = max( depth , heap.top().second ) , heap.pop();
		res += sum;
		heap.push( { sum , depth + 1 } );
	}
	
	cout << res << '\n' << heap.top().second << '\n';
	return 0;
}

0x21 树与图的遍历

树与图的深度优先遍历

深度优先遍历，就是在每个点$x$上面的的多条分支时，任意选择一条边走下去，执行递归，直到回溯到点x后再走其他的边

int head[N];
bool v[N];
struct edge
{
	int v , next;
}e[N];

inline void dfs( int x )
{
	v[x] = 1;
	for( register int i = head[x] ; i ; i = e[i].next)
	{
		register int y = e[i].next;
		if( v[y] ) continue;
		dfs( y ) ;
	}
	return ;
}

树的DFS序

一般来说，我们在对树的进行深度优先时，对于每个节点，在刚进入递归时和回溯前各记录一次该点的编号，最后会产生一个长度为$2N$的序列，就成为该树的$DFS$序

$DFS$序的特点时：每个节点的$x$的编号在序列中恰好出现两次。设这两次出现的位置时$L[x]$,$R[x]$，那么闭区间$[L[x],R[x]]$就是以$x$为根的子树的$DFS$序

inline void dfs( int x )
{
	a[ ++ tot ] = x; // a储存的是DFS序
	v[ x ] = 1;
	for( register int i = head[x] ; i ; i = e[i].next )
	{
		register int y = e[i].v;
		if( v[y] ) continue;
		dfs( y );
	}
	a[ ++ tot ] = x;
	return ;
}

树的深度

树中各个节点的深度是一种自顶向下的统计信息

起初，我们已知根节点深度是$0$.若节点$x$的深度为$d[x]$,则它的节点$y$的深度就是$d[y] = d[x] + 1$

inline void dfs( int x )
{
	v[ x ] = 1;
	for( register int i = head[ x ] ; i ; i = e[i].next )
	{
		register int y = e[i].v;
		if( v[ y ] ) continue;
		d[ y ] = d[ x ] + 1; // d[]就是深度
		dfs( y );
	}
	return ;
}

树的重心

对于一个节点$x$，如果我们把它从树中删除，呢么原来的一颗树可能会被分割成若干个树。设$max\_part(x)$表示在删除节点$x$后产生子树中最大的一颗的大小。使$max\_part(p)$最下的$p$就是树的重心

inline void dfs( int x )
{
	v[ x ] = 1 , size[ x ] = 1;//size 表示x的子树大小 
	register int max_part = 0; // 记录删掉x后最大一颗子树的大小 
	for( register int i = head[ x ] ; i ; i = e[i].next )
	{
		register int y = e[i].v;
		if( v[y] ) continue;
		dfs( y );
		size[x] += size[y];
	} 
	max_part = max ( max_part , n - size[x] );
	if( max_part < ans ) //全局变量ans记录重心对应的max_part 
	{ 
		ans = max_part;
		pos = x;//pos 重心 
	}
	return ;
}

图的联通块划分

若在一个无向图中的一个子图中任意两个点之间都存在一条路径（可以相互到达），并且这个子图是“极大的”（不能在扩展），则称该子图是原图的一个联通块

如下代码所示，cnt是联通块的个数，v记录的是每一个点属于哪一个联通块

inline void dfs( int x )
{
	v[ x ] = cnt;
	for( register int i = head[x] ; i ; i = e[i].next ) 
	{
		register int y = e[i].v;
		if( v[y] ) continue;
		dfs(y);
	}
	return ;
}

for( register int i = 1 ; i < = n ; i ++ )
{
	if( v[i] ) continue;
	cnt ++ ;
	dfs( i );
}

图的广度优先搜索遍历

树与图的广度优先遍历是利用一个队列来实现的

queue< int  > q;

inline void bfs()
{
	q.push( 1 ) , d[1] = 1;
	while( !q.empty() )
	{
		register int x = q.front(); q.pop();
		for( register int i = head[ x ] ; i ; i = e[i].next )
		{
			register int y = e[i].v;
			if( d[y] ) continue;
			d[y] = d[x] + 1;
			q.push(y);
		} 
	}
	return ;
}

上面的代码中，我们在广度优先搜索中顺便求了个树的深度$d$

拓扑排序

给定一张有向无环图，若一个序列A满足图中的任意一条边(x,y)x都在y的前面呢么序列A就是图的拓扑排序

求拓扑序的过程非常简单我们只需要不断将入度为0的点加入序列中即可

建立空拓扑序列A
预处理出所有入度为deg[i],起初把入度为0的点入队
取出对头节点x,并把x放入序列A中
对于从x出发的每条边(x,y)，把deg[y]减1，若deg[y] = 0 ,把y加入队列中
重复3，4直到队列为空，此时A即为所求

inline void addedge( int x , int y )
{
	e[ ++ tot ].v = y , e[ tot ].next = head[x] , head[x] = tot;
	deg[x] ++;
} 

inline void topsort()
{
	queue< int > q;
	for( register int i = 1 ; i <= n ; i ++ )
	{
		if( !deg[i] ) q.push( i );
	} 
	while( !q.empty() )
	{
		register int x = q.front(); q.pop();
		a[ ++ cnt ] = x;
		for( register int i = head[x] ; i ; i = e[i].next )
		{
			register int y = e[i].v;
			if( -- deg[y] == 0 ) q.push( y );
		}
 	}
 	return ;
}

AcWing 164. 可达性统计

这道题的题意很简单，但是如果直接裸的计算会超时，所以要用拓扑序

首先求拓扑序，因为拓扑序中的每一个点都时由前面的点到的所以我们反过来从最后一个点开始

假设我们已经求得了$x$后面每一个点的所能到达的点，呢么我们对所有以x为起点的边所到达的点所能到达的点取并集就是$x$所等到达的所有的点

然后如果们要储存每个点所到达的点，如果我们用二维数组来存，会爆空间，所以为了节约空间可以用<bitset>来存

#include <bits/stdc++.h>
using namespace std;

const int N = 30010;
int n , m , head[N] , d[N]  , a[N] , tot , cnt ; 
bitset< N > f[N];

struct edge
{
	int v , next;
}e[N];


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 1 ) + ( x << 3 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline void addedge( int u , int v )
{
	e[ ++ tot ].v = v , e[ tot ].next = head[u] , head[u] = tot;
	d[ v ] ++;
}

inline void topsort()
{
	queue< int > q;
	for( register int i = 1 ; i <= n ; i ++ )
	{
		if( !d[i] ) q.push( i );
	}
	while( !q.empty() )
	{
		register int x = q.front(); q.pop();
		a[ ++ cnt ] = x;
		for( register int i = head[x] ; i ; i = e[i].next )
		{
			register int y = e[i].v;
			if( -- d[y] == 0 ) q.push( y );
		}
	}
	return ;
}


int main()
{
	n = read() , m = read();
	for( register int i = 1 ; i <= m ; i ++ )
	{
		register int a = read() , b = read();
		addedge( a , b );
	}
	
	topsort();
	
	for( register int i = cnt , j = a[i] ; i ; i -- , j = a[i] )
	{
		f[j][j] = 1;
		for( register int k = head[j] ; k ; k = e[k].next ) f[j] |= f[ e[k].v ];
	}
	
	for( register int i = 1 ; i <= n ; i ++ ) printf( "%d\n" , f[i].count() );
	return 0;
}

0x22 深度优先搜索

深度优先搜索算法$(Depth-First-Search)$是一种用于遍历或搜索树或图的算法

沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点$v$的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

AcWing 165. 小猫爬山

这道题时dfs最基础的题目了

我们只需设计搜索的状态这道题就可以轻易的写出来

我们设(x,y)是搜索的状态即前x个小猫用了y个缆车

我们要转移的情况只有两种

小猫上前y辆缆车
小猫上y+1辆缆车（新开一辆）

所以我们只要枚举就好

然后就是如何优化算法

首先假如我们已经得到一个解pay,若此时的大于pay则不可能会更优，所以可以自己而回溯

然后我们把小猫从大到小排序可以排除很多不可能是结果的情况

#include <bits/stdc++.h>
using namespace std;


const int N = 20;
int n , w , c[N] , f[N], pay = N;

inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	} 
	return x;
}

inline void dfs( int x , int y )
{
	if( x > n )
	{
		pay = min( pay , y );
		return ;
	}
	if( y > pay ) return ;
	
	for( register int i = 1 ; i <= y ; i ++ )
	{
		if( f[i] + c[x] > w ) continue;
		f[i] += c[x];
		dfs( x + 1 , y );
		f[i] -= c[x];
	}
	y ++;
	f[y] += c[x];
	dfs( x + 1 , y );
	f[y] = 0;
	return ;
}

inline bool cmp( int x , int y ) { return x > y; }


int main()
{
	n = read() , w = read();
	for( register int i = 1 ; i <= n ; i ++ ) c[i] = read();
	
	sort( c + 1 , c + 1 + n , cmp );
	dfs( 1 , 0 );
	
	cout << pay << endl;
	return 0;
}

AcWing 166. 数独

这是一道经典的搜索题，不过是数据加强过的版本，所有直接搜索会T

必须要进行一些优化

首先我们想自己玩数独的时候是怎么玩的

肯定是首先填可能的结果最少的格子，在也是这道题优化的核心

如何快速的确定每个格子的情况？

const int n = 9;
int row[n] , col[n] , cell[3][3];
// row[] 表示行 col表示列 cell[][] 表示格子

我们用一个九位二进制数来表示某一行、某一列、或某一个中可以填入的数，其中1表示可以填，0表示不能填

对于$(x,y)$这个点我们只需$row[x] \bigcap col[y] \bigcap cell[\frac{x}{3}][\frac{y}{3}]$就可以知道这个点可以填入数字的集合然后用lowbit()把每一位取出来即可

而在二进制中的交集就是$& $操作，所以取交集的函数就是

inline int get( int x , int y )
{
	return row[ x ] & col[ y ] & cell[ x / 3 ][ y / 3];
}

还有什么优化呢，lowbit()的时间复杂度是$O(log(n))$我们可以通过预处理把一些操作变成$O(1)$的

首先每次lowbit()得到的并不是最后一个一定位置而是一个二进制数，可以用这个maps[]，$O(1)$查询最后一为的具体位置

for( register int i = 0 ; i < n ; i ++ ) maps[ 1 << i ] = i;

其次对于每个二进制数中有多少个$1$的查询也是很慢的，可以用这个ones[]，$O(1)$查询一个二进制数中有多少个$1$

for( register int i = 0 , s = 0 ; i < 1 << n ; i ++  , s = 0)
{
	for( register int j = i ; j ; j -= lowbit( j ) ) s ++;
	ones[ i ] = s;
}

剩下就是常规的$DSF$

#include <bits/stdc++.h>
#define lowbit( x ) ( x & -x )
using namespace std;


const int N = 100 , n = 9;
int maps[ 1 << n ] , ones[ 1 << n ] , row[n] , col[n] , cell[3][3];
char str[N];


inline void init() //初始化 
{
	for( register int i = 0 ; i < n ; i ++ ) row[i] = col[i] = ( 1 << n ) - 1 ;
	for( register int i = 0 ; i < 3 ; i ++ )
	{
		for( register int j = 0 ; j < 3 ; j ++ ) cell[ i ][ j ] = ( 1 << n ) - 1;
	}
}

inline int get( int x , int y ) //取交集 
{
	return row[ x ] & col[ y ] & cell[ x / 3 ][ y / 3];
}

inline bool dfs( int cnt )
{
	if( !cnt ) return 1; // 已经填满 
	
	register int minv = 10 , x , y;
	for( register int i = 0 ; i < n ; i ++ )
	{
		for( register int j = 0 ; j < n ; j ++ )
		{
			if( str[ i * 9 + j ] != '.' ) continue;
			register int t = ones[ get( i , j ) ];
			if( t < minv ) // 找到可能情况最少的格子 
			{
				minv  = t;
				x = i , y = j ;
			}
		}
	}
	
	for( register int i = get( x , y ) ; i ; i -= lowbit( i ) ) // 枚举这个格子填那些数 
	{
		register int t = maps[ lowbit(i) ];
		row[x] -= 1 << t , col[y] -= 1 << t; // 打标记 
		cell[ x / 3 ][ y / 3 ] -= 1 << t;
		str[ x * 9 + y ] = t + '1';
		
		if( dfs(cnt - 1 ) ) return 1;
		
		row[x] += 1 << t , col[y] += 1 << t; // 删除标记 
		cell[ x / 3 ][ y / 3 ] += 1 << t;
		str[ x * 9 + y ] = '.';
	}
	return 0;
}


int main()
{
	for( register int i = 0 ; i < n ; i ++ ) maps[ 1 << i ] = i;
	for( register int i = 0 , s = 0 ; i < 1 << n ; i ++  , s = 0)
	{
		for( register int j = i ; j ; j -= lowbit( j ) ) s ++;
		ones[ i ] = s; // i 这个数二进制中有多少个 1 
	}
	
	while( cin >> str , str[0] != 'e' )
	{
		init();
		
		register int cnt = 0;
		for( register int i = 0 , k = 0 ; i < n ; i ++ )
		{
			for( register int j = 0 ; j < n ; j ++ , k ++ )
			{
				if(str[k] == '.' ) { cnt ++ ; continue; } //记录有多少个数字没有填 
			
				register int t = str[k] - '1'; // 把已经填入的数字删除 
				row[ i ] -= 1 << t;
				col[ j ] -= 1 << t;
				cell[ i / 3 ][ j / 3 ] -= 1 << t;
			}
		}
		
		dfs( cnt );
		
		cout << str << endl;
	}
		
	return 0;
}

0x23 剪枝

剪枝，就是减小搜索树的规模、尽早的排除搜索树中不必要的成分

优化搜索顺序
在一些问题中，搜索树的各个层次、各个分支的顺序是不固定的。不同的搜索顺序会产生不同的搜索树形态，其规模相差也很大。我们可以通过优先搜索更有可能出现结果的分支来提前找到答案
排除等效冗余
在搜索的过程中，如果能够判定搜索树上当前节点的几个分支是等效的，这我们搜索其中一个分支即可
可行性剪枝
在搜索的过程中对当前的状态进行检查，如果无论如何都不可能走到边界我们就放弃搜索当前子树，直接回溯
最优性剪枝
在搜索过程中假设我们已经找到了某一个解，如果我们目前的状态比已知解更劣就放弃继续搜索下去因为无法比当前解更优呢么后面情况累加起来后一定比当前解更劣，所以直接回溯
记忆化
可以记录每个状态的结果，在每次遍历过程中检查当前状态是否已经被访问过，若果被访问过直接返回之前搜索的结果

AcWing 167.木棒

这是一道经典的剪枝题

优化搜索顺序

把木棍从大到小排序，优先尝试比较长的木棍，越短的木棍适应能力越强

排除等效冗余

限制加入木棍的顺序必须是递减的，因为假如有两根木棍$x,y(x<y)$，先加入$x$和先加入$y$是等效的
如果上一根木棍失败且和当前木棍长度相同，这当前木棍一定失败
如过当前木棍已经拼成一个完整的木棍，当后面拼接过程中失败则当前木棍无论怎么拼都一定会失败，因为在重新尝试的过程中会使用更多更小的木棍来拼成当前木棍，但更小的木棍的适用性更强，却失败了，所以用更长的木棍尝试也一定会失败

#include <bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#pragma GCC optimize(2)
using namespace std;


const int N = 100;
int n , m , a[N] , sum , cnt , len ;
bool v[N];


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline bool cmp( int x , int  y ) { return x > y; }

inline bool dfs( int stick , int cur , int last)
{
	if ( stick == cnt ) return 1;
	if ( cur == len ) return dfs( stick + 1 , 0 , 1 );
	
	register int fail = 0;
	for (register int i = last; i <= n; i++) // 剪枝 2  
	{
		if( v[i] || cur + a[i] > len || fail == a[i] ) continue;
		// fail == a[i] 剪枝 3 
		v[i] = 1;
		if ( dfs( stick , cur + a[i] , i + 1 ) ) return 1;
		v[i] = 0 , fail = a[i];
		if ( cur == 0 || cur + a[i] == len ) break;
		// cur + a[i] = len 剪枝 4 
	}
	return 0; 
}

inline void work()
{ 
	sum = n = 0;
	for( register int i = 1 ; i <= m ; i ++ )
	{
		register int x = read();
		if( x > 50 ) continue;
		a[ ++ n ] = x , sum += x;
	}
	
	sort( a + 1 , a + 1 + n , cmp );
	//剪枝 1 
	
	for( len  = a[1] ; len <= sum ; len ++ )
	{
		if( sum % len ) continue;
		cnt = sum / len;
		memset( v , 0 , sizeof( v ) );
		if( dfs( 1 , 0 , 1 ) ) break;
	}
	printf( "%d\n" , len );
	return ;
}


int main()
{
	while(1)
	{
		m = read();
		if( m == 0 ) break;
		work();
	}
	return 0;
}

0x24 迭代加深

深度优先搜索（$ID-DSF$）就是每次选择一个分支，然后不断的一直搜索下去，直到搜索边界在回溯，这种算法有一定的缺陷

比如下面这张图，我要红色点走到另一个红色点

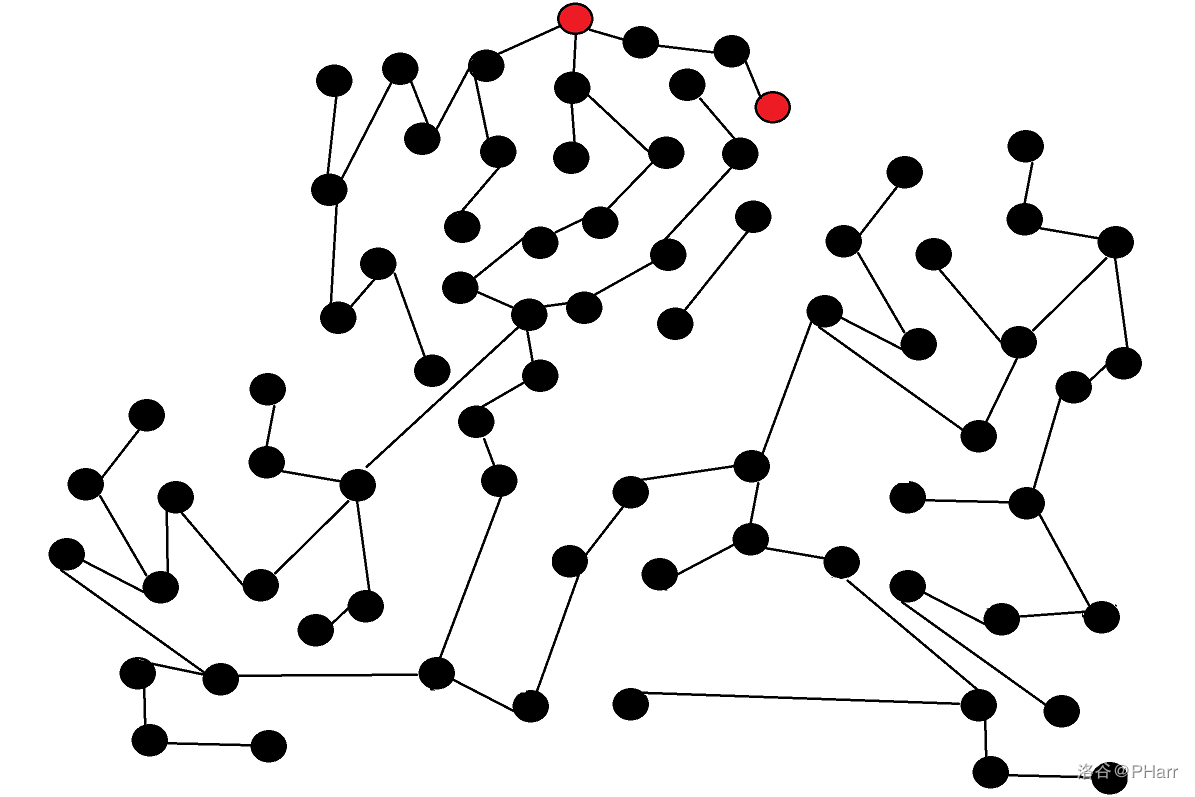
如果用普通的$DFS$前面的很多状态都是无用的，因为子树太深了

并且每到一个节点我都要储存很多的东西$BFS$很不好存

这是就要用到迭代加深了

AcWing 170. 加成序列

这道题就是一个迭代加深搜索的模板题

为什么是迭代加深搜索呢？

分析题目给的性质

如果使用$DFS$，你需要搜索很多层，并且第一个找到的解不一定最有解

如果使用$BFS$，你需要在队列中储存$M$个长度为$n$的数组($M$是队列长度)，不仅储存非常麻烦并且还有可能会爆栈

所以通过迭代加深性质就能很好的解决这个问题

限制序列的长度，不断从已知的数中找两个相加，到边界时判断一下，比较常规

优化搜索顺序

为了能够尽早的达到$n$,从大到小枚举$i$，$j$

排除等效冗余

因为$i$，$j$和$j$，$i$是等效的所以保证$j \le i$
不同的$i$,$j$可能出现$a[i]+a[j]$相同的情况，对相加结果进行判重

#include <bits/stdc++.h>
using namespace std;


const int N = 105;
int n , m , a[N];
bitset< N > vis;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' ) 
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline bool ID_dfs( int k )
{
	if( k > m ) return a[m] == n;
	
	vis.reset();
	for( register int i = k - 1 ; i > 0 ; i -- )
	{
		for( register int j = k - 1 ; j > 0 ; j -- )
		{
			register int cur = a[i] + a[j];
			if( cur > n || vis[ cur ] || cur < a[ k - 1 ]) continue;
			a[k] = cur;
			vis[ cur ] = 1;
			if( ID_dfs( k + 1 ) ) return 1;
		}
	}
	return 0;
}

inline void work()
{
	for( m = 1 ; m <= n ; m ++ )
	{
		if( ID_dfs( 2 ) ) break;
	}
	for( register int i = 1 ; i <= m ; i ++ ) printf( "%d " , a[i] );
	puts("");
	return ;
}


int main()
{
	a[1] = 1 , a[2] = 2;
	for( n = read() ; n ; n = read() ) work();
	return 0;
}

双向搜索

除了迭代加深外，双向搜索也可以大大减少在深沉子树上浪费时间

在一些问题中有明确的初始状态和末状态，呢么就可以采用双向搜索

从初状态和末状态出发各搜索一半，产生两颗深度减半的搜索树，在中间交汇组合成最终答案

AcWing 171.送礼物

这到题显然是一个$DP$，但是由于它数字的范围非常大做$DP$肯定会$T$

所以这道题的正解就是$DFS$暴力枚举所有可能在判断

但是$n\le 46$所以搜索的复杂度是$O(2^{46})$依然会$T$

所以还是要想办法优化，这里用了到了双向搜索的思想

我们将$a[1\cdots n]$,分成$a[1\cdots mid]$和$a[mid+1\cdots n]$两个序列

首先现在第一个序列中跑一次$DFS$求出所以可以产生的合法情况，去重，排序

然后在第二个序列中再跑一次$DFS$，求出的每一个解$x$就在第一序列产生的结构中二分一个$y$满足$max(x),x\in\{ x | x + y \le W \}$，更新答案

优化

优化搜索顺序，从大到小搜索，很常规
我们发现第二次$DFS$中会多次二分，所以我们可以适当的减少第二个序列长度，来平衡复杂度。换句话来说就是适当的减少二分的次数，根据实测$mid=\frac{n}{2}+2$效果最好

#include <bits/stdc++.h>
using namespace std;


const int N = 50;
int w , n ,tot , a[N] , mid , ans , m ;
vector < int > s;


inline int read()
{
    register int x = 0;
    register char ch = getchar();
    while( ch < '0' || ch > '9' ) ch = getchar();
    while( ch >= '0' && ch <= '9' )
    {
        x = ( x << 3 ) + ( x << 1 ) + ch - '0';
        ch = getchar();
    }
    return x;
}

inline void dfs_1( int x , long long sum )
{
    s.push_back( sum );
    if( x > mid ) return ;
    if( sum + a[x] <= w ) dfs_1( x + 1 , sum + a[x] );
    dfs_1( x + 1 , sum );
    return ;
}

inline void dfs_2( int x , long long sum )
{
    register auto t = lower_bound( s.begin() , s.end() , w - sum , greater<int>() );
    if( sum + *t <= w ) ans = max( ans , I(sum) + *t );
    if( x > n ) return ;
    if( sum + a[x] <= w ) dfs_2( x + 1 , sum + a[x] );
    dfs_2( x + 1 , sum );
    return ;
}


int main()
{
    w = read() , m = read() ; 
    for( register int i = 1 ; i <= m ; i ++ )
    {
        register int x = read();
        if( x > w ) continue;
        a[ ++ n ] = x;
    }

    mid = n >> 1 + 2;
    sort( a + 1 , a + 1 + n , greater<int>() );
    dfs_1( 1 , 0 );
    sort( s.begin() , s.end() );
    unique( s.begin() , s.end() );
    dfs_2( mid + 1 , 0);
    cout << ans << endl;
    return 0;
}

0x25 广度优先搜索

$BFS$ 全称是 $Breadth First Search$ ，中文名是宽度优先搜索，也叫广度优先搜索。

是图上最基础、最重要的搜索算法之一。

所谓宽度优先。就是每次都尝试访问同一层的节点。如果同一层都访问完了，再访问下一层。

这样做的结果是，$BFS$ 算法找到的路径是从起点开始的最短合法路径。换言之，这条路所包含的边数最小。

在 $BFS$ 结束时，每个节点都是通过从起点到该点的最短路径访问的。

算法过程可以看做是图上火苗传播的过程：最开始只有起点着火了，在每一时刻，有火的节点都向它相邻的所有节点传播火苗。

AcWing 172. 立体推箱子

这到题是宽搜中比较有难度的一道

这道题中不变的是图，变化的是物体的状态，所以本题的难点就在于如何设计状态

我们可以用一个三元组$(x,y,lie)$来代表一个状态（搜索树上的一个节点）

当$lie=0$时，物体立在$(x,y)$上

当$lie=1$时，物体横向躺着，并且左半部分在$(x,y)$上

当$lie=2$时，物体纵向躺着，并且上半部分在$(x,y)$上

并且用数组$d[x][y][lie]$表述从其实状态到每个状态所需要的最短步数

设计好状态就可以开始搜索了

#include <bits/stdc++.h>
using namespace std;


const int N = 510;
const int dx[4] = { 0 , 0 , 1 , -1 } , dy[4] = { 1 , -1 , 0 , 0 };
const int next_x[3][4] = { { 0 , 0 , -2 , 1 } , { 0 , 0 , -1 , 1 } , { 0 , 0 , -1 , 2 } }; 
const int next_y[3][4] = { { -2 , 1 , 0 , 0 } , { -1 , 2 , 0 , 0 } , { -1 , 1 , 0 , 0 } }; 
const int next_lie[3][4] = { { 1 , 1 , 2 ,  2 } , { 0 , 0 , 1 , 1 } , { 2 , 2 , 0 , 0 } }; 
int n , m , d[N][N][3] , ans;
char s[N][N]; 
struct rec{ int x , y , lie; } st , ed ; //状态
queue< rec > q;


inline bool valid( int x , int y ) { return x >= 1 && x <= n && y >= 1 && y <= m; }

bool operator == (rec a ,rec b ){ return a.x == b.y && a.y == b.y && a.lie == b.lie ;}

inline void pares_st_ed()
{
	for( register int i = 1 ; i <= n ; i ++ )
	{
		for( register int j = 1 ; j <= m ; j ++ )
		{
			if( s[i][j] == 'O')	ed.x = i , ed.y = j , ed.lie = 0, s[i][j] = '.';
			else if( s[i][j] == 'X' )
			{
				for( int k = 0 ; k < 4 ; k ++ )
				{
					register int x = i + dx[k] , y = j + dy[k];
					if( valid( x , y ) && s[x][y] == 'X' )
					{
						st.x = min( i , x ) , st.y = min( j , y ) , st.lie = k < 2 ? 1 : 2;
						s[i][j] = s[x][y] = '.';
						break;
					}
				}
			}
			if( s[i][j] == 'X' ) st.x = i , st.y = j , st.lie = 0;
		} 
	}
}

inline bool check( rec next )
{
	if( !valid( next.x , next.y ) ) return 0;
	if( s[next.x][next.y] == '#' ) return 0;
	if( next.lie == 0 && s[next.x][next.y] != '.' ) return 0;
	if( next.lie == 1 && s[next.x][next.y] == '#' ) return 0;
	if(	next.lie == 2 && s[next.x][next.y] == '#' ) return 0;
	return 1; 
} 

int bfs() {
	for( register int i = 1 ; i <= n ; i ++ )
	{
		 for( register int j = 1 ; j <= m ; j ++ )
		 {
		 	for( register int k = 1 ; k <= n ; k ++ ) d[i][j][k] = -1;
		 }
	}
	
	while( q.size() ) q.pop();
	d[st.x][st.y][st.lie] = 0 ; 
	q.push( st );
	rec now , next;
	
	while( q.size() )
	{
		now = q.front() , q.pop();
		for( int i = 0 ; i < 4; i ++ )
		{
			next.x = now.x + next_x[now.lie][i] , next.y = now.y + next_y[now.lie][i] , next.lie = next_lie[now.lie][i];
			if (!check(next)) continue;
			
			if (d[next.x][next.y][next.lie] == -1) 
			{  
				d[next.x][next.y][next.lie] = d[now.x][now.y][now.lie]+1;
				q.push(next);
				if (next.x == ed.x && next.y == ed.y && next.lie == ed.lie) return d[next.x][next.y][next.lie];  // 到达目标
			}
		}
	}
	return -1; 
}


int main()
{
	while( 1 )
	{
		cin >> n >> m;
		if( !n && !m ) break;
		
		for( register int i = 1 ; i <= n ; i ++ ) scanf( "%s" , s[i] + 1 );
		pares_st_ed();
		ans = bfs();
		if( ans == -1 ) puts("Impossible");
		else cout << ans << endl;
	}
	return 0;
}

在上述的代码中使用了$next\_x,next\_y,next\_lie$这三个数组来表示向四个方向移动的变化情况时宽搜中常用的一中技巧，避免了大量使用$if$语句容易造成混乱的情况

Luogu P3456 GRZ-Ridges and Valleys

这道题时一个宽搜的经典题，如果用$DFS$会爆栈

看代码就可以理解

#include<bits/stdc++.h>
using namespace std;


const int N = 1005;
const int dx[8] = { -1 , -1 , -1 , 0 , 0 , 1 , 1 , 1 } , dy[8] = { -1 , 0 , 1 , -1 , 1 , -1 , 0 , 1 };
//向 8 个方向扩展
int n , maps[N][N] , valley , peak;
bool vis[N][N] , v , p;
struct node
{
	int x , y;
} _ , cur;// 储存搜索状态
queue< node > q;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
} 

inline node make_node( int x , int y ) { _.x = x , _.y = y; return _; }


inline int bfs()
{
	register int ux , uy;
	while( !q.empty() )
	{
		cur = q.front() , q.pop();
		for( register int i = 0 ; i <= 7 ; i ++ )
		{
			ux = cur.x + dx[i] , uy = cur.y + dy[i];
			if( ux < 1 || ux > n || uy < 1 || uy > n ) continue;
			//判断是否跃出边界	
			if( maps[ux][uy] == maps[ cur.x ][ cur.y ] && !vis[ux][uy] )
			{//如果高度相同，打标记继续搜索
				vis[ux][uy] = 1;
				q.push( make_node( ux , uy ) );
			}
			else//判断当前联通块是 山峰 或 山谷
			{
				if( maps[ux][uy] > maps[cur.x][cur.y] ) p = 0;
				if( maps[ux][uy] < maps[cur.x][cur.y] ) v = 0;
			}
		}
	}
}	 


int main()
{
	n = read() , v = 1;
	for( register int i = 1 ; i <= n ; i ++ )
	{
		for( register int j = 1 ; j <= n ; j ++ )
		{
			maps[i][j] = read();
			if( maps[i][j] != maps[1][1] ) v = 0; 
		}
	}
	
	if( v ) puts("1 1") , exit(0);//特殊情况判断
	
	for( register int i = 1 ; i <= n ; i ++ )
	{
		for( register int j = 1 ; j <= n ; j ++ )
		{
			if( vis[i][j] ) continue;//判断当前点是否是被搜索的联通块
			v = p = vis[i][j] = 1;
			q.push( make_node( i , j ) );
			bfs();
			peak += p , valley += v;
		}
	}
	
	cout << peak << ' ' << valley << endl;
	return 0;
}

0x26广搜变形

双端队列$BFS$

双端队列 $BFS$ 又称 $0-1 BFS$

适用范围

在一张图中，如果一张图中，有些边有边权，有些边没有边权，如果要搜索这个图，就要用双端队列$BFS$

具体实现

在搜索过程中，如果遇到的没有边权的边就加入队头，如果有边权就加入队尾

AcWing 175. 电路维修

可以把这张方格图，抽象成点，然后把图中有的边当成边权为$1$，把没有的边当作没有边权的边

然后做双端队列$BFS$就好

#include <bits/stdc++.h>
#define PII pair< int , int >
using namespace std;


const int N = 510 , INF = 0x7f7f7f7f;
const int dx[4] = { -1 , -1 , 1 , 1 } , dy[4] = { -1 , 1 , 1 , -1 };
const int ix[4] = { -1 , -1 , 0 , 0 } , iy[4] = { -1 , 0 , 0 , -1 };
int n , m , T , t , d[N][N];
bool vis[N][N];
char g[N][N] , cs[] = "\\/\\/";


inline int bfs()
{
	deque< PII > q;
	memset( vis , 0 , sizeof( vis ) );
	memset( d , INF , sizeof( d ) );
	d[0][0] = 0;
	q.push_back( { 0 , 0 } );
	
	while( !q.empty() )
	{
		auto cur = q.front() ; q.pop_front();
		register int x = cur.first , y = cur.second;
		if( vis[x][y] ) continue;
		vis[x][y] = 1;
		
		for( register int i = 0 ; i < 4 ; i ++ )
		{
			register int a = x + dx[i] , b = y + dy[i];
			register int j = x + ix[i] , k = y + iy[i];
			if( a >= 0 && a <= n && b >= 0 && b <= m)
			{ 
				register int w = 0;
				if( g[j][k] != cs[i] ) w = 1;
				if( d[a][b] > d[x][y] + w )
				{
					d[a][b] = d[x][y] + w;
					if( w ) q.push_back( { a , b } );
					else q.push_front( { a , b } );
				}
			}
		}
	}
	if( d[n][m] == INF ) return -1;
	return d[n][m];
}

inline void work()
{
	cin >> n >> m;
	for( register int i = 0 ; i < n ; i ++ ) scanf( "%s" , g[i] );
	
	t = bfs();
	
	if( t == -1 ) puts("NO SOLUTION");
	else printf( "%d\n" , t );
	return ;
}


int main()
{
	cin >> T;
	while( T -- ) work();
	return 0;
}

优先队列$BFS$

这里就是利用优先队列的性质，每次优先扩展最优的状态

AcWing 176. 装满的油箱

这题要用到优先队列，因为普通的DFS会超时的

首先我们使用一个二元组$\{city,fuel\}$来表示一个状态，每个状态的权值就是到达这个状态所需要的权值

然后们把所有的状态都放入一个堆中，并且按照权值从小到大排序

每次我们去除堆顶的元素进行扩展

如果当前油箱还没有满，就扩展$\{city,fuel+1\}$这个状态
遍历以当前边为起点的所有边，如果当前油箱的油可以到达下一个城市，就扩展$\{v , fuel -d[city][v\}$这个状态

所以当我们第一次从对头取出终点,就是最优解

#include <bits/stdc++.h>
#define F first
#define S second
using namespace std;


const int N = 1005 , C  = 105 , INF = 0x7f7f7f7f;
int n , m , T , c , st , ed , tot , a[N] , head[N] , dist[N][C];
bool vis[N][C];
priority_queue< pair< int , pair< int , int > > > q;
vector< pair< int , int > > e[N];


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}



inline void work()
{
	c = read() , st = read() , ed = read();
	while( !q.empty() ) q.pop();
	memset( vis , 0 , sizeof( vis ) );
	memset( dist , INF , sizeof( dist ) );
	
	dist[ st ][0] = 0;
	q.push( make_pair( 0 , make_pair( st , 0 ) ) );
	
	while( !q.empty() )
	{
		register int city = q.top().S.F , fuel = q.top().S.S;
		q.pop();
		if( city == ed )
		{
			cout << dist[city][fuel] << endl;
			return ;
		}
		
		if( vis[city][fuel] ) continue;
		vis[city][fuel] = 1;
		if( fuel < c && dist[city][fuel + 1 ] > dist[city][fuel] + a[city] )
		{
			dist[city][ fuel + 1 ] = dist[city][fuel] + a[city];
			q.push(make_pair( - dist[city][fuel] - a[city], make_pair( city , fuel + 1 ) ) );
		}
		for( auto it : e[city] )
		{
			register int y = it.F , z = it.S;
			if( z <= fuel && dist[y][ fuel - z ] > dist[city][fuel] )
			{
				dist[y][ fuel - z ] = dist[city][fuel];
				q.push(make_pair( - dist[city][fuel] , make_pair( y , fuel - z ) ) );
			}
		}
	}
	puts("impossible");
}


int main()
{
	n = read() , m = read();
	for( register int i = 0 ; i < n ; i ++ ) a[i] = read();
	for( register int i = 1 ; i <= m ; i ++ )
	{
		register int u = read() , v = read() , w = read();
		e[u].push_back( make_pair( v , w ) );
		e[v].push_back( make_pair( u , w ) );
	}
	
	T = read();
	while( T -- ) work();
	
	return 0;
}

双向$BFS$

双向BFS的思想和0x24中双向搜索是相同的，因为BFS是逐层搜索，所以会更好理解，同时算法实现也很简单

从起始状态，目标状态分别开始，两边轮流进行，每次各扩展一层。当两边各自有一个状态在记录数组中发生重复时，就说明搜索过程中相遇，可以合并各自出发点到当前的最少步数

//开始结点 和 目标结点 入队列 q
//标记开始结点为 1
//标记目标结点为 2
while( !q.empty() )
{
    //从 q.front() 扩展出新的s个结点
  	//如果 新扩展出的结点已经被其他数字标记过
    //那么 表示搜索的两端碰撞
    //那么 循环结束
	
    //如果 新的s个结点是从开始结点扩展来的
    //那么 将这个s个结点标记为1 并且入队q 

  	//如果 新的s个结点是从目标结点扩展来的
    //那么 将这个s个结点标记为2 并且入队q
}

0x27 A*

注：本小结在叙述过程中使用参照了$cdcq$和$thu$的$ppt$,所以一些概念与我们常规的定义略有冲突

在之前的优先队列$BFS$中，我们通过记录从起始状态到当前状态的权值$W$,并且按照$W$排序，这样可以减少许多不必要的搜索

这其实就是一种贪心的思想，如果遇到当前的权值比较小，但后面的权值非常大，此时在用这种套路就会增加很多不必要的搜索

所以也就有了启发式搜索$A$，首先我们要定义一些符号方便理解

s//初始状态
t//目标状态
n//当前状态
g*[n] //从 s 到 n 的最小代价
h*[n] //从 n 到 t 的最小代价
f*[n] = h*[n] + g*[n]//从 s 到 t 的最小代价

对于每个状态,我们按照他的$f[n]$排序，每次取出最优解，扩展状态，直到第一次扩展到$t$，结束循环

虽然$A$算法保证一定可以最先找到最优解，但多数时候会因为求$h^*[n]$，会耗费很大的代价，导致时间复杂度变大

所以就有了另一种算法最佳图搜索算法$A^*$，还是我们要定义一些符号

g[n] // g*[n] 的估计值 ，但是由于我们已经访问到当前状态所以g[n] == g*[n] 
h[n] // h*[n] 的估计值
f[n] = h[n] + g[n] // f*[n] 的估计值 称为估价函数

只要保证$h[n] \le h^*[n]$，剩余不变$A$算法就变成了$A^*$算法

可以简单的叙述下正确性，因为$h[n] \le h^*[n]$，即使估计函数不太准确，导致路径上的非最有状态被提前扩展

但是由于$g[n]$不断累加，$f[n]$会不段的逼近$f^*[n]$，所以最先扩展到状态时一定还是最优解，因为$h[t]==0$

另外如果$h[n]=0$的话，$A^*$算法就变成了优先队列$BFS$,所以优先队列$BFS$就是估价函数不够优秀的$A^*$算法

所以如何设计一个优秀的估价函数就是$A^*$算法的精髓

AcWing 178. 第K短路

听说因为数据比较水，所以可以$dijkstra$第$k$次弹出也可以过

$A^*$的题都没什么好说的，只要知道怎么设计估价函数其他就是模板了

我们看估价函数的定义式$h[x]=f[x]+g[x]$

我们发现$g[x]$是关键，$g[x]$的定义就是从当前状态的步数到目标状态的可能步数，且必须保证$g[x]\le g^*[x]$

不难想到求个最短路就好了，不过要求的是多源单汇最短路，且图是个有向图，用$floyed$也是不合适的

所以我们可以在反向图上跑从T出发的单源多汇最短路的值作为$g[x]$即可

#include <bits/stdc++.h>
#define PII pair< int , int >
#define IPII pair< int , PII > 
#define F first
#define S second
using namespace std;


const int N = 1005 , INF = 0x7f7f7f7f ; 
int n , m , vis[N] , g[N] , st , ed , k , ans;
vector< PII > from[N] , to[N];


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline void addedge( int u , int v , int w )
{
	to[u].push_back( { v , w } );
	from[v].push_back( { u ,w } );
}

inline void dijkstra()
{
	priority_queue< PII , vector < PII > , greater< PII > > q;
	memset( g , INF , sizeof( g ) );
	g[ed] = 0;
	q.push( { g[ed] , ed } );
	int u , v , dist , w ;
	while( !q.empty() )
	{
		u = q.top().S , dist = q.top().F , q.pop();
		if( vis[u] ) continue;
		for( auto it : from[u] )
		{
			v = it.F , w = it.S;
			if( g[v] <= g[u] + w ) continue;
			g[v] = g[u] + w;
			q.push( { g[v] , v } );
		}
	}
	return ;
}

inline void A_star()
{
	priority_queue< IPII , vector< IPII > , greater< IPII > > q;
	memset( vis , 0 , sizeof( vis ) );
	q.push( { g[st] , { st , 0 } } );
	int u , v , w , dist;
	while( !q.empty() )
	{
		u = q.top().S.F , dist = q.top().S.S , q.pop();

		if( vis[u] >= k ) continue;
		vis[u] ++;

		if( u == ed && vis[u] == k ) printf( "%d\n" , dist ) , exit(0);
		
		for( auto it : to[u] )
		{
			v = it.F , w = it.S;
			if( vis[v] >= k ) continue;
			q.push( { dist + w + g[v] , { v , dist + w } } );
		}
	}
	return ;
}


int main()
{
	n = read() , m = read();
	for( register int i = 1 ; i <= m ; i ++ )
	{
		register int u = read() , v = read() , w = read();
		addedge( u , v , w );
	}
	st = read() , ed = read() , k = read();
	if( st == ed ) k ++;

	dijkstra();

	A_star();

	puts( "-1" );
	return 0;
}

0x28 IDA*

$cdcq$:$ID$还是那个$ID$,$A^*$还是那个$A^*$

首先我们设计一个估价函数，然后在$ID-DFS$的框架下进行搜索

如果当前深度+未来估计深度 > 深度的限制 立即回溯

这就是$IDA^*$的核心，换言之$IDA^*$就是迭代加深的$A^*$

$IDA^*$算法的实现流程基本和$ID - DFS$相同

只需要咋搜索每次执行前写上这句即可

if( dep + f() > max_dep ) return ;

所以$IDA^*$和$A^*$共同精髓都是设计估价函数

并且要保证$f(x)\le f^*(x)$ ,证明如下

红色点是起始状态，绿色点是当前状态，紫色为目标，蓝色线为我们迭代到的最大权值

我们现在要估计绿色到紫色点的权值，如果我么的估计值小于实际值，则已消耗的权值加估计值就一定小于最大权值这可以继续搜索

如果不能保证估计权值小于实际权值，则可能会出现已消耗的权值加估计值大于最大权值，此时就不会继续搜索绿色点的子树，也就不可能的到达紫色点

所以不保证估计值小于实际值就不能保证正确性

AcWing 180. 排书

这道题就是经典的$IDA^*$

由于n比较小，且最多搜索5层，所以可以直接用一个数组来存下每一层的状态

然后就是设计估价函数

我们可以每次修改一个区间

对于任意一种状态下如果$p[i+1] \neq p[i]+1 $则$i$和i+1是一定要调开的，我们把这种情况称作一个错误状态

我们统计一下错误的状态为$cnt$

我们的每一次操作最多可以改变3个错误状态，所以最理想的状态下就是$次可以把整个序列调整成目标序列

所以就得到了一种估价函数$f() = \left \lceil \frac{cnt}{3} \right \rceil$

#include <bits/stdc++.h>
using namespace std;


const int N = 20;
int T , n , q[N] , cur[5][N] , max_dep , ans;
bool flag;

inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
} 

inline int f()
{
	register int cnt = 0;
	for( register int i = 1 ; i < n ; i ++ )
	{
		if( q[ i + 1 ] != q[i] + 1 ) cnt ++ ;
	}
	return (cnt + 2 ) / 3;
}
inline bool check()
{
	for( register int i = 1 ; i <= n ; i ++ ) 
	{
		if( q[i] == i ) continue;
		return 0;
	}
	return 1;
}
inline void ida_star( int dep )
{
	if( dep + f() > max_dep || flag ) return ;
	if( check() )
	{
		ans = dep , flag = 1;
		return ;
	}
	
	for( register int l = 1 ; l <= n ; l ++ )
	{
		for( register int r = l ; r <= n ; r ++ )
		{
			for( register int k = k + 1 ; k <= n ; k ++ )
			{
				memcpy( cur[ dep ] , q , sizeof( q ) );
				register int x , y;
				for( x = r + 1 , y = l ; x <= k ; x ++ , y ++ ) q[y] = cur[dep][x];
				for( x = l ; x <= r ; x ++ , y ++ ) q[y] = cur[dep][x];
				ida_star( dep + 1 );
				if( flag ) return ;
				memcpy( q , cur[dep] , sizeof( q ) );
			}
		}
	}
	
	return ;
}

inline void work()
{
	n = read() , flag = 0;
	for( register int i = 1 ; i <= n ; i ++ ) q[i] = read();
	
	for( max_dep = 1 ; max_dep <= 4 , !flag ; max_dep ++ ) ida_star(0);
	if( flag ) printf( "%d\n" , ans );
	else puts("5 or more");
	return ;
}

int main()
{
	T = read();
	while( T -- ) work();
	return 0;
}

0x31 质数

定义

若一个数，只有一和它本身两个因子，那么这个数就是一个质数

在自然数集中，小于$n$的质数约有$ln(n)$个

试除法

试除法是常用判断素数的方法

inline bool is_prime( int x )
{
	if( x < 2 ) return 0;
	for( register int i = 2 ; i * i <= x ; i ++ )
	{
		if( x % i == 0 ) return 0;
	}
	return 1;
}

素数的筛选

Eratosthenes 筛法（埃拉托色尼筛法）

每次只用素数去筛复杂度$O(nlog_{log_{n}})$

const int N = 1005;
int n,prime[N];

inline void primes()
{
	for(register int i = 2;i <= n;i ++)
    {
    	if(prime[i]) continue;
        for(register int j = 2; i * j <= n; j++) prime[i*j] = 1;
    }
    return ;
}

线性筛（欧拉筛法）

每次只用一个数用小于当前这个数最小质因子的质数去筛其他数，即保证每个数都被自己的最小质因子筛掉

const int N = 10005;
int n,prime[N],cnt;
bool vis[N];

inline void primes()
{
	for(register int i = 2;i <= n;i ++)
    {
    	if(!vis[i]) prime[++cnt] = i;
    	for(register int j = 1;j <= cnt && i * prime[j] <= n; j ++)
        {
        	vis[i * prime[j]] = 1;
            if(i % prime[j] == 0) break;
    	}
    }
}

质因数分解

算数基本定理

任何一个大于1的数都可以被分解成有限个质数乘积的形式

试除法

类似埃式筛，我们直接枚举影子然后把当前因子全部除尽即可

分解成 $p_{1}\times _{2}\times p_{3}\times \cdots \ p_{n}$这种形式

const int N = 1005;
int p[N];

inline int factorize(int x)
{
	register int cnt = 0;
	for(register int i = 2;i * i <= x;i ++)
	{
		while(x % i == 0)
		{
			p[++cnt] = i;
			x /= i;	
		}
	}
	if(x > 1) p[++cnt] = x;
	return cnt;
}

分解成 $p_{1}^{k_{1}} \times p_{2}^{k_{2}} \times p_{3}^{k_{3}} \times \cdots \ p_{n}^{k_{n}}$

const int N = 1005;
int p[N],power[N];


inline int factorize(int x)
{
	register int cnt = 0;
	for(register int i = 2;i *i <= x;i ++)
	{
		if(x%i) continue;
		p[++cnt] = i;
		while(x%i == 0) x /= i,power[cnt] ++;
	}
	if(x == 1) goto end;
	p[++cnt] = x;
	power[cnt] = 1;
	end : return cnt
}

AcWing 196. 质数距离

这道题数据的范围非常的大，我们没有办法在一秒内求出所有质数

但是我们知道一个合数$x$在一定是一个小与$\sqrt{x}$的质数的倍数

所以我们可以求出$(1\cdots \sqrt{U})$的所有质数，然后对于每个区间做埃式筛

然后暴力遍历一遍区间即可

#include <bits/stdc++.h>
#define LL long long

using namespace std;

const int N = 1000010;

int prime[N], cnt , p[N] , tot;
bitset< N > v;

inline void primes()
{
	int n = 50000;
	for( register int i = 2 ; i <= n ; i ++ )
	{
		if( !v[i] ) prime[ ++ cnt ] = i;
		for( register int j = 1 ; j <= cnt && i * prime[j] <= n ; j ++ )
		{
			v[ i * prime[j] ] = 1;
			if( i % prime[j] == 0 ) break;
		}
	}
}


int main()
{
    long long l, r;
    primes();
	while (cin >> l >> r)
    {
		v.reset();
        for (int i = 1; i <= cnt; i ++ )
        {
            int t = prime[i];
            // 把[l, r]中所有t的倍数筛掉
            for (long long j = max((l + t - 1) / t * t, 2ll * t); j <= r; j += t)
                v[j - l] = true;
        }

        tot = 0;
        for (int i = 0; i <= r - l; i ++ )
            if (!v[i] && i + l > 1)
                p[tot ++ ] = i + l;

        if (tot < 2) puts("There are no adjacent primes.");
        else
        {
            int minp = 0, maxp = 0;
            for (int i = 0; i + 1 < tot; i ++ )
            {
                int d = p[i + 1] - p[i];
                if (d < p[minp + 1] - p[minp]) minp = i;
                if (d > p[maxp + 1] - p[maxp]) maxp = i;
            }

            printf("%d,%d are closest, %d,%d are most distant.\n", p[minp], p[minp + 1], p[maxp], p[maxp + 1]);
        }
    }
    return 0;
}

AcWing 197. 阶乘分解

$N!$中质因子$p$的个数等于$1\cdots N$中每个数的质因子$p$的个数之和

包含一个质因子p的数显然都是$p$的倍数，所以有$\left \lfloor \frac{N}{p}\right \rfloor$个质因子

同理包含第二个（不是包含两个）质因子$p$的数显然都是$p^2$的倍数，所以有所以有$\left \lfloor \frac{N}{p^2}\right \rfloor$个质因子，注意不是$2\times\left \lfloor \frac{N}{p^2}\right \rfloor$个，因为第一个已经统计过了

所以$N!$中一共包含$\sum_{k=1}^{p^k\le N}\lfloor\frac{N}{p^k}\rfloor$个质因子

所以我们先求出所有的质因子，再用以上方法求出所有的质因子数即可

#include <bits/stdc++.h>
using namespace std;


const int N = 1000010;
int n , prime[N] , tot;
bool v[N];

inline void primes()
{
	for( register int i = 2 ; i <= n ; i ++ )
	{
		if( !v[i] ) prime[ ++ tot ] = i;
		for( register int j = 1 ; j <= tot && i * prime[j] <= n ; j ++ )
		{
			v[ i * prime[j] ] = 1;
			if( i % prime[j] == 0) break;
		}
	}
	return ;
}


int main()
{
    cin >> n;
    primes();

    for (int i = 1; i <= tot; i ++ )
    {
        register int p = prime[i] , cnt = 0;
        for ( p ; p <= n ; p *= prime[i] )
        {
            cnt += n / p;
            if( p > n / prime[i] ) break;
            //等价于 if( p * prime[i] > n ) break; 防止溢出
        }
        cout << prime[i] << ' ' << cnt << endl;
    }

    return 0;
}

0x32 约数

定义

若整数$n$除以整数$x$的余数为$0$，即$d$能整除$n$，则称$d$是$n$的约数，$n$是$d$的倍数，记为$d|n$

算术基本定理推论

由算数基本定理得正整数N可以写作$N=p_1^{C_1}\times p_2^{C_2} \times p_3^{C_3} \cdots \times p_m^{C_m}$

N的正约数个数为($\Pi$是连乘积的符号，类似$\sum$)

\[(c_1+1)\times (c_2+1)\times \cdots (c_m+1)=\Pi_{i=1}^{m}(ci+1) \]

$N$的所有正约数和为

\[(1+p_1+p_1^2+\cdots +p_1^{c_1})\times\cdots\times(1+p_m+p_m^2+\cdots +p_m^{c_m})=\prod_{i=1}^{m}(\sum_{j=0}^{c_i}(p_i)^j) \]

求$N$的正约数的集合

对于任意的$d|n$则$(\frac{n}{d})|n$

所以只要扫描$1\cdots\sqrt n$就能找到n的所有正约数，复杂度$O(\sqrt n)$

int factor[N] , tot = 0;
for( int i = 1 ; i * i <= n ; i ++ )
{
	if( n % i ) continue;
	factor[ ++ tot] = i;
	if( i != n / i ) factor[ ++ tot ] = n / i;
}

AcWing 198. 反素数

引理1

$1\cdots N$中最大的反素数就是约数个数最多的数中最小的一个

证明：

设$m$是$1\cdots N$中约数个数最多的数中最小的一个。根据$m$的定义，$m$满足

$\forall x < m ,g(x)\le g(m) $
$\forall x>m,g(x) \le m$

第一条性质说明$m$是反素数，第二条性质说明大于$m$的都不是反素数

引理2

$1\cdots N$中任何数的不同质因子都不超过$10$个，任何质因子的指数总和不超过$30$

证明：

最小的$11$个质因子乘积$2\times3\times5\times7\times11\times13\times17\times19\times23\times29\times31>2\times10^9$

最小的质数的$31$次方$2^{31}>2\times10^9$

引理3

$\forall x \in [1,N]$，x为反素数的必要条件是：

x分解质因数后可写作$2^{c_1}\times3^{c_3}\times5^{c_3}\times7^{c_4}\times11^{c_5}\times13^{c_6}\times17^{c_7}\times19^{c_8}\times23^{c_9}\times29^{c_{10}}$

并且$c_{1}\geq c_{2}\geq c_{3}\geq c_{4}\geq c_{5}\geq c_{6}\geq c_{7}\geq c_{8}\geq c_{9}\geq c_{10}\geq0 $

证明：

反正法，由引理$2$，$x$的质因数分解式中存在一项$p^k(p>29)$，则必定有一个不超过29的质因子${p}’$不能整除$x$。根据算数基本定理的推论，$\frac{x}{p^k}\times{p}'^k$的约数个数与$x$的约数个数相等，但前者更小，所以，这与反质数的定义矛盾。故$x$只包含$29$以内的质因子

同理，若$x$的质因子不是连续若干最小的，或者质数不单调递减，我们可以通过上述交换质因子的方法，的到一个比$x$更小的、但约数个数相同的整数。因此假设不成立，原命题成立

综上所述，我们可以用$DFS$确定前十个质数的指数，并满足指数单调递减，总乘积不超过N，同时记录约数个数

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 2e9+5 , t = 10 , p[t] = { 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 21 , 29 };
int n , sum = 0 , minx;


inline void dfs( int u , int last , int pi , int s )
{
	if( s > sum || s == sum && pi < minx ) sum = s , minx = pi;
	for( register int i = 1 ; i <= last ; i ++ )
	{
		if( (LL)pi * p[u] > n ) break;
		pi *= p[u];
		dfs( u + 1 , i , pi , s * ( i + 1 ) );
	}
	return ;
}


int main()
{
	cin >> n;
	dfs( 0 , 30 , 1 , 1 ); 
	cout << minx << endl;
}

AcWing 199. 余数之和

首先注意到$k \mod i = k- \left \lfloor \frac{k}{x} \right \rfloor$,故可以转化为$n\times k - \sum_{i=1}^{n}\left \lfloor \frac{k}{i} \right \rfloor\times i$

对于任意的$x\in[1,k]$，设$g(x)= \left \lfloor k/ \left \lfloor \frac{k}{x}\right \rfloor \right \rfloor$

因为

\[\left\lfloor\frac{k}{x} \right\rfloor \le \frac{k}{x}\Rightarrow g(x)\ge \left\lfloor \frac{k}{k /x}\right\rfloor = x \]

所以可得

\[\left\lfloor\frac{k}{g(x)}\right\rfloor\le\left\lfloor\frac{k}{x}\right\rfloor \]

又因为

\[g(x)\le\frac{k}{\lfloor k/x \rfloor}\Rightarrow\left\lfloor \frac{k}{g(x)}\right\rfloor\ge\left\lfloor \frac{k}{k/\lfloor\frac{k}{x}\rfloor}\right\rfloor = \left\lfloor \frac{k}{x}\right\rfloor \]

所以可得

\[\left\lfloor \frac{k}{g(x)}\right\rfloor=\left\lfloor \frac{k}{x}\right\rfloor \]

所以可知$\forall i \in[x,g(x)]$，$\lfloor \frac{k}{i}\rfloor$恒为定值

所以在区间[x,g(x)]中$k\mod i$的值是个等差数列，利用高斯公式$O(1)$求和

对于$\forall x\in[1,n]$ ，$\left\lfloor \frac{k}{x}\right\rfloor$只有$2\sqrt{n}$中结果，相当于把$[1,n]$分成了$2\sqrt{n}$段，每段$\left\lfloor \frac{k}{x}\right\rfloor$都相同

每一段的余数和可以直接用公式求得，所以最终的复杂度就是$O(\sqrt{n})$

int main()
{
	long long n , k , ans;
	cin >> n >> k;
	ans = n * k;
	for( register int x = 1 , gx ; x <= n ; x = gx + 1 )
	{
		gx = ( k / x ) ? min( k / ( k / x ) , n ) : n;
		ans -= (k/x) * ( x + gx ) * ( gx - x + 1 ) / 2;
	}
	cout << ans << endl;
	return 0;
}

最大公约数

定义

若自然数$d$同时是$a$和$b$的约数，则称$d$是$a$和$b$的公约数

在所有的公约数中最大的一个就是最大公约数，记作$gcd(a,b)$

若自然数$m$同时是$a$和$b$的倍数，则成$m$是$a$和$b$的公约数

在所有的公倍数中最小的一个就是最小公倍数，记住$lcm(a,b)$

同理，我们也可以定义三个数以及更多数的最大公约数或最小公倍数

定理

\[\forall a,b \in N,gcd(a,b)\times lcm(a,b)=a\times b \]

证明：

设$d=gcd(a,b),a_0=\frac{a}{d},b_0=\frac{b}{d}$

根据定义得$gcd(a_0,b_0)=1,lcm(a_0,b_0)=a_o\times b_0$

所以$lcm(a,b)=lcm(a_0\times d,b_0\times d)=lcm(a_0,b_0)\times d=a_0\times b_0 \times d = \frac{a \times b }{d} $

更相减损术

\[\forall a,b \in N , a > b,有gcd(a,b)=gcd(b,a-b)=gcd(a,a-b) \\ \forall a,b \in N , 有gcd(2a,2b) = 2gcd(a,b) \]

证明

根据最大公约数的定义，后者显然成立，我们主要证明前者

对于任意的公约数$d$，因为$d|a,d|b$,所以$d|(a-b)$因此d也是$b,a-b$的公约数

反之亦然成立，故$a,b$的公约数集合与$b,a-b$的公约数集合相同

欧几里得算法

\[\forall a , b \in N , b \ne 0, gcd(a,b) = gcd(b , a \mod b) \]

原理其实和更相减损术是一样的，做多次减法直到减不下实际上就等价于做一次取摸

inline int gcd( int a , int b ) { return b ? gcd( b , a % b ) : a; }

欧几里得算法是常用的求最小公倍数的算法，但是如果遇到需要取模和高精度的时候，考虑到高精度实现取模运算比较复杂，可以考虑用更相减损术来代替欧几里得，并且时间复杂度是相同的

Luogu P1072 Hankson 的趣味题

为了方便叙述我们把$a_0,a_1,b_0,b_1$重新定义为$a,b,c,d$

首先可以最小公倍数的定义可知$x|d$

所以我们可以直接枚举$d$的因子即可

对于最小公倍数的判断可以进行一些变形

\[\because lcm(a,b)\times gcd(a,b)=a\times b\\ \therefore lcm(x,c)=d\Leftrightarrow d\times gcd(x,c)= x \times c \]

int main()
{
	T = read();
	while( T -- )
	{
		a = read() , b = read() , c = read() , d = read() , ans = 0;
		for( register int i = 1 , j ; i * i <= d ; i ++ )
		{
			if( d % i ) continue;
			if( gcd( i , a ) == b && d * gcd( i , c ) == i * c ) ans ++;
			j = d / i;
			if( gcd( j , a ) == b && d * gcd( j , c ) == j * c ) ans ++;
		}
		printf( "%d\n" , ans );
	}
	
	return 0;
}

互质与欧拉函数

定义

\[\forall a,b\in N 若gcd(a,b)=1,则称a,b互质 \]

对于三个数或更多的数，$gcd(a,b,c)=1 \Leftrightarrow gcd(a,b) = gcd(a,c)=gcd(b,c)=1$

欧拉函数

$1\cdots N$中与N互质的数的个数，被称为欧拉函数，记作$\phi(N)$

由算数基本定理得$N= p_{1}^{k_{1}} \times p_{2}^{k_{2}} \times p_{3}^{k_{3}} \times \cdots \ p_{m}^{k_{m}}$

所以$\phi(N) = N \times \frac{p_1-1}{p_1}\times \frac{p_2-1}{p_2}\times \cdots \times \frac{p_m-1}{p_m} = N \times \Pi_{p|N}(1-\frac{1}{p})$

证明

假设$N$有两个质因子$p,q$

在$1\cdots N$中$p$的倍数有$\frac{N}{p}$个，同理$q$的倍数也有$\frac{N}{q}$个

我们把$\frac{N}{p}$和$\frac{N}{q}$排除掉，显然$p\times q$ 的倍数被排除了两次所以要加上$\frac{N}{p\times q}$

\[\phi(N) = N - \frac{N}{p}-\frac{N}{q}+\frac{N}{p\times q} = N\times(1-\frac{1}{p}-\frac{1}{q}+\frac{1}{p\times q}) = N\times(1-\frac{1}{p})\times(1-\frac{1}{q}) \]

根据数学归纳法可以把上诉结论扩展至任意个质因子

所以我们可以在做质因数的同时，求出欧拉函数

inline int phi( int x )
{
	register int ans = x;
	for( register int i = 2 ; i * i <= x ; i ++ )
	{
		if( x % i ) continue;
		ans = ans / i *( i - 1 );
		while( x % i == 0 ) n /= i;
	}
	if( n > 1 ) ans = ans  / n *  ( n - 1 );
	return ans ;
}

性质1~2

$\forall n > 1 , 1\cdots n中与互质的数的和为n\times \phi(n) / 2 $
若a,b互质，则$\phi(ab)=\phi(a)\phi(b)$

积性函数

如果当a,b互质时，满足$f(ab)=f(a)f(b)$的函数$f$称为积性函数

性质3~6

若f是积性函数，且在算数基本定理中$n=\Pi_{i=1}^{m} p_i^{c_i}$，则$f(n) = \Pi_{i=1}^{m} f(p_i^{c_i})$
设$p$为质数，若$p|n$且$p^2|n$ , 则$\phi(n) = \phi( \frac{n}{p})\times p$
设$p$为质数，若$p|n$且$p^2 \not|n$,则$\phi(n) = \phi(\frac{p}{n})\times (p-1)$
$\sum_{d|n}\phi(d)=n$

性质4~6，只适用于欧拉函数，并非所有的积性函数都适用

$O(n)$递推求欧拉函数

const int N = 1e3+5;
int prime[N] , phi[N] , tot ;
bool v[N];

for( register int i = 2 ; i <= n ; i ++ )
{
	if( !v[i] ) prime[ ++ tot ] = i , phi[i] = i - 1;
	for( register int j = 1 ; j <= tot && i * prime[j] <= n ; j ++ ) 
	{
		v[ i * prime[j] ] = 1;
		phi[ i * prime[j] ] = phi[i] * ( i % prime[j] ? prime[j] - 1 : prime[j] );
        if( i % prime[j] == 0 ) break; 
	}	
}

根据性质4、性质5得

补充证明

若$i|p_j$ ，则$i=k\times p_j$

所以$n=i\times p_j = k\times p_j^2$

故$p_j|n$,且$p_j^2|n$

[SDOI2008]仪仗队

JZYZOJ P1377

AcWing 201. 可见的点和本题基本相同，不单独讲

首先我们将原图从$(1,1)$到$(n,n)$重新标号$(0,0)$到$(n-1，n-1)$

分析题目可知，当$n=1$时，显然答案是$0$，特判断即可

我们考虑 $n \ne1$的情况，首先$(0,1),(1,0),(1,1)$这三个点是一定能看到的

考虑剩余的点

对于任意的点$(x,y)，2\le x,y\le n-1$，若不被其它的点挡住必定满足$gcd(x,y) = 1$

证明

若点$(x,y)$ 不满足$gcd(x,y)=1$，令$d = gcd(x,y)$

则$(x,y)$与$(0,0)$连线的斜率$k=\frac{y}{x} = \frac{y/d}{x/d}$

所以$(x,y)$会被$(x/d,y/d)$挡住

然后我们把这个图按照对角线分成两个等腰直角三角形

若点$(x,y)$在一个三角形中，并满足$gcd(x,y)=1$

则必有一个点$(y,x)$在另一个三角形中,并满足$gcd(y,x) = 1$

所以只统计其中一个三角形即可

现在我们在$y<x$的三角形中考虑

对于任意一个$x$,满足条件的$y$的个数就是$\phi(x)$

所以答案就是

\[3+2\times\sum_{i=2}^{n-1}\phi(i) \]

所以们$O(n)$的地推欧拉函数的同时求和即可

#include <bits/stdc++.h>
using namespace std;

const int N = 40005;
 
int n , sum , prime[N] , phi[N] , tot ;
bool v[N];

int main()
{
	cin >> n;
	if( n == 1 ) puts("0") , exit(0);
	n --;
	for( register int i = 2 ; i<= n ; i ++ )
	{
		if( !v[i] ) prime[ ++ tot ] = i , phi[i] = i - 1;
		sum += phi[i]; 
		for( register int  j = 1 ; j <= tot && i * prime[j] <= n ; j ++ )
		{
			v[ i * prime[j] ] = 1;
			phi[ i * prime[j] ] = phi[i] * ( i % prime[j] ? prime[j] - 1 : prime[j] );
            if( i % prime[j] == 0 ) break;
		}
	} 
	cout << sum * 2 + 3 << endl;
}

0x33同余

定义

若正整数$a$和$b$除以$m$的余数相等，则称$a$，$b$模$m$同余，记作$a \equiv b(mod \ m)$

性质

自反性：$a\equiv a (mod \ m)$
对称性：若$a\equiv b(mod \ m)$，则$b \equiv a (mod\ m)$
传递性：若$a \equiv b(mod\ m) , b\equiv c(mod\ m)$，则$a\equiv c(mod\ m)$
同加性：若$a\equiv b(mod\ m)$，则$a+c\equiv b+c(mod\ m)$
同乘性：若$a\equiv b(mod\ m)$，则$a\times c \equiv b\times c(mod\ m)$，若$a\equiv b(mod\ m) , c\equiv d (mod\ m)$，则$a\times c \equiv b\times d (mod\ m)$
同幂性：若$a\equiv b(mod\ m)$，则$a^c\equiv b^c(mod\ m)$
$a\times b\%\ k=(a\%k)\times(b\%k)\%k$
若$a\%p=x,a\%q=x,gcd(p,q)=1$，则$a\%(p\times q) = x$
不满足同除，若$a\equiv b(mod\ m)$不满足$a\div c\equiv b\div c(mod\ m)$

费马小定理

若$p$是质数，则对于任意正整数$a$都有 $a^p\equiv a(mod\ p)$或$a^{p-1}\equiv 1(mod\ p)$

欧拉定理

若正整数$a,n$互质，则$a^{\phi(n)}\equiv 1(mod\ n)$其中$\phi(n)$是欧拉函数

费马小定理是欧拉定理的一种特殊情况

欧拉定理推论

若正整数$a,n$互质，则对于任意的正整数$b$，有$a^b\equiv a^{b\ mod \ \phi(n)}(mod \ n)$

在一些计数的问题中，常常要求对结果取模，但面对乘方时，无法直接取模，可以先把底数对$p$取模，指数对$\phi(p)$取模，再计算乘方

特别的，当不保证$a,n$互质时，若$b>\phi(n)$，有$a^b\equiv a^{b\ mod \ \phi(n)+\phi(n)}(mod \ n)$

这也就意味着即使不保证互质，我们也可把乘方运算缩小到容易计算的规模

AcWing 202. 最幸运的数字

$x$个8连在一起组成的整数可写作$8(10^x-1)/9$，题目就是要求我们求最小的$x$满足$L|8(10^x-1)/9$

设$d = gcd(L,8)$

\[L|\frac{8(10^x-1)}{9}\Leftrightarrow 9L|8(10^x-1)\Leftrightarrow \frac{9L}{d}|10^x-1\Leftrightarrow 10^x\equiv1(mod\ \frac{9L}{d}) \]

引理：

若正整数$a,n$互质，则满足$a^x\equiv 1(mod n)$的最小正整数$x_0$是$\phi(n)$的约数

证明

反证法：假设满足$a^x\equiv 1(mod n)$的最小正整数$x_0$不是$\phi(n)$的约数

设$\phi(n)=qx_0+r,(0<r<x_0)$，因为$a^{x_0}\equiv1(mod\ n)$，所以$a^{qx_0}\equiv 1(mod\ n)$

又因欧拉定理得$a^{\phi(n)} \equiv 1(mod\ n)$，所以可得$a^{r}\equiv 1(mod \ n)$

假设不成立，所以假设错误

证毕

根据以上定理，我们只需求出$\phi(\frac{9L}{d})$,枚举他所有的约数，用快速幂逐一检查条件即可

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const LL INF = 1e18;
LL l, mod , ret , p ;

inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' ) x = ( x << 3 ) + ( x << 1 ) + ch - '0' , ch = getchar();
	return x;
}

inline int gcd( int a , int b ) { return b ? gcd( b , a % b ) : a ; }

inline LL power(LL x , LL  p )
{
	register LL ans = 1;
	while( p )
	{
		if( p & 1 ) ans = ( ans * x ) % mod;
		x = ( x * x ) % mod;
		p >>= 1; 
	}
	return ans;
}

inline int phi( int x )
{
	register int ans = x;
	for( register int i = 2 ; i * i <= x ; i ++ )
	{
		if( x % i ) continue;
		ans = ans / i * ( i - 1 );
		while( x % i == 0 ) x /= i;
	}
	if( x > 1 ) ans = ans / x * ( x - 1 );
	return ans;
}

inline void work()
{
	mod = l / gcd( 8 , l ) * 9 , p = phi( mod ) ,ret = INF;
	for( register LL i = 1 ; i * i <= p ; i ++)
	{
		if( p % i ) continue;
		if( power( 10 , i  ) ==  1 ) ret = min( ret , i );
		if( power( 10 , p / i ) == 1 )  ret = min( ret , p / i ); 
	}
	return ;
}

int main()
{
	for( register int i = 1 ; i ; i ++  )  
	{
		l = read();
		if( l == 0 ) break;
		work() , printf( "Case %d: %d\n" , i , (ret == INF ? 0 : ret ) );
	} 
	return 0;
}

裴蜀定理

对于任意的$a$,$b$存在无穷多组整数对$(x,y)$满足不定方程$ax+by=d$,其中$d=gcd(a,b)$

$ax+by=d \ (d=gcd(a,b))$这个方程叫丢番图方程

扩展欧几里得算法

在求$gcd(a,b)$的同时，可以求出关于$x,y$的不定方程$ax+by=d$的一组解

考虑递归计算：假设已经算出了$(b\%a,a)$的一组解$(x_{0} , y_{0})$满足$(b\%a)x_0+ay_0=d$

可以得到$(b-a\lfloor \frac{b}{a} \rfloor)x_0+ay_0 = d$

整理得到$a(y_0 - \lfloor \frac{b}{a} \rfloor x_0) + bx_0 = d$

为了方便表示$swap(x_0,y_0)$得$a(x_0 - \lfloor \frac{b}{a} \rfloor y_0) + by_0 = d$

就可以得到一组解$((x_0 - \lfloor \frac{b}{a} \rfloor y_0),y_0)$

inline int exgcd(int a,int b,int &x,int &y)
{
	if(a == 0)
	{
		x  = 0,y = 1;
		return b;
	}
	int d = exgcd(b%a,a,y,x);
	x -= b / a * y;
	return d;
}

扩展欧几里得一元线性同余方程

解关于$x$的一元线性同余方程$ax\equiv b(mod\ m)$

已知扩展欧几里得可以解$ax_0+by_0=d,(d = gcd(a,m))$

将原方程变形得$ax + my = b$

通过扩展欧几里得可解出$ax^\prime + my^\prime = d$

当$b\%d==0$时$ax + my = b$有解,反之无解

方程$ax^\prime + my^\prime = d$两边同乘$\frac{b}{d}$得$a\frac{b}{d}x^\prime+m\frac{b}{d}y^\prime = b$

我们就把原方程解出来$x = \frac{b}{d}x^\prime$

乘法逆元

在之前我们提到过，除法不能直接取模，但是可以用逆元

若$x$满足$ax\equiv 1(mod \ n )$，则称$x$是$a$在模$n$意义下的逆元记作$a^{-1}$

当然满足条件的逆元不止一个，通常情况下我们只用最小正整数的逆元，并且逆元也不在任何条件下都有逆元

求逆元

下面介绍三种最常用的求逆元的方法

费马小定理

费马小定理 $a^{p-1} \equiv 1(mod\ p)$,其中$p$为素数

根据费马小定理变形得$aa^{p-2}\equiv 1(mod\ p)$

则$a^{p-2}\% p$就是逆元，直接快速幂求得

inline int invers(int x,int p)
{
	return ksm(x,mod-2,p) % p;
}

扩展欧几里得

根据逆元的定义$ax \equiv 1(mod\ m)$得$ax+my=1$

解这个丢番图方程可得$x\%m$就是逆元，同时可得逆元存在的条件$gcd(a,m) = 1$

inline int invers(int a,int mod)
{
	register int x,y;
	exgcd(a,mod,x,y);
    return (x % mod + mod) % mod;
}

线性递推

$a^{-1} =\displaystyle -\left \lfloor \frac{m}{a}\right\rfloor\times(m\%a)^{-1}$

const int N = 1005;
int inv[N] = {};

inline void invers(int n,int mod)
{
	inv[1] = 1;
    for(register int i = 2;i <= n;i ++)
			inv = (long long)(mod - mod / i) * inv[mod % i] % mod;
	return ;
}

线性同余方程

给定整数$a,b,m$，求一个整数$x$满足$a\times x\equiv b(mod \ m)$，或者无解。因为未知数的指数为一，所以成为一次同余方程或线性同余方程

解关于$x$的一元线性同余方程$ax\equiv b(mod\ m)$

已知扩展欧几里得可以解$ax_0+by_0=d,(d = gcd(a,m))$

将原方程变形得$ax + my = b$

通过扩展欧几里得可解出$ax^\prime + my^\prime = d$

当$b\%d==0$时$ax + my = b$有解,反之无解

方程$ax^\prime + my^\prime = d$两边同乘$\frac{b}{d}$得$a\frac{b}{d}x^\prime+m\frac{b}{d}y^\prime = b$

我们就把原方程解出来$x = \frac{b}{d}x^\prime$

中国剩余定理CRT

又称中国余数定理或孙子定理，最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

简单来说就求一元线性同余方程组
$\left\{\begin{matrix} x \equiv a_1(mod\ m_1)\\x \equiv a_2(mod\ m_2)\\\vdots\\x \equiv a_n(mod\ m_n) \end{matrix}\right.$

对于这样的一个方程组如果任意的两个$m$都互素，则一定有解
所以中国剩余定理就是解但$m$互素的情况

我们尝试来构造这样一组解

设$M = m_1 \times m_2 \times \cdots \times m_n,M_i = \frac{M}{m_i}$

$M_i$只有在模$m_i$时不为零，模其他$m$都是零

由于我们希望在模$m_i$时得到$a_i$所以乘上$a_it_i$

其中$t_i$是$M_i$在模$m_i$时的逆元

所以最小正整数解就是$x = \sum_{i=1}^{n}a_it_iM_i$，通解就是$x+kM$

如果题目说明了的$m$都是素数则可以用费马小定理

inline int crt()
{
	register int ans = 0,M = 1;
	for(register int i = 1;i <= n;i ++) M *= m[i];
	
	for(register int i = 1;i <= n;i ++)
	{
		register int Mi = M/m[i],invers = ksm(Mi,m[i]-2,m[i]);
		ans = (ans + a[i]*invers*Mi) % M;
	}
	return ans;
}

如果题目没有说明我们还是用扩展欧几里得来求逆元

inline int crt()
{
	register int M = 1, ans = 0;
	for(register int i = 1;i <= n; i ++) M *= m[i];
	for(register int i = 1;i <= n; i ++)
	{
		register LL Mi = M/m[i],x,y;
		exgcd(Mi,m[i],x,y);
		ans = ((ans + a[i] * Mi * x) % M + M) % M;
	}
	return ans;
}

证明中国剩余定理一定有解

我们举这个同余方程为例

$\left\{\begin{matrix} x \equiv a_1(mod\ m_1)\\x \equiv a_2(mod\ m_2)\\ \end{matrix}\right.$

假设我们分别解出

$\left\{ \begin{matrix} x_1 = a_1+k_1 \times m_1 \\ x_2 = a_2 + k_2 \times m_2 \end{matrix}\right.$

因为 $x_1 = x_2$

所以$a_1+k_1\times m_1 = a_2 + k_2 \times m_2$

整理得$k_2\times m_2 - k_1\times m_1 = a_1-a_2$

这就是$ax+by=d$的形式

所以当$gcd(m_1,m_2)|a_1-a_2$ 时一定有解

又因为$m_1$与$m_2$互质

所以$gcd(m_1,m_2) = 1$

显然中国剩余定理一定有解

扩展中国剩余定理EXCRT

扩展中国剩余定理就是解一元线性同余方程组

$\left\{\begin{matrix} x \equiv a_1(mod\ m_1)\\x \equiv a_2(mod\ m_2)\\\vdots\\x \equiv a_n(mod\ m_n) \end{matrix}\right.$

但是这里的$m$不要求互素，这是与中国剩余定理不同的地方

假设们我已经求出前$k-1$个等式的最小整数解$x$

令$M = LCM(m_1,m_2,\cdots,m_{k-1})$

则前$k-1$个等式的通解为$x+tM\ (t\in Z)$

我们要找$x+t^\prime M \equiv a_k (mod\ m_k)$

新的解$x^\prime = x + t^\prime M$

所以解$n$个方程就可以求出最后的解

怎么解$x+t^\prime M \equiv a_k (mod\ m_k)$呢?

我们可以化成$t^\prime M \equiv a_k - x(mod\ m_k)$

我们可以用扩展欧几里得解出$t^\prime$,这样我们就构造出呢前$k$个方程的一组特解

inline int excrt()
{
	register int x = a[1],M = m[1],t,y,c,d,mod; 
	for(register int i = 2;i <= n;i ++)
	{
		c = ((a[i] - x) % m[i] + m[i]) % m[i]; d = exgcd(M,m[i],t,y);
		if(c%d) return -1;
		mod = m[i] / d;
		t = ((t * (c/d)) % mod + mod) % mod;
		x += t * M;
		M *= mod;
		x = (x + M) % M;
	}
	return x;
}

对于第一个方程$x=a_1 , M= m_1$
$c = a_i - x$
$x \% \frac{M\times m_i}{d} = (x\%\frac{m_i}{d})\%M$ 所以$mod = \frac{m_i}{d}$

Luogu P1082 同余方程

非常非常落的模板题，记得用long long

#define LL long long

int main()
{
	LL a , b ;
	cin >> a >> b;
	LL x , y;
	exgcd( a , b , x , y );
	cout << ( x % b + b ) % b << endl;
	return 0;
}

Luogu P4777 扩展中国剩余定理

本题有弱化版AcWing 204. 表达整数的奇怪方式

非常裸的$excrt$，记住用快速乘

0x34 矩阵乘法

矩阵

数学上，一个$n\times m$的矩阵是一个有$m$行$n$列的元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。一下是一个由$6$个元素构成的$2$行$3$列的矩阵

\[\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{bmatrix} \]

大小相同（行列数都相同）的矩阵可以相加减，具体做法是每个对应位置上的元素相加减

特殊的矩阵

方阵

如果一个行数和列数都相同的矩阵，我们称作方阵，下面是一个$3\times3$的方阵

\[\begin{bmatrix}1 & 2 & 3\\4&5&6\\7&8&9\end{bmatrix} \]

单位矩阵

对于$n\times n$的方阵，如果主对角线上的元素为$1$，其余元素全为$0$我们称为$n$阶单位矩阵，一般用$In$或$En$表示，通常情况下简称$I$或$N$，下面是一个$4$阶单位矩阵

\[\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} \]

主对角线：从左上到右下的对角线

反对角线：从右上到左下的对角线

矩阵乘法

详细的矩阵乘法的运算过程可以参考这个视频

\[\begin{bmatrix} 3 & 1 & -1\\ 2 & 0 & 3 \end{bmatrix} \times \begin{bmatrix} 1&6\\ 3&-5\\ -2&4\\ \end{bmatrix} = \begin{bmatrix} 3\times 1+1\times3+(-1)\times(-2)&2\times1+0\times3+3\times(-2)\\ 3\times6+1\times(-5)+(-1)\times4&2\times6+0\times(-5)+3\times4 \end{bmatrix} =\begin{bmatrix} 8&9\\-4&24\end{bmatrix} \]

定义

设$A$是$n\times m$的矩阵$B$是$m\times p$ 的矩阵，则$C=A\times B$是$n\times p$的矩，并且

\[\forall i\in [1,n], \forall j\in[1,p]：c_{i,j}=\sum_{k=1}^{m}A_{i,k}\times B_{k,j} \]

也就是说，参与矩阵乘法的矩阵第一个矩阵的列数必须等于第二个矩阵的行数，否则不能运算

矩阵乘法满足结合律$(A\times b)\times C = A \times (B \times C)$，满足分配律$(A+B)\times C = A\times C + B \times C $，但不满足交换律$A\times B \ne B \times A$

方阵乘幂

方阵乘幂是指，$A$是一个方阵，将$A$连乘$n$次，即$C = A^n$

若不是方阵则不能进行方阵乘幂

由于矩阵乘法满足结合律，所以可以用快速幂的实现来实现矩阵快速幂

矩阵乘法的应用

矩阵乘法奥妙在于：

很容易将有用的状态储存在一个矩阵中
通过状态矩阵和状态转移矩阵相乘快速的得到一次$DP$的值（这个$DP$的状态转移方程必须是一次的）
求矩阵乘法的结果是要做很多次乘法，这样的效率非常慢甚至比不上直接递推进行$DP$的状态转移，但由于矩阵乘法满足结合律，可以先算后面的转移矩阵，即用快速幂，迅速的处理好后面的转移矩阵，再用初始矩阵乘上后面的转移矩阵得到结果，复杂度是$O( log(n) ) $的

Loj 10219.矩阵 A×B

矩阵乘法的模板题

const int N = 105;
int n , m , q , a[N][N] , b[N][N] , c[N][N];

int main()
{
	n = read() , m = read();
	for( register int i = 1 ; i <= n ; i ++ )
	{
		for( register int j = 1 ; j <= m ; j ++ ) a[i][j] = read();
	}
	q = read();
	for( register int i = 1 ; i <= m ; i ++ )
	{
		for( register int j = 1 ; j <= q ; j ++ ) b[i][j] = read();
	}
    //代码的核心矩阵乘法
	for( register int i = 1 ; i <= n ; i ++ )
	{
		for( register int j = 1 ; j <= q ; j ++ )
		{
			for( register int k = 1 ; k <= m ; k ++ ) c[i][j] += a[i][k] * b[k][j];
		}
	}
	for( register int i = 1 ; i <= n ; i ++ )
	{
		for( register int j = 1 ; j <= q ; j ++ ) printf( "%d " , c[i][j] );
		puts("");
	}
	return 0;
}

Loj 10220.Fibonacci 第 n 项

本题看似简单，但巨大的数据范围开数组肯定开不下，并且线性求解效率也很低

我们知道

\[f[i]=1\times f[i-1] + 1\times f[i-2]\ (1)\\ f[i-1] = 1\times f[i - 1]+0\times f[i-2]\ (2) \]

观察上面两个式子，我们可以把他改写成矩阵乘法的形式

\[\begin{bmatrix}f[i]\\f[i-1]\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}\times\begin{bmatrix}f[i-1]\\f[i-2]\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}\times \begin{bmatrix}1&1\\1&0\end{bmatrix}\times\begin{bmatrix}f[i-2]\\f[i-3]\end{bmatrix} \]

根据数学归纳法们就能得到

\[\begin{bmatrix}f[n]\\f[n-1]\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix}^{n-2}\times\begin{bmatrix}f[2]\\f[1]\end{bmatrix} \]

之前我们提到过矩阵可以快速幂，所以我们就可以在$O(log(n))$的复杂度内求出$f[n]$

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 5;
LL n , m ;

struct matrix
{
	int x , y ;
	LL v[N][N];
	inline friend matrix operator * ( matrix a , matrix b )
	{
		register matrix cur;
		cur.x = a.x , cur.y = b.y;
		for( register int i = 1 ; i <= a.x ; i ++ )
		{
			for( register int j = 1 ; j <= b.y ; j ++ )
			{
				cur.v[i][j] = 0;
				for( register int k = 1 ; k <= a.y ; k ++ )
				{
					cur.v[i][j] += a.v[i][k] * b.v[k][j];
					cur.v[i][j] %= m; 
				}
			}
		}
		return cur;
	}
}f , res , cus ;


inline void matrix_I( matrix & k , int t )
{
	k.x = k.y = t;
	for( register int i = 1 ; i <= t ; i ++ )
	{
		for( register int j = 1 ; j <= t ; j ++ )
		{
			if( i == j ) k.v[i][j] = 1;
			else k.v[i][j] = 0;
		}
	}
	return ;
}

inline matrix matrix_power( matrix x , int k )
{
	register matrix t; matrix_I( t , 2 );
	while( k )
	{
		if( k & 1 ) t = t * x;
		x = x * x;
		k >>= 1;
	}
	return t ;
}

inline LL fib()
{
	if( n <= 2 ) return 1;
	f.x = f.y = 2;
	f.v[1][1] = f.v[1][2] = f.v[2][1] = 1 , f.v[2][2] = 0;
	res.x = 2 , res.y = 1;
	res.v[1][1] = res.v[2][1] = 1;
	f = matrix_power( f , n - 2 );
	res = f * res;
	return res.v[1][1] ;
}


int main()
{
	cin >> n >> m;
	cout << fib() << endl;
	return 0;
}

Loj 10221.Fibonacci 前 n 项和

本题在上一题的基础上增加了求和，我们依旧要构造状态转移矩阵

\[s[n] = 1 \times s[n-1] + 1 \times f[n] + 0 \times f[n-1]\\ f[n+1] = 0 \times s[n-1] + 1 \times f[n] + 1 \times f[n-1]\\ f[n] = 0 \times s[n-1] + 1 \times f[n] + 0 \times f[n-1] \]

所以我么可以根据上面的三个式子推出状态转移矩阵

\[\begin{bmatrix} s[n] \\ f[n+1] \\ f[n] \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} s[n-1] \\ f[n] \\ f[n-1] \end{bmatrix} \]

然后就依旧是矩阵快速幂

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N  = 5;
int n , m ;

struct matrix
{
	LL v[N][N];
	int x , y;
	inline friend matrix operator * ( matrix a , matrix b )
	{
		register matrix cur;
		cur.x = a.x , cur.y = b.y;
		for( register int i = 1 ; i <= cur.x ; i ++ )
		{
			for( register int j = 1 ; j <= cur.y ; j ++ )
			{
				cur.v[i][j] = 0;
				for( register int k = 1 ; k <= a.y ; k ++ ) cur.v[i][j] = ( cur.v[i][j] + a.v[i][k] * b.v[k][j] ) % m;
			}
		}
		return cur;
	}
} res , f;


inline void matrix_I( matrix & k , int t )
{
	k.x = k.y = t;
	for( register int i = 1 ; i <= t ; i ++ )
	{
		for( register int j = 1 ; j <= t ; j ++ ) k.v[i][j] = ( i == j ) ? 1 : 0;
	}
	return ;
}

inline matrix matrix_power( matrix x , int k )
{
	register matrix t ; matrix_I( t , 3 );
	while( k )
	{
		if( k & 1 ) t = t * x;
		x = x * x;
		k >>= 1;
	}
	return t;
}

inline LL fib()
{
	if( n == 1 ) return 1;
	if( n == 2 ) return 2;
	f.x = f.y = res.x = 3 , res.y = 1; 
	f.v[1][1] = f.v[1][2] = f.v[2][2] = f.v[2][3] = 1 , f.v[3][2] = res.v[1][1] = res.v[2][1] = res.v[3][1] = 1;
	f.v[1][3] = f.v[2][1] = f.v[3][1] = f.v[3][3] = 0 ;
	f = matrix_power( f , n - 1 );
	res = f * res;
	return res.v[1][1];
}


int main()
{
	cin >> n >> m;
	cout << fib() << endl;
}

Lougu P1939 矩阵加速

矩阵快速幂的模板题，推到过程很简单

\[a[i] = 1\times a[i-1] + 0\times a[i-2]+1\times a[i-3]\\ a[i-1] = 1\times a[i-1] + 0\times a[i-2]+0\times a[i-3]\\ a[i-2] = 0\times a[i-1] + 1\times a[i-2]+0\times a[i-3]\\ \Downarrow \\ \begin{bmatrix}f[i]\\f[i-1]\\f[i-2]\end{bmatrix}=\begin{bmatrix}1&0&1\\1&0&0\\0&1&0\end{bmatrix}\times \begin{bmatrix}f[i-1]\\f[i-2]\\f[i-3]\end{bmatrix} \]

直接暴力矩阵快速幂是可以过的，但有没有优化呢？

我们考虑离线来做这道题

首先我们把所有的数据读入，然后离散化，并排序

对与$ans_i$我们可以计算$d=n_i-n_i$得到一个差值

然后只需将$ans_{i-1}$乘上状态转移矩阵$f$的$d$次方，就是$ans_i$

可以通过这种操作来减少多次重复的运算

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 105 , M = 5 , mod = 1e9 + 7;
int n , key[N] , val[N] , ans[N];

struct matrix
{
	int x , y;
	LL v[M][M];
	
	matrix() { memset( v , 0 , sizeof(v) ); }
	
	inline friend matrix operator *  (matrix a , matrix b )
	{
		register matrix cur;
		cur.x = a.x , cur.y = b.y;
		for( register int i = 1 ; i <= cur.x ; i ++ )
		{
			for( register int j = 1 ; j <= cur.y ; j ++ )
			{
				cur.v[i][j] = 0;
				for( register int k = 1 ; k <= a.y ; k ++ ) cur.v[i][j] = ( cur.v[i][j] + a.v[i][k] % mod * b.v[k][j] % mod ) % mod;
			}
		}
		return cur;
	}
} f , res;


inline LL read()
{
	register LL x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline void matrix_I( matrix &t , int k)//构造单位矩阵
{
	t.x = t.y = k;
	for( register int i = 1 ; i <= k ; i ++ ) t.v[i][i] = 1;
}

inline matrix matrix_power( matrix x , int k )//矩阵快速幂
{
	if( k == 1 ) return x;
	register matrix t; matrix_I( t , 3 );
	while( k )
	{
		if( k & 1 ) t = t * x ;
		x = x * x;
		k >>= 1;
	}
	return t;
}

inline void init()
{
	f.x = f.y = 3;
	memset( f.v , 0 , sizeof( f.v ) );
	f.v[1][1] = f.v[1][3] = f.v[2][1] = f.v[3][2] = 1 ;
}


int main()
{
	n = read();
	for( register int i = 1 ; i <= n ; i ++ ) key[i] = val[i] = read();
	sort( val + 1 , val + 1 + n ) ;
	for( register int i = 1 ; i <= n ; i ++ ) key[i] = lower_bound( val + 1 , val + 1 + n , key[i] ) - val;
	res.x = 3 , res.y = res.v[1][1] = res.v[2][1] = res.v[3][1] = 1;
	val[0] = 3;
	for( register int i = 1 ; i <= n ; i ++ )
	{
		if( val[i] <= 3 ) { ans[i] = 1 , val[i] = 3 ; continue; }
		register int d = val[i] - val[ i - 1 ];//计算差值
		if( d == 0 ) //特殊情况
		{
			ans[i] = ans[ i - 1 ] ;
			continue;
		}
		init();//初始化 矩阵f 
		f = matrix_power( f , d );
		res = f * res;
		ans[i] = res.v[1][1] % mod;
	}
	for( register int i = 1 ; i <= n ; i ++ ) printf( "%d\n" , ans[ key[i] ] );
	return 0;
}

0x35组合数学

加法原理

若完成一件事有$n$类，第$i$类有$a_i$中方法，那么完成这件事共有$a_1+a_2+\cdots+a_n$种方法

乘法原理

若完成一件事$n$个步骤，第$i$个步骤有$a_i$种方法，那么完成这件事共有$a_1\times a_2\times \cdots\times a_n$种方法

排列数

假设有这样一个问题：现在有甲乙丙丁四个小朋友，老师想从中挑出两个小朋友排成一列，有几种排法。
很容易枚举出来，有12种排法：

甲乙，甲丙，甲丁，乙甲，乙丙，乙丁，丙甲，丙乙，丙丁，丁甲，丁乙，丁丙

但问题假如变成从$66666$个小朋友中挑出$2333$个小朋友有几种排法，显然枚举是不现实的。我们需要一个通用的计算方法。

排列就是指这类问题。它的定义是：从$m$个不同的元素中取出$n$ ($0\leq n\leq m$)个元素排成一列的方法数。记作$A_{m}^{m}$。
我们可以一步一步的考虑这个问题，首先从$m$个小朋友中抽取一个放在第一个有$m$种方法。之后从剩下的$m-1$个中挑一个放在第二个即有$m-1$中方法。以此类推，根据乘法原理我们可以得到

\[A_{m}^{n} = m \times (m-1) \times (m-2) \times \cdots \times (m-n+1) \]

通过化简我们可以得到

\[A_{m}^{n} = \frac{m!}{(m-n)!} \]

PS：阶乘$n! = 1 \times 2 \times 3 \times \cdots \times n$。特别的我们规定$0! = 1$。

组合数

如果老师只是先从4个小朋友中挑出2人组成一组，不用考虑排列顺序呢么有几种呢？很显然通过枚举得知有6种

甲乙，甲丙，甲丁，乙丙，乙丁，丙丁

组合数就是指这类问题。它的定义是：从$m$个不同的元素中取出$n$ ($0\leq n\leq m$)个元素组成一组的方法数。记作$C_{m}^{m}$。注意与排列不同的是不考虑顺序。
呢么我们就要重新推到，类比刚才的结论我们得知排列只是将组合的每种结果进行了不同的排序。反而言之对于组合来说，排序是重复的。重复的情况是每个组合的排序。呢么对于每个组合重复了多少种情况呢。相当于从$n$个小朋友种抽出$n$个小朋友排一对，也就是

\[A_{n}^{n} = \frac{n!}{(n-n)!} = \frac{n!}{0!} = n!\]

\[排序是对组合的每种情况进行排序，根据乘法原理 \]

A_{m}^{n} = C_{m}^{n} \times A_{n}^{n}

\[所以我们得到 \]

C_{m}^{n} = \frac{m!}{(m-n)! \times n!}

\[ 性质： 1. $C_n^m=C_n^{n-m}$ 2. $C_n^m=C_{n-1}^{m}+C_{n-1}^{m-1}$ 3. $C_n^0+C_n^1+\cdots +C_n^n=2^N$ 4. $C_n^0+C_n^2+C_n^4+\cdots = C_n^1+C_n^3+C_n^5\cdots=2^{n-1}$ ## 组合数的计算 ### 加法递推$O(n^2)$ 利用性质2，边界条件$C_n^0=C_n^n=1$，其实就是杨辉三角 ```cpp for( register int i = 0 ; i <= n ; i ++ ) { c[i][0] = 1; for( register int j = 1 ; j <= i ; j ++) c[i][j] = c[i-1][j] + c[i-1][j-1]; } ``` ### 乘法地推$O(n)$ $C_n^m=\frac{n-m+1}{n}\times C_n^{m-1}$，边界条件$C_n^0=1$。必须先乘后除，不然可能除不开可以利用性质$1$，减少部分运算 ```cpp c[0] = 1; for( register int i = 1 ; i * 2 <= n ; i ++ ) c[i] = c[n-i] = ( n - i + 1 ) * c[ i - 1 ] / i; ``` ## 生成全排列一些题目可能会给定一串数字，要求找到其中的某一个顺序，暴力的做法就是生存这个序列的全排列，然后暴力判断这里提供一个$STL$来生成全排列`next_permutation` `next_permutation`是生成当前序列的下一个序列，直到整个序列单调递减 ```cpp int a[3]; do { for( register int i = 0 ; i < 3 ; i ++ ) cout << a[i] << ' '; cout << endl; }while( next_permutation( a , a + 3 ) ); ``` 当然`next_permutation`也可以只针对某一段生成排列，修改参数即可，同时也支持自定义排序方式，类似`sort` 注意`next_permutation`操作的序列必须是单调递增，不然只能生成当前序列的下一个序列，无法生成所有的序列 ## 枚举子集如果用一个数的二进制来表示一个集合，那么就可以用下面的方法生成当前集合的所有子集，并能做到不重不漏 ```cpp for( register int i = s ; i ; i = ( i - 1 ) & s ); ``` ## 二项式定理 \]

(a+b)^n=\sum_{k=0}C_n^kab^{k}

\[ ## [NOIP2011计算系数](<https://loj.ac/problem/2599>) 二项式定理的模板题直接计算即可 ```cpp #include <bits/stdc++.h> #define LL long long using namespace std; const int N = 1e6+5; const LL mod = 10007; LL a,b,k,n,m,result = 1,t[N]; inline LL gcd(LL a,LL b) {return !b?a:gcd(b,a%b);} inline LL ksm(LL a,LL b) { register LL ans = 1; while(b) { if(b & 1) ans = (ans * a) % mod; a = (a * a) % mod; b >>= 1; } return ans % mod; } int main() { cin >> b >> a >> k >> n >> m; result = (result * ksm(b,n)) % mod; result = (result * ksm(a,m)) % mod; n = min(n,m); for(register int i = 1,j = k - n + 1;i <= n;i ++,j ++) t[i] = j; for(register int i = 2;i <= n;i ++) { register LL x = i,y; for(register int j = 1;j <= n;j ++) { if(x > t[j]) y = gcd(x,t[j]); else y = gcd(t[j],x); if(y == 1) continue; x /= y; t[j] /= y; if(x == 1) break; } } for(register int i = 1;i <= n;i ++) result = (result * t[i]) % mod; cout << result << endl; } ``` ## Catalan数列给定$n$个$0$和$n$个$1$,他们按照某种顺序排列成长度为$2n$的序列，满足任意前缀中$0$的个数都不少于$1$的个数的序列的数量为 \]

Cat_n=\frac{1}{n+1}\times C_{2n}^{n}

\[推论： 1. $n$个左括号和$n$个右括号组成的合法序列为$Cat_n$ 2. $1,2,3,\cdots n$经过一个栈形成的合法出栈顺序为$Cat_n$ 3. $n$个节点构成不同的二叉树的数量为$Cat_n$ 4. 在平面直角 ## Lucas定理若$p$是质数，则对于任意的整数$1\le m \le n$，有： \]

C_n^m=C_{n\mod p}^{m\mod p}\times C_{n/p}^{m/p}(\mod P)

\[ ## [Loj 10228. 组合](<https://loj.ac/problem/10228>) 卢卡斯定理的模板题，组合数根据定义直接求 [Luogu P3807卢卡斯定理](<https://www.luogu.org/problem/P3807>)小细节不同 ```cpp #include <bits/stdc++.h> #define LL long long using namespace std; LL p; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline LL power( LL x , LL y ) { register LL res = 1; while( y ) { if( y & 1 ) res = ( res * x ) % p; x = ( x * x ) % p; y >>= 1; } return res; } inline LL inv ( LL x ) { return power( x , p - 2 ) % p ; } inline LL C ( LL n , LL m ) { if( m > n ) return 0; LL a = 1 , b = 1; for( register LL i = n - m + 1 ; i <= n ; i ++ ) a = a * i % p; for( register LL i = 2 ;i <= m ; i ++ ) b = b * i % p; return a * inv( b ); } inline LL lucas( LL n , LL m ) { if( !m ) return 1; return C( n % p , m % p ) * lucas( n / p , m / p ) % p; } int main() { for( register int T = read() , n , m ; T >= 1 ; T -- ) n = read() , m = read() , p = read() , printf( "%lld\n" , lucas( n , m ) ); return 0; } ``` # 0x3e补充证明 ## part 1. 已知$t = x+y,a^x\equiv1(mod\ n),a^t \equiv 1(mod \ n)$ 求证$a^y\equiv 1(mod\ n)$ 证明 \]

由已知式子得a^x=k_1 \times n+1\
设a^y=k_2\times n + p\
则a^t=ax\times a^y=k_1k_2n2+(tk_1+k_2)n+t\
又因为a^t% n=1,所以t=1\
所以a^y\equiv1(mod\ n)

\[ ## 证明素数是无数个假设数是$n$个，每个素数是$p_i$ 令$P = \Pi_{i=1}^{n} pi + 1$ 因为任何一个数都可以分解成多个质数相乘所以$P$除以任何一个质数都余$1$ 显然$P$就也是一个质数与假设矛盾，所以假设错误所以质数是无限个 **PS** $P = \Pi_{i=1}^{n} pi + 1$不是质数的通项公式举例$ n = 2 $ 则$P = 2 \times 3 + 1 = 7$ 显然第三个质数是$5$ 所以这个式子只能用于证明素数是无限个，并不是质数的通项公式目前人类还没有发现质数的通项公式，只有近似公式 ## 求斐波那契数列通项公式已知$F_{n+2} = F_{n+1} + F_n$ 其中$F_1 = F_2 = 1$ ,求$F_n$通项公式首先令首项为$1$公比为$x$的等差数列$\{ x^n \}$ 满足$F_n$的递推式代入递推式得$x^{n+2}=x^{n+1} + x^{n}$ 整理得$(x^2-x-1)x^n = 0$ 因为$x^n\neq 0 $ 所以$x^2-x-1=0$ 解得$x_1=\frac{1+\sqrt{5}}{2}$或$x_2=\frac{1-\sqrt{5}}{2}$ 所以数列${x_1^n}$和${x_2^n}$都满足$F_n$的递推公式，但${x_1^n}$和${x_2^n}$都不是斐波那契数列的通项公式构造$F_n = ax_1^n+bx_2^n$ 证明 $F_{n+2} = ax_1^{n+2} + bx_2^{n+2} =a(x_1^nx_1^2) +b(x_2^nx_2^2)$ 因为$x_1^2=x_1+1,x_2^2=x_1+1$ 所以$F_{n+2}=ax_1^n(x_1+1)+bx_2^n(x_2+1) = ax_1^{n+1}+bx_2^{n+1}+ax_1^n+bx_2^n =F_{n+1}+F_n$ 所以$F_n = ax_1^n+bx_2^n$ 已知$F_1=1,F_2=1$，代入得 $\left \{\begin{matrix} ax_1+bx_2=1 \\a^2x_1^2+b^2x_2^2=1 \end{matrix} \right .$ 解得 $a=\frac{1}{\sqrt{5}},b=-\frac{1}{\sqrt{5}}$ 所以 \]

F_n=\frac{\sqrt{5}}{5}[(\frac{1+\sqrt{5}}{2})^{n-(\frac{1-\sqrt{5}}{2})}n]

\[ # 0x41 并查集 ## 定义在计算机科学中，并查集是一种树型的数据结构，用于处理一些不交集的合并及查询问题。有一个联合-查找算法定义了两个用于此数据结构的操作： - $Find$：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。 - $Union$：将两个子集合并成同一个集合。由于支持这两种操作，一个不相交集也常被称为联合-查找数据结构或合并-查找集合。其他的重要方法，$MakeSet$，用于创建单元素集合。有了这些方法，许多经典的划分问题可以被解决。为了更加精确的定义这些方法，需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素，称为代表，以表示整个集合。接着，$Find(x)$ 返回 $x$ 所属集合的代表，而 $Union $使用两个集合的代表作为参数。 ## 路径压缩与按秩合并这是两个并查集常用的优化当我们在寻找祖先时，一旦元素多且来，并查集就会退化成单次$O(n)$的算法，为了解决这一问题我们可以在寻找祖先的过程中直接将子节点连在祖先上，这样可以大大降低复杂度，均摊复杂度是$O(log(n))$的按秩合并也是常见的优化方法，“秩”的定义很广泛，举个例子，在不路径压缩的情况下，常见的情况是把子树的深度定义为秩无论如何定义通常情况是把“秩”储存在根节点，合并的过程中把秩小的根节点插到根大的根节点上，这样可以减少操作的次数特别的，如果把秩定义为集合的大小，那么采用了按秩合并的并查集又称“启发式并查集” 按秩合并的均摊复杂度是$O(log(n))$的，如果同时采用按秩合并和路径压缩均摊复杂度是$O(\alpha(n) )$,$\alpha(n)$是反阿克曼函数 \]

\forall n \le 2^{10{19729}},\alpha(n)\le 5

\[可以视为均摊复杂度为$O(1)$ 不过通常情况下我们仅采用路径压缩即可 ```cpp int father[N]; int getfather( int x )//查询 { if( father[x] == x ) return x; return father[x] = getfather( father[x] ); } inline void union( int x , int y )//合并 { register int fx = getfather( x ) , fy = getfather( y ); father[ fx ] = fy; return ; } inline bool same( int x , int y ) { return getfather( x ) == getfather( y ) ;} //判读是否在同一结合 //把深度当作秩的按秩合并 memset( rank , 0 , sizeof( rank ) ); inline void rank_union( int x , int y ) { fx = getfather( x ) , fy = getfather( y ); if( rank[ fx ] < rank[ fy ] ) ) father[ fx ] = fy; else { father[ fy ] = fx; if( rank[ fx ] == rank[ fy ] ) rank[ fx ] ++; } return ; } ``` ## [NOI2015 程序自动分析](<https://www.luogu.org/problem/P1955>) 虽然是$noi$的题但总体还是很简单的，本质就是维护一个并查集根据操纵把相同的全部合并，在把逐一判断不相同的为什么不能反过来做呢？举个例子$a\ne b,b\ne c$能否推出$a\ne c$呢？显然不能为什么？因为不等关系没有传递性那为什么相同可以呢？因为相同是有传递性的所以从本题也可知并查集维护的一定要具有传递性那么剩下的就数据比较大，但$n\le 1e6$所以离散化即可 ```cpp #include <bits/stdc++.h> #define PII pair< int , int > #define S second #define F first using namespace std; const int N = 1e6+5; int n , cur[ N * 2 ] , fa[ N * 2 ] , ta , tb , cnt; PII a[N] , b[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline int getfa( int x ) { if( x == fa[x] ) return x; return fa[x] = getfa( fa[x] ); } inline void work() { cnt = ta = tb = 0; n = read(); for( register int i = 1 , u , v , w ; i <= n ; i ++ ) { u = read() , v = read() , w = read(); cur[ ++ cnt ] = u , cur[ ++ cnt ] = v; if( w ) a[ ++ ta ] = { u , v }; else b[ ++ tb ] = { u , v }; } sort( cur + 1 , cur + 1 + cnt ); cnt = unique( cur + 1 , cur + 1 + cnt ) - cur - 1; for( register int i = 1 ; i <= cnt ; i ++ ) fa[i] = i; register int fx , fy; for( register int i = 1 ; i <= ta ; i ++ ) { a[ i ].F = lower_bound( cur + 1 , cur + 1 + cnt , a[i].F ) - cur; a[ i ].S = lower_bound( cur + 1 , cur + 1 + cnt , a[i].S ) - cur; fx = getfa( a[i].F ) , fy = getfa( a[i].S ); fa[ fx ] = fy; } for( register int i = 1 ; i <= tb ; i ++ ) { b[ i ].F = lower_bound( cur + 1 , cur + 1 + cnt , b[i].F ) - cur; b[ i ].S = lower_bound( cur + 1 , cur + 1 + cnt , b[i].S ) - cur; fx = getfa( b[i].F ) , fy = getfa( b[i].S ); if( fx != fy ) continue; puts("NO"); return ; } puts("YES"); return ; } int main() { for( register int T = read() ; T ; T -- ) work(); return 0; } ``` ## 带权并查集我们在维护并查集实际的过程中额外的在维护一个$dis$代表从当前的点到根节点的距离。由于路径压缩导致每次访问后都会将所以的点指向根节点。所以我们要在每次维护的过程中更新$dis$数组，此时需要我们在维护一个$size$数组，代表在每个根节点的子树的大小，怎样我们合并的过程中就可以把根节点$x$插到根节点$y$的后面，并且让$dis[x]+=size[y]$。这样我们就可以在压缩路径的过程中，不断的更新每个节点到根节点的距离注意这里的情况说的是，每个树都是一条链，且每次都是将一条链接在另一条链的后面那么如果是将任意一颗子树插到另一颗子树的任意一个节点怎么办办呢？并且我还要压缩路径，其实是可以的我们并且只用两个数组$father$和$dis$就可以实现 ```cpp int father[N] , dis[N] inline int getfather( int x ) { if( father[x] == x ) return x; register int root =getfather( father[x] ); dis[x] = dis[ father[x] ] + 1; return father[x] = root; } inline void merge( int x , int y )//把根节点x 插到结点y 上 { register int fx = getfather( x ) , fy = getfather( y ); fa[x] = fy; dis[fx] += dis[y] + 1 ; return ; } inline void init()//初始化 { for( register int i = 1 ; i <= n ; i++ ) father[i] = i; } ``` 注意这里的$x$必须是根节点假设我们要把$x$插到$y$上，我们直接用$dis[y]+1$来更新$dis[x]$，对于$x$的子节点我们可以在递归的时候修改注意，如果需要使用$dis[x]$在用之前必须要先调用一次$getfather(x)$，来更新一下$dis[x]$和$fahter[x]$ 所以时间复杂度可能会略高，但没有具体证明，因为这个算法是一天中午我自己琢磨出来的，且没有在网上找严格的证明 ## [ NOI2002 银河英雄传说](<https://www.luogu.org/problem/P1196>) 这就是到带权并查集的模板，所以在没有在上面放代码可以直接琢磨下这个代码 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 30005; int fa[N] , dis[N] ,size[N] , n ; char opt; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline int getfa( int x ) { if( fa[x] == x ) return x; register int root = getfa( fa[x] ); dis[ x ] += dis[ fa[x] ]; return fa[x] = root; } inline void merge( int x , int y ) { x = getfa( x ) , y = getfa( y ); fa[ x ] = y, dis[ x ] += size[ y ] , size[y] += size[x] , size[ x ] = 0; return ; } inline int query( int x , int y ) { register int fx = getfa( x ) , fy = getfa( y ); if( fx != fy ) return - 1; return abs( dis[x] - dis[y] ) - 1; } int main() { n = read(); for( register int i = 1 ; i < N ; i ++ ) fa[i] = i , size[i] = 1 ; for( register int u , v ; n ; n -- ) { do{ opt = getchar() ; }while( opt != 'C' && opt != 'M' ); u = read() , v = read() ; if(opt == 'M') merge( u , v ); else printf( "%d\n" , query( u , v ) ); } return 0; } ``` ## 扩展域并查集扩展域并查集就是将并查集的区域大小扩展成整数倍，用多个区域来同时维护多个传递关系 ## [AcWing 239. 奇偶游戏](<https://www.acwing.com/problem/content/241/>) 这是一道经典的扩展域并查集首先我们用一个$sum[x]$数组，代表从$1$到$x$的$1$的个数如果当前询问的答案是$even$也就是偶数，那么$sum[l-1]$与$sum[r]$的寄偶性应该相同如果当前询问的答案是$odd$也就是寄数，那么$sum[l-1]$与$sum[r]$的寄偶性应该不相同所以我们可以建一个大小为$2n$的并查集，其中$1\cdots n$表示偶数的关系、$n+1\cdots 2n$表示奇数为了表示方便我们定义两个变量$x\_even=x,x\_odd=x+n$ 如果奇数的话我们就把$x\_even$和$y\_odd$合并，$x\_odd$和$y\_even$合并如果偶数的话我们就把$x\_odd$和$y\_odd$合并，$x\_even$和$y\_even$合并另外在每次合并前都要判断一下时候正确 ```cpp #include <bits/stdc++.h> #define PII pair< int , int > #define PIIB pair < PII , bool > #define F first #define S second #define hash( x ) ( lower_bound( a + 1 , a + 1 + n , x ) - a ) using namespace std; const int N = 10010; int a[ N << 1 ] , n , m , fa[ N << 2 ]; PIIB opt[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline int getfa( int x ) { if( fa[x] == x ) return x; return fa[x] = getfa( fa[x] ); } int main() { n = read() , m = read() , n = 0; register string str; for( register int i = 1 ; i <= m ; i ++ ) { opt[i].F.F = read() , opt[i].F.S = read(); a[ ++ n ] = opt[i].F.F - 1 , a[ ++ n ] = opt[i].F.S; cin >> str; if( str == "even" ) opt[i].S = 1; else opt[i].S = 0; } //离散化 sort( a + 1 , a + 1 + n ); n = unique( a + 1 , a + 1 + n ) - a - 1 ; for( register int i = 1 ; i <= m ; i ++ ) opt[i].F.F = hash( opt[i].F.F - 1 ) , opt[i].F.S = hash( opt[i].F.S ); for( register int i = 1 ; i <= 2 * n ; i ++ ) fa[i] = i; for( register int i = 1 , x_even , x_odd , y_even , y_odd ; i <= m ; i ++ ) { x_even = getfa( opt[i].F.F + n ) , x_odd = getfa( opt[i].F.F ) , y_even = getfa( opt[i].F.S + n ) , y_odd = getfa( opt[i].F.S ); if( opt[i].S ) // 不同 { if( x_odd == y_even ) printf( "%d\n" , i - 1) , exit(0); fa[ x_even ] = y_even , fa[ x_odd ] = y_odd; } else// 相同 { if( x_even == y_even ) printf( "%d\n" , i - 1 ) , exit(0); fa[ x_even ] = y_odd , fa[ x_odd ] = y_even; } } printf( "%d\n" , m ); return 0; } ``` ## [NOI2001 食物链](<https://www.luogu.org/problem/P2024>) 经典的扩展域并查集，我们可以开三个域，同类，食物，天敌，来维护这样一个集合同样为了方便表示，分别用$x_a,x_b,x_c$表示$x$的同类，$x$的食物，$x$的天敌如果$x$和$y$是同类，就把$x_a$和$y_a$合并、$x_b$和$y_b$合并、$x_c$和$y_c$合并如果$x$吃$y$，就把$x_a$和$y_c$合并、$x_b$和$y_a$合并、$x_c$和$y_b$合并所以针对每次操作前想判断是否出现冲突，在进行合并即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 5e4 + 5; int n , m , cnt , fa[ N * 3 ]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 1 ) + ( x << 3 ) + ch - '0'; ch = getchar(); } return x; } inline int getfa( int x ) { if( fa[x] == x ) return x; return fa[x] = getfa( fa[x] ); } int main() { n = read() , m = read(); for( register int i = 1 ; i <= n * 3 ; i ++ ) fa[i] = i; for( register int opt , x , y , x_a , x_b , x_c , y_a , y_b , y_c ; m >= 1 ; m -- ) { opt = read() , x = read() , y = read(); x_a = getfa( x ) , x_b = getfa( x + n ) , x_c = getfa( x + 2 * n ) , y_a = getfa( y ) , y_b = getfa( y + n ) , y_c = getfa( y + 2 * n ); // x_a x的同类 x_b x的食物 x_c x的天敌 if( x > n || y > n || ( opt == 2 && x == y ) ) { cnt ++ ; continue; } if( opt == 1 ) { if( x_b == y_a || x_c == y_a ) { cnt ++ ; continue ; } fa[ x_a ] = y_a , fa[ x_b ] = y_b , fa[ x_c ] = y_c; } else { if( x_a == y_a || x_c == y_a ) { cnt ++ ; continue ; } fa[ x_a ] = y_c , fa[ x_b ] = y_a , fa[ x_c ] = y_b; } } cout << cnt << endl; return 0; } ``` ## [NOIP2017 奶酪](<https://www.luogu.org/problem/P3958>) 这道题是$NOIP2017$来的一道题，这道题也是我第一次参加联赛遇到题，考场上我并没有看出这是道并查集这道题其实很暴力因为$n$的范围比较小，我么可以直接$O(N^2)$暴力枚举，然后用并查集判断即可，在随后枚举与上下底面相交或相切的圆判断是否在一个集合里即可 ```cpp #include <bits/stdc++.h> #define LL long long #define PII pair< LL , LL > #define PIII pair < PII , LL > #define F first #define S second #define pb( x ) push_back( x ) #define square( x ) ( x * x ) using namespace std; const int N = 1005; LL n , h , r , fa[N] ; vector < LL > Floor , Roof; vector < PIII > node; inline LL read() { register LL x = 0 , f = 1; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f; } inline LL getfa( LL x ) { if( x == fa[x] ) return x; return fa[x] = getfa( fa[x] ); } inline void merge( LL x , LL y ) { x = getfa( x ) , y = getfa( y ); fa[x] = y; return ; } inline bool pending( LL x , LL y ) { return ( square( ( node[x].F.F - node[y].F.F ) ) + square( ( node[x].F.S - node[y].F.S ) ) + square( ( node[x].S - node[y].S ) ) ) <= r * r * 4 ; } inline void work() { n = read() , h = read() , r = read() , node.clear() , Floor.clear() , Roof.clear(); for( register int i = 0 , x , y , z ; i < n ; i ++ ) { fa[i] = i , x = read() , y = read() , z = read(); node.push_back( { { x , y } , z } ); if( z - r <= 0 ) Floor.push_back( i ); if( z + r >= h ) Roof.push_back( i ); } for( register int i = 0 ; i < n ; i ++ ) { for( register int j = i + 1 ; j < n ; j ++ ) { if( pending( i , j ) ) merge( i , j ); } } for( auto i : Floor ) { for( auto j : Roof ) { if( getfa( i ) != getfa( j ) ) continue; puts("Yes"); return ; } } puts("No"); return ; } int main() { for( register int T = read() ; T >= 1 ; T -- ) work(); return 0; } ``` # 0x42 树状数组树状数组这里就不讲原理了，给张图自己理解即可 ![](https://cdn.luogu.com.cn/upload/image_hosting/cgi4zipq.png) 注意树状数组维护的数组下标必须是$1\cdots n$，如果有$0$就会死循环 ## [Loj 130. 树状数组 1 ：单点修改，区间查询](<https://loj.ac/problem/130>) 模板题直接看代码即可 ```cpp #include <bits/stdc++.h> #define lowbit( x ) ( x & -x ) #define LL long long using namespace std; const int N = 1e6 + 5; LL n , m , bit[N]; inline LL read() { register LL x = 0 , f = 1 ; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f ; } inline void add( LL x , LL w ) { for( register int i = x ; i <= n ; i += lowbit( i ) ) bit[i] += w; } inline LL find( LL x ) { register LL sum = 0; for( register int i = x ; i >= 1 ; i -= lowbit( i ) ) sum += bit[i]; return sum; } int main() { n = read() , m = read(); for( register int i = 1 , x ; i <= n ; i ++ ) x = read() , add( i , x ); for( register int i = 1 , opt , x , y ; i <= m ; i ++ ) { opt = read() , x = read() , y = read(); if( opt == 1 ) add( x , y ); else printf( "%lld\n" , find( y ) - find( x - 1 ) ); } return 0; } ``` ## [Loj 10116. 清点人数](<https://loj.ac/problem/10116>) 模板题，没啥好解释的，之前看模板就能写出来 ## [Loj 131. 树状数组 2 ：区间修改，单点查询](<https://loj.ac/problem/131>) 区间修改也是树状数组的经典操作，简单来说就是维护一个差分序列 ```cpp #include <bits/stdc++.h> #define LL long long #define lowbit( x ) ( x & - x ) using namespace std; const int N = 1e6 + 1000; LL n , m , bit[N]; inline LL read() { register LL x = 0 , f = 1; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f; } inline LL add( LL x , LL w ) { for( register int i = x ; i <= n ; i += lowbit( i ) ) bit[i] += w ; } inline LL find( LL x ) { register LL sum = 0; for( register int i = x ; i >= 1 ; i -= lowbit( i ) ) sum += bit[i]; return sum; } int main() { n = read() , m = read(); for( register LL i = 1 , last = 0 , x ; i <= n ; i ++ ) x =read() ,add( i , x - last ) , last = x ; for( register LL i = 1 , opt , l , r , w ; i <= m ; i ++ ) { opt = read(); if( opt == 1 ) { l = read() , r = read() , w = read(); add( l , w ) , add( r + 1 , -w ); } else printf("%lld\n" , find( read() ) ); } return 0; } ``` ## [Loj 10117.简单题](<https://loj.ac/problem/10117>) 还是到模板题，直接套板子吧 ## [Loj 132. 树状数组 3 ：区间修改，区间查询](<https://loj.ac/problem/132>) 联系上一道题，我们假设原数组是$a[i]$维护一个差分数组$d[i]$自然可以得到 \]

\sum_{i=1}^{{n}a[i]=\sum_{i=1}}\sum_{j=1}^{i}d[i]

\[然后我们发现$d[1]$用了$p$次，$d[2]$用了$p-1$次，$d[i]$用了$p-i+1$次，所以可以得到 \]

\sum_{i=1}^{{n}\sum_{j=1}}d[i]=\sum_{i=1}^{{n}d[i]\times(n-i+1)=(n+1)\times\sum_{i=1}}d[i]\times\sum_{i=1}^{n}(d[i]\times i)

\[所以我们可以同时维护两个数组$sum1[i]=\sum d[i],sum2[i]=\sum (d[i]\times i)$ 查询查询位置$p$，$(p+1)$乘以$sum1$种$p$的前缀减去$sum2$中$p$的前缀查询$[l,r]$的区间和，$r$的前缀减$l-1$的前缀修改对于$sum1$中的修改类似与上一个问题的修改对于$sum2$中的修改，给$sum2[l]+=l\times x , sum2[r+1]-=(r+1)\times x$ ```cpp #include <bits/stdc++.h> #define LL long long #define lowbit( x ) ( x & - x ) using namespace std; const int N = 1e6 +5; int n , m ; LL sum1[N] , sum2[N]; inline int read() { register int x = 0 , f = 1; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f; } inline void add( int x , LL w ) { for( register int i = x ; i <= n ; i += lowbit( i ) ) sum1[i] += w , sum2[i] += w * x; } inline LL find( int x ) { register LL s = 0 , t = 0 ; for( register int i = x ; i >= 1 ; i -= lowbit( i ) ) s += sum1[i] , t += sum2[i]; return ( x + 1 ) * s - t; } int main() { n = read() , m = read(); for( register int i = 1 , x , last = 0 ; i <= n ; i ++ ) x = read() , add( i , x - last ) , last = x ; for( register int i = 1 , opt , l , r , w ; i <= m ; i ++ ) { opt = read(); if( opt == 1 ) l = read() , r = read() , w = read() , add( l , w ) , add( r + 1 , - w ); else l = read() , r = read() , printf( "%lld\n" , find( r ) - find( l - 1 ) ); } return 0; } ``` ## [Loj 10114.数星星 Stars](<https://loj.ac/problem/10114>) 根据树状数组的性质我们可以快速的求出前$k$个数的和，加上坐标是递增给的，我们可以在每次插入前统计在当前星星之前有多少个星星即可，显然纵坐标是没有用的注意坐标是从$(0,0)$开始的，但树状数组的下标是从$1$开始所以给坐标整体加$1$即可p ```cpp #include <bits/stdc++.h> #define lowbit( x ) ( x & - x ) using namespace std; const int N = 15e3 + 5 , M = 32010; int n , bit[M] , level[N]; inline int read() { register int x = 0 , f = 1 ; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f ; } inline void add( int x , int w ) { for( register int i = x ; i <= 32001 ; bit[i] += w , i += lowbit( i ) ); } inline int find( int x ) { register int sum = 0; for( register int i = x ; i >= 1 ; i -= lowbit( i ) ) sum += bit[i]; return sum; } int main() { n = read(); for( register int i = 1 , x ; i <= n ; x = read() + 1 , read() , level[ find(x) ] ++ , add( x , 1 ) , i ++ ); for( register int i = 0 ; i < n ; printf( "%d\n" , level[i] ) , i ++ ); return 0; } ``` ## [Loj 10115.校门外的树](<https://loj.ac/problem/10115>) 我们把每次种树抽象成一个线段，同时开两个树状数组分别维护每条线段的两个端点插入时在$l$处增加一个左端点，$r$处增加一个右端点查询时查询$1\cdots r $的右端点个数，$1\cdots l$的左端点个数，做差就是$l\cdots r$中线段的个数 ```cpp #include <bits/stdc++.h> #define lowbit( x ) ( x & - x ) using namespace std; const int N = 5e4 + 5; int n , m , bit[2][N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while ( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int w , int k ) { for( register int i = x ; i <= n ; i += lowbit( i ) ) bit[k][i] += w ; } inline int find( int x , int k ) { register int res = 0 ; for( register int i = x ; i >= 1 ; i -= lowbit( i ) ) res += bit[k][i]; return res; } int main() { n = read() , m = read(); for( register int i = 1 , op , l , r ; i <= m ; i ++ ) { op = read() , l = read() , r = read(); if( op == 1 ) add( l , 1 , 0 ) , add( r , 1 , 1 ); else printf( "%d\n" , find( r , 0 ) - find( l - 1 , 1 ) ); } return 0; } ``` ## [Luogu P1908 逆序对](<https://www.luogu.org/problem/P1908>) 逆序对是树状数组的经典操作，其实相当于用树状数组维护了一个桶 ```cpp #include <bits/stdc++.h> #define lowbit( x ) ( x & - x ) #define LL long long using namespace std; const int N = 5e5 + 5 ; int n , m , a[N] , b[N] , bit[N]; LL cnt ; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int w ) { for( register int i = x ; i <= n ; bit[i] += w , i += lowbit( i ) ); } inline LL find( int x ) { register LL sum = 0; for( register int i = x ; i >= 1 ; sum += bit[i] , i -= lowbit( i ) ); return sum; } int main() { n = read(); for( register int i = 1 ; i <= n ; i ++ ) a[i] = b[i] = read(); sort( b + 1 , b + 1 + n ); m = unique( b + 1 , b + 1 + n ) - b - 1; for( register int i = 1 ; i <= n ; i ++ ) a[i] = lower_bound( b + 1 , b + 1 + m , a[i] ) - b; for( register int i = n ; i >= 1 ; i -- ) { add( a[i] , 1 ); cnt += find( a[i] - 1 ); } cout << cnt << endl; return 0; } ``` ## [Loj 3195. 「eJOI2019」异或橙子](<https://loj.ac/problem/3195>) 首先先来两个引理 \]

a \oplus a = 0\0\oplus a = a

\[知道这个引理后，我们就可以看下样例 \]

a_2 \oplus a_3 \oplus a_4 \oplus (a_2 \oplus a_3) \oplus (a_3 \oplus a_4) \oplus (a_2 \oplus a_3 \oplus a_4)=a_2 \oplus a_2 \oplus a_2 \oplus a_3 \oplus a_3 \oplus a_3\oplus a_3 \oplus a_4 \oplus a_4 \oplus a_4\=a_2\oplus0 \oplus a_4= 2

\[也就是说我们可以根据异或的一些性质，来优化一下如果$a$的个数是奇数个其贡献就是$a$，如果$a$的个数是偶数个其贡献就是$0$ 手推几个数据就能发现如果$l,r$奇偶性不同所有的数都是偶数个，结果自然是$0$ 如果$l,r$奇偶性相同，那么只有和$l,r$奇偶性的位置上的数才会有贡献我们可以开两个树状数组来维护下，一个维护奇数位上的异或前缀和，另一个维护偶数位上的异或前缀和对于操作1，注意不是把第$i$位异或$j$是把$i$为修改为$j$，根据异或和的性质我们要先异或$a[i]$在异或$j$，所以可以异或$a[i]\oplus j $ 对于操作2首先特判奇偶性不同的,对于奇偶性相同的，我们在对应的树状数组里求出$r,l-1$的异或前缀和，在异或一下即可 ```cpp #include <bits/stdc++.h> #define lowbit( x ) ( x & - x ) using namespace std; const int N = 2e5 + 10; int n , m , bit[2][N] , a[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int val , int pos , int k ) { for( register int i = pos ; i <= n ; bit[k][i] ^= val , i += lowbit( i ) ); } inline int find( int pos , int k ) { register int res = 0; for( register int i = pos ; i >= 1 ; res ^= bit[k][i] , i -= lowbit( i ) ); return res; } int main() { n = read() , m = read(); for( register int i = 1 ; i <= n ; a[i] = read() , add( a[i] , i , i & 1 ) , i ++ ); for( register int i = 1 , op , l , r ; i <= m ; i ++ ) { op = read() , l = read() , r = read(); if( op == 1 ) add( a[l] ^ r , l , l & 1 ) , a[l] = r ; else printf( "%d\n" , ( ( l + r ) & 1 ) ? 0 : ( find( r , r & 1 ) ^ find( l - 1 , r & 1 ) ) ); } return 0; } ``` ## [Luogu P1168 中位数](<https://www.luogu.org/problem/P1168>) 考虑如何用树状数组做我们可以依次插入每个数比如我们要插入$x$，就个$x$个这个位置加$1$，然后$find(x)$求前缀和，就知道小于等于$x$的数有多少个然后$A_i$的范围很大，$n$的范围比较小，且我们不需要知道每个数的具体大小，只需知道相对大小即可，自然选择离散化然后就是求第$k$个数有多大，如过二分的话是$O(log^2(n))$的，比较慢根据树状数组的特性，考虑倍增，具体过程相当把`lowbit`的过程倒过来，具体可以看代码理解 ```cpp #include <bits/stdc++.h> #define lowbit( x ) ( x & -x ) using namespace std; const int N = 1e5 + 5; int n , m , a[N] , b[N] , bit[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 1 ) + ( x << 3 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int p ) { for( register int i = x ; i <= m ; i += lowbit( i ) ) bit[i] += p; } inline int find( int k ) { register int ans = 0, cnt = 0;// ans 是答案， cnt 是小于等于 ans 的数有多少个 for( register int i = 20 ; i >= 0 ; i -- ) { ans += ( 1 << i ); if( ans > m || cnt + bit[ ans ] >= k ) ans -= ( 1 << i ); else cnt += bit[ ans ]; } return ans + 1; } int main() { m = n = read(); for( register int i = 1 ; i <= n ; i ++ ) a[i] = b[i] = read(); sort( a + 1 , a + 1 + n ); m = unique( a + 1 , a + 1 + m) - a - 1;//去重 for( register int i = 1 ; i <= n ; i ++ ) b[i] = lower_bound( a + 1 , a + 1 + m , b[i] ) - a; //离散化 for( register int i = 1 ; i <= n ; i ++ ) { add( b[i] , 1 ); if( i & 1 ) printf( "%d\n" , a[find( ( i + 1 ) >> 1 )] ); } return 0; } ``` # 0x43 线段树 >线段树（英语：$Segment\ tree$)是一种二叉树形数据结构，$1977$年由$Jon Louis Bentley$发明，用以存储区间或线段，并且允许快速查询结构内包含某一点的所有区间。 > >一个包含 ${\displaystyle n}$个区间的线段树，空间复杂度为 ${\displaystyle O(n)}$，查询的时间复杂度则为 ${\displaystyle O(\log n+k)} $，其中 ${\displaystyle k}$是匹配条件的区间数量。 > >此数据结构亦可推广到高维度 ## 建树 ## ```cpp struct Node { int l , r , value , tag; Node * left , * right; // 左右子树 Node (int s , int t , int v , Node * a , Node * b) { l = s; r = t; value = v; tag = 0; left = a; right = b; } } * root; //根节点 Node * build(int l,int r) { if(l == r) return new Node( l , r , a[l] , 0 , 0 );//叶子节点 register int mid = ( l + r ) >> 1; Node * left = build( l , mid), * right = build( mid+1 , r ); // 递归构建左右子树 return new Node( l , r , left -> value + right -> value , left , right); // 建立当前节点 } ``` ## 单点修改，区间查询 ## ```cpp int find( int l , int r , Node * cur) { if(l == cur -> l && r == cur -> r) return cur -> value; // 完全包含 int mid = ( cur -> l + cur -> r ) >> 1; if( l > mid ) return find( l , r, cur -> right); // 全部在右子树 if(mid >= r) return find( l , r , cur -> left); // 全部在左子树 return find( l , mid , cur -> left) + find( mid + 1 , r , cur -> right ); // 区间跨越mid } void modify( int x , int v , Node * cur) { if(cur -> l == cur -> r ) cur -> value += v; // 叶子节点 else { int mid = (cur -> l + cur -> r ) >> 1; modify(x , v , x > mid ? cur -> right : cur -> left); cur -> value = cur -> left -> value + cur -> right -> value; } } ``` ## 区间修改，单点查询 ## 单点修改只要将$l == r$即可，所以不多做介绍 ## 区间修改，区间查询 ## 区间快速修改有两种方法 - 延迟标记 - 标记永久化（不会）考虑在每个节点维护一个标记tag，并执行以下操作 1. 如果在修改过程中当前节点被完全包含在修改区间内，给区间打上修改标记，并立刻回溯 2. 当要查询或修改当前节点的子树时，将标记下放的到子树 ```cpp inline void mark(int v,Node * cur) { cur -> tag += v; cur -> value += (cur -> r - cur -> l + 1) * v; return ; } inline void pushdown( Node * cur) { if(cur -> tag == 0) return ; if(cur -> left) { mark(cur -> tag,cur -> left); mark(cur -> tag,cur -> right); } else cur -> value += cur -> tag; cur -> tag = 0; return ; } inline int query( int l , int r , Node * cur) { if(l <= cur -> l && cur -> r <= r ) return cur -> value; register int mid = (cur -> l + cur -> r) >> 1 , res = 0; pushdown( cur ); if( l <= mid ) res += query( l , r , cur -> left ); if( mid + 1 <= r) res += query( l , r , cur -> right); return res; } void extent_modify( int l , int r , int v , Node * cur) // [l,r] + v { if(cur -> l > r || cur -> r < l) return ; if(l <= cur -> l && cur -> r <= r) { mark(v,cur); return ; } pushdown( cur ); register int mid = (cur -> l + cur -> r) >> 1; if(l <= mid) extent_modify( l , r , v , cur -> left); if(mid + 1 <= r) extent_modify( l , r , v , cur -> right); cur -> value = cur -> left -> value + cur -> right -> value; return ; } ``` ## [Luogu SP1716 GSS3 - Can you answer these queries III](<https://www.luogu.org/problem/SP1716>) 与基础的线段树操作很像，我们额外的维护三个值$dat,ldat,rdat$分别代表整个区间的最大子段和、当前区间从做左端点开始的最大子段和，从右端点开始的最大子段和考虑如何更新当前结点 ```cpp inline void update( Node * cur ) { cur -> sum = cur -> left -> sum + cur -> right -> sum; //更新sum cur -> ldat = max( cur -> left -> ldat , cur -> left -> sum + cur -> right -> ldat ); //从左起的最大子段可能是左区间的最大子段或左区间的和加右区间的最大子段 cur -> rdat = max( cur -> right -> rdat , cur -> right -> sum + cur -> left -> rdat ); //类似上面 cur -> dat = max( max( cur -> left -> dat , cur -> right -> dat ) , max( max( cur -> ldat , cur -> rdat ) , cur -> left -> rdat + cur -> right -> ldat ) ) ; //当前区间的的最大子段和要么是左右区间的的最大子段和，要么是中间的最大子段和，要么是左右端点开始的最大子段和 } ``` 也就是说线段是不止能维护区间和，实际上只要是满足结合律的都可以用线段树来维护，区间和，区间最值，区间异或和等 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 500005 , INF = 0x7f7f7f7f; int n , a[N] ; struct Node { int l , r , sum , dat , ldat , rdat ; Node * right , * left; Node( int a , int b , int c , int d , int e , int f , Node * g , Node * h ) { l = a , r = b , sum = c , dat = d , ldat = e , rdat = r , left = g , right = h ; } } * root ; inline int read() { register int x = 0 , f = 1 ; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = - 1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f; } inline void update( Node * cur ) { cur -> sum = cur -> left -> sum + cur -> right -> sum; cur -> ldat = max( cur -> left -> ldat , cur -> left -> sum + cur -> right -> ldat ); cur -> rdat = max( cur -> right -> rdat , cur -> right -> sum + cur -> left -> rdat ); cur -> dat = max( max( cur -> left -> dat , cur -> right -> dat ) , max( max( cur -> ldat , cur -> rdat ) , cur -> left -> rdat + cur -> right -> ldat ) ) ; } inline Node * build( int l , int r ) { Node * cur = new Node( l , r , 0 , 0 , 0 , 0 , NULL , NULL ); if( l == r ) { cur -> ldat = cur -> rdat = cur -> sum = cur -> dat = a[l]; return cur ; } register int mid = ( l + r ) >> 1; cur -> left = build( l , mid ); cur -> right = build( mid + 1 , r); update( cur ); return cur; } inline Node * query( int l , int r , Node * cur ) { if( l <= cur -> l && cur -> r <= r ) return cur; register int mid = ( cur-> l + cur -> r ) >> 1; if( r <= mid ) return query( l , r , cur -> left ); if( l > mid ) return query( l , r , cur -> right ); Node *res = new Node( l , r , 0 , 0 , 0 , 0 , 0 , 0 ); Node * L = query( l , r , cur -> left ) , * R = query( l , r , cur -> right ); res -> sum = L -> sum + R -> sum; res -> ldat = max( L -> ldat , L -> sum + R -> ldat ); res -> rdat = max( R-> rdat , R -> sum + L -> rdat ); res -> dat = max( max( L -> dat , R -> dat ) , max( max( res -> ldat , res -> rdat ) , L -> rdat + R -> ldat ) ); return res; } inline void change( int x , int w , Node * cur ) { if( cur -> r == x && x == cur -> l ) { cur -> sum = cur -> dat = cur ->ldat = cur -> rdat = w; return ; } register int mid = ( cur -> r + cur -> l ) >> 1; if( x <= mid ) change( x , w , cur -> left ); if( x > mid ) change( x , w , cur -> right ); update( cur ); return ; } int main() { n = read() ; for( register int i = 1 ; i <= n ; i ++ ) a[i] = read(); root = build( 1 , n ); for( register int m = read() , op , x , y ; m >= 1 ; m -- ) { op = read() , x = read() , y = read(); if( op ) printf( "%d\n" , query( x , y , root ) -> dat ); else change( x , y ,root ); } return 0; } ``` ## [Luogu P4939 Agent2](<https://www.luogu.org/problem/P4939>) 这道题用了树状数组的常用操作，说白了就是区间修改，单点查询这道题需要实现的的功能线段树也可以，但是用过代码对比和实际测试，线段树过不了，并且代码很长所以通过这道题可以得知，如果可以用树状数组的话就不要用线段树树状数组 ```cpp #include <bits/stdc++.h> #define lowbit( x ) ( x & -x ) using namespace std; const int N = 1e7 + 5; int n , m , l , r , op , bit[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int v ) { for( register int i = x ; i <= n ; i += lowbit(i) ) bit[i] += v; return ; } inline int find( int x ) { register int sum = 0; for( register int i = x ; i ; i -= lowbit(i) ) sum += bit[i]; return sum; } int main() { n = read() , m = read(); for( register int i = 1 ; i <= m ; i ++ ) { op = read(); if( op ) printf( "%d\n" , find( read() ) ); else add( read() , 1 ) , add( read() + 1 , -1 ); } return 0; } ``` 线段树 ```cpp #include <bits/stdc++.h> using namespace std; int n , m ; struct Node { int l , r , value , tag; Node * left , * right; Node( int s , int t , int w , Node * a , Node * b ) { l = s , r = t , value = w , tag = 0; left = a , right = b; } } *root; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline Node * build( int l , int r ) { if( l == r ) return new Node( l , r , 0 , 0 , 0 ); register int mid = ( l + r ) >> 1; Node * left = build( l , mid ) , * right = build( mid + 1 , r ); return new Node( l , r , 0 , left , right ); } inline void mark( int w , Node * cur ) { cur -> tag += w , cur -> value += ( cur -> r - cur -> l + 1 ) * w; } inline void pushdown( Node * cur ) { if( cur -> tag == 0 ) return ; if( cur -> left ) mark( cur -> tag , cur -> left ) , mark( cur -> tag , cur -> right ); else cur -> value += cur -> tag; cur -> tag = 0; return ; } inline int query( int l , int r , Node * cur ) { if( l <= cur -> l && cur -> r <= r ) return cur -> value; register int mid = ( cur -> l + cur -> r ) >> 1 , res = 0; pushdown( cur ); if( l <= mid ) res += query( l , r , cur -> left ); if( mid + 1 <= r ) res += query( l , r , cur -> right ); return res; } inline void modify( int l , int r , int w , Node * cur ) { if( cur -> l > r || cur -> r < l) return ; if( l <= cur-> l && cur -> r <= r ) { mark( w , cur ); return ; } register int mid = ( cur -> l + cur -> r ) >> 1; if( l <= mid ) modify( l , r , w , cur -> left ); if( mid + 1 <= r ) modify( l , r , w , cur -> right); cur -> value = cur -> left -> value + cur -> right -> value; return ; } int main() { n = read() , m = read(); root = build( 1 , n ); for( register int i = 1 ; i <= m ; i ++ ) { register int op = read(); if( !op ) { register int x = read() , y = read(); modify( x , y , 1 , root ); } else { register int x = read(); printf( "%d\n" , query( x , x , root ) ); } } return 0; } ``` # 0x44 分块 > 本节部分内容选自 [oi-wiki](<https://oi-wiki.org/ds/decompose/>) ## 简介其实，分块是一种思想，而不是一种数据结构。从 NOIP 到 NOI 到 IOI，各种难度的分块思想都有出现。通常的分块算法的复杂度带根号，或者其他奇怪的复杂度，而不是 $\log$ 。分块是一种很灵活的思想，几乎什么都能分块，并且不难实现。你想写出什么数据结构就有什么，缺点是渐进意义的复杂度不够好。当然，在 $n=10^5$ 时，由于常数小，跟线段树可能差不多。这不是建议你们用分块的意思，在 OI 中，可以作为一个备用方案，首选肯定是线段树等高级的数据结构。以下通过几个例子来介绍～ ## 区间和动机：线段树太难写？将序列分段，每段长度 $T$ ，那么一共有 $\frac{n}{T}$ 段。维护每一段的区间和。单点修改：显然。区间询问：会涉及一些完整的段，和最多两个段的一部分。完整段使用维护的信息，一部分暴力求。复杂度 $O(\frac{n}{T}+T)$ 。区间修改：同样涉及这些东西，使用打标记和暴力修改，同样的复杂度。当 $T=\sqrt{n}$ 时，复杂度 $O(\sqrt{n})$ 。 ## 区间和 2 上一个做法的复杂度是 $\Omega(1) , O(\sqrt{n})$ 。我们在这里介绍一种 $O(\sqrt{n}) - O(1)$ 的算法。为了 $O(1)$ 询问，我们可以维护各种前缀和。然而在有修改的情况下，不方便维护，只能维护单个块内的前缀和。以及整块作为一个单位的前缀和。每次修改 $O(T+\frac{n}{T})$ 。询问：涉及三部分，每部分都可以直接通过前缀和得到，时间复杂度 $O(1)$ 。 ## 对询问分块同样的问题，现在序列长度为 $n$ ，有 $m$ 个操作。如果操作数量比较少，我们可以把操作记下来，在询问的时候加上这些操作的影响。假设最多记录 $T$ 个操作，则修改 $O(1)$ ，询问 $O(T)$ 。 $T$ 个操作之后，重新计算前缀和， $O(n)$ 。总复杂度： $O(mT+n\frac{m}{T})$ 。 $T=\sqrt{n}$ 时，总复杂度 $O(m \sqrt{n})$ 。 ## [Loj 6277. 数列分块入门 1](<https://loj.ac/problem/6277>) 我们用以个类似懒惰标记的东西来维护，对于整块我们只修改标记，对于散块暴力修改即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 50005 , M = 250; int n , len , tot , a[N] , tag[M] , pos[N] , lef[M] , rig[M]; inline int read() { register int x = 0 , f = 1; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f; } inline void add( int l , int r , int val ) { if( pos[l] == pos[r] ) { for( register int i = l ; i <= r ; a[i] += val , i ++ ); return ; } for( register int i = l ; i <= rig[ pos[l] ] ; a[i] += val , i ++ ); for( register int i = r ; i >= lef[ pos[r] ] ; a[i] += val , i -- ); for( register int i = pos[l] + 1 ; i <= pos[r] - 1 ; tag[i] += val , i ++ ); return ; } int main() { n = read() , len = sqrt( 1.0 * n ) , tot = n / len + ( n % len ? 1 : 0 ); for( register int i = 1 ; i <= n ; a[i] = read() , pos[i] = ( i - 1 ) / len + 1 , i ++ ); for( register int i = 1 ; i <= tot ; lef[i] = ( i - 1 ) * len + 1 , rig[i] = i * len , i ++ ); for( register int i = 1 , opt , l , r , val ; i <= n ; i ++ ) { opt = read() , l = read() , r = read() , val = read(); if( opt ) printf( "%d\n" , a[r] + tag[ pos[r] ] ); else add( l , r , val ); } return 0; } ``` ## [Loj 6278. 数列分块入门 2](<https://loj.ac/problem/6278>) 开一个`vector`储存每一个块内的元素，然后排序如果修改包含当前整个块在不会改变块内元素的相对大小，只修改标记如果没有能够包含整个块，就暴力修改，然后重新排序即可查询时，对于散块直接暴力扫一遍，整块的话二分查找 ```cpp #include <bits/stdc++.h> #define L( x ) ( ( x - 1 ) * len + 1 ) #define R( x ) ( x * len ) #define pb( x ) push_back( x ) using namespace std; const int N = 50005 , M = 250; int n , a[N] , len , tag[M] , pos[N]; vector< int > group[M]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void reset( int x ) { group[x].clear(); for( register int i = L( x ) ; i <= R( x ) ; i ++ ) group[x].pb( a[i] ); sort( group[x].begin() , group[x].end() ); return ; } int query(int l,int r,int val) { register int res = 0 , p = pos[l] , q = pos[r]; if( p == q ) { for( register int i = l ; i <= r ; i ++ ) { if( a[i] + tag[p] < val ) res ++; } return res; } for( register int i = l ; i <= R( p ) ; i ++ ) { if( a[i] + tag[p] < val ) res ++; } for( register int i = r ; i >= L( q ) ; i -- ) { if( a[i] + tag[q] < val ) res ++; } for( register int i = p + 1 ; i <= q - 1 ; i ++ ) res += lower_bound( group[i].begin() , group[i].end() , val - tag[i] ) - group[i].begin(); return res; } inline void modify( int l , int r , int val ) { register int p = pos[l] , q = pos[r]; if( p == q ) { for( register int i = l ; i <= r ; a[i] += val , i ++ ); reset( p ); return ; } for( register int i = l ; i <= R( p ) ; a[i] += val , i ++ ); for( register int i = r ; i >= L( q ) ; a[i] += val , i -- ); reset( p ) , reset( q ); for( register int i = p + 1 ; i <= q - 1 ; tag[i] += val , i ++ ); return ; } int main() { n = read() , len = sqrt( 1.0 * n ); for( register int i = 1 ; i <= n ; a[i] = read() , group[ pos[i] = ( i - 1 ) / len + 1 ].pb( a[i] ) , i ++ ); for( register int i = 1 ; i <= pos[n] ; sort( group[i].begin() , group[i].end() ) , i ++ ); for( register int i = 1 , opt , l , r , val ; i <= n ; i ++ ) { opt = read() , l = read() , r = read() , val = read(); if( opt ) printf( "%d\n" , query( l , r , val * val ) ); else modify( l , r , val ); } return 0; } ``` 通过这两道，我们可以以总结下怎么思考一个分块 1. 不完整的块怎么处理 2. 完整的块怎么处理 3. 预处理什么信息 ## [Loj 6279. 数列分块入门 3](<https://loj.ac/problem/6279>) 这道题的做法和第二题比较类似分块，块内排序，二分查找，块外暴力扫对于这道题你会发现如果直接把分成$\sqrt{n}$块的话会$T$掉一部分点所以我们这这里引入均值不等式$\sqrt{xy} \le \frac{1}{2}(x+y)$，当且仅当$x=y$时，$\sqrt{xy} = \frac{1}{2}(x+y)$ 假设序列长度为$n$，块的大小为$x$，自然有$y=\frac{n}{x}$块，假设每次操作的复杂度为$Ax+By$ 则根据均值不等式可以得到$Ax+By \ge 2\sqrt{ABn} $ 所以可知 \]

Ax=By\Rightarrow x=\frac{By}{A}=\frac{Bn}{Ax}\Rightarrow x^2=\frac{B}{A}n\Rightarrow x=\sqrt{\frac{B}{A}n}

\[根据上面的推到可知当$x=\sqrt{\frac{B}{A}n}$时复杂度最低，最低为$O(2\sqrt{ABn})$ 对于本题每次操作是$O(x+log_ny)$的，自然可得$x=\sqrt{nlog_n}\approx 700$ 但是由于我们在计算复杂度时只考虑数量级，难免会有误差所以我们可以用两个仅仅时块的大小不一样的程序对拍，比较时间找出比较快的分块大小 ```cpp #include <bits/stdc++.h> #define L( x ) ( ( x - 1 ) * len + 1 ) #define R( x ) ( x * len ) using namespace std; const int N = 1e5+5 , M = 1e3 + 5 ,INF = - 1 << 31; int n , len , a[N] , pos[N] , tag[M]; set< int > group[M]; inline int read() { register int x = 0 , f = 1; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline int query( int l , int r , int val ) { register int res = -1 , p = pos[l] , q = pos[r]; if( p == q ) { for( register int i = l ; i <= r ; i ++ ) { if( a[i] + tag[ q ] < val ) res = max( res , a[i] + tag[ q ] ); } return ( res != INF ? res : - 1 ); } for( register int i = l ; i <= R( p ) ; i ++ ) { if( a[i] + tag[ p ] < val ) res = max( res , a[i] + tag[p] ); } for( register int i = r ; i >= L( q ) ; i -- ) { if( a[i] + tag[ q ] < val ) res = max( res , a[i] + tag[q] ); } for( register int i = p + 1 ; i <= q - 1 ; i ++ ) { auto t = group[i].lower_bound( val - tag[i] ); if( t == group[i].begin() ) continue; t -- ; res = max( res , *t + tag[i] ); } return res; } inline void modify( int l , int r , int val ) { register int p = pos[l] , q = pos[r]; if( p == q ) { for( register int i = l ; i <= r ; group[p].erase(a[i]) , a[i] += val , group[p].insert(a[i]) , i ++ ) ; return ; } for( register int i = l ; i <= R( p ) ; group[p].erase(a[i]) , a[i] += val , group[p].insert(a[i]) , i ++ ); for( register int i = r ; i >= L( q ) ; group[q].erase(a[i]) , a[i] += val , group[q].insert(a[i]) , i -- ); for( register int i = p + 1 ; i <= q - 1 ; tag[i] += val , i ++ ); return ; } int main() { n = read() , len = 1000; for( register int i = 1 ; i <= n ; a[i] = read() , pos[i] = ( i - 1 ) / len + 1 , group[ pos[i] ].insert( a[i] ) , i ++ ); for( register int i = 1 , opt , l , r , val ; i <= n ; i ++ ) { opt = read() , l = read() , r = read() , val = read(); if( opt )printf("%d\n" , query( l , r , val ) ); else modify( l , r , val ); } return 0; } ``` ## [P3372 【模板】线段树 1](<https://www.luogu.org/problem/P3372>) 没错，这是一道线段树模板题，但是不妨来用线段树做一下是可以的 ```cpp #include <bits/stdc++.h> #define LL long long #define L( x ) ( ( x - 1 ) * len + 1 ) #define R( x ) ( x * len ) using namespace std; const int N = 1e5 + 5 , M = 1e3 + 5 ; int n , m , len , tot , pos[N] , lef[M] , rig[M]; LL a[N] , sum[N] , tag[M]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline LL query( int l , int r ) { register LL res = 0; if( pos[l] == pos[r] )//如果在一个块中 { for( register int i = l ; i <= r ; res += a[i] + tag[ pos[i] ] , i ++ ); return res; } for( register int i = l ; i <= rig[ pos[l] ] ; res += a[i] + tag[ pos[i] ] , i ++ );//散块 for( register int i = r ; i >= lef[ pos[r] ] ; res += a[i] + tag[ pos[i] ] , i -- ); for( register int i = pos[l] + 1 ; i <= pos[r] - 1 ; res += sum[i] + tag[i] * ( rig[i] - lef[i] + 1 ) , i ++ );//整块 return res; } inline void modify( int l , int r , LL val ) { for( register int i = l ; i <= min( r , rig[ pos[l] ] ) ; a[i] += val , sum[ pos[i] ] += val , i ++ );//散块 for( register int i = r ; i >= max( l , lef[ pos[r] ] ) ; a[i] += val , sum[ pos[r] ] += val , i -- ); for( register int i = pos[l] + 1 ; i <= pos[r] - 1 ; tag[i] += val , i ++ );//整块 } int main() { n = read() , m = read(); len = sqrt( 1.0 * n ) , tot = n / len; if( n % len ) tot ++; for( register int i = 1 ; i <= n ; a[i] = read() , pos[i] = ( i - 1 ) / len + 1 , sum[ pos[i] ] += a[i] , i ++) for( register int i = 1 ; i <= tot ; lef[i] = ( i - 1 ) * len + 1 , rig[i] = i * len , i ++ ); for( register int opt , l , r , val ; m >= 1 ; m -- ) { opt = read() , l = read() , r = read(); if( opt & 1 ) val = read() , modify( l , r , val ); else printf( "%lld\n" , query( l , r ) ); } return 0; } ``` ![](https://cdn.luogu.com.cn/upload/image_hosting/z5q26hla.png) 请忽视我分块开了$O2$，可以注意到，分块不仅代码短而且跑得并不慢不过这道题貌似没有构造数据 # 0x51 线性DP ## LIS 最长上升子序列，给定一个长度为$N$序列$A$，求出数值单调递增的子序列长度最长是多少 ### $O(n^2)$做法 $f[i]$表示以$i$结尾的最长上升子序列长度是多少自然转移方程为$f[i]=max(f[j])+1,(1\le j < i,A[j]<A[i] )$ ```cpp for( register int i = 1 ; i <= n ; i ++ ) { f[i] = 1; for( register int j = 1 ; j < i ; j ++) { if( a[j] >= a[i] ) continue; f[i] = max( f[i] , f[j] + 1 ); } } ``` ### $O(nlog_n)$做法对于$O(n^2)$的做法，我们每次都枚举假设我们已经求的一个最长上升子序列，我们要进行转移，如果对于每一位，在不改变性质的情况下，每一位越小，后面的位接上去的可能就越大，所以对于每一位如果大于末尾一位，就把他接在末尾，否则在不改变性质的情况下，把他插入的序列中 ```cpp for( register int i = 1 ; i <= n ; i ++ ) { if( a[i] > f[ tot ] ) f[ ++ tot ] = a[i]; else *upper_bound( f + 1 , f + 1 + tot , a[i] ) = a[i]; } //tot就是LIS的长度 ``` 这种做法的缺点是不能求出每一位的$LIS$，注意最后的序列并不是$LIS$，只是长度是$LIS$的长度 ### 输出路径 $O(nlog_n)$的方法无法记录路径，所以考虑在$O(n^2)$的方法上进行修改，其实就是记录路径 ```cpp inline void output( int x )//递归输出 { if( x == from[x] ) { printf("%d " , a[x] ); return ; } output( from[x] ); printf("%d " , a[x] ); return ; } int main() { n = read(); for( register int i = 1 ; i <= n ; i ++ ) a[i] = read(); for( register int i = 1 ; i <= n ; i ++ ) { f[i] = 1 , from[i] = i; for( register int j = 1 ; j < i ; j ++ ) { if( a[j] >= a[i] || f[j] + 1 <= f[i] ) continue; f[i] = f[j] + 1; from[i] = j; } } for( register int i = 1 ; i <= n ; i ++ ) output( i ) , puts(""); //这中做法不仅可以得到路径，还可以得到每一个前缀的LIS的路径 return 0; } ``` ## LCS ## [Luogu P3902 递增](<https://www.luogu.org/problem/P3902>) 最长上升子序列问题的模板题，求出当前序列的最长上升子序列长度 ```cpp #include<bits/stdc++.h> using namespace std; const int N = 1e5 + 5; int n , a[N] , tot; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read(); for( register int i = 1 , x ; i <= n ; i ++ ) { x = read(); if( x > a[ tot ] ) a[ ++ tot ] = x; else * upper_bound( a + 1 , a + 1 + tot , x ) = x; } cout << n - tot << endl; } ``` 这里题目要求的是严格递增，如果要求递增可以把`upper_bound`换成`lower_bound` ## [AcWing 271. 杨老师的照相排列](<https://www.acwing.com/problem/content/273/>) 这道题的题面非常的绕其实就是让你放$1\cdots N$个数，每一行，每一列都是递增的显然放的顺序是没有影响的，那我们不妨从$1$到$N$逐个放首先先找一些性质 1. $1$一定放在$(1,1)$上，不然不能满足递增 2. 我们在放每一行的时候，必须要从左到右挨个放，显然在放$x$的时候，如果$x-1$没有放，那么在以后放$x-1$这个位置的数一定会比$x$更大 3. 我们在放$(i,j)$时，$(i+1,j)$一定不能放，同理也是无法满足递增有了这些性质我们就可以设计转移了我们用$f[a,b,c,d,e]$来表示地几行放了几个数如果`a && a - 1 >=b`，那么$f[a,b,c,d,e]$可以由$f[a-1,b,c,d,e]$转移来，即`f[a][b][c][d][e]+=f[a-1][b][c][d][e]` 同理如果`b && b - 1 >= c`，那么就有`f[a][b][c][d][e]+=f[a][b-1][c][d][e]` 同理可得其他三种情况 ```cpp #include <bits/stdc++.h> #define LL long long using namespace std; const int N = 35; int n , s[6]; LL f[N][N][N][N][N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { for( ; ; ) { n = read(); if( !n ) break; memset( s , 0 , sizeof( s ) ); for( register int i = 1 ; i <= n ; i ++ ) s[i] = read(); memset( f , 0 , sizeof( f ) ); f[0][0][0][0][0] = 1; for( register int a = 0 ; a <= s[1] ; a ++ ) { for( register int b = 0 ; b <= min( a , s[2] ) ; b ++ ) { for( register int c = 0 ; c<= min( b , s[3] ) ; c ++ ) { for( register int d = 0 ; d <= min( c , s[4] ) ; d ++ ) { for( register int e = 0 ; e <= min( d , s[5] ) ; e ++ ) { register LL &t = f[a][b][c][d][e]; if( a && a - 1 >= b ) t += f[ a - 1 ][b][c][d][e]; if( b && b - 1 >= c ) t += f[a][ b - 1 ][c][d][e]; if( c && c - 1 >= d ) t += f[a][b][ c - 1 ][d][e]; if( d && d - 1 >= e ) t += f[a][b][c][ d - 1 ][e]; if( e ) t += f[a][b][c][d][ e - 1 ]; } } } } } cout << f[ s[1] ][ s[2] ][ s[3] ][ s[4] ][ s[5] ] << endl; } return 0; } ``` ## [AcWing 272. 最长公共上升子序列](<https://www.acwing.com/problem/content/274/>) 设计状态转移方程 `f[i][j]`表示$a[1\cdots i]$和$b[1\cdots j]$中以$b[j]$为结尾的最长公共子序列那么就可以得到 \]

f[i][j]=\left{ \begin{matrix} f[i-1][j]，(a[i]!= b[j])\max(f[i-1][1\le k < j]),(a[i]==b[j] ,a[i]>b[k]) \end{matrix}\right.

\[那么这个算法的实现就很简单 ```cpp for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = 1 ; j <= n ; j ++ ) { f[i][j] = f[i-1][j]; if( a[i] == a[j] ) { register int maxv = 1; for( register int k = 1 ; k < j ; k ++ ) if( a[i] > b[k] ) maxv = max( maxv , f[ i - 1 ][k] ); f[i][j] = max( f[i][j] , maxv + 1 ); } } } ``` 然后我们发现`maxv`的值与`i`无关，只与`j`有关所以我们可以吧求`maxv`过程提出来，这样复杂度就降到了$O(n^2)$ ```cpp #include <bits/stdc++.h> using namespace std; const int N = 3010; int n , a[N] , b[N] , f[N][N]; inline int read() { register int x = 0 , f = 1; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f ; } int main() { n = read(); for( register int i = 1 ; i <= n ; i ++ ) a[i] = read(); for( register int i = 1 ; i <= n ; i ++ ) b[i] = read(); for( register int i = 1 , maxv ; i <= n ; i ++ ) { maxv = 1; for( register int j = 1 ; j <= n ; j ++ ) { f[i][j] = f[ i - 1 ][j]; if( a[i] == b[j] ) f[i][j] = max( f[i][j] , maxv ); if( a[i] > b[j] ) maxv = max( maxv , f[ i - 1 ][ j ] + 1 ); } } register int res = -1; for( register int i = 1 ; i <= n ; i ++ ) res = max( res , f[n][i] ); cout << res << endl; } ``` ## [AcWing 273. 分级 ](<https://www.acwing.com/problem/content/description/275/>) 对于单调递增和单调递减的情况我们分别求一下，取较小值即可这里只考虑单调递增的情况先来一个引理 > 一定存在一组最优解，使得$B_i$中的每个元素都是$A_i$中的某一个值证明如下 ![](https://cdn.acwing.com/media/article/image/2019/10/01/1_861faab8e3-acwing_273.png) 横坐标$A_i$表示原序列，$A`_i$表示排序后的序列，红色圈代表$B_i$ 粉色框里框住的圈，是$B_i$不是$A_i$中某个元素的情况，当前状态是一个解我们统计出$A_2\cdots A_4$中大于$A`_1$的个数$x$和小于$A`_1$的个数$y$ 如果$x>y$，我们将框内的元素向上平移，直到最高的一个碰到$A`_2$，结果会变得更优如果$x<y$，我们将框内的元素向下平移，直到最高的一个碰到$A`_1$，结果会变得更优如果$x=y$，向上向下都可以，结果不会变差我们可以通过这种方式得到一组符合引里的解换言之我们只要从$A_i$找到一个最优顺序即可那么考虑状态转移方程 `f[i][j]`表示长度为`i`且`B[i]=A'[j]`的最小值考虑`B[i-1]`的范围是`A'[1]~A[j]`，所以`f[i][j]=min(f[i-1][1~j])+abs(A[i]-B[j])` 为什么这里可以取到`j`呢，注意题目上说的是非严格单调的，所以`B[i]==B[i-1]`是合法的 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 2005 , INF = 0x7f7f7f7f; int n , a[N] , b[N] , f[N][N] , res; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline int work() { for( register int i = 1 , minv = INF ; i <= n ; i ++ , minv = INF ) { for( register int j = 1 ; j <= n ; j ++ ) { minv = min( minv , f[ i - 1 ][j] ); f[i][j] = minv + abs( a[i] - b[j] ); } } register int ans = INF; for( register int i = 1 ; i <= n ; i ++ ) ans = min( ans , f[n][i] ); return ans; } int main() { n = read(); for( register int i = 1 ; i <= n ; i ++ ) a[i] = b[i] = read(); sort( b + 1 , b + 1 + n ); res = work(); reverse( a + 1 , a + 1 + n ); printf( "%d\n" , min( res , work() ) ); return 0; } ``` ## [AcWing 274. 移动服务](<https://www.acwing.com/problem/content/276/>) 当我们看到的题目的第一反应是设状态方程`f[x][y][z]`表示三个人分别在`x,y,z`上但是我们发现我们并不知道最终的状态是是什么，因为只知道有一个人在`p[n]`上其他的都不知道，所以更换思路我们设`f[i][x][y]`表示三个人分别在`p[i],x,y`位置上，这样最终状态就是`f[n][x][y]`我们只要找到最小的一个即可转移很简单就是枚举三个人从`p[i]`走到`p[i+1]`即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 1005 , M = 205 , INF = 0x7f7f7f7f; int n , m , dis[M][M] , q[N] , f[N][M][M] , res = INF; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { m = read() , n = read(); for( register int i = 1 ; i <= m ; i ++ ) { for( register int j = 1 ; j <= m ; j ++ ) dis[i][j] = read(); } for( register int i = 1 ; i <= n ; i ++ ) q[i] = read(); q[0] = 3; memset( f , INF , sizeof( f ) ) , f[0][1][2] = 0; for( register int i = 0 ; i < n ; i ++ ) { for( register int x = 1 ; x <= m ; x ++ ) { for( register int y = 1 ; y <= m ; y ++ ) { register int z = q[i] , v = f[i][x][y]; if( x == y || z == x || z == y ) continue; register int u = q[ i + 1 ]; f[ i + 1 ][x][y] = min( f[ i + 1 ][x][y] , v + dis[z][u] ); f[ i + 1 ][z][y] = min( f[ i + 1 ][z][y] , v + dis[x][u] ); f[ i + 1 ][x][z] = min( f[ i + 1 ][x][z] , v + dis[y][u] ); } } } for( register int i = 1 ; i <= m ; i ++ ) { for( register int j = 1 ; j <= m ; j ++ ) { if( i == j || i == q[n] || j == q[n] ) continue; res = min( res , f[n][i][j] ); } } cout << res << endl; return 0; } ``` 到这里已经可以过这道题了我们考虑还能怎么优化，显然时间复杂度很难优化了，下面介绍一个常用的东西 ## 滚动数组优化动态规划空间复杂度我们发现整个`DP`状态转移中，能够影响`f[i+1][x][y]`的只有`f[i][x][y]`所以我们没有必要存`f[i-1][x][y]`之前的状态所以只保存两个状态即可我们用两个值`to`和`now`来表示状态的下标，每次转移后交换两个值即可，这样可以减少大部分的空间 ```cpp #include <bits/stdc++.h> #define exmin( a , b , c , d ) ( min( min( a , b ) , min( c , d ) ) ) using namespace std; const int N = 1005 , M = 205 , INF = 0x7f7f7f7f; int n , m , dis[M][M] , q[N] , f[2][M][M] , res = INF , to , now; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { m = read() , n = read(); for( register int i = 1 ; i <= m ; i ++ ) { for( register int j = 1 ; j <= m ; j ++ ) dis[i][j] = read(); } for( register int i = 1 ; i <= n ; i ++ ) q[i] = read(); q[0] = 3; now = 0 , to = 1 ; memset( f[now] , INF , sizeof( f[now] ) ); f[now][1][2] = 0; for( register int i = 0 ; i < n ; i ++ ) { memset( f[to] , INF , sizeof( f[to] ) ); for( register int x = 1 ; x <= m ; x ++ ) { for( register int y = 1 ; y <= m ; y ++ ) { register int z = q[i] , v = f[now][x][y]; if( x == y || z == x || z == y ) continue; register int u = q[ i + 1 ]; f[ to ][x][y] = min( f[ to ][x][y] , v + dis[z][u] ); f[ to ][z][y] = min( f[ to ][z][y] , v + dis[x][u] ); f[ to ][x][z] = min( f[ to ][x][z] , v + dis[y][u] ); } } swap( to , now ); } for( register int i = 1 ; i <= m ; i ++ ) { for( register int j = 1 ; j <= m ; j ++ ) { if( i == j || i == q[n] || j == q[n] ) continue; res = min( res , f[now][i][j] ); } } cout << res << endl; return 0; } ``` # 0x52 背包问题 ## 0/1背包给定$N$个物品，其中第$i$个物品的体积为$V_i$，价值为$W_i$。有一个容积为$M$的背包，要求选择一些物品放入背包，在体积不超过$M$的情况下，最大的价值总和是多少我们设`f[i][j]`表示前`i`个物品用了`j`个空间能获得的最大价值，显然可以得到下面的转移 ```cpp int f[N][M]; for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = v[i] ; j <= m ; j ++ ) { f[i][j] = f[ i - 1 ][j]; f[i][j] = max( f[i][j] , f[ i - 1 ][ j - v[i] ] + w[i] ); } } int ans = 0; for( register int i = 0 ; i <= m ; i ++ ) ans = max( ans , f[n][i] ); ``` 显然可以用滚动数组优化空间，得到下面的代码 ```cpp int f[2][M]; for( register int i = 1 ; i i <= n ; i ++ ) { for( register int j = v[i] ; j <= m ; j ++ ) { f[ i & 1 ][j] = f[ ( i - 1 ) & 1 ][j]; f[ i & 1 ][j] = max( f[ i & 1 ][j] , f[ ( i - 1 ) & 1 ][ j - v[i] ] + w[i] ); } } int ans = 0; for( register int i = 0 ; i <= m ; i ++ ) ans = max( ans , f[ n & 1 ][i] ); ``` 当这并不是常规的写法，下面这种才是常规的写法 ```cpp int f[M]; for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = m ; j >= v[i] ; j -- ) { f[j] = max( f[j] , f[ j - v[i] ] + w[i] ); } } int ans = 0; for( register int i = 0 ; i <= m ; i ++ ) ans = max( ans , f[i] ); ``` 但是我们发现在枚举空间的时候是倒序枚举，是为了防止多次重复的选择导致不合法举个例子你先选到`f[v[i]]`会选择一次物品`i`，但当选择到`f[2*v[i]]`时就会再选择一次，显然是不合法的所以要记住$0/1$背包的这一重点，要倒序枚举空间 ## [AcWing 278. 数字组合](<https://www.acwing.com/problem/content/280/>) 按照$0/1$背包的模型求解方案数即可 ```cpp int main() { n = read() , m = read() , f[0] = 1; for( register int i = 1 , v ; i <= n ; i ++ ) { v = read(); for( register int j = m ; j >= v ; j -- ) f[j] += f[ j - v ]; } cout << f[m] << endl; return 0; } ``` ## [Luogu P1510 精卫填海](<https://www.luogu.org/problem/P1510>) 这也是一个经典的背包问题，背包求最小费用 `f[i][j]`表示前$i$个物品用了$j$的体力所能填满的最大空间，显然滚动数组优化一维空间然后枚举一下体力，找到最先填满全部体积的一个即可简单分析一下，当花费的体力增加时，所填满的体积保证不会减小，满足单调性二分查找会更快 ```cpp #include<bits/stdc++.h> using namespace std; const int N = 10005; int n , V , power ,f[N] , use; bool flag = 0; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { V = read() , n = read() , power = read(); for( register int i = 1 , v , w ; i <= n ; i ++ ) { v = read() , w = read(); for( register int j = power ; j >= w ; j -- ) f[j] = max( f[j] , f[ j - w ] + v ); } use = lower_bound( f + 1 , f + 1 + power , V ) - f; if( f[use] >= V ) printf( "%d\n" , power - use ); else puts("Impossible"); return 0; } ``` ## [Luogu P1466 集合 Subset Sums](<https://www.luogu.org/problem/P1466>) 结合一点数学知识，$\sum_{x=1}^xx=\frac{(x+1)x}{2}$ 要把这些数字平均分成两部分，那么两部分的和一定是$\frac{(x+1)x}{4}$ 剩下就是一个简单的背包计数模板 ```cpp #include<bits/stdc++.h> #define LL long long using namespace std; const int N = 400; LL n , m , f[N]; int main() { cin >> n; if( n * ( n + 1) % 4 ) { puts("0"); exit(0); } m = n * ( n + 1 ) / 4; f[0] = 1; for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = m ; j >= i ; j -- ) f[j] += f[ j - i ]; } cout << f[m] / 2 << endl; } ``` ## 完全背包给定$N$种物品，其中第$i$个物品的体积为$V_i$，价值为$W_i$，每个物品有无数个。有一个容积为$M$的背包，要求选择一些物品放入背包，在体积不超过$M$的情况下，最大的价值总和是多少这里你会发现完全背包和$0/1$背包的差别就只剩下数量了，所以代码也基本相同，只要把枚举容量改成正序循环即可 ```cpp int f[M]; for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = v[i] ; j <= m ; j ++ ) { f[j] = max( f[j] , f[ j - v[i] ] + w[i] ); } } int ans = 0; for( register int i = 0 ; i <= m ; i ++ ) ans = max( ans , f[i] ); ``` ## [AcWing 279. 自然数拆分](<https://www.acwing.com/problem/content/281/>) 直接套用完全背包的模板并将`max`函数改成求和即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 4005; unsigned int n , f[N]; int main() { cin >> n; f[0] = 1; for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = i ; j <= n ; j ++ ) { f[j] = ( f[j] + f[ j - i ] ) % 2147483648u; } } cout << ( f[n] > 0 ? f[ n ] - 1 : 2147483648u ) << endl; return 0; } ``` ## [P2918 买干草Buying Hay](<https://www.luogu.org/problem/P2918>) 类似`P1510`精卫填海，不过这是完全背包稍作修该即可不过要注意`f[need]`并非最优解，因为可以多买点，只要比需要的多即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 505005 , INF = 0x7f7f7f7f; int n , need , f[N] , ans = INF ; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read() , need = read(); memset( f , INF , sizeof(f) ) , f[0] = 0; for( register int i = 1 , w , v ; i <= n ; i ++ ) { v = read() , w = read(); for( register int j = v ; j <= need + 5000; j ++ ) f[j] = min( f[j] , f[ j - v ] + w ) ; } for( register int i = need ; i <= need + 5000 ; i ++ ) ans = min( ans , f[i] ); cout << ans << endl; return 0; } ``` ## 多重背包给定$N$种物品，其中第$i$个物品的体积为$V_i$，价值为$W_i$，每个物品有$K_I$个。有一个容积为$M$的背包，要求选择一些物品放入背包，在体积不超过$M$的情况下，最大的价值总和是多少这里的多重背包还是对物品的数量进行了新的限制，限制数量，其实做法和$0/1$背包差不多，只要增加一维枚举数量即可 ## 二进制拆分优化众所周知，我们可以用$2^0,2^1,2^2\cdots,2^{k-1}$,这$k$个数中任选一些数相加构造出$1\cdots 2^k-1$中的任何一个数所以我们就可以把多个物品拆分成多种物品，做$0/1$背包即可二进制拆分的过程 ```cpp for( register int i = 1 , wi , vi , ki , p ; i <= n ; i ++ ) { wi = read() , vi = read() , ki = read() , p = 1; while( ki > p ) ki -= p , v[ ++ tot ] = vi * p , w[ tot ] = wi * p , p <<= 1; if( ki > 0 ) v[ ++ tot ] = vi * ki , w[ tot ] = wi * ki; } ``` ## [Luogu P1776 宝物筛选](<https://www.luogu.org/problem/P1776>) 这是一道，经典的模板题，直接套板子即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 12e5 + 5; int n , m , v[N] , w[N] , f[N] , tot ; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read() , m = read(); for( register int i = 1 , vi , ki , wi , p ; i <= n ; i ++ ) { wi = read() , vi = read() , ki = read() , p = 1; while( ki > p ) ki -= p , w[ ++ tot ] = wi * p , v[tot] = vi * p , p <<= 1 ; if( ki ) w[ ++ tot ] = wi * ki , v[tot] = vi * ki; } for( register int i = 1 ; i <= tot ; i ++ ) { for( register int j = m ; j >= v[i] ; j -- ) f[j] = max( f[j] , f[ j - v[i] ] + w[i] ); } cout << f[m] << endl; return 0; } ``` ## 分组背包给定$N$组物品，每组内有多个不同的物品，每组的物品只能挑选一个。在背包容积确定的情况下求最大价值总和其实是$0/1$背包的一种变形，结合伪代码理解即可 ```cpp for( i /*枚举组*/) { for( j /*枚举容积*/) { for(k/*枚举组内物品*/) { f[j] = max( f[j] , f[ j - v[i][k] ] + w[i][k] ); } } } ``` 记住一定要先枚举空间这样可以保证每组物品只选一个 ## [Luogu P1757 通天之分组背包](<https://www.luogu.org/problem/P1757>) 模板题，套板子即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 1005 , M = 105; int n , m , v[N] , w[N] , f[N] , tot = 0; vector< int > g[M]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { m = read() , n = read(); for( register int i = 1 , a , b , c ; i <= n ; i ++ ) { v[i] = read() , w[i] = read() , c = read(); g[c].push_back( i ); tot = max( tot , c ); } for( register int i = 1 ; i <= tot ; i ++ ) { for( register int j = m ; j >= 0 ; j -- ) { for( auto it : g[i] ) { if( j < v[it] ) continue; f[j] = max( f[j] , f[ j - v[it] ] + w[it] ); } } } cout << f[m] << endl; return 0; } ``` ## 混合背包混合背包其实，一部分是$0/1$背包，完全背包，多重背包混合 ```cpp for ( /*循环物品种类*/ ) { if (/*是 0 - 1 背包*/ ) /* 套用 0 - 1 背包代码*/; else if ( /*是完全背包*/) /*套用完全背包代码*/; else if (/*是多重背包*/) /*套用多重背包代码*/; } ``` 有一种做法是利用二进制拆分全部转发成$0/1$背包来做，如果完全背包，就通过考虑上限的方式进行拆分，因为背包的容积是有限的，根据容积计算出最多能取多少个如果只有$0/1$背包和完全背包可以判断一下，$0/1$背包倒着循环，完全背包正着循环 ## [Luogu P1833 樱花](<https://www.luogu.org/problem/P1833>) # 0x53 区间DP 区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来由很大的关系。令状态表示将下标位置到的所有元素合并能获得的价值的最大值，那么，为将这两组元素合并起来的代价。区间 DP 的特点： **合并** ：即将两个或多个部分进行整合，当然也可以反过来； **特征** ：能将问题分解为能两两合并的形式； **求解** ：对整个问题设最优值，枚举合并点，将问题分解为左右两个部分，最后合并两个部分的最优值得到原问题的最优值。 ## [AcWing 282. 石子合并](<https://www.acwing.com/problem/content/284/>) `f[l][r]`表示将$l\cdots r $ 的石子合并成一堆所需要的最小代价因为每次只能合并两堆石子，所以我们可以枚举两堆石子的分界点，这应该是区间$DP$最简单的一道题了吧 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 305 , INF = 0x7f7f7f7f; int n , a[N] , s[N] , f[N][N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read(); for( register int i = 1 ; i <= n ; a[i] = read() , s[i] = s[ i - 1 ] + a[i] , i ++ ); for( register int len = 2 ; len <= n ; len ++ ) { for( register int l = 1 , r = len ; r <= n ; l ++ , r ++ ) { f[l][r] = INF; for( register int k = l ; k < r; k ++ ) f[l][r] = min( f[l][r] , f[l][k] + f[k+1][r] + s[r] - s[ l - 1 ] ); } } cout << f[1][n] << endl; return 0; } ``` ## [Luogu P4170 涂色](<https://www.luogu.org/problem/P4170>) 设`f[l][r]`为将`l`到`r`全部涂成目标状态的最下代价显然当`l == r`时，`f[l][r] = 1` 当`l != r`且`opt[l] == opt[r]`时，只需在涂抹中间区间时多涂抹一格，即`f[l][r] = min( f[l+1][r] , f[l][r-1 ] )` 当`l != r`且`opt[l] != opt[r]`时，考虑分成两个区间来涂抹，即`f[l][r]=min( f[l][k] + f[k+1][r] )` 设计好状态转移后，按照套路枚举区间长度，枚举左端点，转移即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 55 , INF = 0x7f7f7f7f; int n , f[N][N]; string opt; int main() { cin >> opt; n = opt.size(); for( register int i = 1 ; i <= n ; i ++ ) f[i][i] = 1; for( register int len = 2 ; len <= n ; len ++ ) { for( register int l = 1 , r = len ; r <= n ; l ++ , r ++ ) { if( opt[ l - 1 ] == opt[ r - 1 ] ) f[l][r] = min( f[ l + 1 ][r] , f[l][ r - 1 ] ); else { f[l][r] = INF; for( register int k = l ; k < r ; k ++ ) f[l][r] = min( f[l][r] , f[l][k] + f[ k + 1 ][r] ); } } } cout << f[1][n] << endl; return 0; } ``` ## [Luogu P3205 合唱队](<https://www.luogu.org/problem/P3205>) `f[l][r][0/1]`表示站成目标队列`l`到`r`部分，且最后一个人在左或右边的方案数根据题目的要求稍作思考就能得到转移方程 ```cpp f[l][r][0] = f[ l + 1 ][r][0] * ( h[l] < h[ l + 1 ] ) + f[ l + 1 ][r][1] * ( h[l] < h[r] ) ; f[l][r][1] = f[l][ r - 1 ][0] * ( h[r] > h[l] ) + f[l][ r - 1 ][1] * ( h[r] > h[ r - 1 ] ) ; ``` ```cpp #include<bits/stdc++.h> using namespace std; const int N = 1005 , mod = 19650827; int n , h[N] , f[N][N][2]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read(); for( register int i = 1 ; i <= n ; h[i] = read() , f[i][i][0] = 1 , i ++ ); for( register int len = 2 ; len <= n ; len ++ ) { for( register int l = 1 , r = len ; r <= n ; l ++ , r ++ ) { f[l][r][0] = ( f[ l + 1 ][r][0] * ( h[l] < h[ l + 1 ] ) + f[ l + 1 ][r][1] * ( h[l] < h[r] ) ) % mod; f[l][r][1] = ( f[l][ r - 1 ][0] * ( h[r] > h[l] ) + f[l][ r - 1 ][1] * ( h[r] > h[ r - 1 ] ) ) % mod; } } cout << ( f[1][n][0] + f[1][n][1] ) % mod << endl; return 0; } ``` ## [Loj 10148. 能量项链](<https://loj.ac/problem/10148>) 这道题因为是环，直接处理很复杂，用到一个常用的技巧**破环成链** 简单说就是把环首未相接存两边，剩下的就是区间$DP$了模板了 ```cpp #include<bits/stdc++.h> using namespace std; const int N = 205; int n , head[N] , tail[N] , f[N][N] , ans; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read(); for( register int i = 1 ; i <= n ; head[i] = head[ i + n ] = read() , i ++ ); for( register int i = 1 ; i < 2 * n ; tail[i] = head[ i + 1 ] , f[i][i] = 0 , i ++ ); tail[ n * 2 ] = head[1]; for( register int len = 2 ; len <= n ; len ++ ) { for( register int l = 1 , r = len ; r < n * 2 ; l ++ , r ++ ) { for( register int k = l ; k < r ; k ++ ) f[l][r] = max( f[l][r] , f[l][k] + f[ k + 1][r] + head[l] * tail[k] * tail[r] ); if( len == n ) ans = max( ans , f[l][r] ); } } cout << ans << endl; return 0; } ``` 说到破环成链，前面的石子合并其实也是要破环成链的，但数据太水了，[Loj 10147.石子合并](<https://loj.ac/problem/10147>)题目不变当数据比上面加强了，需要考虑破环成链 # 0x54 树形DP 树形$DP$，即在树上进行的$DP$。由于树固有的递归性质，树形$DP$一般都是递归进行的。 ## [Luogu P1352 没有上司的舞会](<https://www.luogu.org/problem/P1352>) 定义`f[i][0/1]`$表示以$i$为根节点是否选择$i$的最有解显然可以得到下面的转移方程，其中`v`表示`i`的子节点 `f[i][1] += f[v][0] ` `f[i][0] += max( f[v][1] , f[v][0] ) ` 然后我们发现这样似乎很难递推做，所以大多数时候的树形$DP$都是用$DFS$来实现的 ```cpp #include <bits/stdc++.h> #define PII pair< int , int > #define v first #define next second using namespace std; const int N = 6005; int n , w[N] , root , head[N] , tot , f[N][2]; bool st[N]; PII e[N]; inline int read() { register int x = 0 , f = 1 ; register char ch = getchar(); while( ch < '0' || ch > '9') { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 1 ) + ( x << 3 ) + ch - '0'; ch = getchar(); } return x * f; } inline void add( int u , int v ) { e[++tot] = { v , head[u] } , head[u] = tot; } inline void dfs( int u ) { f[u][1] = w[u]; for( register int i = head[u] ; i ; i = e[i].next ) { dfs( e[i].v ); f[u][0] += max( f[ e[i].v ][1] , f[ e[i].v ][0] ); f[u][1] += f[ e[i].v ][0]; } return ; } int main() { n = read(); for( register int i = 1 ; i <= n ; w[i] = read() , i ++ ); for( register int i = 1 , u , v ; i < n ; i ++ ) { v = read() , u = read(); add( u , v ) , st[v] = 1; } for( root = 1 ; st[root] ; root ++ ); dfs( root ); cout << max( f[root][1] , f[root][0] ) << endl; return 0; } ``` ## [AcWing 286. 选课](<https://www.acwing.com/problem/content/288/>) 这是一道依赖条件的背包，可以当作是在树上做背包因为每个子树之间没有横插边，所以每个子树是相互独立的所以当前节点的最大值就是子树最大值之和加当前节点的权值我们给任意一个子树分配任意的空间，不过每个子树只能用一次，所以这里用到呢分组背包的处理原图不保证是一颗树，所以可能是一个森林，建立一个虚拟节点，权值为$0$和每个子树的根节点相连，这样就构成一颗完整的树，这里把$0$当作了虚拟节点 ```cpp #include <bits/stdc++.h> #define PII pair< int , int > #define v first #define next second #define son e[i].v using namespace std; const int N = 305; int n , m , w[N] , head[N] , tot = 0, f[N][N]; PII e[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int u , int v ) { e[ ++ tot ] = { v , head[u] } , head[u] = tot; return ; } inline void dfs( int u ) { for( register int i = head[u] ; i != -1 ; i = e[i].next ) { dfs( son ); for( register int j = m - 1 ; j >= 0 ; j -- ) { for( register int k = 1 ; k <= j ; k ++ ) { f[u][j] = max( f[u][j] , f[u][ j - k ] + f[ son ][ k ] ); } } } for( register int j = m ; j ; j -- ) f[u][j] = f[u][ j - 1 ] + w[u]; f[u][0] = 0; return ; } int main() { n = read() , m = read(); memset( head , -1 , sizeof( head ) ); for( register int i = 1 , u ; i <= n ; i ++ ) { u = read() , w[i] = read(); add( u , i ); } m ++; dfs(0); cout << f[0][m] << endl; return 0; } ``` ## [Luogu P1122 最大子树和](<https://www.luogu.org/problem/P1122>) 这道题的思路类似最大子段和，只不过是在树上做而已题目给的是以棵无根树，但在这道题没有什么影响我们以$1$来做整棵树的根节点，然后$f[i]$表示以$i$为根的子树的最大子树和每次递归操作，先计算出子树的权值在贪心的选择即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 16005 , INF = 0x7f7f7f7f; int n , v[N] , head[N] ,f[N] , ans; vector<int> e[N]; bool vis[N]; inline int read() { register int x = 0 , f = 1; register char ch = getchar(); while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); } while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x * f; } inline void dfs( int x ) { f[x] = v[x] , vis[x] = 1; for( register auto it : e[x] ) { if( vis[it] ) continue; dfs( it ); f[x] = max( f[x] , f[x] + f[it] ); } return ; } int main() { n = read(); for( register int i = 1 ; i <= n ; v[i] = read() , i ++ ); for( register int i = 1 , u , v ; i < n ; i ++ ) { u = read() , v = read(); e[u].push_back(v) , e[v].push_back(u); } dfs( 1 ); ans = -INF; for( register int i = 1 ; i <= n ; i ++ ) ans = max( ans , f[i] ); cout << ans << endl; return 0; } ``` ## [Luogu P2016 战略游戏](<https://www.luogu.org/problem/P2016>) `f[i][0/1]`表示节点`i`选或不选所需要的最小代价如果当前的节点选，子节点选不选都可以如果当前节点不选，每一个子节点都必须选，不然无法保证每条边都被点亮递归计算子节点在根据这个原则进行转移即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 1505; int n , f[N][2]; bool vis[N]; vector< int >e[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void dfs( int x , int fa ) { vis[x] = 1; f[x][1] = 1; for( register auto it : e[x] ) { if( it == fa ) continue; dfs( it , x ); f[x][0] += f[it][1]; f[x][1] += min( f[it][1] , f[it][0] ); } return ; } int main() { n = read(); for( register int i = 1 , u , v , k ; i <= n ; i ++ ) { for( u = read() + 1 , k = read() ; k >= 1 ; v = read() + 1 , e[u].push_back(v) , e[v].push_back(u) , k -- ); } dfs( 1 , -1 ); cout << min( f[1][0] , f[1][1] ) << endl; return 0; } ``` ## [Luogu P2458 保安站岗](<https://www.luogu.org/problem/P2458>) 这道题和上一道比较类似，但这道题他是要覆盖每一个点而不是每一个边设`f[i][0/1/2]`表示第`i`个点被自己、儿子、父亲所覆盖且子树被全部覆盖，所需要的最小代价如果被自己覆盖，则儿子的状态可以是任意状态，所以`f[u][0] += min( f[v][0] , f[v][1] , f[v][2] )` 如果被父亲覆盖，则儿子必须被自己或孙子覆盖，所以`f[u][2] += min( f[v][0] , f[v][1] )` 如果被儿子覆盖，只需有一个儿子覆盖即可，其他的随意，所以`f[u][1] += min( f[v][0] , f[v][1] )` 但要特判一下如果所有的儿子都是被孙子覆盖比自己覆盖自己更优的话为了保证合法就要加上`min( f[v][0] - f[v][1])` 递归操作根据上述规则转移即可 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 1500 , INF = 1e9+7; int n , w[N] , f[N][3]; //f[i][0/1/2] 分别表示 i 被自己/儿子/父亲覆盖 vector< int > e[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x ; } inline void add( int u , int v ) { e[u].push_back( v ) , e[v].push_back( u ); } inline void dfs( int x , int fa ) { f[x][0] = w[x]; register int cur , cnt = INF; register bool flag = 0; for( auto it : e[x] ) { if( it == fa ) continue; dfs( it , x ); cur = min( f[it][0] , f[it][1] ); f[x][0] += min( cur , f[it][2] );//当前点已经选择，儿子无所谓 f[x][2] += cur; // 当前点被父亲覆盖，儿子必须覆盖自己或被孙子覆盖 if( f[it][0] < f[it][1] || flag ) flag = 1;// 如果有选择一个儿子，比儿子被孙子覆更优，做标记 else cnt = min( cnt , f[it][0] - f[it][1] ); f[x][1] += cur; } if( ! flag ) f[x][1] += cnt;//如果全部都选择儿子被孙子覆盖，则强制保证合法 } int main() { n = read(); for( register int i = 1 , u , k , v ; i <= n ; i ++ ) { u = read() , w[u] = read() , k = read(); for( ; k >= 1 ; v = read() , add( u , v ) , k -- ); } dfs( 1 , 0 ); cout << min( f[1][0] , f[1][1] ) << endl; return 0; } ``` ## [Luogu P1273 有线电视网](<https://www.luogu.org/problem/P1273>) 树上分组背包，其实做起来的过程类似普通的分组背包 `f[i][j]`表示对于节点`i`，满足前`j`个儿子的最大权值然后就是枚举一下转移就好 ```cpp #include<bits/stdc++.h> #define PII pair< int , int > #define v first #define w second using namespace std; const int N = 3005 , INF = 0x7f7f7f7f; int n , m , pay[N] , f[N][N]; vector< PII > e[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline int dfs( int x ) { if( x > n - m ) { f[x][1] = pay[x]; return 1; } register int sum = 0 , t ;// sum 当前节点子树有多少个点 , t 子节点子树有多少点 for( register auto it : e[x] ) { t = dfs( it.v ) , sum += t; for( register int j = sum ; j > 0 ; j -- ) { for( register int i = 1 ; i <= t && j - i >= 0 ; i ++ ) { f[x][j] = max( f[x][j] , f[x][ j - i ] + f[ it.v ][i] - it.w ); } } } return sum; } int main() { n = read() , m = read(); for( register int i = 1 , k , x , y ; i <= n - m ; i ++ ) { for( k = read() ; k >= 1 ; x = read() , y = read() , e[i].push_back( { x , y } ) , k -- ); } for( register int i = n - m + 1 ; i <= n ; pay[i] = read() , i ++ ); memset( f , - INF , sizeof( f ) ); for( register int i = 1 ; i <= n ; f[i][0] = 0 , i ++ ); dfs( 1 ); for( register int i = m ; i >= 1 ; i -- ) { if( f[1][i] < 0 ) continue; cout << i << endl; break; } return 0; } ``` ## [Luogu U93962 Dove 爱旅游](<https://www.luogu.org/problem/U93962>) 原图是一张黑白染色的图，我们在存权值时$1$还是$1$，$0$就当成$-1$来存设$f[i]$表示白色减黑色的最大值，$g[i]$表示黑色减白色的最大值，递归求解分别转移即可自己可以看代码理解下 ```cpp #include<bits/stdc++.h> #define exmax( a , b , c ) ( a = max( a , max( b , c ) ) ) using namespace std; const int N = 1e6 + 5; int n , a[N] , f[N] , g[N] , ans; vector< int > e[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void dfs( int u , int fa ) { g[u] = f[u] = a[u]; for( auto v : e[u] ) { if( v == fa ) continue; dfs( v , u ); f[u] += max( 0 , f[v] ); g[u] += min( 0 , g[v] ); } } int main() { n = read(); for( register int i = 1 ; i <= n ; i ++ ) a[i] = ( !read() ? -1 : 1 ); for( register int i = 1 , x , y ; i < n ; x = read() , y = read() , e[x].push_back(y) , e[y].push_back(x) , i ++ ); dfs( 1 , 0 ); for( register int i = 1 ; i <= n ; exmax( ans , f[i] , -g[i] ) , i ++ ); cout << ans << endl; return 0; } ``` ## [Loj #10153. 二叉苹果树](<https://loj.ac/problem/10153>) [Luogu P2015 二叉苹果树](<https://www.luogu.org/problem/P2015>) `f[i][j]`表示第`i`个点保留`j`个节点最大权值假如左子树保留`k`个节点，则右子树要保留`j-k-1`个节点，因为节点`i`也必须保存枚举空间`k`，去最大值即可 ```cpp #include<bits/stdc++.h> #define PII pair< int , int > #define v first #define w second using namespace std; const int N = 105; int n , m , l[N] , r[N] , f[N][N] , maps[N][N] , a[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void make_tree( int x )//递归建树 { for( register int i = 1 ; i <= n ; i ++ ) { if( maps[x][i] < 0 ) continue; l[x] = i , a[i] = maps[x][i]; maps[x][i] = maps[i][x] = -1; make_tree( i ); break; } for( register int i = 1 ; i <= n ; i ++ ) { if( maps[x][i] < 0 ) continue; r[x] = i , a[i] = maps[x][i]; maps[x][i] = maps[i][x] = -1; make_tree( i ); break; } return ; } inline int dfs( int i , int j ) { if( j == 0 ) return 0; if( l[i] == 0 && r[i] == 0 ) return a[i]; if( f[i][j] > 0 ) return f[i][j]; for( register int k = 0 ; k < j ; f[i][j] = max( f[i][j] , dfs( l[i] , k ) + dfs( r[i] , j - k - 1 ) + a[i] ) , k ++ ); return f[i][j]; } int main() { n = read() , m = read() + 1; memset( maps , -1 , sizeof( maps ) ); for( register int i = 1 , x , y ; i < n ; x = read() , y = read() , maps[x][y] = maps[y][x] = read() , i ++ ); make_tree( 1 ); cout << dfs( 1 , m ) << endl; return 0; } ``` ## 二次扫描与换根法给一个无根树，要求以没个节点为根统计一些信息，朴素的做法是对每个点做一次树形$DP$ 但是我们发现每次操作都会重复的统计一些信息，造成了时间的浪费，为了防止浪费我们可以用二次扫描和换根法来解决这个问题 1. 第一次扫描，任选一个点为根，在有根树上执行一次树形$DP$，在回溯时进行自底向上的转移 2. 第二次扫描，还从刚才的根节点开始，对整棵树进行一次深度优先遍历，在每次遍历前进行自顶向下的推导，计算出换根的结果 ## [AcWing 287. 积蓄程度](<https://www.acwing.com/problem/content/289/>) `g[i]`表示以$1$为根节点，`i`的子树中的最大水流，显然这个可以通过树形$DP$求出 `f[i]`表示以$i$为根节点，整颗树的最大水流，显然`f[1]=g[1]` 我们考虑如何递归的求出所以的`f[i]`，在求解这个过程是至顶向下推导的，自然对于任意点`i`，在求解之前一定知道了`f[fa]` 根据求`g[fa]`的过程我们可以知道，$fa$出了当前子树剩下的水流是`f[fa] - min( d[i] , c[i] )` 所以当前节点的最大水流就是`d[i] + min( f[fa] - min( d[i] , c[i] ) , c[i] )` 按照这个不断的转移即可，记得处理边界，也就是叶子节点的情况 ```cpp #include<bits/stdc++.h> #define PII pair< int , int > #define v first #define w second using namespace std; const int N = 2e5 + 5; int n , ans , deg[N] , f[N] , d[N]; vector<PII> e[N]; bool vis[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int y , int z ) { e[x].push_back( { y , z } ) , e[y].push_back( { x , z } ); deg[x] ++ , deg[y] ++; } inline void dp( int x ) { vis[x] = 1 , d[x] = 0; for( register auto it : e[x] ) { if( vis[it.v] ) continue; dp( it.v ); if( deg[it.v] == 1 ) d[x] += it.w; else d[x] += min( d[it.v] , it.w ); } return ; } inline void dfs( int x ) { vis[x] = 1; for( register auto it : e[x] ) { if( vis[ it.v ] ) continue; if( deg[ it.v ] == 1 ) f[ it.v ] += d[ it.v ] + it.w; else f[ it.v ] = d[ it.v ] + min( f[x] - min( d[ it.v ] , it.w ) , it.w ); dfs( it.v ); } return ; } inline void work() { for( register int i = 1 ; i <= n ; i ++ ) e[i].clear(); memset( deg , 0 , sizeof( deg ) ); n = read(); for( register int i = 1 , x , y , z ; i < n ; x = read() , y = read() , z = read() , add( x , y , z ) , i ++ ); memset( vis , 0 , sizeof( vis ) ); dp( 1 ); f[1] = d[1]; memset( vis , 0 , sizeof( vis ) ); dfs( 1 ); for( register int i = 1 ; i <= n ; i ++ ) ans = max( ans , f[i] ); printf( "%d\n" , ans ); return ; } int main() { for( register int T = read() ; T >= 1 ; work() , T -- ); return 0; } ``` # 0x55 状态压缩DP 状压 $dp$是动态规划的一种，通过将状态压缩为整数来达到优化转移的目的本小节会需要一些位运算的知识 ## [Loj #2153. 互不侵犯](<https://loj.ac/problem/2153>) 强化版？[Loj #10170.国王](<https://loj.ac/problem/10170>) `f[i][j][l]`表示第`i`行状态为`j`（用二进制表示每一位放或不放）共放了`l`个国王的方案数先用搜索预处理出每一种状态，及其所对应的国王数，在枚举状态转移即可注意要排除相互冲突的状态 ```cpp #include <bits/stdc++.h> #define LL long long using namespace std; const int N = 2005 , M = 15; LL f[M][N][N] , ans; int num[N] , s[N] , n , k , tot; inline void dfs( int x , int cnt , int cur ) { if( cur >= n ) { s[ ++ tot ] = x; num[ tot ] = cnt; return ; } dfs( x , cnt , cur + 1 );// cur 不放 dfs( x + ( 1 << cur ) , cnt + 1 , cur + 2 ); // 如果 cur 放则相邻位置不能放 return ; } inline void dp() { for( register int i = 1 ; i <= tot ; f[1][i][ num[i] ] = 1 , i ++ ); for( register int i = 2 ; i <= n ; i ++ ) // 枚举行 { for( register int j = 1 ; j <= tot ; j ++ ) // 枚举第 i 行的状态 { for( register int l = 1 ; l <= tot ; l ++ ) // 枚举 i - 1 行的状态 { if( ( s[j] & s[l] ) || ( s[j] & ( s[l] << 1 ) || ( s[j] & ( s[l] >> 1 ) ) ) ) continue;//判断冲突情况 for( register int p = num[j] ; p <= k ; p ++ ) f[i][j][p] += f[ i - 1 ][l][ p - num[j] ];//转移 } } } for( register int i = 1 ; i <= tot ; i ++ ) ans += f[n][i][k]; return ; } int main() { cin >> n >> k; dfs( 0 , 0 , 0 ); dp(); cout << ans << endl; } ``` ## [Loj #10171.牧场的安排](<https://loj.ac/problem/10171>) 与上一题不同的是不用统计数量了，状态自然就少了一维`f[i][j]`表示第`i`行状态为`j`的方案数但增加的条件就是有些点不能选择，在预处理的过程中在合法的基础上枚举状态，这样可以在后面做到很大的优化 ```cpp #include <bits/stdc++.h> using namespace std; const int N = 15 , M = 1000 , mod = 1e8 , T = 4196;//2^12 = 4096开大一点 int n , m , ans , f[N][M]; struct state { int st[T] , cnt; }a[N];//对应每行的每个状态，和每行的状态总数 inline void getstate( int x , int t ) { register int cnt = 0; for( register int i = 0 ; i < ( 1 << m ) ; i ++ ) { if( (i & ( i << 1 ) ) || ( i & ( i >> 1 ) ) || ( i & t ) ) continue;//判断冲突情况 a[x].st[ ++ cnt ] = i; } a[x].cnt = cnt; return ; } inline void init() { cin >> n >> m; for( register int i = 1 , t = 0 ; i <= n ; t = 0 , i ++ ) { for( register int j = 1 , x ; j <= m ; j ++ ) { cin >> x; t = ( t << 1 ) + 1 - x; } //是与原序列相反的 0代表可以 1代表不可以 getstate( i , t ); } return ; } inline void dp() { for( register int i = 1 ; i <= a[1].cnt ; f[1][i] = 1 , i ++ ); //预处理第一行 for( register int i = 2 ; i <= n ; i ++ )//枚举行 { for( register int j = 1 ; j <= a[i].cnt ; j ++ )//枚举第 i 行的状态 { for( register int l = 1 ; l <= a[ i - 1 ].cnt ; l ++ )//枚举第 i-1 行的状态 { if( a[i].st[j] & a[ i - 1 ].st[l] ) continue;//冲突 f[i][j] += f[ i - 1 ][l]; } } } for( register int i = 1 ; i <= a[n].cnt ; i ++ ) ans = ( ans + f[n][i] > mod ? ans + f[n][i] - mod : ans + f[n][i] );//用减法代替取模会快很多 return ; } int main() { init(); dp(); cout << ans % mod << endl; return 0; } ``` ## [Loj #10173.炮兵阵地](<https://loj.ac/problem/10173>) 这道题的状压过程和上一题很类似，所以处理的过程也很类似 `f[i][j][k]`表示第`i`行状态为`j`，第`i-1`行状态为`k`所能容纳最多的炮兵状态转移与判定合法的过程与上一题基本相同，不过本题`n`的范围比较大，会`MLE`，要用滚动数组优化 ```cpp #include<bits/stdc++.h> using namespace std; const int N = 105 , M = 12 , T = 1030; int n , m , f[3][T][T] , ans; struct state { int cnt , st[N]; }a[N]; inline bool read() { register char ch = getchar(); while( ch != 'P' && ch != 'H' ) ch = getchar(); return ch == 'H'; } inline int get_val( int t ) { register int res = 0; while( t ) { res += t & 1; t >>= 1; } return res; } inline void get_state( int x , int t ) { register int cnt = 0; for( register int i = 0 ; i < ( 1 << m ) ; i ++ ) { if( ( i & t ) || ( i & ( i << 1 ) ) || ( i & ( i << 2 ) ) || ( i & ( i >> 1 ) ) || ( i & ( i >> 2 ) ) ) continue; a[x].st[ ++ cnt ] = i; } a[x].cnt = cnt; return ; } int main() { cin >> n >> m; for( register int i = 1 , t = 0 ; i <= n ; t = 0 , i ++ ) { for( register int j = 1 , op ; j <= m ; j ++ ) { op = read(); t = ( t << 1 ) + op; } get_state( i , t ); } for( register int i = 1 ; i <= a[1].cnt ; i ++ ) { for( register int j = 1 ; j <= a[2].cnt ; j ++ ) { if( a[1].st[i] & a[2].st[j] ) continue; f[2][j][i] = get_val( a[1].st[i] ) + get_val (a[2].st[j] ); } } for( register int i = 3 ; i <= n ; i ++ ) { for( register int j = 1 ; j <= a[i].cnt ; j ++ ) { for( register int k = 1 ; k <= a[ i - 1 ].cnt ; k ++ ) { for( register int l = 1 ; l <= a[ i - 2 ].cnt ; l ++ ) { if( ( a[i].st[ j ] & a[ i - 1 ].st[ k ] ) || ( a[i].st[j] & a[ i - 2 ].st[l] ) || ( a[ i - 1 ].st[k] & a[ i - 2 ].st[l] ) ) continue; f[ i % 3 ][j][k] = max( f[ i % 3 ][j][k] , f[ ( i - 1 ) % 3 ][k][l] + get_val( a[i].st[j] ) ); } } } } for( register int i = 1 ; i <= a[n].cnt ; i ++ ) { for( register int j = 1 ; j <= a[ n - 1 ].cnt ; j ++ ) ans = max( ans , f[ n % 3 ][i][j] ); } cout << ans << endl; return 0; } ``` # 0x61 最短路 ## Dijkstra 最短路的经典做法之一，相比后面的$SPFA$，$Dij$的复杂度更低，更加的稳定但是如果出现负环时，$Dij$是不能用的 ```cpp #include <bits/stdc++.h> #define PII pair< int , int > #define F first #define S second using namespace std; const int N = 10005 , M = 500005 , INF = 0x7f7f7f7f; int n , m , s ; int dis[N]; vector< PII > e[N]; bool vis[N]; set<PII> q; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int y , int w ) { e[x].push_back( { y , w } ); } inline void dijkstra() { memset( dis , INF , sizeof( dis ) ) , dis[s] = 0; q.insert( { 0 , s } ); for( register int u ; q.size() ; ) { u = q.begin()->S , q.erase( q.begin() ); if( vis[u] ) continue; vis[u] = 1; for( register auto it : e[u] ) { if( dis[ it.F ] <= dis[u] + it.S ) continue; dis[it.F] = dis[u] + it.S; q.insert( { dis[it.F] , it.F } ); } } return ; } int main() { n = read() , m = read() , s = read(); for( register int i = 1 , x , y , z ; i <= m ; x = read() , y = read() , z = read() , add( x , y , z ) , i ++ ); dijkstra(); for( register int i = 1 ; i <= n ; printf( "%d " , ( vis[i] ? dis[i] : 0x7fffffff ) ) , i ++ ); puts(""); return 0; } ``` ### 为什么$Dijkstra$不能处理带负权边不能处理负环很简单，有负环的情况下不存在最短路，可以一直刷呢一个负环为什么不能处理负权边呢？看下面这个图 ![](https://cdn.luogu.com.cn/upload/image_hosting/w5zlojb7.png) `1`是起点，我们先把`1`加入堆中，然后开始扩展可以得到`dis[2] = 1 , dis[3] = 2` 然后取出`2`可以扩展出`dis[3] = -1` 然后取出`3`可以扩展出`dis[2] = -3`，此时就出现错误了，因为`dij`每次从堆顶取出的点一定是最短路已知的点但是如果出现负权边我们可以通过这条边扩展一条已经出队的点，与`dij`算法的前提要求冲突，所以`dij`不能处理带负权边的图 ## SPFA $SPFA$这个名字貌似只有中国人在用，国外一般叫“队列优化的`Bellman-Ford`算法” $SPFA$算法一般在判断有无负环的时候用，如果是网格图的话，不推荐使用$SPFA$，会非常的慢 ```cpp #include <bits/stdc++.h>s #define PII pair< int , int > #define F first #define S second using namespace std; const int N = 1e4+5 , M = 5e5 + 5 ; const int INF = 0x7fffffff; int n , m , s ; int dis[N]; vector< PII > e[N]; queue<int> q; bool vis[N]; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch >'9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void spfa() { for( register int i = 1 ; i <= n ; i ++ ) dis[i] = INF; q.push( s ) , vis[s] = 1 , dis[s] = 0; for( register int u ; q.size() ; ) { u = q.front() , q.pop() , vis[u] = 0; for( register auto it : e[u] ) { if( dis[u] + it.S >= dis[ it.F ] ) continue; dis[ it.F ] = dis[u] + it.S ; if( vis[it.F] ) continue; q.push( it.F ) , vis[ it.F ] = 1; } } return ; } int main() { n = read() , m = read() , s = read(); for( register int i = 1 , x , y , z ; i <= m ; x = read() , y = read() , z = read() , e[x].push_back( { y , z } ) , i ++ ); spfa(); for( register int i = 1 ; i <= n ; printf( "%d " , dis[i] ) , i ++ ); return 0; } ``` ### 判负环说道$SPFA$判断负环，常用地做法是判断每个点被松弛的次数，如果有一个点被松弛了$N$次，图中就会有负环 ### 对比Dij 其实就是看数据选择了，如果没有负权边的话，肯定是$Dijkstra$，出现负权边在考虑是否用$SPFA$ 这里在讨论一个问题，$SPFA$和$Dij$有什么本质区别，或者说原理上有什么区别 **$Dij$是按照点来扩展，$SPFA$是按照边来扩展** $Dij$按照点扩展很好理解，因为他每次都是去找距离最小的点在向外扩展，所以也很好理解为什么要用堆来维护那么$SPFA$按照边来扩展，看似没有道理吗，确实如果你单看$SPFA$你可能会觉得这玩意有什么用，很暴力的样子其实并不是，你可以先了解下$Bellman-ford$算法，枚举每一条边，扩展这边所连接的点然后根据后人的研究发现，只有经过松弛的点，所连的边才有可能会松弛其他的点，所以就有人队列优化来储存松弛过的点在说一点，$Dij$算法中堆最大是多少可以根据$Dij$是按照点连扩展的，所以一个点最多可以扩展他连接的所有的点，故堆最大就是所有点的出度之和 ## [AcWing 340. 通信线路](<https://www.acwing.com/problem/content/342/>) 二分答案，加$Dij$判断二分答案，二分第$k+1$条边的权值，小于$k+1$的边不用考虑费用，大于$k+1$的边消耗优惠活动的一个条边所以可以令大于$k+1$的边权值为$1$，其他的边权值为$0$这样跑一遍$Dij$就可以统计出有多少条边大于$k+1$条边这样就可判断其实这道题数据较水$SPFA$也可以直接过 ```cpp #include <bits/stdc++.h> #define PII pair< int , int > #define F first #define S second using namespace std; const int N = 1005 , maxline = 1e6 + 5 , INF = 0x3f3f3f3f; int n , m , k , l , r = maxline , mid , ans = -1 , dis[N]; bool vis[N]; vector< PII > e[N]; set< PII > s; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch -'0'; ch = getchar(); } return x; } inline void add( int x , int y , int z ) { e[x].push_back( { y , z } ) , e[y].push_back( { x , z } ); return ; } inline bool panding() { memset( dis , INF , sizeof( dis ) ) , memset( vis , 0 , sizeof( vis ) ) , dis[1] = 0 , s.clear() , s.insert( { 0 , 1 } ); for( register int u , cur ; s.size() ; ) { u = s.begin() -> S , s.erase( s.begin() ); if( vis[u] ) continue; vis[u] = 1; for( register auto it : e[u] ) { cur = dis[u] + ( ( it.S > mid ) ? 1 : 0 ); if( dis[it.F] <= cur ) continue; dis[it.F] = cur; s.insert( { cur , it.F } ); } } return dis[n] <= k; } int main() { n = read() , m = read() , k = read(); for( register int i = 1 , x , y , z ; i <= m ; x = read() , y = read() , z = read() , add( x , y , z ) , i ++ ); while( l <= r ) { mid = ( l + r ) >> 1; if( panding() ) ans = mid , r = mid - 1; else l = mid + 1; } cout << ans << endl; return 0; } ``` ## [Luogu P2296 寻找道路](<https://www.luogu.org/problem/P2296>) $Noip$原题，首先考虑如何满足第一个条件，反向建图，充目标点开始做$DFS$，把所有到达的点打上标记，这样如果一个点的子节点全部都被打上标记，那么这个点就满足第一条件第二个条件就是裸的最短路，直接在被标记的点的中跑一遍最短路 ```cpp #include <bits/stdc++.h> #define PII pair< int, int > #define F first #define S second using namespace std; const int N = 10005 , INF = 0x7f7f7f7f; int n , m , st , ed , dis[N]; bool vis[N] , can[N]; set< PII > s; vector<int> e[N] , t[N] ; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int y ) { e[x].push_back(y) , t[y].push_back(x); } inline void dfs( int x ) { can[x] = 1; for( register auto v : t[x] ) { if( can[v] ) continue; dfs( v ); } return ; } inline bool panding( int x ) { for( register auto v : e[x] ) { if( can[v] ) continue; return 1; } return 0; } inline void Dijkstra() { for( register int i = 1 ; i <= n ; i ++ ) dis[i] = INF; s.insert( { 0 , st } ) , dis[st] = 0; for( register int u , w; s.size() ; ) { u = s.begin() -> S , s.erase( s.begin() ); if( vis[u] ) continue; vis[u] = 1; if( panding(u) ) continue; if( u == ed ) return ; for( register auto v : e[u] ) { if( dis[v] <= dis[u] + 1 ) continue; dis[v] = dis[u] + 1; s.insert( { dis[v] , v } ); } } } int main() { n = read() , m = read(); for( register int x , y ; m >= 1 ; x = read() , y = read() , add( x , y ) , m -- ); st = read() , ed = read(); dfs(ed); Dijkstra(); cout << ( dis[ed] == INF ? -1 : dis[ed] ) << endl; return 0; } ``` ## [Loj #2590.最优贸易](<https://loj.ac/problem/2590>) `f[i]`表示`1`到`n`的路径上最大值，`g[i]`表示`i`到`n`的路径上的最小值跑两遍$Dij$，更新的时候把`f[v]= f[u] + w`变为`f[v] = max( f[u] , w )`即可最后找到`max( f[i] - g[i] )`即可 ```cpp #include<bits/stdc++.h> #define PII pair< int , int > #define F first #define S second using namespace std; const int N = 1e5 + 5 , INF = 0x7f7f7f7f; int n , m , a[N] , f[N] , g[N] , ans; bool vis[N]; vector< int > e[N] , t[N]; set< PII > s ; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } inline void add( int x , int y , int z ) { e[x].push_back(y) , t[y].push_back(x); if( !( z & 1 ) ) e[y].push_back(x) , t[x].push_back(y); return ; } inline void solove() { memset( g , INF , sizeof( g ) ) , g[1] = a[1]; s.insert( { g[1] , 1 } ); for( register int u ; s.size() ; ) { u = s.begin() -> S , s.erase( s.begin() ); if( vis[u] ) continue; vis[u] = 1; for( register auto v : e[u] ) { g[v] = min( g[u] , a[v] ); s.insert( { g[v] , v } ); } } memset( vis , 0 , sizeof( vis ) ) , memset( f , -INF , sizeof( f ) ) , f[n] = a[n]; s.insert( { f[n] , n } ); for( register int u ; s.size() ; ) { u = s.begin() -> S , s.erase( s.begin() ); if( vis[u] ) continue; vis[u] = 1; for( register auto v : t[u] ) { f[v] = max( f[u] , a[v] ); s.insert( { f[v] , v } ); } } return ; } int main() { n = read() , m = read(); for( register int i = 1 ; i <= n ; a[i] = read() , i ++ ); for( register int i = 1 , x , y , z ; i <= m ; x = read() , y = read() , z = read() , add( x , y , z ) , i ++ ); solove(); for( register int i = 1 ; i <= n ; i ++ ) ans = max( ans , f[i] - g[i] ); cout << ans << endl; return 0; } ``` ## [AcWing 342. 道路与航线 ](<https://www.acwing.com/problem/content/344/>) 因为有负权边，不能直接用$Dij$，考虑$SPFA$会$T$ 观察题面的性质，只有单向变会出现负值，先不考虑单向变会发现图变成了不连通了，但是每个连通块内没有负值了，块内可以直接跑$Dij$求最短路然后我们根据拓扑序逐个跑每个联通块内的最短路，因为拓扑序的性质，可以避免重复的松弛，来保证$Dij$的性质 ```cpp #include<bits/stdc++.h> #define pb( x ) push_back( x ) #define PII pair< int , int > #define F first #define S second using namespace std; const int N = 50005 , INF = 0x7f7f7f7f;; int n , r , p , st , tot , bl[N] , deg[N] , dis[N]; bool vis[N]; queue< int >q ; vector< int > group[N]; vector< PII > e[N]; set< PII >heap; inline int read() { register int x = 0 , f = 1; register char ch = getchar(); for( ; ch < '0' || ch > '9' ; ( ch == '-' ? f = - 1 : f ) , ch = getchar() ); for( ; ch >= '0' && ch <= '9' ; x = ( x << 3 ) + ( x << 1 ) + ch - '0' , ch = getchar() ); return x * f; } inline void add( int x , int y , int z , bool f ) { e[x].push_back( { y , z } ); if( f ) e[y].push_back( { x , z } ); return ; } inline void dfs( int x , int id ) { bl[x] = id; group[id].pb( x ); for( auto it : e[x] ) { if( bl[it.F] ) continue; dfs( it.F , id ); } return ; } inline void Dijkstra() { for( register int u ; heap.size() ; ) { u = heap.begin() -> S , heap.erase( heap.begin() ); if( vis[u] ) continue; vis[u] = 1; for( register auto it : e[u] ) { if( dis[it.F] > dis[u] + it.S ) { dis[it.F] = dis[u] + it.S; if( bl[it.F] == bl[u] ) heap.insert( { dis[it.F] , it.F } ); } if( bl[it.F] != bl[u] ) { deg[ bl[it.F] ] --; if( !deg[ bl[it.F] ] ) q.push( bl[it.F] ); } } } return ; } int main() { n = read() , r = read() , p = read() , st = read(); for( register int x , y , z ; r >= 1 ; x = read() , y = read() , z = read() , add( x , y , z , 1 ) , r -- ); for( register int i = 1 ; i <= n ; i ++ ) { if( bl[i] ) continue; dfs( i , ++ tot ); } for( register int x , y , z ; p >= 1 ; x = read() , y = read() , z = read() , add( x , y , z , 0 ) , deg[ bl[y] ] ++ , p -- ); q.push( bl[st] ); for( register int i = 1 ; i <= tot ; i ++ ) { if( deg[i] ) continue; q.push(i); } for( register int i = 1 ; i <= n ; dis[i] = INF , i ++ ); dis[st] = 0; for( register int t ; q.size() ; ) { t = q.front() , q.pop(); for( auto i : group[t] ) heap.insert( { dis[i] , i } ); Dijkstra(); } for( register int i = 1 ; i <= n ; ( dis[i] >= INF ? puts("NO PATH") : printf( "%d\n" , dis[i] ) ) , i ++ ); return 0; } ``` ## Floyd 上面给的两种算法，都只是但源多汇最短路，如果要求多源多汇最短路当然可以用`n`次$Dij$或$SPFA$来做但这样的效果并不好，这时就可以采用$Floyd$算法 ```cpp for( int i = 1 ; i <= n ; i ++ ) { for( int j = 1 ; j <= n ; j ++ ) { for( int k = 1 ; k <= n ; k ++ ) { dis[i][j] = min( dis[i][j] , dis[i][k] + dis[k][j] ); } } } ``` ## [Luogu P2910 Clear And Present Danger](luogu.org/problem/P2910) 因为这题给定的了访问点的顺序，所以我们不许要考虑顺序的问题跑一边最短路，统计下给定路径的权值和即可 ```cpp #include<bits/stdc++.h> using namespace std; const int N = 105 , M = 10005; int n , m , a[M] , dis[N][N] , sum; inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read() , m = read(); for( register int i = 1 ; i <= m ; a[i] = read() , i ++ ); a[0] = 1; for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = 1 ; j <= n ; dis[i][j] = read() , j ++ ); } for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = 1 ; j <= n ; j ++ ) { if( i == j ) continue; for( register int k = 1 ; k <= n ; k ++ ) { if( k == i || k == j ) continue; dis[i][j] = min( dis[i][j] , dis[i][k] + dis[k][j] ); } } } for( register int i = 1 ; i <= m ; sum += dis[ a[ i - 1 ] ][ a[i] ] , i ++ ); cout << sum << endl; return 0; } ``` ## [Loj #10072.Sightseeing Trip](<https://loj.ac/problem/10072>) 求最小环的经典问题，一边做$Floyd$，一边求`min( d[i][j] + d[j][k] + d[k][i] )` 但是为了方便我们统计我们保证`k`和`i`、`k`和`j`之间一定有一条边直接连接，这样就变成了`min( d[i][j] + a[j][k] + a[k][i] )`，其中`a[i][j]`表示的是原图统计路径只需要递归的去做即可 ```cpp #include <bits/stdc++.h> #define LL long long using namespace std; const int N = 310 , INF = 0x3f3f3f3f; int a[N][N] , d[N][N] , pos[N][N] , n , m , ans = INF + 1 ; vector< int > path; inline void get_path( int x , int y ) { if( pos[x][y] == 0 ) return ; get_path( x , pos[x][y] ); path.push_back( pos[x][y] ); get_path( pos[x][y] , y ); } inline int read() { register int x = 0; register char ch = getchar(); while( ch < '0' || ch > '9' ) ch = getchar(); while( ch >= '0' && ch <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ch - '0'; ch = getchar(); } return x; } int main() { n = read() , m = read(); memset( a , 0x3f , sizeof( a ) ); for( register int i = 1 ; i <= n ; i ++ ) a[i][i] = 0; for( register int i = 1 , x , y , z ; i <= m ; i ++ ) { x = read() , y = read() , z = read(); a[x][y] = a[y][x] = min( a[x][y] , z ); } memcpy( d , a , sizeof( d ) ); for( register int k = 1 ; k <= n ; k ++ ) { for( register int i = 1 ; i < k ; i ++ ) { for( register int j = i + 1 ; j < k ; j ++ ) { if( (LL)d[i][j] + a[j][k] + a[k][i] >= ans ) continue; ans = d[i][j] + a[j][k] + a[k][i]; path.clear(); path.push_back(i); get_path( i , j ); path.push_back(j); path.push_back(k); } } for( register int i = 1 ; i <= n ; i ++ ) { for( register int j = 1 ; j <= n ; j ++ ) { if( d[i][j] <= d[i][k] + d[k][j] ) continue; d[i][j] = d[i][k] + d[k][j]; pos[i][j] = k; } } } if( ans == 0x3f3f3f3f + 1 ) { puts("No solution."); return 0; } for( register int i = 0 ; i < path.size() ; i ++ ) printf("%d " , path[i] ); puts(""); return 0; } ``` # 0x62 最小生成树 ## Kruskal 起初每个点的都是一个独立的集合，把边权从小到达排序，按照边权枚举边，用并查集判断两个是否在同一个集合，如果在一个集合就跳过当前边，反之就联通这两个集合下面是[Luogu P3366](<https://www.luogu.org/problem/P3366>)的代码 ```cpp #include <bits/stdc++.h> #define PIII pair< int , pair< int , int > > #define S second #define F first using namespace std; const int N = 5005; int n , m , fa[N] , cnt , sum ; vector< PIII > e; inline int read() { register int x = 0; register char ch = getchar(); for( ; ch < '0' || ch > '9' ; ch = getchar() ); for( ; ch >= '0' && ch <= '9' ; x = ( x << 3 ) + ( x << 1 ) + ch - '0' , ch = getchar() ); return x; } inline int getfa( int x ) { if( fa[x] == x ) return x; return fa[x] = getfa( fa[x] ); } inline void Kruskal() { for( register int i = 1 ; i <= n ; fa[i] = i , i ++ ); sort( e.begin() , e.end() ); register int fx , fy ; for( auto it : e ) { fx = getfa( it.S.F ) , fy = getfa( it.S.S ); if( fx == fy ) continue; fa[fx] = fy , cnt ++ , sum += it.F; if( cnt == n - 1 ) return ; } return ; } int main() { n = read() , m = read(); for( register int i = 1 , x , y , z ; i <= m ; x = read() , y = read() , z = read() , e.push_back( { z , { x , y } } ) , i ++ ); Kruskal(); ( cnt == n - 1 ? printf( "%d\n" , sum ) : puts( "orz" ) ); return 0; } ``` ## [Luogu P2212 浇地Watering the Fields](<https://www.luogu.org/problem/P2212>) 首先读入所有的点，$O(n^2)$枚举所有的点，在枚举点的过程中直接判断掉小于$C$的点然后跑一遍$Kruskal$即可 ```cpp #include <bits/stdc++.h> #define PII pair< int , int > #define edge pair< int , PII > #define F first #define S second using namespace std; const int N = 2005; int n , c , fa[N] , sum , cnt; vector< edge > e; PII node[N]; inline int read() { register int x = 0; register char ch = getchar(); for( ; ch < '0' || ch > '9' ; ch = getchar() ); for( ; ch >= '0' && ch <= '9' ; x = ( x << 3 ) + ( x << 1 ) + ch - '0' , ch = getchar() ); return x; } inline int getlen( int x , int y ) { return ( node[x].F - node[y].F ) * ( node[x].F - node[y].F ) + ( node[x].S - node[y].S ) * ( node[x].S - node[y].S );} inline int getfa( int x ) { if( fa[x] == x ) return x; return fa[x] = getfa( fa[x] ); } inline void Kruskal() { for( register int i = 1 ; i <= n ; fa[i] = i , i ++ ); sort( e.begin() , e.end() ); register int fx , fy; for(auto it : e ) { fx = getfa( it.S.F ) , fy = getfa( it.S.S ); if( fx == fy ) continue; fa[fx] = fy , sum += it.F , cnt ++; if( cnt == n - 1 ) return ; } return ; } int main() { n = read() , c = read(); for( register int i = 1 ; i <= n ; node[i].F = read() , node[i].S = read() , i ++ ); for( register int i = 1 , d ; i <= n ; i ++) { for( register int j = i + 1 ; j <= n ; j ++ ) { d = getlen( i , j ); if( d < c ) continue; e.push_back( { d , { i , j } } ); } } Kruskal(); cout << ( cnt == n - 1 ? sum : -1 ) << endl; return 0; } ``` ## [AcWing 346. 走廊泼水节](<https://www.acwing.com/problem/content/348/>) 这道题用了$Kruskal$的思想和带权并查集首先我们把说有的边权进行排序，然后从小到大排序对于一条边$(x,y,z)$ 首先这条边要在完全图的最小生成树上，其次对于点$x,y$所在的连通块中每个点都要直接有边相连 $s(i)$表示节点$i$所在连通块点的个数，所以对于一条边$(x,y,z)$的贡献就是$[ s(x)\times s(y) + 1 ] \times ( z + 1 )$ 所以用带权并差集维护一下即可 ```cpp #include <bits/stdc++.h> #define LL long long #define PIII pair< int , pair< int , int > > #define S second #define F first using namespace std; const int N = 6005; int n , fa[N] , s[N] , fx , fy; LL ans; PIII e[N]; inline int read() { register int x = 0; register char ch = getchar(); for( ; ch < '0' || ch > '9' ; ch = getchar() ); for( ; ch >= '0' && ch <= '9' ; x = ( x << 3 ) + ( x << 1) + ch - '0' , ch = getchar() ); return x; } inline int getfa( int x ) { if( x == fa[x] ) return x; return fa[x] = getfa( fa[x] ); } inline void work() { n = read(); for( register int i = 1 , x , y ,z ; i < n ; x = read() , y = read() , z = read() , e[i] = { z , { x , y } } , i ++ ); sort( e + 1 , e + n ); ans = 0; for( register int i = 1 ; i <= n ; fa[i] = i , s[i] = 1 , i ++ ); for( register int i = 1 ; i < n ; i ++ ) { fx = getfa( e[i].S.F ) , fy = getfa( e[i].S.S ); ans += (LL)( s[fx] * s[fy] - 1 ) * ( e[i].F + 1 ); fa[fx] = fy; s[fy] += s[fx]; } printf( "%d\n" , ans ); return ; } int main() { for( register int T = read() ; T >= 1 ; work() , T -- ); } ``` # 0x63 树的直径与最近公共祖先 ## 树的直径树上两点的距离定义为，从树上一点到另一点所经过的权值当树上两点距离最大时，就称作树的直径，树的直径既可以指这个权值，也可以指这个路径 ### 两遍DFS求树的直径我们可以先从任意一点开始$DFS$，记录下当前点所能到达的最远距离，这个点为$P$ 在从$P$开始$DFS$记录下所能达到的最远点的距离，这个点为$Q$ $P,Q$就是直径的端点，$dis(P,Q)$就是直径 ```cpp void dfs( int x ) { if( dis[x] > ans ) ans = dis[x] , p = x; vis[x] = 1; for( int i = head[x] ; i ; i = e[i].next ) { if( e[i].v ) continue; dis[ e[i].v ] + e[i].w; dfs( e[i].v ); } return ; } void dfs2( int x ) { if( dis[x] > ans ) ans = dis[x] , q = x; vis[x] = 1; for( int i = head[x] ; i ; i = e[i].next ) { if( e[i].v ) continue; dis[ e[i].v ] + e[i].w; dfs( e[i].v ); } return ; } void solove() { dfs(1); ans = dis[p] = 0; memset( vis , 0 , sizeof( dis ) ); dfs2(p); cout << ans << endl } ``` 两遍$DFS$基本相同，其实两遍$BFS$也可以做到同样的效果，这里就不在赘述 ### 树形DP求树的直径设`d[x]`表示`x`所能到达的最远距离，`y`是`x`的儿子显然`d[x] = max( d[y] + w( x , y ) )` 那么`x`所在点的最长链自然就是`x`所到的最长距离加次长距离，在转移的过程中记录最大值即可 ```cpp void dp( int x ) { v[x] = 1; for( int i = head[x] ; i ; i = e[i].next ) { if( v[ e[i].v ] ) continue; dp( e[i].v ); ans = max( ans , d[x] + d[y] + e[i].w ); d[x] = max( d[x] , d[y] + e[i].w ); } return ; } ``` ## [Luogu P3629 巡逻](<https://www.luogu.org/problem/P3629>) 在不建立道路时，我们需要把每条边都经过一遍，那么我们要走的路程显然是边数二倍，即$2\times ( n - 1)$。只修建一条道路时，这条路应建在直径的两个端点处，那么我们要走的路径长度即为$2\times(n−1)−L$，其中$L$表示树的直径修建第二条道路时，又会形成一个环，那么如果两条新道路所成的环不重叠，则答案继续减小，若重叠，则两个环重叠部分需经历两次，那么我们得到如下算法： 1. 求树的直径$L_1$，将$L_1$上的边权赋值为$-1$ 2. 再求树的直径$L_2$,答案即为$2\times n-L_1-L_2$ ```cpp #include <bits/stdc++.h> using namespace std; const int SIZE = 2e5 + 100; template<typename _T> inline void read(_T &s) { s = 0; _T w = 1, ch = getchar(); while (!isdigit(ch)) { if (ch == '-') w = -1; ch = getchar(); } while (isdigit(ch)) { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); } s *= w; } template<typename _T> inline void write(_T s) { if (s < 0) putchar('-'), s = -s; if (s > 9) write(s / 10); putchar(s % 10 + '0'); } int n, k, cnt, tot = 1, ans, st, ed; int nex[SIZE << 1], lin[SIZE], ver[SIZE << 1], dis[SIZE], edge[SIZE], fa[SIZE], f[SIZE]; bool vis[SIZE]; queue <int> q; inline void add(int from, int to, int dis) { ver[++tot] = to; nex[tot] = lin[from]; edge[tot] = dis; lin[from] = tot; } inline void init() { read(n); read(k); for (int i = 1, x, y; i < n; ++i) { read(x), read(y); add(x, y, 1), add(y, x, 1); } } int bfs(int s) { memset(vis, false, sizeof(vis)); int loc = s; fa[s] = 0; vis[s] = true; dis[s] = 0; q.push(s); while (!q.empty()) { int u = q.front(); q.pop(); for (int i = lin[u]; i; i = nex[i]) { int v = ver[i]; if (!vis[v]) { vis[v] = true; q.push(v); dis[v] = dis[u] + 1; fa[v] = u; if (dis[loc] < dis[v]) loc = v; } } } return loc; } void pre_work() { st = bfs(1); ed = bfs(st); bfs(1); memset(vis, false, sizeof(vis)); if (dis[st] < dis[ed]) swap(st, ed); vis[st] = vis[ed] = true; while (dis[st] > dis[ed]) { st = fa[st]; vis[st] = true; ++cnt; } while (st != ed) { st = fa[st]; ed = fa[ed]; vis[st] = vis[ed] = true; cnt += 2; } } void sign(int u) { for (int i = lin[u]; i; i = nex[i]) { int v = ver[i]; if (v != fa[u]) { if (vis[v] && vis[u]) { edge[i] = edge[i ^ 1] = -1; } sign(v); } } } void dp(int u) { int _max = 0; for (int i = lin[u]; i; i = nex[i]) { int v = ver[i]; if (v != fa[u]) { dp(v); ans = max(ans, _max + f[v] + edge[i]); _max = max(_max, f[v] + edge[i]); } } ans = max(ans, _max); f[u] = _max; } inline void output() { if (k == 1) { write(2 * (n - 1) - cnt + 1), putchar('\n'); exit(0); } if (cnt == n - 1) { write(n + 1), putchar('\n'); exit(0); } sign(1); dp(1); write(2 * n - cnt - ans), putchar('\n'); } int main() { init(); pre_work(); output(); return 0; } ``` \]

posted @ 2021-07-27 17:07 PHarr 阅读(158) 评论(0) 编辑收藏举报

刷新页面返回顶部

运算符	解释	例子
与`&`	对应位上两个数都为\(1\)结果为\(1\)，反之为\(0\)	`101 & 001 = 001`
或`	`	对应位上两个数有一个为\(1\)结果为\(1\)，反之为\(0\)
异或`^`	对应位上两个数不同为\(1\)，反之为\(0\)	`101 ^ 100 = 001`

生活不止眼前的苟且，还有诗和远方的田野

0x01位运算

与、或、异或

取反

左移、右移

位运算的应用

代替乘除

集合运算

优化常数

0x11 栈

0x12 队列

0x13链表与邻接表

0x14 Hash

Hash 表

字符串Hash

0x15 字符串

KMP模式匹配

最小表示法

0x16 Trie

0x17 二叉堆

priority_queue

set

Huffman 树

0x21 树与图的遍历

树与图的深度优先遍历

树的DFS序

树的深度

树的重心

图的联通块划分

图的广度优先搜索遍历

拓扑排序

0x22 深度优先搜索

0x23 剪枝

0x24 迭代加深

双向搜索

0x25 广度优先搜索

0x26广搜变形

双端队列\(BFS\)

优先队列\(BFS\)

双向\(BFS\)

0x27 A*

0x28 IDA*

0x31 质数

定义

试除法

素数的筛选

Eratosthenes 筛法 （埃拉托色尼筛法）

线性筛 （欧拉筛法）

质因数分解

算数基本定理

试除法

0x32 约数

定义

算术基本定理推论

求\(N\)的正约数的集合

最大公约数

定义

定理

更相减损术

欧几里得算法

互质与欧拉函数

\(O(n)\)递推求欧拉函数

0x33同余

定义

性质

费马小定理

欧拉定理

欧拉定理推论

裴蜀定理

扩展欧几里得算法

扩展欧几里得一元线性同余方程

乘法逆元

求逆元

费马小定理

扩展欧几里得

线性递推

线性同余方程

中国剩余定理CRT

证明中国剩余定理一定有解

扩展中国剩余定理EXCRT

Eratosthenes 筛法（埃拉托色尼筛法）

线性筛（欧拉筛法）