子空间类到达角估计方法部分相关内容
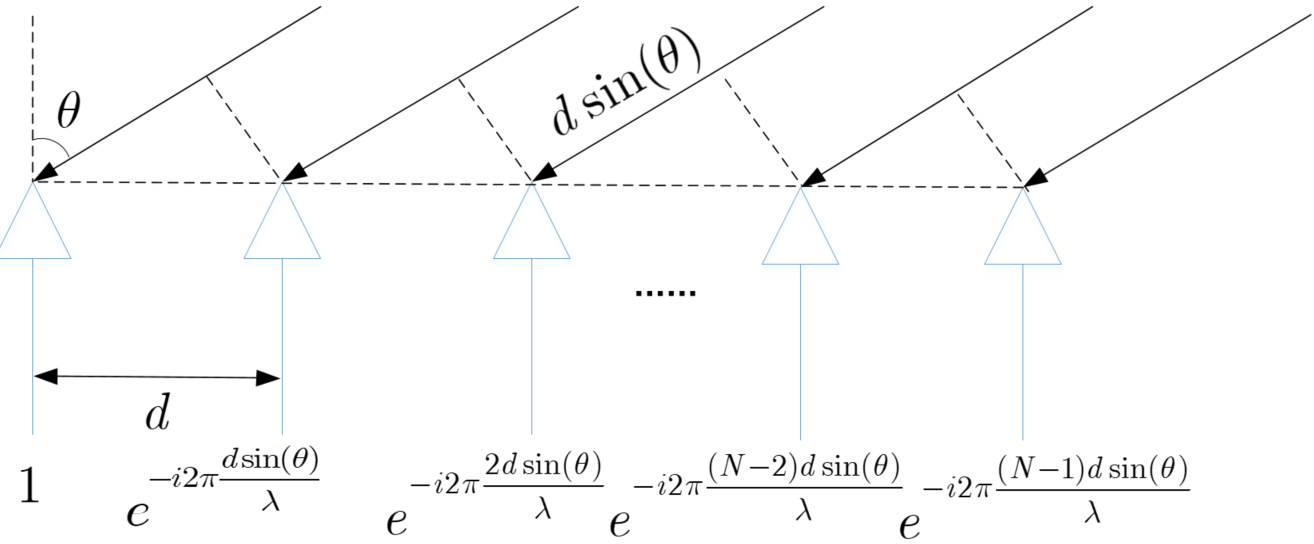
如下图所示为阵列探测示意图,其中目标到达角定义为信号入射方向与阵列法线之间的夹角,在窄带(点信源)和远场(平面波)的假设下,同一信号到达不同阵元存在波程差,这个波程差导致了各接收阵元的相位差,该相位差组成阵列的导向矢量和阵列流型矩阵,它们是到达角估计的基础和关键。
![]() 图1 阵列信号探测示意图
图1 阵列信号探测示意图
设阵元数为\(M\),信源数为\(P\),第p个信源的到达角为\(\theta_p\),则其对应的导向矢量可以表示为\(\boldsymbol{a}(\theta_p)=[1,e^{-i2\pi d{\rm sin}(\theta_p)/\lambda},...,e^{-i2\pi (M-1)d{\rm sin}(\theta_p)/\lambda}]^T\),所有信源组成的阵列流型矩阵可以表示为
\[\begin{equation}
\begin{aligned}
\boldsymbol{A}(\boldsymbol{\theta})&=[\boldsymbol{a}(\theta_0),...,\boldsymbol{a}(\theta_p),...,\boldsymbol{a}(\theta_{P-1})]\\
&=
\begin{bmatrix}
&1,&1,&...,&1\\
&e^{-i2\pi d{\rm sin}(\theta_0)/\lambda},&e^{-i2\pi d{\rm sin}(\theta_1)/\lambda},&...,&e^{-i2\pi d{\rm sin}(\theta_{P-1})/\lambda}\\
&\vdots,&\vdots,&\vdots,&\vdots\\
&e^{-i2\pi (M-1)d{\rm sin}(\theta_0)/\lambda},&e^{-i2\pi (M-1)d{\rm sin}(\theta_1)/\lambda},&...,&e^{-i2\pi (M-1)d{\rm sin}(\theta_{P-1})/\lambda}
\end{bmatrix}
\end{aligned}
\end{equation}\tag{1}
\]
从(1)可以看出,\(\boldsymbol{A}(\boldsymbol{\theta})\)是一个范德蒙矩阵,且当\(M>=P\),即信源数小于阵列维数时,阵列流型矢量是非奇异的。
所以阵列信号的接收模型可以表示为
\[\boldsymbol{x}(t)=\boldsymbol{A}(\boldsymbol{\theta})\boldsymbol{s}(t)+\boldsymbol{n}(t)\tag{2}
\]
其中\(\boldsymbol{s}(t)=[s_0(t),...,s_{P-1}(t)]^T\),\(\boldsymbol{n}(t)=[n_0(t),...,n_{P-1}(t)]^T\)。子空间类方法都是都是对协方差矩阵进行奇异值分解的操作,因此先计算接收信号的协方差矩阵
\[\begin{equation}
\begin{aligned}
\boldsymbol{R}_x&={\rm E}[\boldsymbol{x}(t)\boldsymbol{x}^H(t)]=\boldsymbol{A}{\rm E}[\boldsymbol{s}(t)\boldsymbol{s}^H(t)]\boldsymbol{A}^H+{\rm E}[\boldsymbol{n}(t)\boldsymbol{n}^H(t)]=\boldsymbol{A}\boldsymbol{R}_s \boldsymbol{A}^H+\sigma^2 \boldsymbol{I}
\end{aligned}
\end{equation}\tag{3}
\]
对协方差矩阵进行奇异值分解可以得到
\[\boldsymbol{R}_x=\boldsymbol{A}\boldsymbol{R}_s \boldsymbol{A}^H+\sigma^2 \boldsymbol{I}=\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{U}^H=[\boldsymbol{U}_s,\boldsymbol{U}_n]\begin{bmatrix}\boldsymbol{\Sigma}_s,\boldsymbol{O}\\ \boldsymbol{O},\boldsymbol{\Sigma}_n\end{bmatrix} \begin{bmatrix}\boldsymbol{U}_s^H\\\boldsymbol{U}_n^H\end{bmatrix}\tag{4}
\]
其中\(\boldsymbol{\Sigma}_s={\rm diag}(\sigma_0^2+\sigma^2,...,\sigma_{P-1}^2+\sigma^2)\),\(\boldsymbol{\Sigma}_n=\sigma^2 \boldsymbol{I}\),\(\boldsymbol{U}_s\)和\(\boldsymbol{U}_n\)分别表示信号子空间和噪声子空间对应的特征向量。进一步地,如果令\(\boldsymbol{U}=[\boldsymbol{u}_1,...,\boldsymbol{u}_P, |\boldsymbol{u}_{P+1},...,\boldsymbol{u}_M]\),则\(\boldsymbol{U}_s=[\boldsymbol{u}_1,...,\boldsymbol{u}_P]\),\(\boldsymbol{U}_n=[\boldsymbol{u}_{P+1},...,\boldsymbol{u}_M]\)。子空间定义如下:
向量组\(\lbrace \boldsymbol{a}_1,...,\boldsymbol{a}_P \rbrace\)的线性组合的集合,称为\(\lbrace \boldsymbol{a}_1,...,\boldsymbol{a}_P \rbrace\)张成的子空间,即\({\rm span} \lbrace \boldsymbol{a}_1,...,\boldsymbol{a}_P \rbrace=\lbrace \sum_{i=1}^p \beta_i \boldsymbol{a}_i \rbrace\)
则有
\[{\rm span} \lbrace \boldsymbol{s}_1,...,\boldsymbol{s}_P \rbrace={\rm span} \lbrace \boldsymbol{u}_1,...,\boldsymbol{u}_P \rbrace\\
{\rm span} \lbrace \boldsymbol{n}_1,...,\boldsymbol{n}_{M-P} \rbrace={\rm span} \lbrace \boldsymbol{u}_{P+1},...,\boldsymbol{u}_M \rbrace\\
\]
根据奇异值分解的性质可以知道,奇异值分解得到的特征矩阵\(\boldsymbol{U}\)是一个酉矩阵,所以其任意列组成的矩阵都是正交的,它本身就是一组标准正交基,所以有\(\boldsymbol{U}_s^H \boldsymbol{U}_n=0\),即信号子空间和噪声子空间是相互正交的。但是在子空间类到达角估计算法中利用的是阵列流型和噪声子空间之间的正交性,下面来证明这个正交性:
\[\begin{equation}
\begin{aligned}
\boldsymbol{R}_x \boldsymbol{U}_n&=[\boldsymbol{A}\boldsymbol{R}_s \boldsymbol{A}^H+\sigma^2 \boldsymbol{I}]\boldsymbol{U}_n=[\boldsymbol{U}_s,\boldsymbol{U}_n]\begin{bmatrix}\boldsymbol{\Sigma}_s,\boldsymbol{O}\\ \boldsymbol{O},\boldsymbol{\Sigma}_n\end{bmatrix} \begin{bmatrix}\boldsymbol{U}_s^H\\\boldsymbol{U}_n^H\end{bmatrix}\boldsymbol{U}_n=[\boldsymbol{U}_s,\boldsymbol{U}_n]\begin{bmatrix}\boldsymbol{\Sigma}_s,\boldsymbol{O}\\ \boldsymbol{O},\boldsymbol{\Sigma}_n\end{bmatrix} \begin{bmatrix}\boldsymbol{O}\\\boldsymbol{I}\end{bmatrix}\\
&=\sigma^2 \boldsymbol{U}_n
\end{aligned}
\end{equation}
\]
从上面的表达式有\(\boldsymbol{A}\boldsymbol{R}_s\boldsymbol{A}^H \boldsymbol{U}_n=\boldsymbol{0}\),显然,当信号源数小于阵列维数时,\(\boldsymbol{A}\)是满列秩的,而当信号中不存在相干信号时\(\boldsymbol{R}_s\)是可逆的,所以上面的表达式要想成立只能是\(\boldsymbol{A}^H \boldsymbol{U}_n=\boldsymbol{0}\),所以阵列流型是与噪声子空间正交的。从上面的证明过程也可以看出,当存在相干信源时,\(\boldsymbol{R}_s\)是奇异的,此时\(\boldsymbol{A}^H \boldsymbol{U}_n\neq \boldsymbol{0}\),所以信号泄露到噪声子空间中去了,此时子空间类算法应用将出问题,因此需要进行解相干。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号