恒虚警检测在数据边缘处的处理方法
如图1所示为恒虚警检测的实施示意图，其中淡蓝色方框表示参考窗，红色方框表示待检单元，黑色大方框表示检测范围，可以看出当待检单元出现在检测边缘附近的位置时，参考窗中并非都有数据。以下分析常见恒虚警检测算法(CA-CFAR、OS-CFAR、GO-CFAR、SO-CFAR)在边缘位置处的具体实施方法。
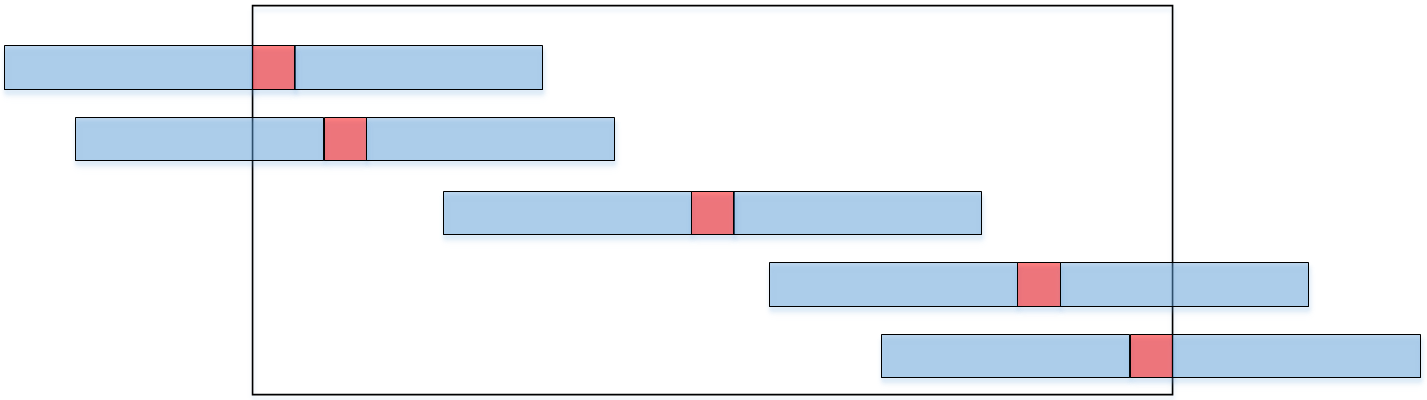图1 恒虚警检测实施过程示意图
设参考窗长为\(N\)，当待检单元不在边缘附近的位置时，此时参考窗数据是完整的，其相关理论分析和实现过程可以参考《均匀背景下常用恒虚警检测推导及比较》。当待检单元在边缘位置时，参考窗数据存在欠缺，此时需要在常规CFAR操作的基础上进行调整，以适应真实的检测情况。
(1)CA-CFAR 和 OS-CFAR
由于CA-CFAR和OS-CFAR的检测门限是对前后参考窗形成的整体进行操作得到的，因此当参考窗数据有欠缺时，它们的整个处理流程和正常条件下的处理流程是完全一样的，只需要将参考窗长度设置成与真实的参考窗数据对应即可。
(2)GO-CFAR 和 SO-CFAR
GO-CFAR和SO-CFAR需要对前后参考窗中的数据进行单独处理，当前后参考窗长度不一致时，前、后参考窗中各单元的联合概率密度函数是不一样的，因此不能按照《均匀背景下常用恒虚警检测推导及比较》推导得到的概率密度函数进行后续的计算，故需要重新进行推导。
设前参考窗数据长度为\(n_1\)，后参考窗数据长度为\(n_2\)，在平方率检波以及单元指数分布的假设条件下，前、后参考窗单元的联合概率密度函数以及分布函数可以分别表示为
\[\begin{equation}
\begin{aligned}
Z_1 \backsim G(n_1,\lambda_1):f_{z_1}(z)&=\frac{\lambda_1^{n_1}}{\Gamma(n_1)}z^{n_1-1}e^{-\lambda_1 z}\\
Z_2 \backsim G(n_2,\lambda_2):f_{z_2}(z)&=\frac{\lambda_2^{n_2}}{\Gamma(n_2)}z^{n_2-1}e^{-\lambda_2 z}\\
F_{z_1}(z)&=1-e^{-\lambda_1 z}\sum_{k=0}^{n_1-1}\frac{\lambda_1^k}{k!}z^k\\
F_{z_2}(z)&=1-e^{-\lambda_2 z}\sum_{k=0}^{n_2-1}\frac{\lambda_2^k}{k!}z^k\\
\end{aligned}
\end{equation}\tag{1}
\]
在上面的表达式中\(\lambda_1=n_1\lambda_0,\lambda_2=n_2\lambda_0\)，其中\(\lambda_0\)背景噪声对应的指数分布参数。同时需要注意的是为了保证(1)中Gamma函数是有意义的，要求\(n_1\geq 1,n_2\geq 1\)，所以以下推导结果并适用于只有单边参考窗的情况，那种情况需要单独分析。对于GO-CFAR和SO-CFAR整个参考单元的联合概率密度函数可以分别表示为
\[\begin{equation}
\begin{aligned}
{\rm GO}: &f_z(z)=f_{z_1}(z)F_{z_2}(z)+f_{z_2}(z)F_{z_1}(z)\\
&=\frac{\lambda_1^{n_1}}{\Gamma(n_1)}z^{n_1-1}e^{-\lambda_1 z}+\frac{\lambda_2^{n_2}}{\Gamma(n_2)}z^{n_2-1}e^{-\lambda_2 z}\\
&-\frac{\lambda_1^{n_1}}{\Gamma(n_1)}\sum_{k=0}^{n_2-1}\frac{\lambda_2^k}{k!}z^{n_1+k-1}e^{-(\lambda_1+\lambda_2)z}-\frac{\lambda_2^{n_2}}{\Gamma(n_2)}\sum_{k=0}^{n_1-1}\frac{\lambda_1^k}{k!}z^{n_2+k-1}e^{-(\lambda_1+\lambda_2)z}\\
{\rm SO}: &f_z(z)=f_{z_1}(z)[1-F_{z_2}(z)]+f_{z_2}(z)[1-F_{z_1}(z)]\\
&=\frac{\lambda_1^{n_1}}{\Gamma(n_1)}\sum_{k=0}^{n_2-1}\frac{\lambda_2^k}{k!}z^{n_1+k-1}e^{-(\lambda_1+\lambda_2)z}+\frac{\lambda_2^{n_2}}{\Gamma(n_2)}\sum_{k=0}^{n_1-1}\frac{\lambda_1^k}{k!}z^{n_2+k-1}e^{-(\lambda_1+\lambda_2)z}
\end{aligned}
\end{equation}\tag{2}
\]
根据矩母函数和概率密度函数的对应关系:
\[{\rm M}_z(t)=\int_0^\infty f_z(z)e^{-tz}dz\tag{3}
\]
可以求得，GO-CFAR和SO-CFAR对应的矩母函数为：
\[\begin{equation}
\begin{aligned}
{\rm GO}: {\rm M}_z(t)&=(1+t/\lambda_1)^{-n_1}+(1+t/\lambda_2)^{-n_2}+\\
&-\lambda_1^{n_1}\sum_{k=0}^{n_2-1}\lambda_2^k \begin{pmatrix}n_1+k-1\\k\end{pmatrix}(\lambda_1+\lambda_2+t)^{-(n_1+k)}\\
&-\lambda_2^{n_2}\sum_{k=0}^{n_1-1}\lambda_1^k \begin{pmatrix}n_2+k-1\\k\end{pmatrix}(\lambda_1+\lambda_2+t)^{-(n_2+k)}\\
{\rm SO}: {\rm M}_z(t)&=\lambda_1^{n_1}\sum_{k=0}^{n_2-1}\lambda_2^k \begin{pmatrix}n_1+k-1\\k\end{pmatrix}(\lambda_1+\lambda_2+t)^{-(n_1+k)}\\
&+\lambda_2^{n_2}\sum_{k=0}^{n_1-1}\lambda_1^k \begin{pmatrix}n_2+k-1\\k\end{pmatrix}(\lambda_1+\lambda_2+t)^{-(n_2+k)}
\end{aligned}
\end{equation}\tag{4}
\]
所以GO-CFAR和SO-CFAR的虚警概率和检测概率可以分别表示为
\[\begin{equation}
\begin{aligned}
{\rm GO}: P_D={\rm M}_z(\alpha \lambda_t)&=(1+\frac{\alpha}{n_1{\rm SNR}})^{-n_1}+(1+\frac{\alpha}{n_2{\rm SNR}})^{-n_2}+\\
&-n_1^{n_1}\sum_{k=0}^{n_2-1}n_2^k \begin{pmatrix}n_1+k-1\\k\end{pmatrix}(n_1+n_2+\alpha/{\rm SNR})^{-(n_1+k)}\\
&-n_2^{n_2}\sum_{k=0}^{n_1-1}n_1^k \begin{pmatrix}n_2+k-1\\k\end{pmatrix}(n_1+n_2+\alpha/{\rm SNR})^{-(n_2+k)}\\
P_{FA}={\rm M}_z(\alpha \lambda_0)&=(1+\alpha/n_1)^{-n_1}+(1+\alpha/n_2)^{-n_2}+\\
&-n_1^{n_1}\sum_{k=0}^{n_2-1}n_2^k \begin{pmatrix}n_1+k-1\\k\end{pmatrix}(n_1+n_2+\alpha)^{-(n_1+k)}\\
&-n_2^{n_2}\sum_{k=0}^{n_1-1}n_1^k \begin{pmatrix}n_2+k-1\\k\end{pmatrix}(n_1+n_2+\alpha)^{-(n_2+k)}\\
{\rm SO}: P_D={\rm M}_z(\alpha \lambda_t)&=n_1^{n_1}\sum_{k=0}^{n_2-1}n_2^k \begin{pmatrix}n_1+k-1\\k\end{pmatrix}(n_1+n_2+\alpha/{\rm SNR})^{-(n_1+k)}\\
&+n_2^{n_2}\sum_{k=0}^{n_1-1}n_1^k \begin{pmatrix}n_2+k-1\\k\end{pmatrix}(n_1+n_2+\alpha/{\rm SNR})^{-(n_2+k)}\\
P_{FA}={\rm M}_z(\alpha \lambda_0)&=n_1^{n_1}\sum_{k=0}^{n_2-1}n_2^k \begin{pmatrix}n_1+k-1\\k\end{pmatrix}(n_1+n_2+\alpha)^{-(n_1+k)}\\
&+n_2^{n_2}\sum_{k=0}^{n_1-1}n_1^k \begin{pmatrix}n_2+k-1\\k\end{pmatrix}(n_1+n_2+\alpha)^{-(n_2+k)}\\
\end{aligned}
\end{equation}\tag{4}
\]
所以现在GO-CFAR和SO-CFAR需要根据(4)(5)得到的虚警概率表达来计算门限乘积因子\(\alpha\)，其具体实现流程可以参考《均匀背景下常用恒虚警检测推导及比较》中的二分法。GO-CFAR和SO-CFAR的后续操作过程和正常情况下的操作流程是一致的。
注：
当检测点位于边缘处时，出现半参考窗情况，即此时只有前参考窗或后参考窗，因此此时GO-CFAR和OS-CFAR的已经没有成立的意义了，此时可以将两者全部按CA-CFAR进行处理。
