随机变量概率密度函数和概率分布函数相关总结
概率密度函数和概率分布函数的基本概念:
随机变量是指在任何时间点上,值都是不能完全确定的,最多只能知道它可能落在哪个区间上,那么怎样去描述这个变量呢?只能通过概率。概率密度函数(Probability Density Function, PDF)和概率分布函数(又称累积分布函数, Cumulative Distribution Function, CDF)分别从两个不同的角度来描述随机变量的概率。在说明PDF和CDF之前,首先来看一个统计问题,对于一组随机数,通常可以利用直方图来表示这组随机数在各个区间上的分布情况,如下图所示为随机生成100000个高斯分布的样本

显然\(f(x) \geq 0\),且\(\int_{x_1}^{x_2} {f(x)dx}=1\),为了从数学上更好地表示\((1)\),我们定义了CDF,其定义方式如下:
从\((1)\)可以看出\(F(x)\)暗含着概率累积的概念,这也就是它为什么又叫做累积分布函数的原因,这通过离散型随机变量的例子可以很容易理解,比如随机变量\(X\)的取值是\(0 \backsim 5\)的整数,则\(F(3)=P(X \leq 3)=P(0)+P(1)+P(2)+P(3)\)。对比\((1)(2)\)两式可得
\((3)\)给出了PDF和CDF之间的关系,除此之外,它们还有如下一些常用的性质:
- \(F(x)\)是一个不减函数,即\(F(x_2)-F(x_1)=P(x_1 < x \leq x_2) \geq 0\),其中\(x_1 < x_2\);
- \(0 \leq F(x) \leq 1\),且\(F(-\infty)=\lim_{x \to -\infty}{F(x)}=P(X < -\infty)=0\),\(F(\infty)=\lim_{x \to \infty}{F(x)}=P(X < \infty)=1\);
- \(F(x)=\int_{-\infty}^x{f(t)dt}\),\(F'(x)=f(x)\)。
显然,当知道一个随机变量的PDF或CDF之后,该随机变量就能被很好描述了,所以确定随机变量的PDF或CDF是随机变量处理中的非常重要的一个内容。
PDF和CDF的更详细的信息,可以参考相关资料,比如《概率分布函数、概率密度函数》
上面讨论的都是一个随机变量的情况,在实际情况中经常需要考虑多个随机变量,下面以二维随机变量为例进行简单的说明。设\(X\),\(Y\)为两个随机变量,显然它们各自都有对应的PDF和CDF,分别记为\(f_X(x),F_X(x)\)和\(f_Y(y),F_Y(y)\),同时这两个随机变量还共同组成一个PDF和CDF,记为\(f_{XY}(x,y),F_{XY}(x,y)\),则上面各个变量之间存在如下一些常用的基本的关系:
- \(F_{XY}(x,y)=P(X \leq x,Y \leq y)=\int_{-\infty}^y{\int_{-\infty}^x{f(\mu,\upsilon)d\mu d\upsilon}}\),\(F_{XY}(-\infty,\infty)=\int_{-\infty}^{\infty}{\int_{-\infty}^{\infty}{f(x,y)dx dy}}=1\);
- \(f_{XY}(x,y)=\frac{\partial^2 F_{XY}(x,y)}{\partial x \partial y}\)
- \(F_X(x)=F_{XY}(x,\infty),F_Y(y)=F_{XY}(\infty,y),f_X(x)=\int_{-\infty}^{\infty}{f_{XY}(x,y)dy},f_Y(y)=\int_{-\infty}^{\infty}{f_{XY}(x,y)dx}\)
需要注意的是各随机变量之间可能是相关的,也就是彼此可能相互影响,所以综合的PDF和CDF不仅与每个随机变量各自的PDF和CDF有关,还和它们彼此之间的相关性有关。考虑一种最简单的情况,即当所有随机变量互相独立时,此时可以得到以下常用的结论:
- \(P(X \leq x,Y \leq y)=P(X \leq x)P(Y \leq y),F_{XY}(x,y)=F_X(x)F_Y(y),f_{XY}(x,y)=f_X(x)f_Y(y)\)
更多多维随机变量相关内容可以查阅资料,如《多维随机变量》
随机变量函数的概率密度函数和概率分布函数:
在实际应用中往往关注的不是某个随机变量的分布特征,而是这个随机变量某个函数的分布特征,比如在对复随机信号进行处理时,我们往往并不会关注它的实部、虚部分别满足什么样的分布,而是更希望了解它的幅度或功率的分布情况。因此需要探究如何根据已知随机变量的分布情况,求它的某个函数的分布情况,首先来考虑单个随机变量的情况,设随机变量\(X\)的PDF和CDF分别为\(f_X(x),F_X(x)\),\(Y=g(X)\)为随机变量\(X\)的一个函数,现在需要求解\(Y\)的分布规律。求解方法如下:
上面的式子仅展示了一个基本的求解思路,并不严谨,基本的思路就是利用函数表达式\(Y=g(X)\),将\(X\)表示为\(Y\)的函数,即\(X=h(Y)\),这样就能利用\(X\)的分布情况来求\(Y\)的分布情况,以下给出更严谨的定理:
设随机变量\(X\)具有PDF\(f_X(x),-\infty < x < \infty\),又设函数\(g(x)\)处处可导且恒有\(g'(x)>0\)(或恒有\(g'(x)< 0\)),则\(Y=g(X)\)是连续型随机变量,其概率密度函数为
其中\(\alpha=min[g(-\infty),g(\infty)],\beta=max[g(-\infty),g(\infty)]\),\(h(y)\)是\(g(x)\)的反函数。
上面给出了单个随机变量的函数的PDF求解方法,对于多个随机变量函数的PDF,可以按照类似的思路进行处理,但是因为涉及到多个变量,显然求解的过程会复杂很多,一般也没有一个通用的表达式,通常也只需要根据实际情况进行具体的求解,以下通过两个随机变量函数的PDF求解来展示一下基本的过程:
(1) \(Z=X+Y\)的分布
所以\(f_Z(z)=\int_{-\infty}^{\infty}{f_{XY}(z-y,y)dy}\),由于\(x,y\)在上面的式子中是完全对称的,所以显然有\(f_Z(z)=\int_{-\infty}^{\infty}{f_{XY}(x,z-x)dx}\),当\(X,Y\)相互独立时,\(f_{XY}(x,y)=f_X(x)f_Y(y)\),所以此时\(f_Z(z)=\int_{-\infty}^{\infty}{f_X(z-y)f_Y(y)dy}\)或\(f_Z(z)=\int_{-\infty}^{\infty}{f_X(x)f_Y(z-x)dx}\),可以看出此时随机变量\(Z\)的PDF是随机变量\(X,Y\)的PDF的卷积。
由于两个高斯函数的卷积仍然为高斯函数,因此根据上面的结论可得,两个服从高斯分布的相互独立的随机变量的和仍然服从高斯分布,更具体地:
设\(X\),\(Y\)相互独立且\(X \backsim N(\mu_x,\sigma_x^2)\),\(Y \backsim N(\mu_y,\sigma_y^2)\),则\(Z=X+Y\)仍然服从高斯分布,且\(Z \backsim N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2)\)。进一步地,有限个相互独立的正态随机变量的线性组合仍然服从正态分布,且若\(X_i \backsim N(\mu_i,\sigma_i^2),i=1,2,...,n\),\(Z=\sum_{i=1}^n{k_i X_i}\),则\(Z \backsim N(\sum_{i=1}^n{k_i \mu_i},\sum_{i=1}^n{k_i^2 \sigma_i^2})\)
(2) \(Z=Y/X\)的分布
所以\(f_Z(z)=\int_{-\infty}^{\infty}{|x|f_{XY}(x,xz)dx}\),当\(X,Y\)相互独立时,\(f_{XY}(x,y)=f_X(x)f_Y(y)\),所以此时\(f_Z(z)=\int_{-\infty}^{\infty}{|x|f_X(x)f_Y(xz)dx}\)。
(3) \(Z=XY\)的分布
所以\(f_Z(z)=\int_{-\infty}^{\infty}{\frac{1}{|x|}f_{XY}(x,z/x)dx}\),当\(X,Y\)相互独立时,\(f_{XY}(x,y)=f_X(x)f_Y(y)\),所以此时\(f_Z(z)=\int_{-\infty}^{\infty}{\frac{1}{|x|}f_X(x)f_Y(z/x)dx}\)。
除了上述常见的随机变量函数的分布以外,复随机信号的分布也是在实际问题中经常会遇到的内容,以下来推导几个与复随机信号相关的常见的分布。
1.设\(X \backsim N(\mu_x,\sigma_x^2)\),\(Y \backsim N(\mu_y,\sigma_y^2)\),且两者相互独立,\(Z=X+iY\),显然根据上面1)的结论可知,\(Z\)也服从高斯分布,此时\(Z\)的PDF可以参考《正态分布》
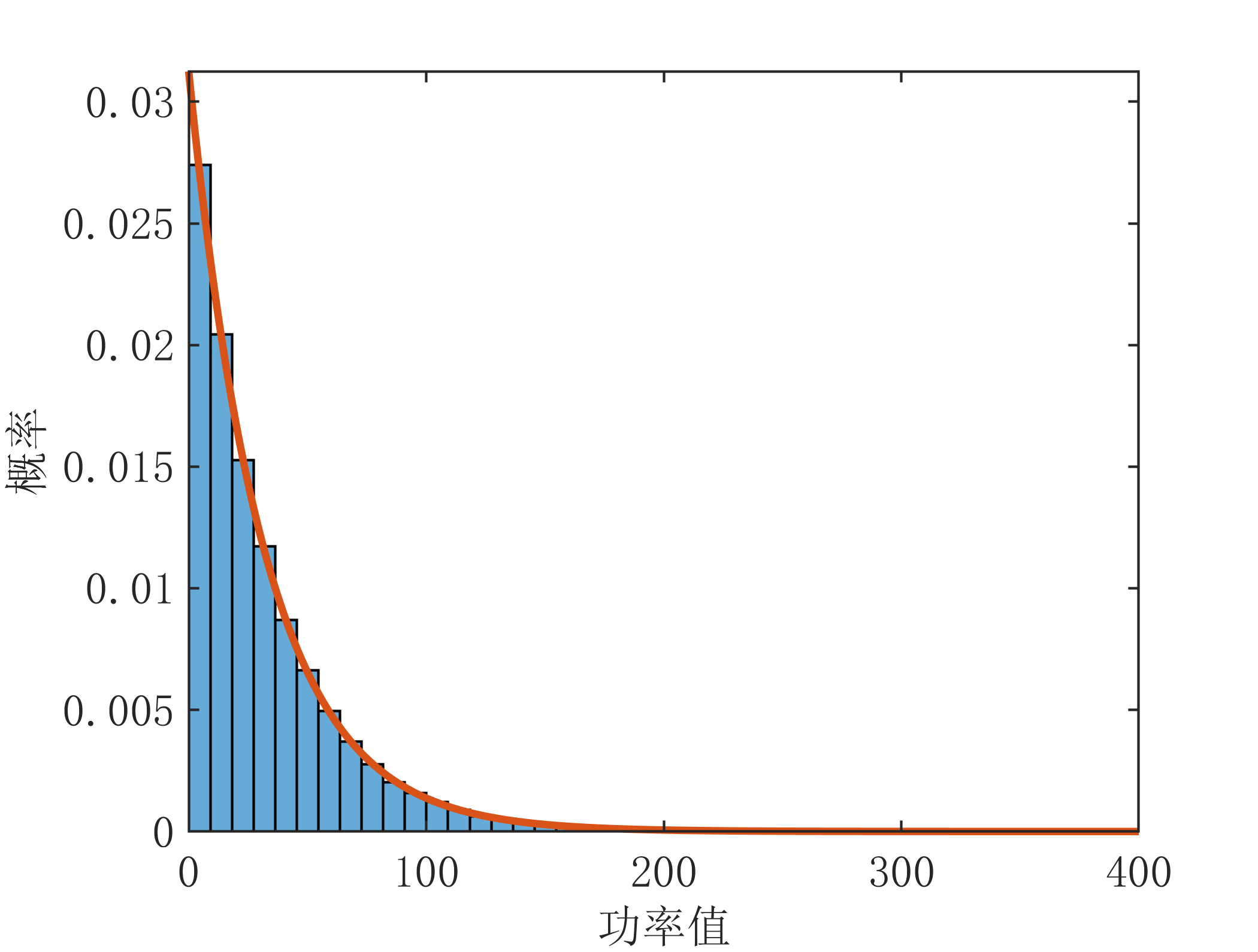
2.设\(X \backsim N(0,\sigma^2)\),\(Y \backsim N(0,\sigma^2)\),且两者相互独立,则\(Z=X^2+Y^2\)服从指数分布,其PDF可通过下面的方法进行求解:
所以 \(f_Z(z)=F_Z^{'}(z)=\frac{1}{2\sigma^2}{\rm exp}(-\frac{z}{2\sigma^2})\)。
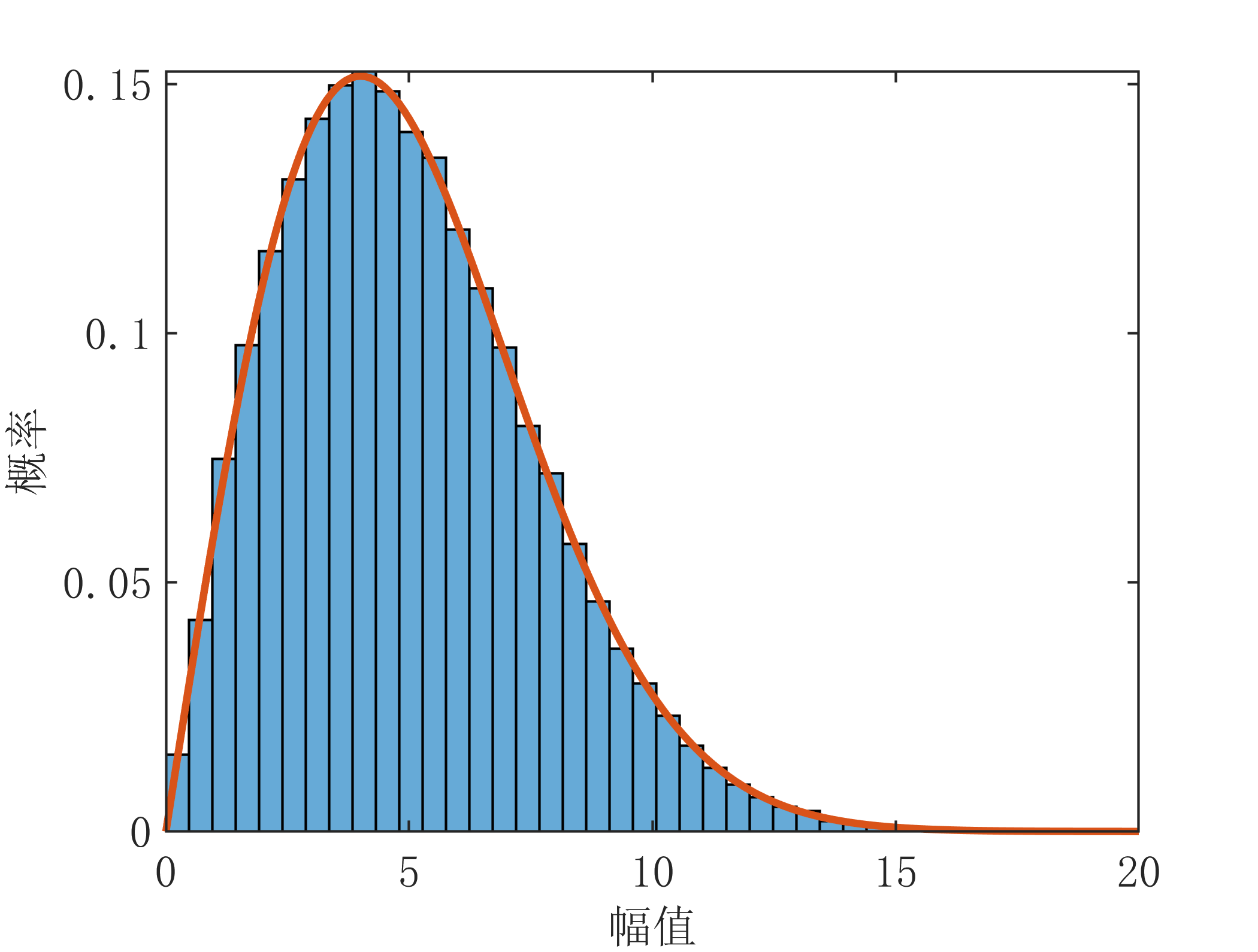
3.设\(X \backsim N(0,\sigma^2)\),\(Y \backsim N(0,\sigma^2)\),且两者相互独立,则\(Z=\sqrt{X^2+Y^2}\)服从瑞利分布,其PDF可通过下面的方法进行求解:
所以 \(f_Z(z)=F_Z^{'}(z)=\frac{z}{\sigma^2}{\rm exp}(-\frac{z^2}{2\sigma^2})\)
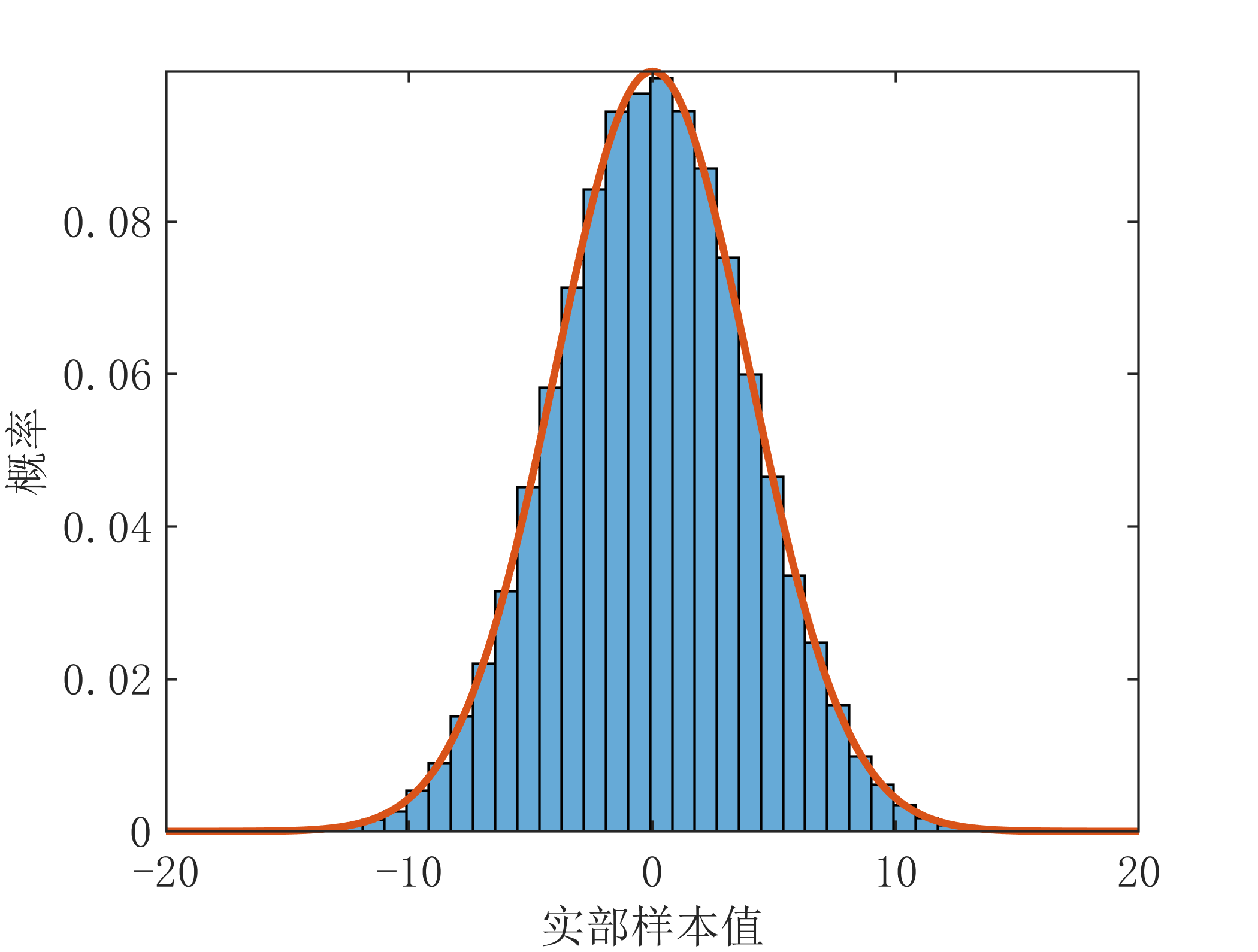
下面对上述复高斯变量的幅度和功率的分布进行仿真验证,仿真代码如下:
mu=0;sigma=4; %高斯分布的均值和方差
x=sigma*randn(100000,1)+mu; %实部的值
y=4*randn(100000,1)+mu; %虚部的值
z1=sqrt(x.^2+y.^2); %模值
z2=x.^2+y.^2; %功率值
s=-20:0.1:20;
x_=exp(-(s-mu).^2./(2*sigma^2))./(sigma*sqrt(2*pi));%理论高斯分布概率密度函数
y_=exp(-(s-mu).^2./(2*sigma^2))./(sigma*sqrt(2*pi));%理论高斯分布概率密度函数
s1=0:0.1:20;
z1_=s1/sigma^2.*exp(-s1.^2/(2*sigma^2)); %理论瑞利分布概率密度函数
s2=0:0.1:400;
z2_=1/(2*sigma^2).*exp(-s2/(2*sigma^2)); %理论指数分布概率密度函数
histogram(x,'Normalization','pdf','NumBins',40);
hold on;
plot(s,x_,'LineWidth',1.5);xlabel('实部样本值');ylabel('概率');axis tight;
figure;
histogram(y,'Normalization','pdf','NumBins',40);
hold on;
plot(s,y_,'LineWidth',1.5);xlabel('实部样本值');ylabel('概率');axis tight;
figure;
histogram(z1,'Normalization','pdf','NumBins',40);
hold on;
plot(s1,z1_,'LineWidth',1.5);xlabel('幅值');ylabel('概率');axis tight;
figure;
histogram(z2,'Normalization','pdf','NumBins',40);
hold on;
plot(s2,z2_,'LineWidth',1.5);xlabel('功率值');ylabel('概率');axis tight;
运行结果如下:

随机样本\(X\)的常用统计分布:
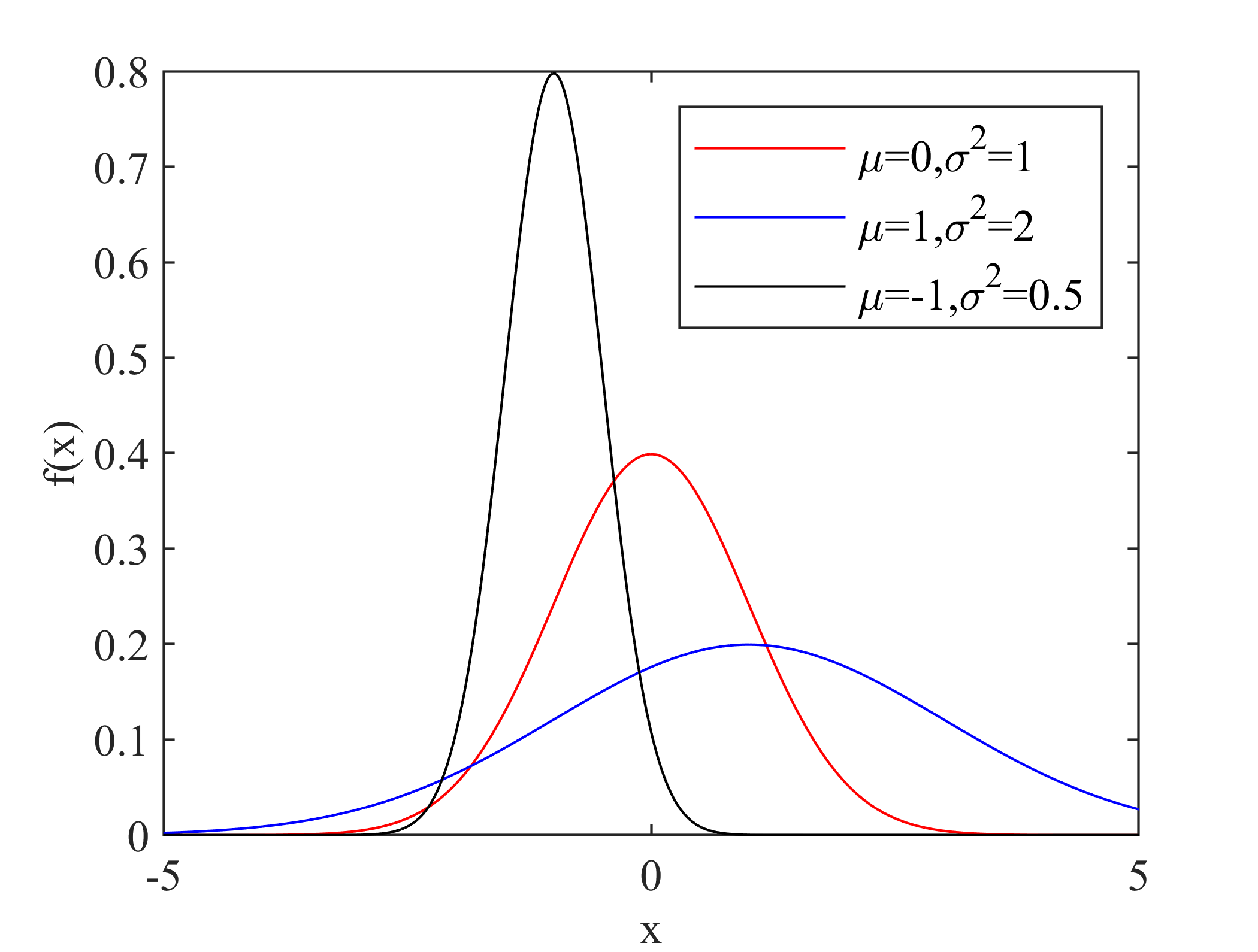
(1)正态分布
其概率密度函数可以表示为:
其中\(\mu\),\(\sigma^2\)分别表示均值和方差,当\(\mu=0\),\(\sigma^2=1\)时,服从标准正态分布,其概率密度函数可以表示为:
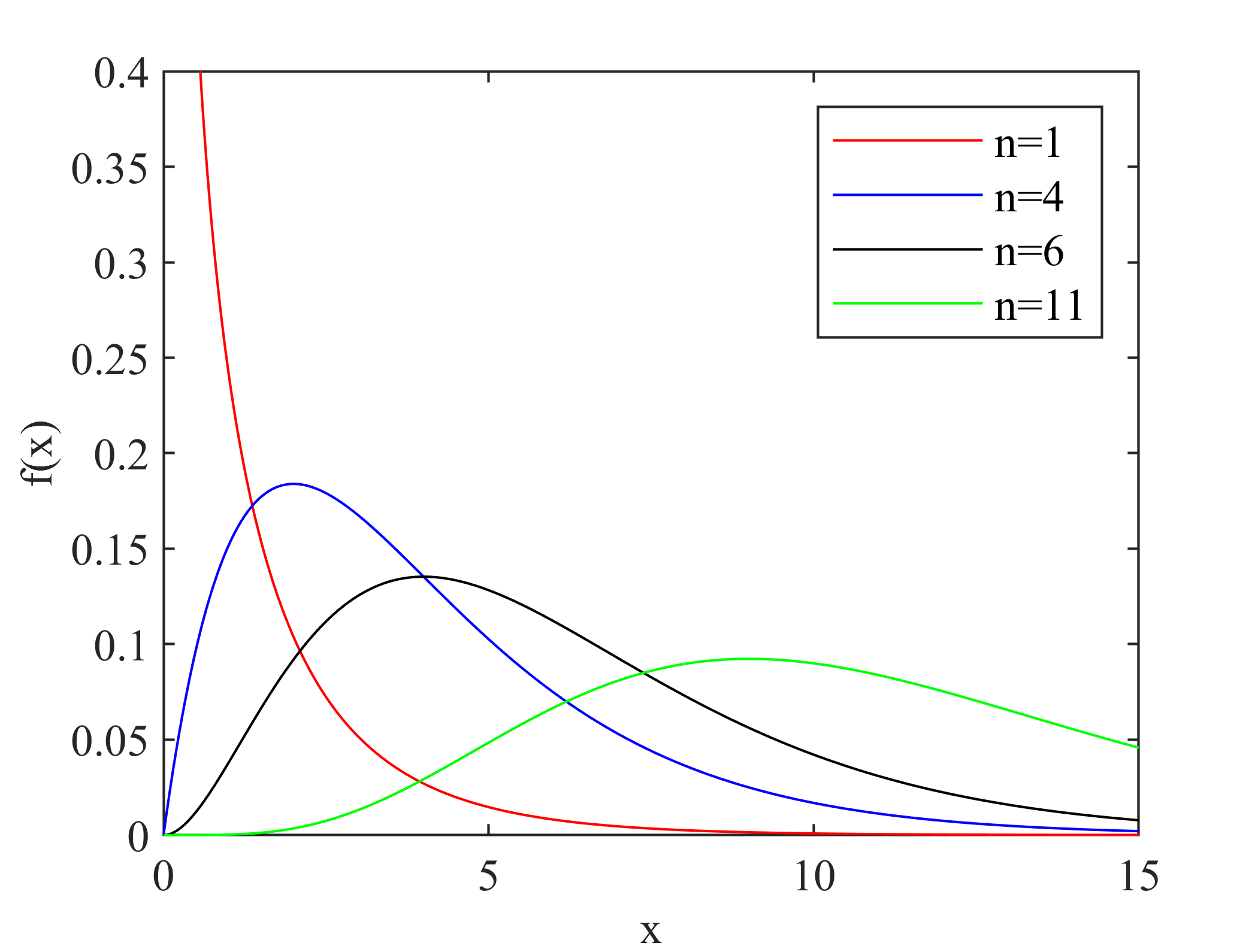
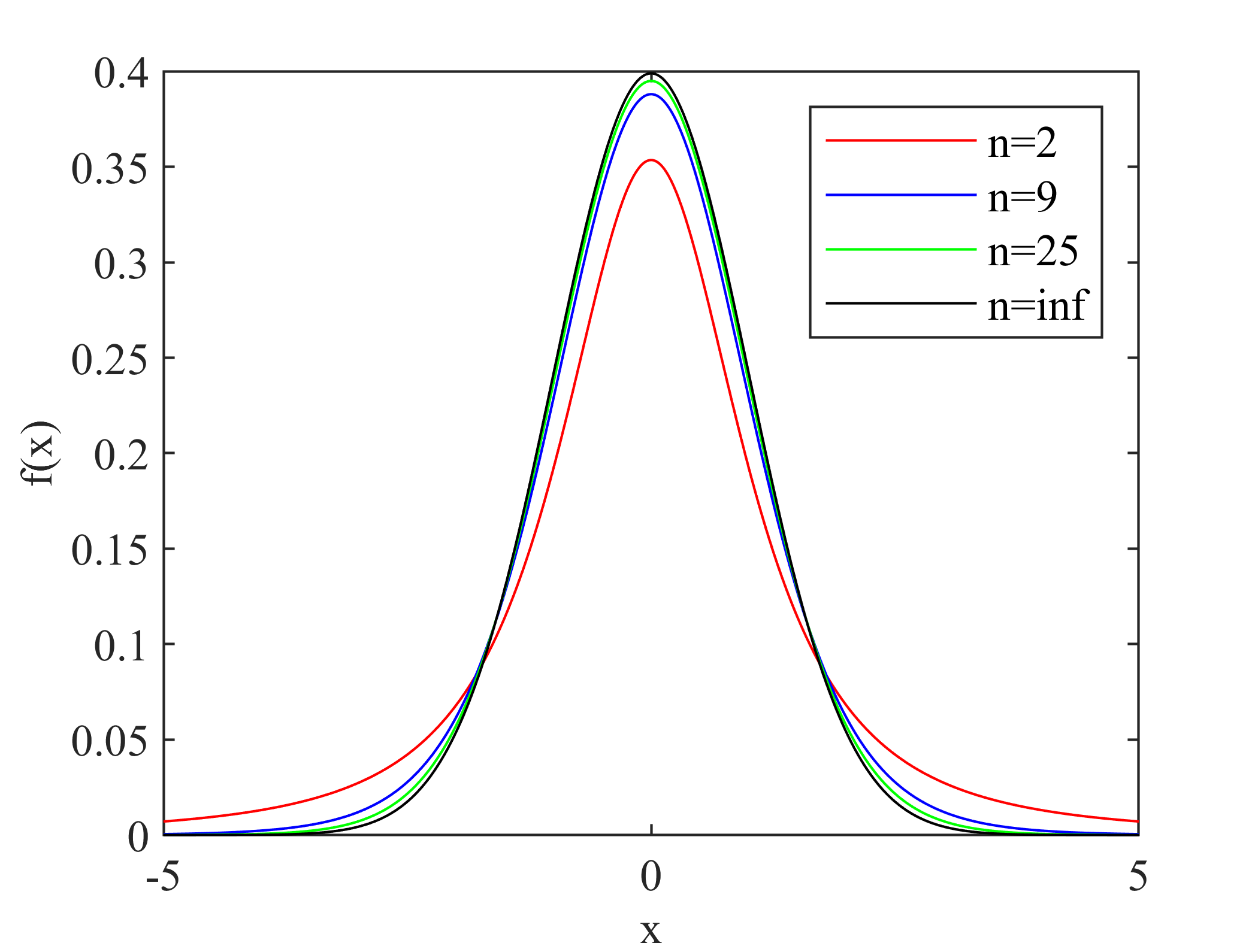
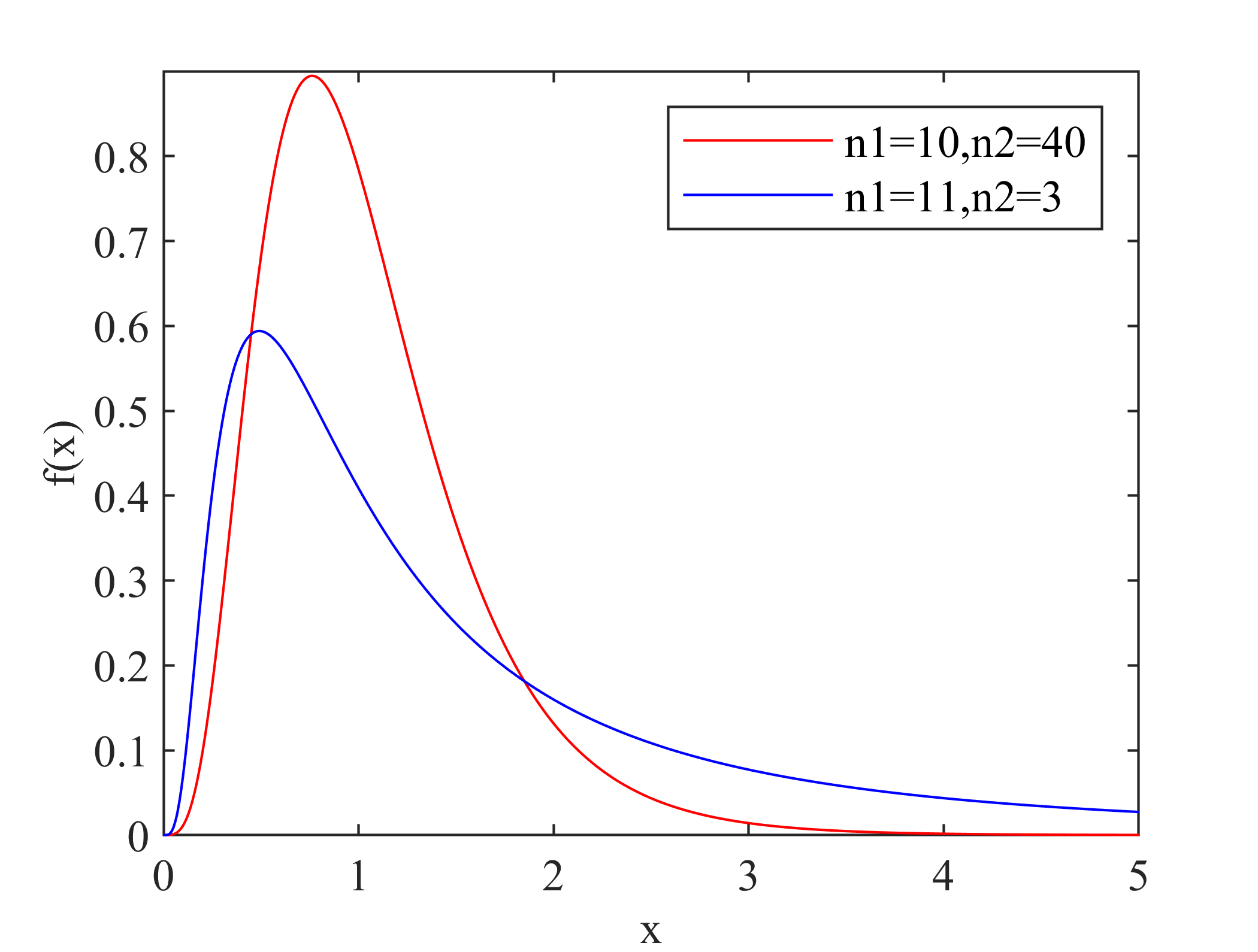
关于上述分布的其他信息可以参考数理统计四大分布---正态分布、卡方分布、学生t分布和F分布





