20172303 2018-2019-1《程序设计与数据结构》第5周学习总结

20172303 2018-2019-1《程序设计与数据结构》第5周学习总结

教材学习内容总结

终于结束了各种不同类型的数据结构的学习，本章的内容转向了对于不同数据结构中存储的数据的处理方面，主要学习了两部分内容——查找和排序，其中查找介绍了两种方法，排序除上学期学过的两种排序方法，又学习了四种新的排序方法。

一、静态方法

  • 静态方法：使用时不需要实例化该类的一个对象，可以直接通过类名来激活的方法。可以通过在方法声明中使用static修饰符将方法声明为静态的。
  • 泛型方法：在方法头的返回类型中有泛型声明的方法。
public class MathTest {
 
    public static void main(String[] args) {
        MathTest mathTest = new MathTest();
        System.out.println(mathTest.max(1, 2));
        System.out.println(mathTest.max(2.0, 3.0));
    }
 
    //泛型方法
    private <T extends Comparable> T max(T t1, T t2) {
        return t1.compareTo(t2) > 0 ? t1 : t2;
    }
    
    //静态泛型方法
    private static <T extends Comparable> T max(T t1, T t2) {
        return t1.compareTo(t2) > 0 ? t1 : t2;
    }
}

二、查找

  • 定义：在某个项目组（查找池）中寻找某一指定元素目标或确定某一指定元素目标不在项目组中。
  • 目标：尽可能高效地完成查找——使过程中所做的比较次数最小化。
    • 决定比较次数的因素：查找的方法，查找池中元素的数目。

1.线性查找

  • 概念：在一个元素类型相同的项目组中，从头开始依次比较每一个值直至结尾，若找到指定元素返回索引值，否则返回false。
  • 时间复杂度分析：最好的情况下是列表的第一个元素就是所要找的指定元素，此时的时间复杂度为O(1)。最坏的情况下，所找元素并不在列表中，那么就需要遍历列表直至尾部终止，这时要进行n次比较，时间复杂度为O(n)。所以，线性查找的平均时间复杂度为O(n)。

2.二分查找

  • 概念：在一个已排序的项目组中，从列表的中间开始查找，如果中间元素不是要找的指定元素，则削减一半查找池，从剩余一半的查找池（可行候选项）中继续以与之前相同的方式进行查找，多次循环直至找到目标元素或确定目标元素不在查找池中。
  • 特点：二分查找的每次比较都会删除一半的元素。
  • 时间复杂度分析：最好的情况是所要查找的元素就位于查找池的中央，此时的时间复杂度为O(1)。当所查找元素不在查找池中时，需要一直削减项目组的一半直至项目组的元素只剩下一个，这种情况下要进行log2n次比较。所以，二分查找的平均时间复杂度为O(log2n)。

3.两种查找方法的比较

  • 在元素个数较小时，两种方法的效率几乎没有区别，但是当元素个数非常多时，二分查找要优于线性查找。
  • 所找元素位置的不同也会影响查找方法的选择，比如在下面这个例子中，当使用线性检索和二分检索求23的位置和检索1的位置时，二者的时间存在差别很大。
  • 使用线性检索和二分检索求23的位置
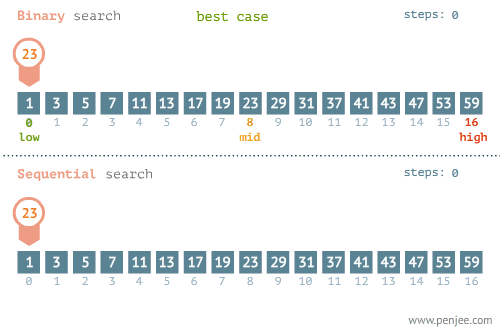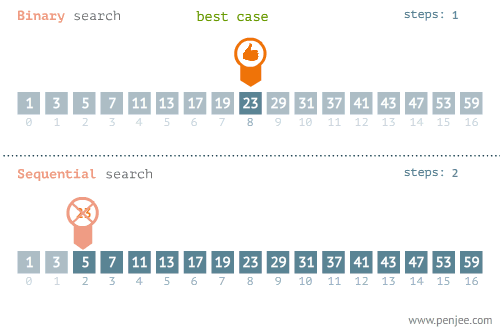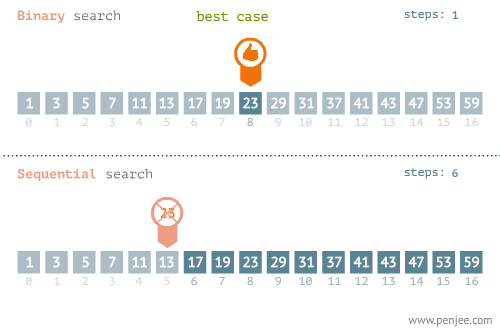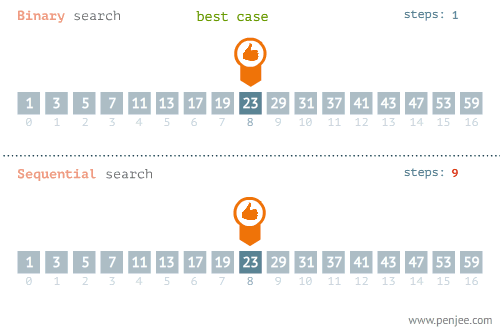
  • 使用线性检索和二分检索求1的位置

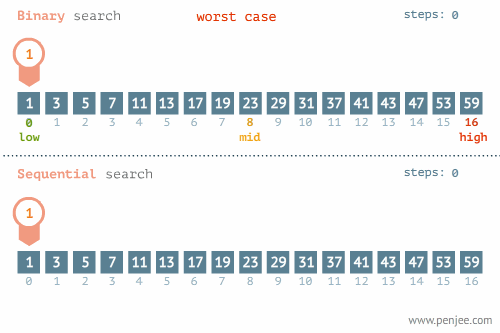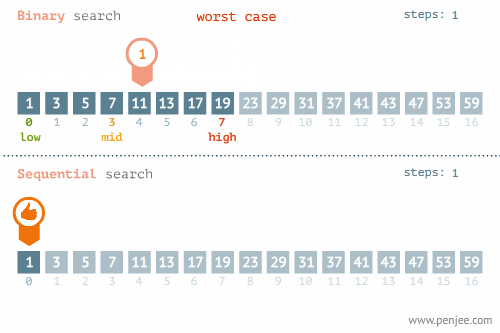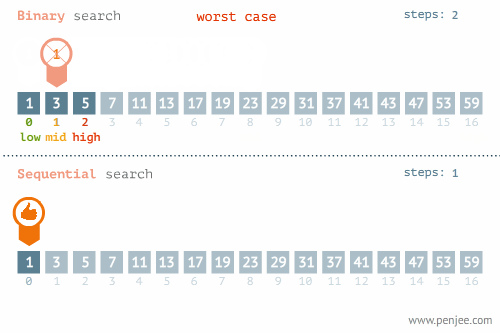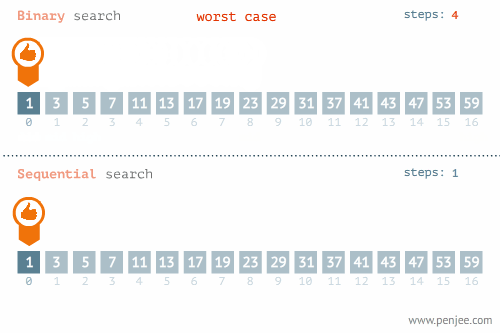
三、排序

  • 概念：基于某一标准，将某一组项目按照某个规定顺序排序。
  • 分类：顺序排序（大概需要n^2次比较）对数排序（大概需要nlog2n次比较）
    • 顺序排序——选择排序、插入排序、冒泡排序
    • 对数排序——快速排序、归并排序
    • 基数排序

三种顺序排序的时间复杂度均为O(n^2)，原因是它们都要通过两层循环来实现，且每层循环都要进行n次，下面主要进行两层循环作用的分析。

1.选择排序

  • 原理：通过反复将某一特定值放到它在列表中的最终已排序位置来实现排序。
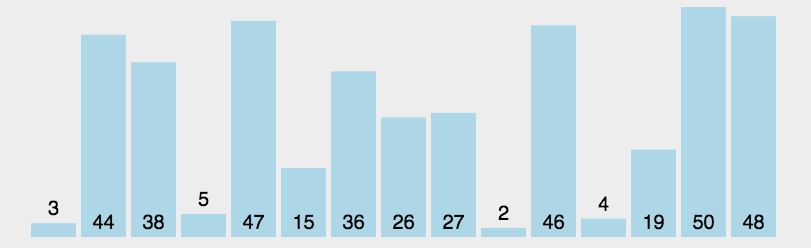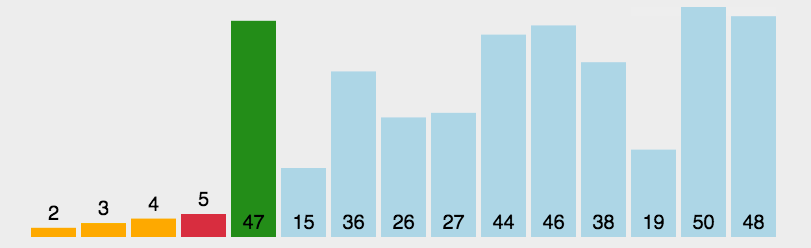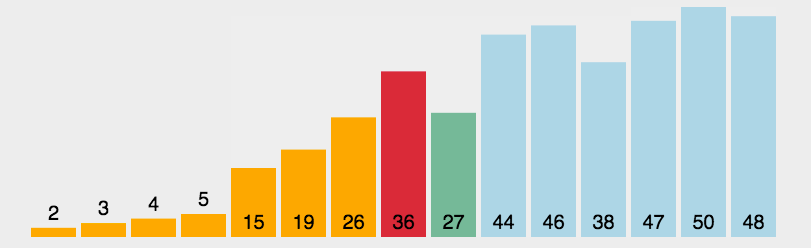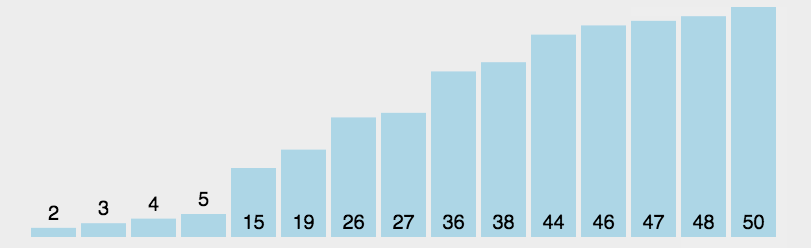
  • 代码分析：选择排序有两层循环，外侧循环控制下一个最值在列表中的存储位置，内侧循环通过遍历和比较来找出剩余列表的最值。
public static <T extends Comparable<T>> void selectionSort(T[] data)
    {
        int min;
        T temp;
        //循环次数为n，时间复杂度为O(n)
        for (int index = 0; index < data.length-1; index++)
        {
            min = index;
            //循环次数为n，时间复杂度为O(n)
            for (int scan = index+1; scan < data.length; scan++) {
				if (data[scan].compareTo(data[min])<0) {
					min = scan;
				}
			}
            swap(data, min, index);
        }
    }

2.插入排序

  • 原理：通过反复将一特定值插入列表中某一已排序的自己中来实现排序。
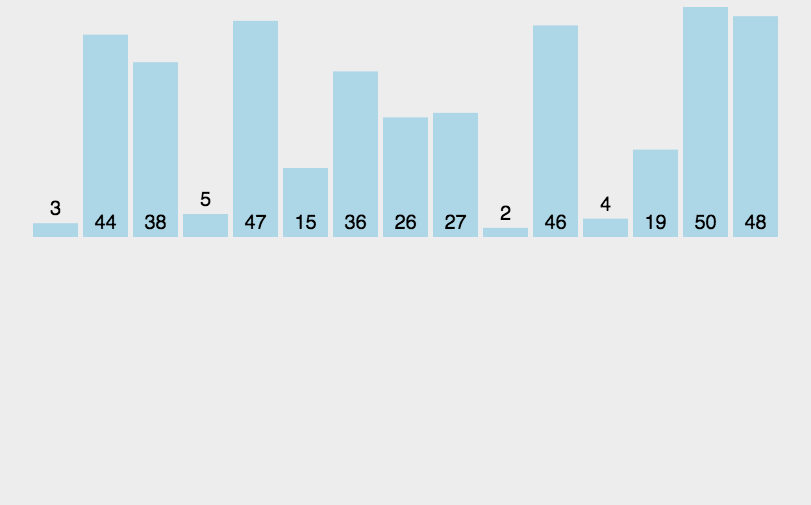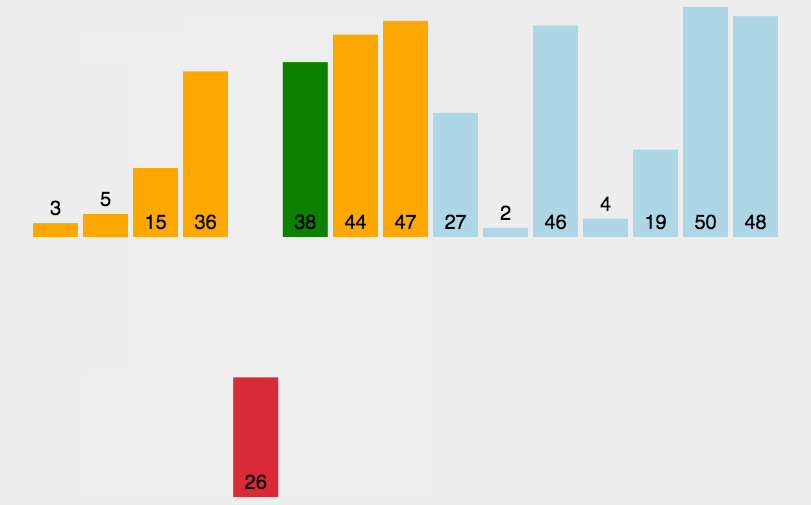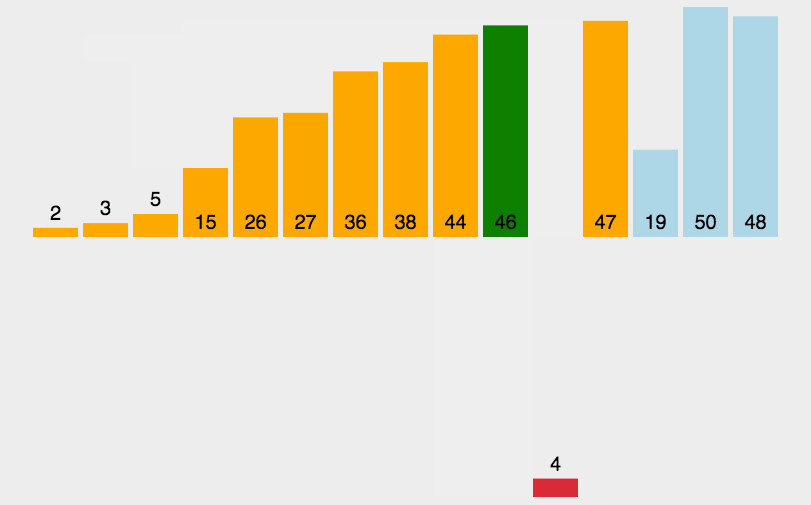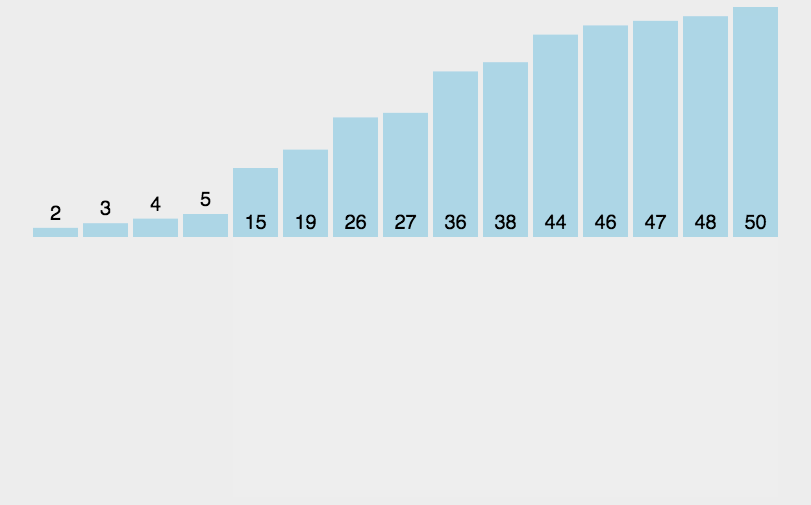
  • 代码分析：与选择排序类似，插入排序也使用了两层循环，外侧控制的是下一个插入值在列表中的位置，内侧循环是将当前插入值与已排序子集中的值进行比较，两者同样都要循环n次。
 public static <T extends Comparable<T>> void insertionSort(T[] data)
    {
        //循环次数为n，时间复杂度为O(n)
        for (int index = 1; index < data.length; index++)
        {
            T key = data[index];
            int position = index;
			
            //循环次数为n，时间复杂度为O(n)
            while (position > 0 && data[position-1].compareTo(key) > 0)
            {
                data[position] = data[position-1];
                position--;
            }
			
            data[position] = key;
        }
    }

3.冒泡排序

  • 原理：通过反复比较相邻元素的大小并在必要时进行互换，最终实现排序。
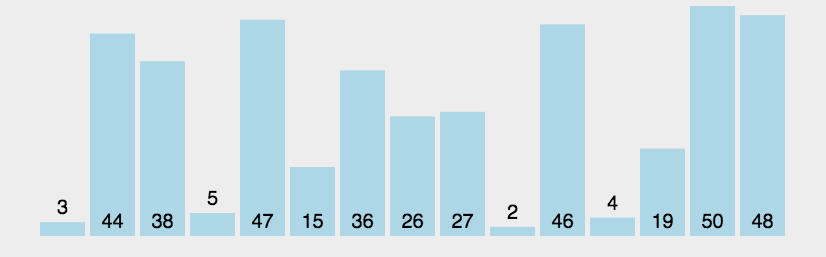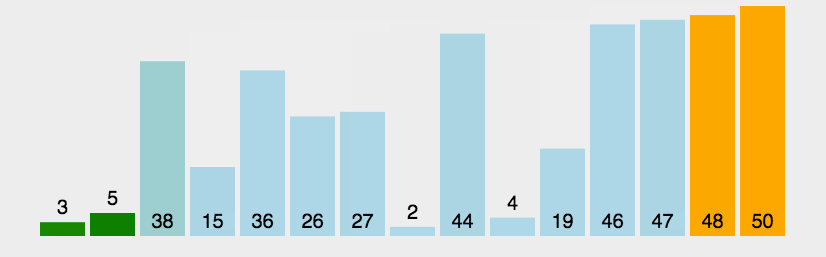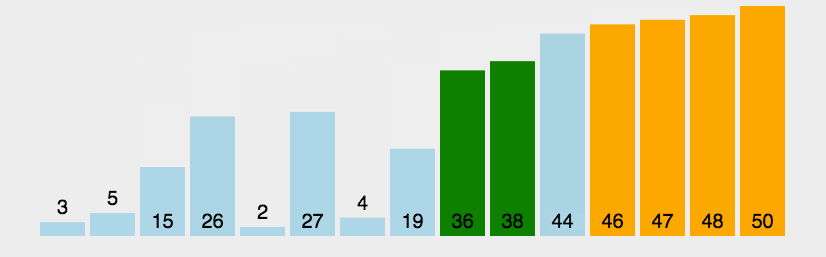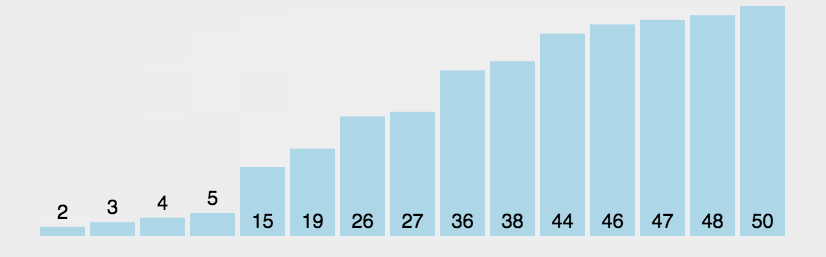
  • 代码分析：冒泡排序的两层循环中，外层循环负责不断进行遍历剩余所有列表（共n-1次），内层循环在每次外层循环的过程中扫描所有相邻元素并依据规则对他们进行互换。
public static <T extends Comparable<T>> void bubbleSort(T[] data)
    {
        int position, scan;
        T temp;
		//循环次数为n-1，时间复杂度为O(n)
        for (position =  data.length - 1; position >= 0; position--)
        {
            //循环次数为n，时间复杂度为O(n)
            for (scan = 0; scan <= position - 1; scan++)
            {
                if (data[scan].compareTo(data[scan+1]) > 0) {
					swap(data, scan, scan + 1);
				}
            }
        }
    }

快速排序和归并排序的平均时间复杂度相同，都是O(nlogn)。

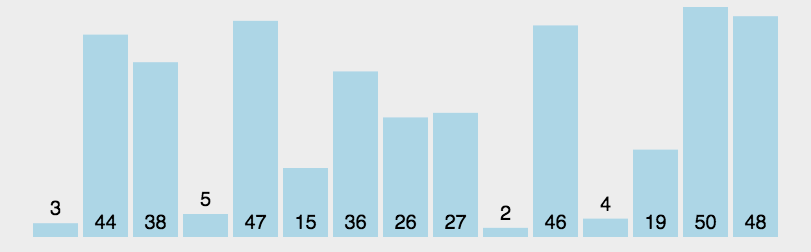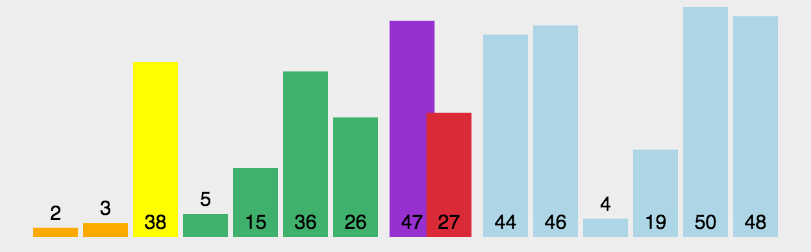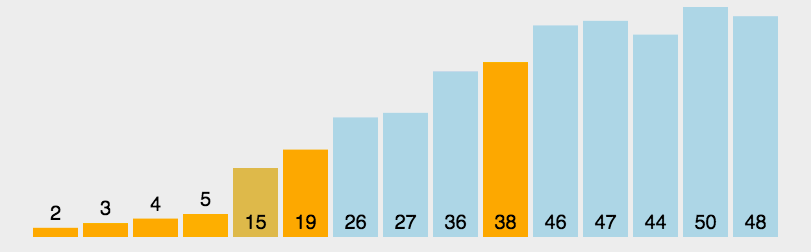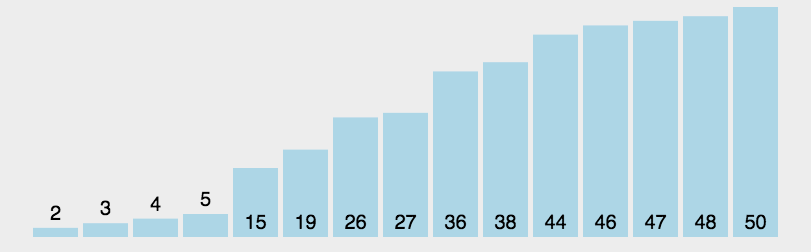
4.快速排序

  • 原理：通过将列表进行分区，对两个分区内的数据进行递归式排序。
    • 递归：用一句简单易懂的话来讲就是——自己调用自己。
  • 代码分析：快速排序本身的代码实现非常简单，就是一个递归的实现。但它其中最核心的方法是使用了一个分区方法partition。
    • 该方法有两层循环，外层循环负责进行每次分区的选择，内层循环中有两个while循环，用于将两个分区中对应位置错误的元素找到并进行交换，直至左索引与右索引相等。
  • 时间复杂度分析：快速排序每次要将列表分成两个分区，因此平均要进行log2n次分区，而每次分区后要进行n次比较操作，因此平均时间复杂度为O(nlogn)。快速排序比大部分排序算法都要快，但快速排序是一个非常不稳定的排序，因为若初始序列按关键码有序或基本有序时，快速排序反而蜕化为冒泡排序，此时它的时间复杂度就为O(n^2)了。

5.归并排序

  • 原理：通过将列表进行递归式分区直至最后每个列表中都只剩余一个元素后，将所有列表重新按顺序重组完成排序。
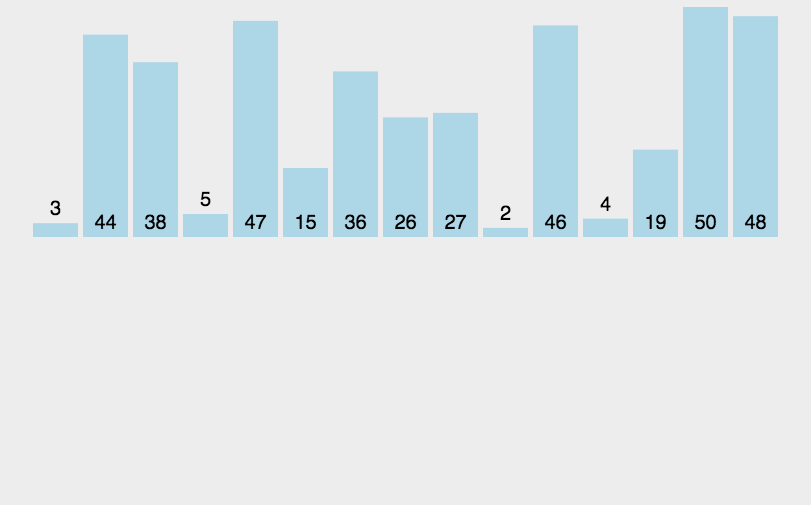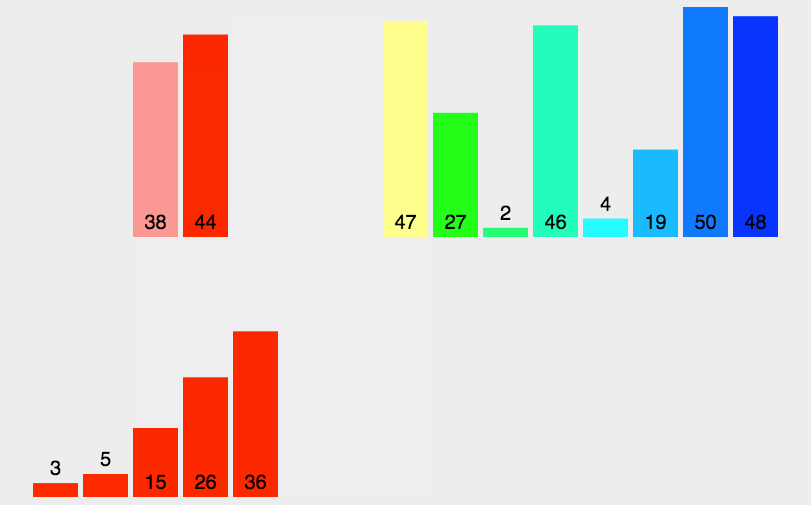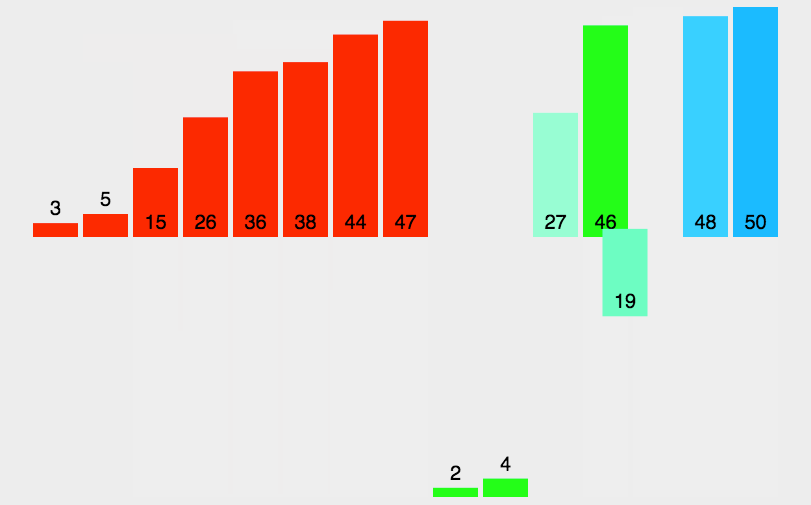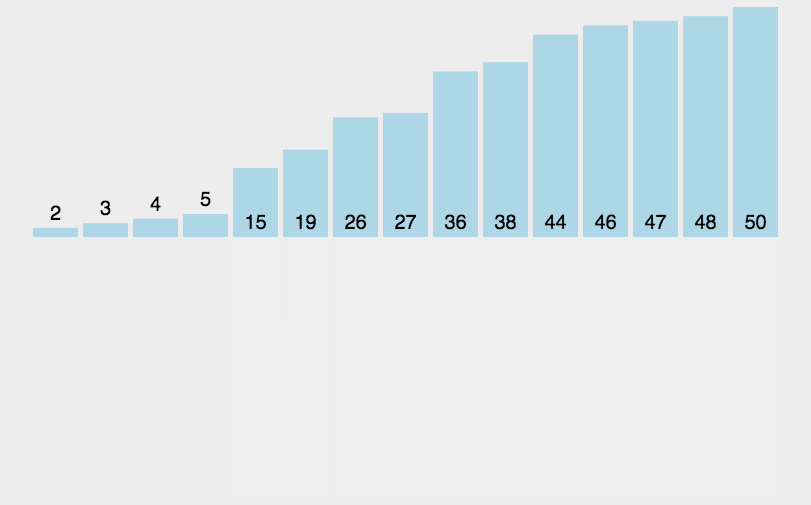
  • 代码分析：和快速排序类似，归并排序本身也是一个递归的实现，但是也使用了一个merge方法来重组数组已排序的部分。
    • merge方法中共有四个循环，第一个while循环将两个子列表中的最小元素分别加入到一个临时的数组temp中，然后第二个和第三个while循环的用处是分别将子列表中剩余的元素加入到temp中，最后一个for循环就是将合并后的数据再复制到原始的数组中去。
  • 时间复杂度分析：每次归并时要将待排序列表中的所有元素遍历一遍，因次时间复杂度为O(n)。与快速排序类似，归并排序也先将列表不断分区直至每个列表只剩余一个元素，这个过程需要进行log2n次分区。因此归并排序的平均时间复杂度为O(nlogn)。

6.五种排序方法对比

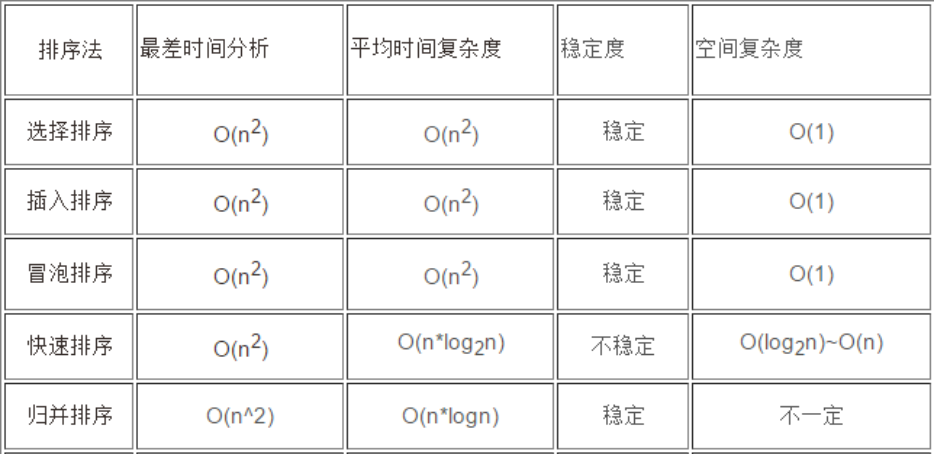
  • 通过对比可以发现，快速排序比大部分排序算法都要快。尽管我们可以在某些特殊的情况下写出比快速排序快的算法，但是就通常情况而言，没有比它更快的了。但是快速排序的稳定性较差，如果需要一个稳定性较好且排序较快的排序算法的话，可以选择使用归并排序，但是归并排序同样存在缺点，因为它需要一个额外的数组，因此对内存空间有一定的要求。

与之前介绍的五种排序方法不同，基数排序法是一种不需要进行元素之间相互比较的排序方法。

7.基数排序

  • 原理：基数排序是基于排序关键字结构来排序的，对于关键字结构中的每一个数字或者字符，都会创建一个单独的队列，而队列的数目就称之为基数。而基数排序法究竟是怎么利用这些队列的，来看看下面的GIF图吧：
  • 时间复杂度分析：在基数排序中，每一个元素都是不断从一个队列中移到另一个队列中，每次都要进行一次遍历，时间复杂度为O(n)，排序的基数有多大，遍历就要进行多少次，但基数的大小只影响n的系数，所以，基数排序的时间复杂度为O(n)。
  • 既然基数排序的时间复杂度这么低，为什么不是所有的排序都使用基数排序法呢？
    • 首先，基数排序无法创造出一个使用于所有对象类型的泛型基数排序，因为在排序过程中要进行关键字取值的切分，因此关键字的类型必须是确定的。
    • 其次，当基数排序中的基数大小与列表中的元素数目非常接近时，基数排序法的实际时间复杂度接近于O(n^2)。

教材学习中的问题和解决过程

  • 问题1：为什么要使用泛型方法？
  • 问题1解决方案：如果你定义了一个泛型，不论是类还是接口，那么Java规定，你不能在静态方法包括其他所有静态内容中使用泛型的类型参数。因此，如果想要在静态方法中使用泛型，就要使用泛型方法了。
public class A<T> {
    public static void B(T t) {
    //报错，编译不通过
    }
}
  • 那么应该如何定义泛型方法呢？
  • 定义泛型方法就像定义泛型类或接口一样，在定义类名（或者接口名）的时候需要指定作用域中谁是泛型参数。
    • 例：public class A<T> {...}
    • 表明在类A的作用域中，T是泛型类型参数。
  • 具体格式是修饰符 <类型参数列表> 返回类型 方法名(形参列表) {方法体}
    • 例：public static <T> int A(List<T> list) { ... }
  • 泛型方法的定义和普通方法定义不同的地方在于需要在修饰符和返回类型之间加一个泛型类型参数的声明，表明在这个方法作用域中谁才是泛型类型参数。
  • 泛型方法的类型参数可以指定上限，类型上限必须在类型参数声明的地方定义上限，不能在方法参数中定义上限。规定了上限就只能在规定范围内指定类型实参，超出这个范围就会直接编译报错。
//正确
<T extends X> void func(List<T> list){ ... }
//正确
<T extends X> void func(T t){ ... }
//编译错误
<T> void func(List<T extends X> list){ ... }
  • 问题2：在某些书上的某些代码中出现的？是怎么回事？
  • 问题2解决方法：?是一种类型通配符，可以代表范围内任意类型。但是“?”泛型对象是只读的，不可修改，因为“?”类型是不确定的，可以代表范围内任意类型。而所有能用类型通配符?解决的问题都能用泛型方法解决，并且泛型方法可以解决的更好。这里有一篇博客对于两者的对比介绍的非常好。
  • 问题3：为什么快速排序法和归并排序法都要先定义一个私有方法，然后再定义一个公用方法来调用私有方法？
  • 问题3解决方法：个人理解是因为快速排序法和归并排序法无法通过只接受数组对象就可以进行排序，但是为了和其他几种方法保持一致，所以就先定义了一个私有方法接受数组对象、最大值和最小值进行排序，然后使用公有方法接受数组对象，在方法内调用私有方法来实现排序。

代码调试中的问题和解决过程

  • 问题1：在完成PP9.2的时候，实现的间隔排序无法正确将数据进行排序

    代码：
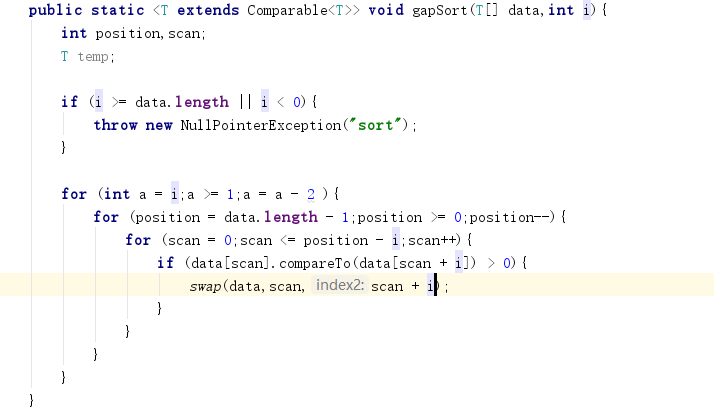
  • 问题1解决方法：通过多次测试之后发现，当输入的数是奇数时排列是正确的，但是当输入的数是偶数时就不行了。原因是由于我设置的每次的减少了为2，当输入的数是偶数时，就会少一次循环过程，因此我对代码进行了修改，增加了对输入的数进行判断，如果输入的是奇数，仍然按原来的方法来，当输入的是偶数时，每次减少的数量为3。
  • 问题2：完成PP9.3时，不论使用什么排序方法输出的执行时间总为0
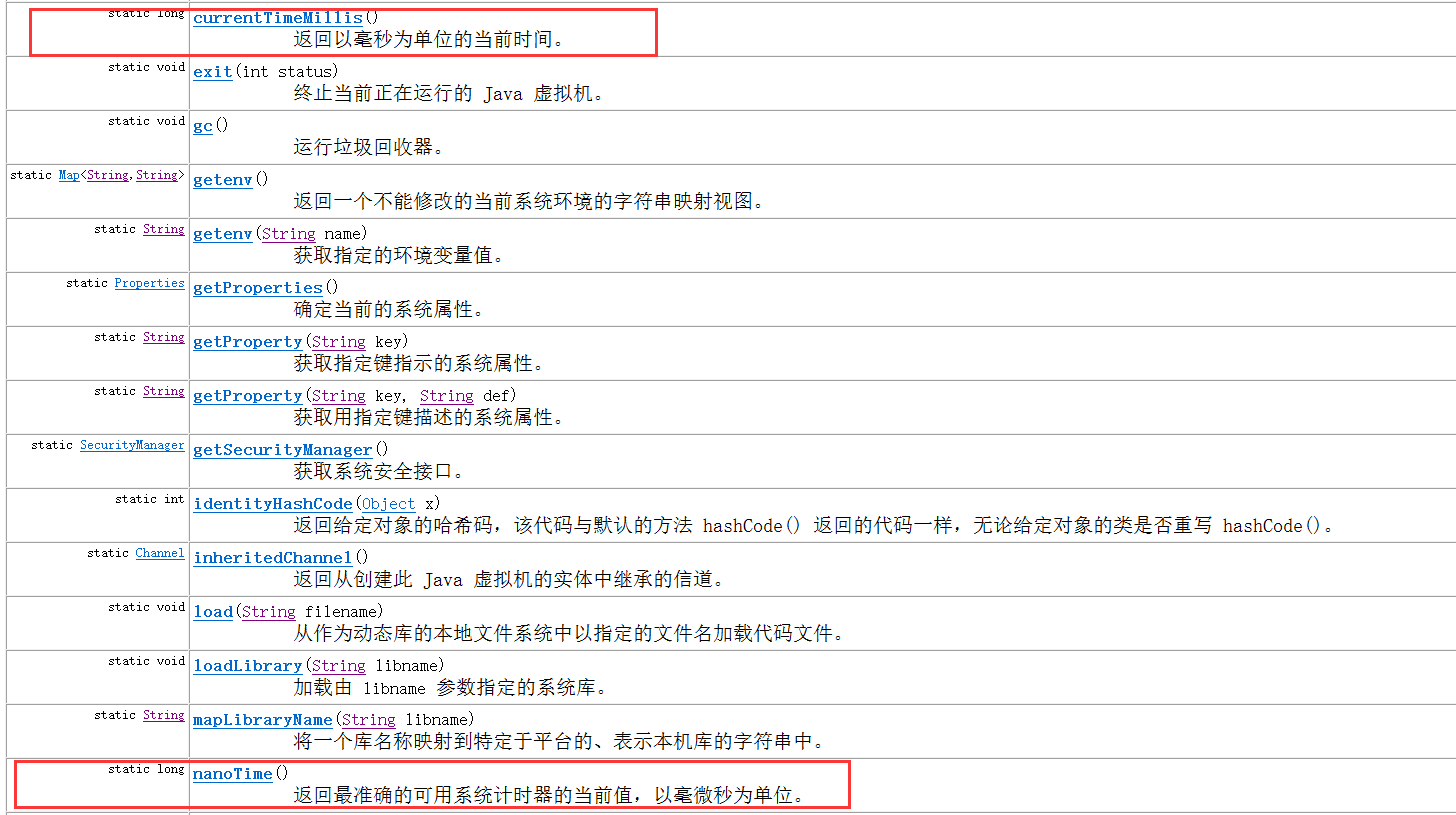
  • 问题2解决方法：一开始我使用的是currentTimeMillis方法，它是以毫秒计时的，而由于排序的元素较少时间还到不了毫秒级，所以显示的都是0，在改成以微秒计时的nanoTime方法后就可以显示了。
  • 问题3：还是在完成PP9.3的过程中，归并排序和快速排序输出了多次比较次数的记录

    代码：
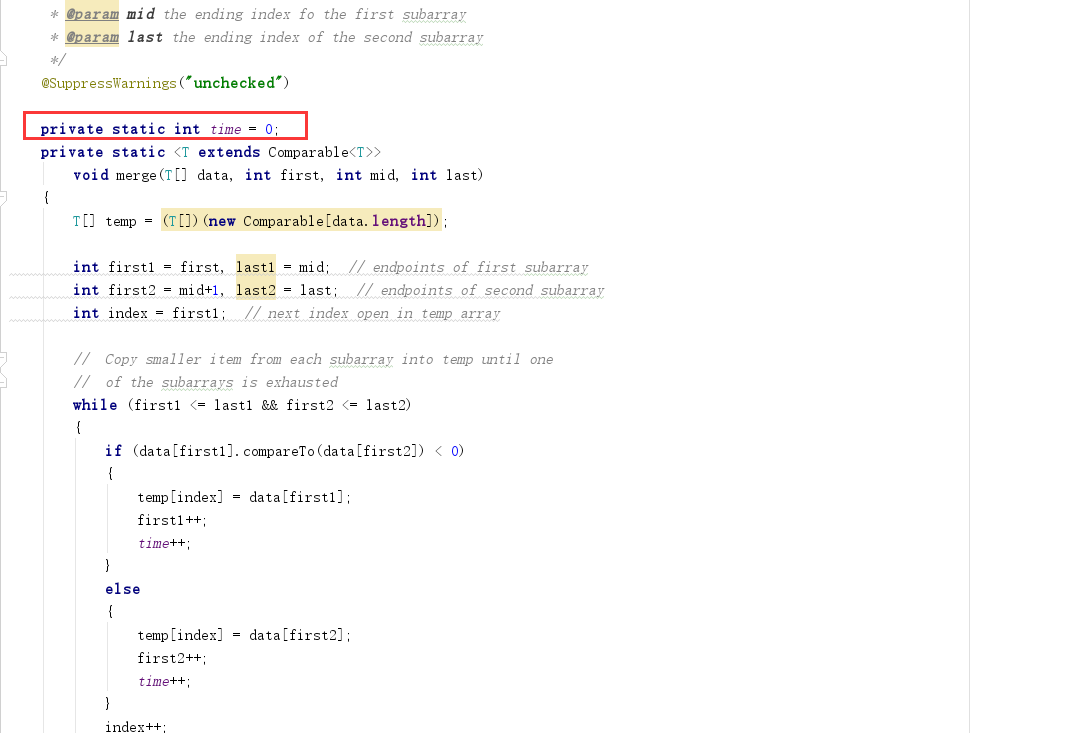
  • 问题3解决方法：虽然我把比较次数的输出写在了merge方法的循环之外，但是在递归的过程中它还是会多次输出。解决方法是将time这个变量放到方法外面去，设置成public static int time = 0即可。

    结果：

代码托管

上周考试错题总结（正确为绿色，错误为红色）

  • 错题1：The Java Collections API contains _________ implementations of an indexed list.
    • A .Two
    • B .Three
    • C .Four
    • D .Five
  • 错题1解决方法：我本来理解的是Java API中提供了几种方法来实现列表，因此选择两种因为一种是ArrayList另一种是LinkedList。后来发现是自己看错题了没有看到“索引”两个字，原话在书上120页。
  • 错题2：The elements of an unordered list are kept in whatever order the client chooses.
    • A .True
    • B .False
  • 错题2解决方法：当时做题的时候想的是无序列表的顺序确实是由使用者来决定的啊，后来想想错误可能出在”whatever"上了。

结对及互评

点评模板：

  • 博客中值得学习的或问题：
    • 优点：本周的博客大有长进！内容丰富了很多，终于做到了图文并茂，值得夸奖！
    • 问题：图片的排版还需加强。
  • 代码中值得学习的或问题：
    • 优点：提了几周的commit提交终于有所改进，感觉这周我的搭档有了质的飞跃。可能是一遍遍的吐槽起了作用，果然像马原老师说的一样，量变会引起质变！
    • 问题：本周代码的备注不是很多。

点评过的同学博客和代码

  • 本周结对学习情况
    • 20172322
    • 结对学习内容
      • 给我讲解了课堂实验ASL计算的方法。
      • 主要探讨了归并排序的计数方法。

其他（感悟、思考等，可选）

  • 因为跳啦啦操的缘故感觉最近的课程总是要落大家一些，现在啦啦操跳完了要赶紧追上大家ヾ(◍°∇°◍)ﾉﾞ

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 10/10 1/1 10/10
第二周 246/366 2/3 20/30
第三周 567/903 1/4 10/40
第四周 2346/3294 2/6 20/60
第五周 1212/4506 2/8 30/90
  • 计划学习时间:20小时
  • 实际学习时间:30小时
  • 改进情况：本周的大部分时间基本都花在了对于查找算法和排序算法的理解上了，感觉对时间复杂度理解和计算的应用变得更加熟练了。

参考资料

posted @ 2018-10-17 19:39  框框框  阅读(409)  评论(3)  编辑  收藏  举报