堆、优先队列、堆排序
可以插入元素和删除最大/小元素的数据类型叫优先队列(以下均为删除最大元素)。
如果用有序数组实现优先队列,易得插入为O(N)(插入排序),删除为O(1);如果用无序数组实现,插入为O(1),删除为O(1)(遍历整个数组)。而用堆实现能够保证插入与删除的时间复杂度都为O(logN)。
一、二叉堆##
在一棵完全二叉树中,如果每个节点都比它的两个子节点大,则这棵完全二叉树是一个二叉最大堆/大根堆,同理有最小堆/小根堆。
堆与二叉排序树最大的不同是在堆中,除了根结点一定是元素中的最大值外,其他节点的元素不是固定的,换句话说,尽管下面这幅图的元素与上图一致,位置不一致,但这也是一个合法的可能的堆:
二、堆的操作##
先来看看插入元素。插入元素的伪代码如下:
把这个元素放在队尾
把队尾元素上浮
删除最大元素的伪代码如下:
把队首元素与队尾元素交换
删除队尾元素
把移到队首的原队尾元素下沉
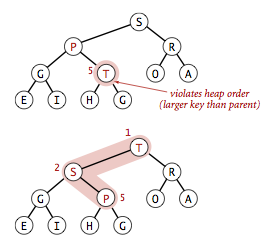
上浮过程非常短,当子结点比父结点大时,互相交换,上溯一层继续比较,直至子结点比父结点小。
void nodeUp(int k) {
for(; k > 1 && PQ[k] > PQ[k >> 1]; k >>= 1)
swap(PQ[k], PQ[k >> 1]);
}
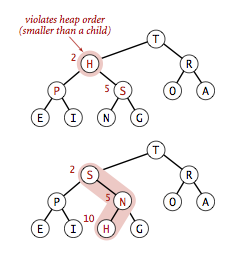
下沉过程写起来长一些,思路是父结点与较大的子结点比较,如果父结点比较大子结点小则交换,在下一层继续比较,直至父结点比两个子结点都大。
void nodeDown(int k) {
int i;
for (; k << 1 <= PQsize; k = i) {
i = k << 1;
if (i < n && PQ[i] < PQ[i + 1])
i++;
if (PQ[i] < PQ[k])
return;
swap(PQ[i], PQ[k]);
}
}
插入与删除最大元素的代码如下
void PQinsert(int v) {
PQsize++;
PQ[PQsize] = v;
nodeUp(PQsize);
}
int PQdelete() {
swap(PQ[1], PQ[PQsize]);
PQsize--;
nodeDown(1);
return PQ[PQsize + 1];
}
三、堆排序##
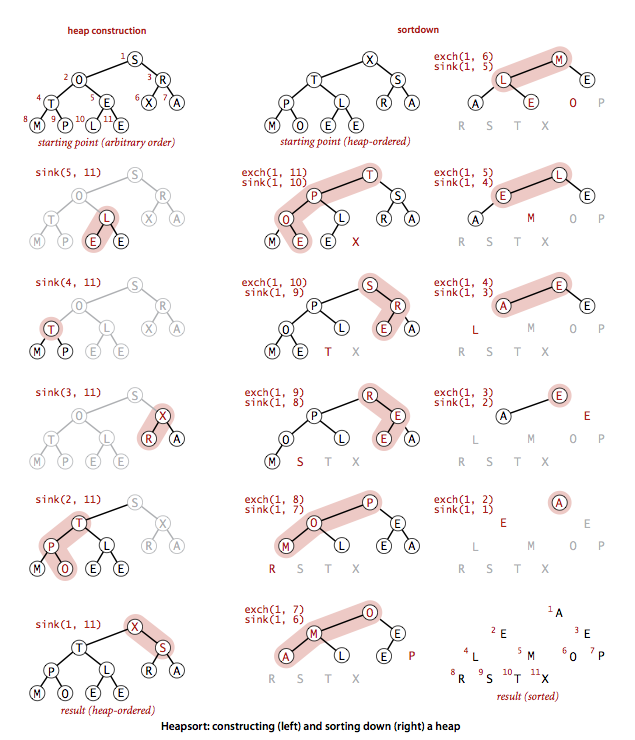
堆排序的方法,其实就是把元素建成最大堆,然后把元素逐个delete。
建堆的过程,就是在数组中逆序下沉所有的分支结点。
主要代码如下
void Heapsort() {
for (i = N >> 1; i >= 0; i--)
nodeDown(i);
for (i = 0; i < N; i++)
PQdelete(); //如果不需要返回值的话不写就好了
}
显然,堆排序的时间复杂度为O(NlogN),空间复杂度为O(1)。堆排序是不稳定的排序算法。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号