树形 DP 笔记 · 一
树形背包
有 \(N\) 个物品，编号分别为 \(1\ldots N\)。物品 \(i\) 的重量为 \(w_i\)，价值为 \(v_i\)。
给出每个物品依赖于哪个物品。我们用 \(d_i = j\) \((i>j>0)\) 表示：如果要选取物品 \(i\)，就必须先选取物品 \(j\)。另外，我们用 \(d_i = 0\) \((i>0)\) 表示：该物品不依赖于任何物品。
背包最多能装载的重量为 \(W\)，请问背包中最多能装入多大价值的物品。
\(O(NW^2)\) 的做法不讲了。\(O(NW)\) 的做法是这样的：先求出一棵树的后序遍历序列 \(ed\)（下文简称后序序列）。比如左下图这棵树，我在右下图中标出了它每个结点的后序。
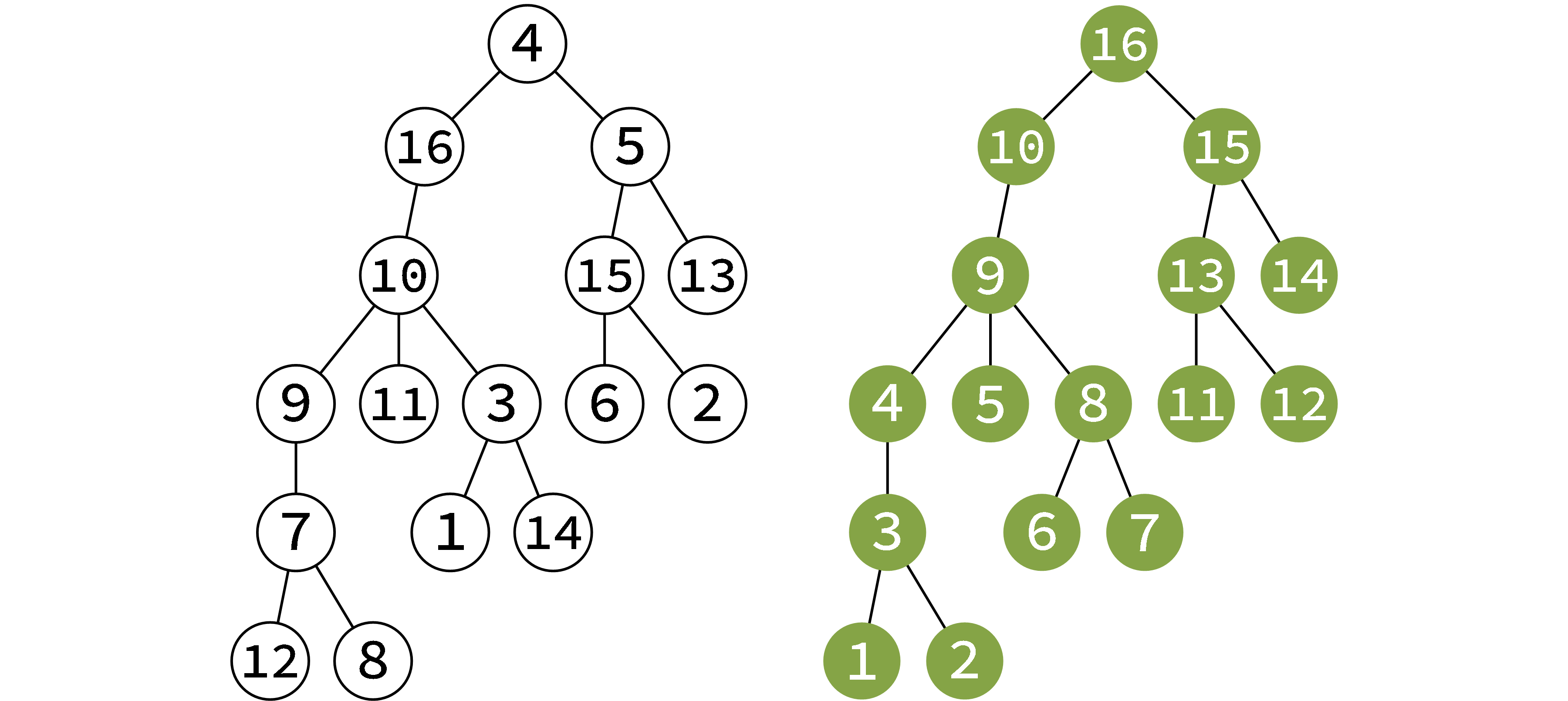
如果我们开一张新的图，然后按照后序序列将结点依次加入图中，我们会发现，每次加入的结点在当前情况下都是根结点。下图展示了放入 4, 7, 8, 9 号结点时，新图的情况。
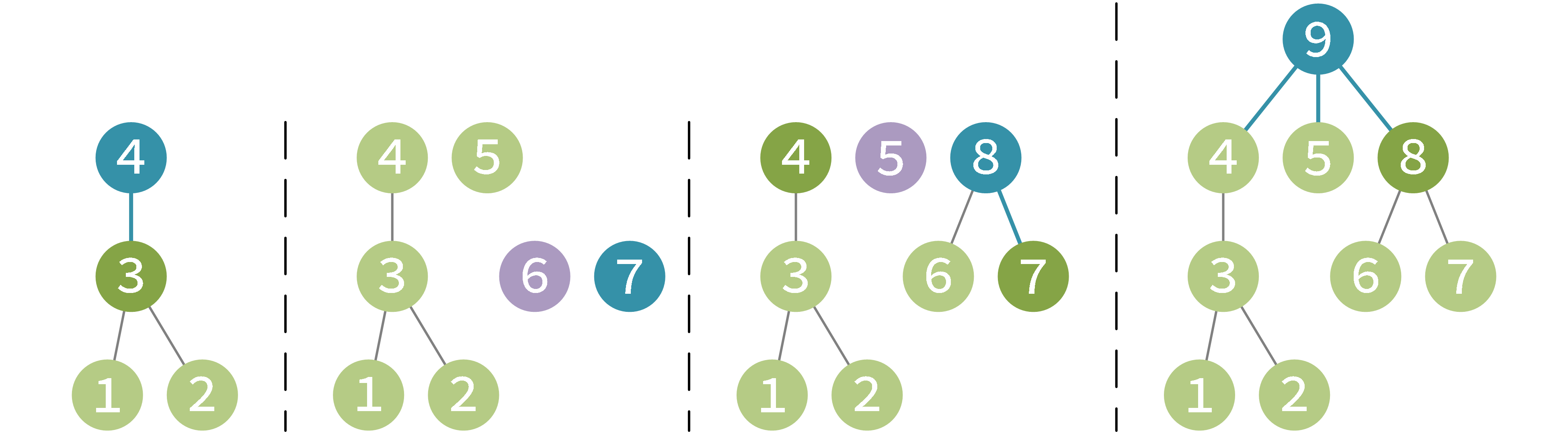
因此，设 \(\mathrm{dp}(i,j)\) 表示将后序序列的前 \(i\) 个结点放入新图，背包容量为 \(j\) 时，所能取得的最大价值。设 \(\mathrm{size}_i\) 以 \(i\) 为根的子树的大小。
- 若取物品 \(i\)（这里以及下文的 \(i\) 均指 \(ed_{?}=i\) 的结点），则可以取它的子树，答案为 \(\mathrm{dp}(i-1,j-w_i)+v_i\)；
- 若不取物品 \(i\)，则答案为 \(\mathrm{dp}(i-\mathrm{size}_i,j)\)；
综上可得 \(\mathrm{dp}(i,j)=\max(\mathrm{dp}(i-1,j-w_i)+v_i,\;\mathrm{dp}(i-\mathrm{size}_i,j))\) 。
Mark
CF815C，CF581F，CF960E，CF633F，CF1065F，CF538E，CF592D，CF461B，CF1088E，CF533B
[Sdoi2017] 苹果树
（NAIPC2018）I - Red Black Tree
Vijos 1676, 1723
