TensorFlow 函数学习笔记
tf.argmax(input, axis=None, name=None, dimension=None)
axis: 0 表示按列，1 表示按行
tf.boolean_mask(a,b)
其中 b 一般是 bool 型的 n 维向量，若 a.shape=[3,3,3], b.shape=[3,3], 则 tf.boolean_mask(a,b) 将使 a(m维) 矩阵仅保留与 b 中“True”元素同下标的部分，并将结果展开到m-1维。
a = np.random.randn(3,3,3)
b = np.max(a,-1)
c = b > 0.5
print("a="+str(a))
print("b="+str(b))
print("c="+str(c))
with tf.Session() as sess:
d=tf.boolean_mask(a,c)
print("d="+str(d.eval(session=sess)))
#输出结果
a=[[[-1.25508127 1.76972539 0.21302597]
[-0.2757053 -0.28133549 -0.50394556]
[-0.70784415 0.52658374 -3.04217963]]
[[ 0.63942957 -0.76669861 -0.2002611 ]
[-0.38026374 0.42007134 -1.08306957]
[ 0.30786828 1.80906798 -0.44145949]]
[[ 0.22965498 -0.23677034 0.24160667]
[ 0.3967085 1.70004822 -0.19343556]
[ 0.18405488 -0.95646895 -0.5863234 ]]]
b=[[ 1.76972539 -0.2757053 0.52658374]
[ 0.63942957 0.42007134 1.80906798]
[ 0.24160667 1.70004822 0.18405488]]
c=[[ True False True]
[ True False True]
[False True False]]
d=[[-1.25508127 1.76972539 0.21302597]
[-0.70784415 0.52658374 -3.04217963]
[ 0.63942957 -0.76669861 -0.2002611 ]
[ 0.30786828 1.80906798 -0.44145949]
[ 0.3967085 1.70004822 -0.19343556]]
c[0,0] = True，则 a[0,0,:] 在结果中保留，c[0,1] = False，则 a[0,1,:] 丢弃，以此类推。
np.reshape() -1
-1 表示根据实际情况自动推测数组剩下的维度
>>> a = np.array([[1,2,3], [4,5,6]])
>>> np.reshape(a, (3,-1)) # the unspecified value is inferred to be 2
array([[1, 2],
[3, 4],
[5, 6]])
np.transpose(a, axes=None)
>>> import numpy as np
>>> a = np.reshape(np.arange(24),[2, 3, 4])
>>> a.shape
(2, 3, 4)
>>> a
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
>>> b = np.transpose(a,[2,0,1])
>>> b.shape
(4, 2, 3)
>>> b
array([[[ 0, 4, 8],
[12, 16, 20]],
[[ 1, 5, 9],
[13, 17, 21]],
[[ 2, 6, 10],
[14, 18, 22]],
[[ 3, 7, 11],
[15, 19, 23]]])
np.transpose 通过 axis 反转输入数组的维度，此程序中原始形状是2个3*4的矩阵，观察结果可见，这个变化是按第三维分成4组，按照第一维（第一维标号是0，1）分成2组，又因为变化后第一维作为横坐标，所以把按第一维分的数据直接列上即可。
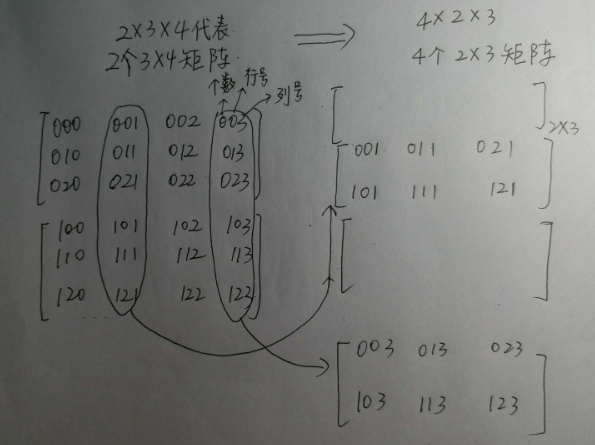
矩阵拼接
tf.concat(values, axis, name='concat')：按照指定的已经存在的轴进行拼接tf.stack(values, axis=0, name='stack')：按照指定的新建的轴进行拼接
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) ==> [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1) ==> [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]]
tf.stack([t1, t2], 0) ==> [[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]
tf.stack([t1, t2], 1) ==> [[[1, 2, 3], [7, 8, 9]], [[4, 5, 6], [10, 11, 12]]]
tf.stack([t1, t2], 2) ==> [[[1, 7], [2, 8], [3, 9]], [[4, 10], [5, 11], [6, 12]]]
上面的结果读起来不太直观，我们从shape角度看一下就很容易明白了：
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) # [2,3] + [2,3] ==> [4, 3]
tf.concat([t1, t2], 1) # [2,3] + [2,3] ==> [2, 6]
tf.stack([t1, t2], 0) # [2,3] + [2,3] ==> [2*,2,3]
tf.stack([t1, t2], 1) # [2,3] + [2,3] ==> [2,2*,3]
tf.stack([t1, t2], 2) # [2,3] + [2,3] ==> [2,3,2*]
tf.pad(tensor,paddings)
tesor 是要填充的张量；paddings 也是一个张量，代表每一维填充多少行/列。
pad_mat = np.array([[0, 0], [pad_size, pad_size], [pad_size, pad_size], [0, 0]])
x_pad = tf.pad(x, pad_mat)
x 是一个四维张量（batchsize, width, height, channels)
