模型评估常用方法
1 模型评估常用方法?
一般情况来说,单一评分标准无法完全评估一个机器学习模型。只用good和bad偏离真实场景去评估某个模型,都是一种欠妥的评估方式。下面介绍常用的分类模型和回归模型评估方法。
分类模型常用评估方法:
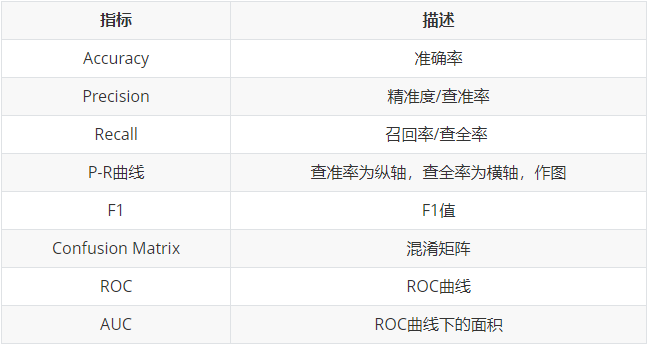
回归模型常用评估方法:
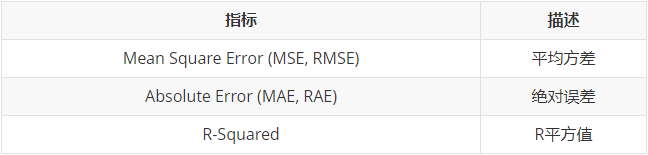
2 混淆矩阵

3 错误率及精度
- 错误率(Error Rate):分类错误的样本数占样本总数的比例。
- 精度(accuracy):分类正确的样本数占样本总数的比例。
4 查准率与查全率
将算法预测的结果分成四种情况:
- 正确归为正样本(True Positive,TP):预测为真,实际为真
- 正确归为负样本(True Negative,TN):预测为假,实际为假
- 错误归为正样本(False Positive,FP):预测为真,实际为假
- 错误归为负样本(False Negative,FN):预测为假,实际为真
则:
查准率(Precision)=TP/(TP+FP)
理解:预测出为阳性的样本中,正确的有多少。区别准确率(正确预测出的样本,包括正确预测为阳性、阴性,占总样本比例)。
例,在所有我们预测有恶性肿瘤的病人中,实际上有恶性肿瘤的病人的百分比,越高越好。
查全率(Recall)=TP/(TP+FN)
理解:正确预测为阳性的数量占总样本中阳性数量的比例。
例,在所有实际上有恶性肿瘤的病人中,成功预测有恶性肿瘤的病人的百分比,越高越好。
5 ROC与AUC
ROC全称是“受试者工作特征”(Receiver Operating Characteristic)。
ROC曲线的面积就是AUC(Area Under Curve)。
AUC用于衡量“二分类问题”机器学习算法性能(泛化能力)。
ROC曲线,通过将连续变量设定出多个不同的临界值,从而计算出一系列真正率和假正率,再以假正率为横坐标、真正率为纵坐标绘制成曲线,曲线下面积越大,推断准确性越高。在ROC曲线上,最靠近坐标图左上方的点为假正率和真正率均较高的临界值。
对于分类器,或者说分类算法,评价指标主要有Precision,Recall,F-score。下图是一个ROC曲线的示例。
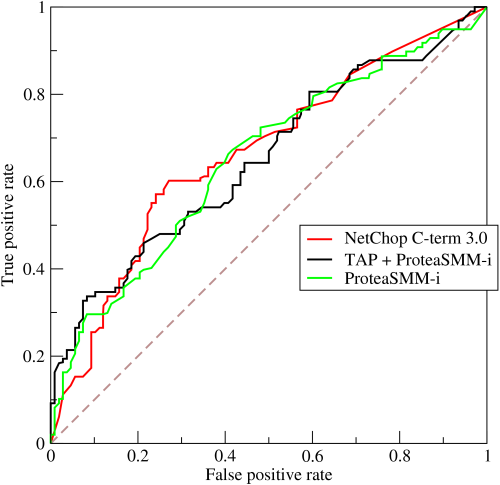
ROC曲线的横坐标为False Positive Rate(FPR),纵坐标为True Positive Rate(TPR)。其中
下面着重介绍ROC曲线图中的四个点和一条线。
第一个点(0,1),即FPR=0, TPR=1,这意味着FN(False Negative)=0,并且FP(False Positive)=0。意味着这是一个完美的分类器,它将所有的样本都正确分类。
第二个点(1,0),即FPR=1,TPR=0,意味着这是一个最糟糕的分类器,因为它成功避开了所有的正确答案。
第三个点(0,0),即FPR=TPR=0,即FP(False Positive)=TP(True Positive)=0,可以发现该分类器预测所有的样本都为负样本(Negative)。
第四个点(1,1),即FPR=TPR=1,分类器实际上预测所有的样本都为正样本。
经过以上分析,ROC曲线越接近左上角,该分类器的性能越好。
ROC曲线所覆盖的面积称为AUC(Area Under Curve),可以更直观的判断学习器的性能,AUC越大则性能越好。
6 如何画ROC曲线
下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。
步骤:
1、假设已经得出一系列样本被划分为正类的概率,按照大小排序。
2、从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。
3、每次选取一个不同的threshold,得到一组FPR和TPR,即ROC曲线上的一点。以此共得到20组FPR和TPR的值。
4、根据3、中的每个坐标点,画图。
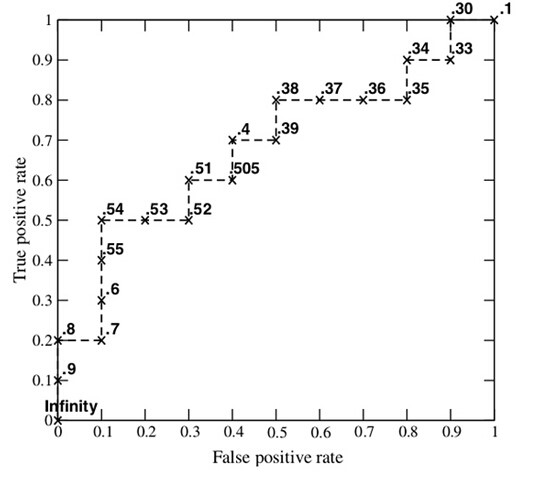
7 如何计算TPR,FPR
分析数据
y_true = [0, 0, 1, 1];scores = [0.1, 0.4, 0.35, 0.8];
列表
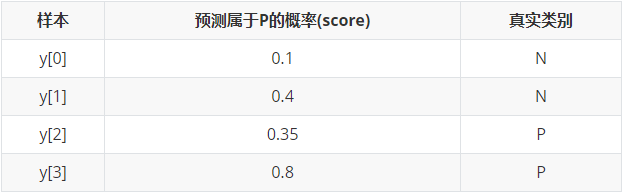
将截断点依次取为score值,计算TPR和FPR
当截断点为0.1时:
说明只要score>=0.1,它的预测类别就是正例。 因为4个样本的score都大于等于0.1,所以,所有样本的预测类别都为P。
scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [1, 1, 1, 1];
正例与反例信息如下:

由此可得:
TPR = TP/(TP+FN) = 1; FPR = FP/(TN+FP) = 1;
当截断点为0.35时:
scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [0, 1, 1, 1];
正例与反例信息如下:

由此可得:
TPR = TP/(TP+FN) = 1; FPR = FP/(TN+FP) = 0.5;
当截断点为0.4时:
scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [0, 1, 0, 1];
正例与反例信息如下:

由此可得:
TPR = TP/(TP+FN) = 0.5; FPR = FP/(TN+FP) = 0.5;
当截断点为0.8时:
scores = [0.1, 0.4, 0.35, 0.8];y_true = [0, 0, 1, 1];y_pred = [0, 0, 0, 1];
正例与反例信息如下:

由此可得:
TPR = TP/(TP+FN) = 0.5; FPR = FP/(TN+FP) = 0;
根据TPR、FPR值,以FPR为横轴,TPR为纵轴画图
8 如何计算AUC
- 将坐标点按照横坐标FPR排序 。
- 计算第\(i\)个坐标点和第\(i+1\)个坐标点的间距\(dx\) 。
- 获取第\(i\)或者\(i+1\)个坐标点的纵坐标y。
- 计算面积微元\(ds=ydx\)。
- 对面积微元进行累加,得到AUC。
9 为什么使用Roc和Auc评价分类器
模型有很多评估方法,为什么还要使用ROC和AUC呢?
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变换的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡,即正负样本比例差距较大,而且测试数据中的正负样本也可能随着时间变化。
10 直观理解AUC
下图展现了三种AUC的值:
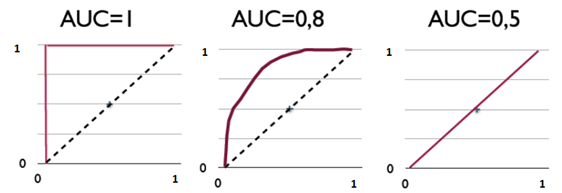
AUC是衡量二分类模型优劣的一种评价指标,表示正例排在负例前面的概率。其他评价指标有精确度、准确率、召回率,而AUC比这三者更为常用。
一般在分类模型中,预测结果都是以概率的形式表现,如果要计算准确率,通常都会手动设置一个阈值来将对应的概率转化成类别,这个阈值也就很大程度上影响了模型准确率的计算。
举例:
现在假设有一个训练好的二分类器对10个正负样本(正例5个,负例5个)预测,得分按高到低排序得到的最好预测结果为[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],即5个正例均排在5个负例前面,正例排在负例前面的概率为100%。然后绘制其ROC曲线,由于是10个样本,除去原点我们需要描10个点,如下:
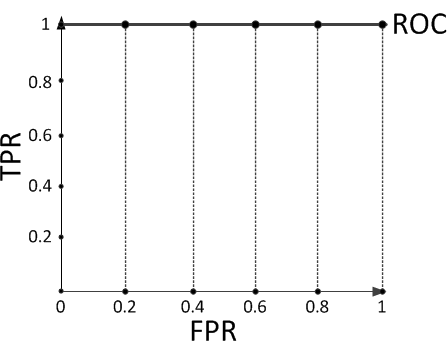
描点方式按照样本预测结果的得分高低从左至右开始遍历。从原点开始,每遇到1便向y轴正方向移动y轴最小步长1个单位,这里是1/5=0.2;每遇到0则向x轴正方向移动x轴最小步长1个单位,这里也是0.2。不难看出,上图的AUC等于1,印证了正例排在负例前面的概率的确为100%。
假设预测结果序列为[1, 1, 1, 1, 0, 1, 0, 0, 0, 0]。

计算上图的AUC为0.96与计算正例与排在负例前面的概率0.8 × 1 + 0.2 × 0.8 = 0.96相等,而左上角阴影部分的面积则是负例排在正例前面的概率0.2 × 0.2 = 0.04。
假设预测结果序列为[1, 1, 1, 0, 1, 0, 1, 0, 0, 0]。
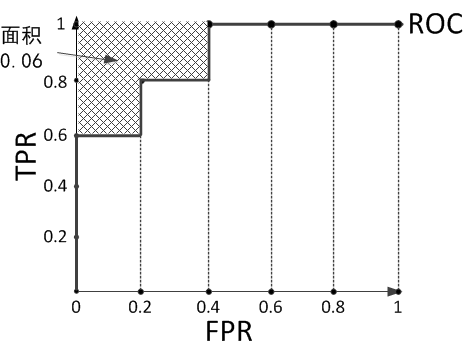
计算上图的AUC为0.88与计算正例与排在负例前面的概率0.6 × 1 + 0.2 × 0.8 + 0.2 × 0.6 = 0.88相等,左上角阴影部分的面积是负例排在正例前面的概率0.2 × 0.2 × 3 = 0.12。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号