基于直方图的图像增强算法

1 对比度和直方图均衡HE

“对比度contrast ratio”这一概念，类似于“动态范围dynamic range”，衡量的是图像中亮区与暗区的比例。

对比度实际上没有统一的测量标准，参见：维基百科 contrast ratio

但我们知道，对比度是影响图像视觉效果的重要因素。

对比度小的图像，其色彩层次少，看起来要么太亮，要么太暗。如下图：

利用MATLAB内置的histeq函数，可以得到对比度增强的图片：

img=imread('View.jpg');
rimg=img(:,:,1);
gimg=img(:,:,2);
bimg=img(:,:,3);
resultr=histeq(rimg);
resultg=histeq(gimg);
resultb=histeq(bimg);
result=cat(3,resultr,resultg,resultb);
subplot(1,2,1)
plot(img);title('原图');
subplot(1,2,2)
plot(result);title('histeq均衡后图');

直方图均衡的本质是灰度值映射。而映射函数可以由分布曲线（累积直方图）得到：

\[D_B = \frac{D_{max}}{A_0}\sum^{D_A}_{i=0}H_i \]

其中 \(A_0\) 是像素总数（图像面积），\(D_{max}\) 是最大灰度值，\(D_A\)、\(D_B\)分别是转换前、后的灰度值，\(H_i\) 是第 i 级灰度的像素个数。

例如原直方图为：

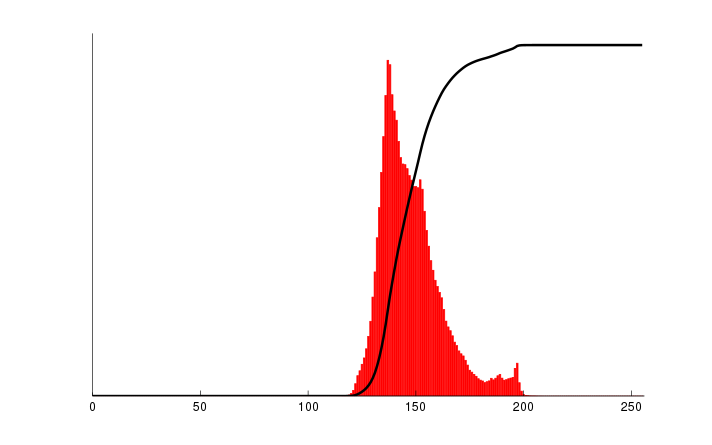
• 灰度值0到120，累积像素个数都为0，因此灰度值0到120都映射到灰度值0；

• 此后黑线开始上升，其纵坐标就是映射到的灰度值（当然还有系数 \(\frac{D_{max}}{A_0}​\) ）。

• 灰度值200左右，黑线饱和，因此其后的灰度值都映射到最大灰度值255。

经过均衡后的直方图为：

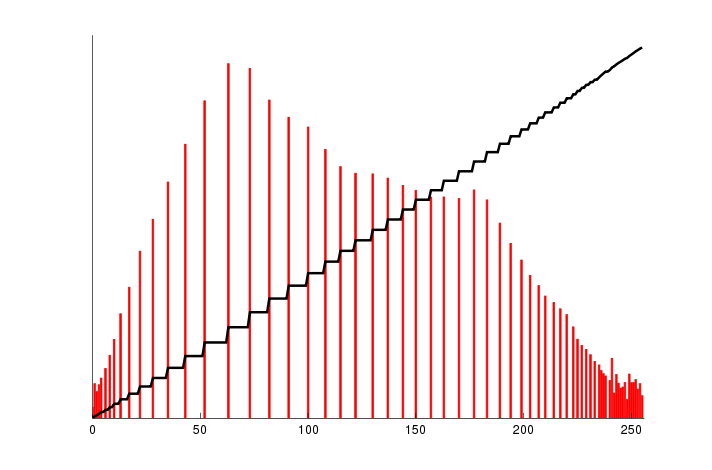
综上，HE后的直方图实际上是原直方图的拉伸，只是左右拉伸程度是变化的，取决于原直方图的幅度变化。

2 HE的问题

以上是直方图均衡Histogram Equalization的简单应用。事实上，HE最初用在医疗图像上。以下图为例：

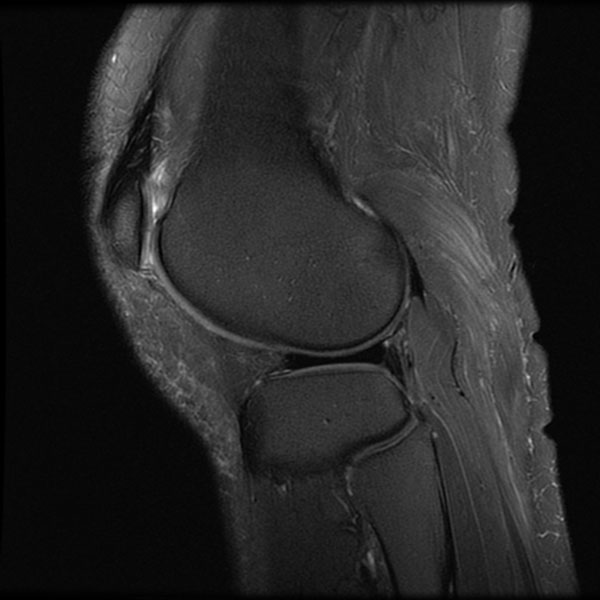
如果只应用简单的HE，结果如图：

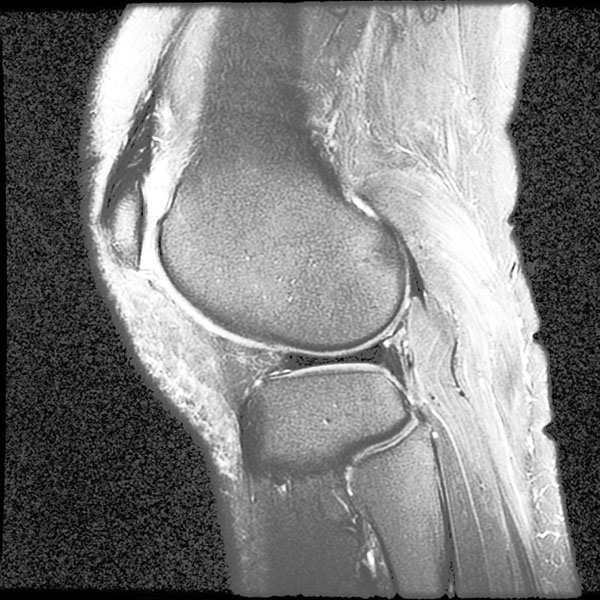
尽管组织“点亮”了，但底噪一样被“点亮”了。

3 AHE

在CLAHE提出以前，学者还提出了自适应直方图均衡Adaptive Histogram Equalization。

AHE的思想很简单：”Since our eyes adapt to the local context of images to evaluate their contents, it makes sense to optimize local image contrast (Pizer et al. 1987).”

大体上是：为了改善局部对比度，我们采用块操作。此时HE在每一个块上都会最优，从而实现各个局部最优。进一步，为了避免边界效应，我们组合块时采用双线性插值法，而不是简单的合并。

根据实验结果，AHE在目标区域表现比HE更出色，但底噪问题仍然没有解决。

4 底噪问题

我们思考一下底噪问题的本质。

不妨考虑极端情况。假设原直方图中只有一个柱子，对应灰度值为0。这就是说，这本应该是一个全黑的块。

然而，根据HE原理，由于灰度值0处的\(D_B = \frac{D_{max}}{A_0}\sum^{D_A}_{i=0}H_i = 255\)，因此灰度值0的柱子变成了灰度值255的柱子。即，全黑图像变成了全白图像。

大斜率导致低灰度值映射到高灰度值，使原本集中的黑色背景“点亮”。因此，我们应该限制分布函数CDF(cumulative distribution function) 的斜率。这就是CLAHE的根本思想。

5 CLAHE

5.1 效果展示

References:
Karel Zuiderveld, “Contrast Limited Adaptive Histogram Equalization”, Graphics Gems IV, p. 474-485, code: p. 479-484

MATLAB内置了adapthisteq函数，可以实现CLAHE算法。我们以Human Knee为例，看看CLAHE效果：

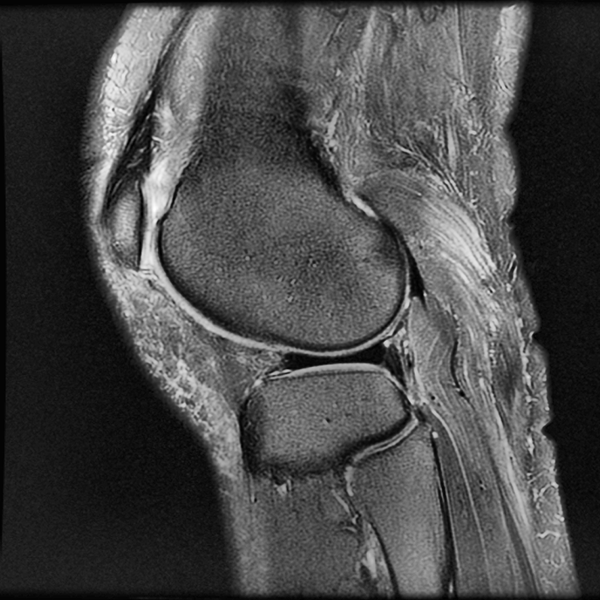
不仅目标被点亮了，而且低噪也被抑制了！

5.2 算法细节

限制CDF的斜率就相当于限制Hist的幅度。

因此我们需要对子块中统计得到的直方图进行裁剪，使其幅值低于某个上限，当然裁剪掉的部分又不能扔掉，我们还需要将这部分裁剪值均匀地分布在整个灰度区间上，以保证直方图总面积不变，如下图：

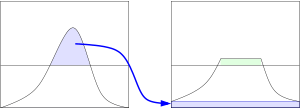
可以看到，这时直方图又会整体上升了一个高度，貌似会超过我们设置的上限。其实在具体实现的时候有很多解决方法，你可以多重复几次裁剪过程，使得上升的部分变得微不足道，或是用另一种常用的方法：

设裁剪值为ClipLimit，求直方图中高于该值的部分的和totalExcess，此时假设将totalExcess均分给所有灰度级， 求出这样导致的直方图整体上升的高度L=totalExcess/N，以upper= ClipLimit-L为界限对直方图进行如下处理：

(1)若幅值高于ClipLimit，直接置为ClipLimit；

(2)若幅值处于Upper和ClipLimit之间，将其填补至ClipLimit；

(3)若幅值低于Upper，直接填补L个像素点；

经过上述操作，用来填补的像素点个数通常会略小于totalExcess，也就是还有一些剩余的像素点没分出去，这个剩余来自于(1)(2)两处。这时我们可以再把这些点均匀地分给那些目前幅值仍然小于ClipLimit的灰度值。

这里给出一段代码：（摘自Matlab的adapthisteq.m），描述的就是上述过程：

% total number of pixels overflowing clip limit in each bin
totalExcess = sum(max(imgHist - clipLimit,0));  
 
% clip the histogram and redistribute the excess pixels in each bin
avgBinIncr = floor(totalExcess/numBins);
upperLimit = clipLimit - avgBinIncr; % bins larger than this will be
                                     % set to clipLimit
 
% this loop should speed up the operation by putting multiple pixels
% into the "obvious" places first
for k=1:numBins
  if imgHist(k) > clipLimit
    imgHist(k) = clipLimit;
  else
    if imgHist(k) > upperLimit % high bin count
      totalExcess = totalExcess - (clipLimit - imgHist(k));
      imgHist(k) = clipLimit;
    else
      totalExcess = totalExcess - avgBinIncr;
      imgHist(k) = imgHist(k) + avgBinIncr;      
    end
  end
end
 
% this loops redistributes the remaining pixels, one pixel at a time
k = 1;
while (totalExcess ~= 0)
  %keep increasing the step as fewer and fewer pixels remain for
  %the redistribution (spread them evenly)
  stepSize = max(floor(numBins/totalExcess),1);
  for m=k:stepSize:numBins
    if imgHist(m) < clipLimit
      imgHist(m) = imgHist(m)+1;
      totalExcess = totalExcess - 1; %reduce excess
      if totalExcess == 0
        break;
      end
    end
  end
  
  k = k+1; %prevent from always placing the pixels in bin #1
  if k > numBins % start over if numBins was reached
    k = 1;
  end
end

CLAHE和AHE中另一个重要的问题：插值。

将图像进行分块处理，若每块中的像素点仅通过该块中的映射函数进行变换，则会导致最终图像呈块状效应：

为了解决这个问题，我们需要利用插值运算，也就是每个像素点出的值由它周围4个子块的映射函数值进行双线性插值得到，如下图：

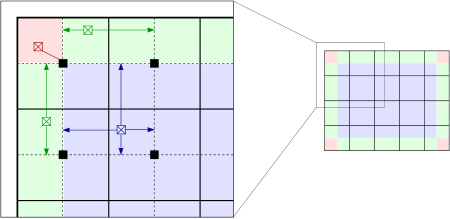
上图中，为了求蓝色像素点处的值，需要利用它周围四个子块的映射函数分别做变换得到四个映射值，再对这四个值做双线性插值即可。

当然对于边界处的像素点则不是通过四个子块进行插值，如上图红色像素点直接以一个子块的映射函数做变换，绿色像素则以两个子块做映射函数做线性插值。这里讲的边界处像素是指落在图像左上角，左下角、右上角，右下角的四个子块中心像素点围成的四边形之外的像素。如下图，将图像分为8x8子块，边界像素即落在灰色区域的像素点。

原文描述如下：

MATLAB内置函数adapthisteq的源代码，函数的输入方式有两种：

J = ADAPTHISTEQ(I)
J = ADAPTHISTEQ(I,PARAM1,VAL1,PARAM2,VAL2...)

参数有：

• NumTiles：是一个[M N]行向量，表征tile的行和列数。默认8x8。最好通过实验确定。
• ClipLimit：0到1的一个标量，表征最大最大clip。显然是归一化的。默认0.01。如果太大，CLAHE退化为AHE。
• NBins：输出图像直方图的柱子个数。因此输入图像和输出图像的位数不一定相同，NBins越大，动态范围越大，但速度越慢。默认为256。
• Range：要么是’original’，要么是’full’。前者限制变换范围在[min(I(😃) max(I(😃)]，后者是整个允许范围。默认为full。
• Distribution：每一个tile的直方图的目标。’uniform’, ‘rayleigh’, ‘exponential’。默认为均衡分布’uniform’。对于水下图片，瑞利分布更自然。
• Alpha：非负标量，在瑞利分布和指数分布时使用。