神经网络训练中的欠拟合、过拟合问题
神经网络训练中的问题
神经网络在数据之海中打捞规律,自成模型。这个过程全权由电脑完成,也因此我们担心它是否是一种泛化的模式,在其它「海域」继续工作时,它能否也能得到正确的结果?如何发现 可以泛化的模式 是机器学习的根本问题。
通常,模型越复杂、训练样本越少,它的泛化能力就会受到考验:
- 可调整参数的数量很多时,模型更容易出现「过拟合」
- 权重参数的取值范围较大时,模型更容易出现「过拟合」
- 训练样本不足时,容易出现「过拟合」(即便模型很简单)
过拟合与欠拟合
我们的数据通常分成3份:
- 训练数据:用于神经网络训练的数据;
- 测试数据:神经网络训练完后,用于评估其准确度的数据;
- 验证数据:为了确定候选模型中的最佳模型所用的检验数据。
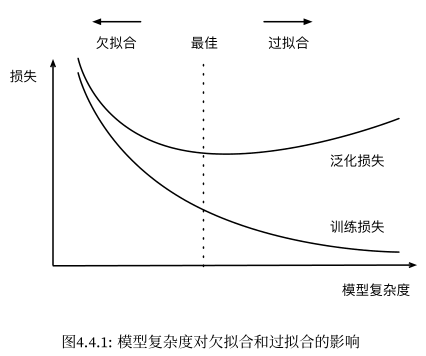
在实际训练中,会有 欠拟合 和 过拟合 的情况。我们将神经网络用训练数据计算时的误差称为「训练误差」,用测试数据计算时的误差称为「泛化误差」。那么:
- 当训练误差与泛化误差都很大时,称模型「欠拟合」。由于训练误差大,所以也称该模型有「高偏差」问题;
- 当训练误差很小,但泛化误差很大时,称模型「过拟合」。由于泛化误差大,所以也称该模型有「高方差」问题。
模型选取
在机器学习中,我们通常从几个候选模型后选择最终的模型。例如,训练多层感知机时,我们会⽐较有着不同隐藏层数、每层有着不同数量神经元以及使用不同激活函数的模型。
当神经网络「欠拟合」时,我们首先可以让它训练更长一段时间,如果仍无效,则会考虑使用更复杂的神经网络(更多隐藏层、增加层的神经元、换其它激活函数等)或者使用其它类型的神经网络。
数据集大小
在如今有大量数据(百万甚至更大)的情况下,训练数据的比重可以占得很大:训/测/验 = 98%/1%/1% 即便是1%的数据也有上万,足以用于检验了,我们可以将更多数据投入训练中。
训练数据集的大小对模型训练结果有什么影响?训练集样本过少,可能会导致严重的「过拟合」问题,反过来说,更多的训练数据能减小泛化误差,而且通常没有坏处(除了训练久一点),尤其是训练复杂的模型时。
在尝试了更多数据后,如果模型仍「过拟合」或者你原本的数据已经是高质量的了,无法再获得更多数据时,则可以考虑 正则化 ,或者换用其它类型的神经网络。
正则化
有一些常用的正则化模型的技术,可以帮助我们缓解过拟合问题。
1. 权重衰减
权重衰减,也称为 \(L_2\) 正则化,它在原本损失函数的基础上,加上了「某系数 * 权重矩阵的各元素平方和」,这个「某系数」一般取较小值(<0.1):

关于该公式的更多内容可以移步这个视频!
从新的损失函数可以看出,如果想要将其值变小,就需要额外将权重的值变小才行。这也就与开头说的影响模型泛化的因素之二(权重取值范围)相吻合,所以它在提高模型泛化能力上能起作用。
- 为什么用 \(L_2\) 而不是 \(L_1\) 正则化?
\(L_2\) 会对权重向量的大分量施加巨大的惩罚,使得学习算法偏向于在大量特征上均匀分布权重的模型。假设有一个神经网络的权重为 \(W = [0.5, 1.2, 1.3, -2.1]\),在进行权重衰减时,首当其冲的必定是-2.1这个值,这有助于防止模型过分依赖该权重计算,使学习算法更倾向于在许多特征上均匀分布权重的模型。 - 需要对偏置b进行同样处理吗?
不需要,因为偏置之于模型,相当于常数至于函数,在函数中调整常数项的大小只会影响函数的位置,并不影响函数的形状;这对于神经网络同理,「泛化能力」与神经网络所构成的函数形状密切相关,所以偏置没必要进行同样的衰减。
2. 暂退法(Dropout)
暂退法会在训练时(具体点说是前向传播时),将模型隐藏层中的每层的神经元以一定概率舍弃:
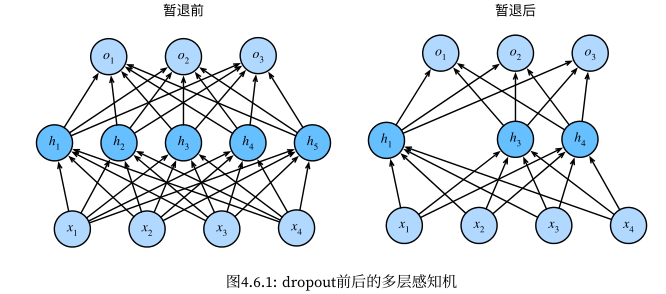
你肯定也能看出它的道理:降低模型复杂度、减小权重参数范围,这分别对应先前所讲的因素一和因素二。
- 降低模型复杂度可以理解,但为什么这么做也能减小权重参数范围?
因为每个权重都有可能被暂时丢弃的可能,也就是说会不参与某几次权重更新,这样也就减小了它的参数范围(相比不做Dropout正则化时)。
参考(墙裂推荐捏):


