第三章:通过搜索进行问题求解
第三章: 通过搜索进行问题求解
本章将讨论基于目标的Agent中的一种,称为 「问题求解Agent」 ,问题求解Agent使用原子表示:世界状态被视为一个整体。
1. 问题求解Agent
基于当前的情形和Agent的性能度量进行 「目标形式化」 是求解问题的第一步。我们将目标考虑成是世界的一个状态集合——目标被满足的那些状态的集合。Agent的任务是找出现在和未来如何行动,以使它达到一个目标状态。「问题形式化」 是在给定目标下确定需要考虑哪些行动和状态的过程,问题的解将是一个行动的固定序列,为达到目标,寻找这样的行动序列的过程被称为 「搜索」 。
简单的问题求解Agent它首先对目标和问题进行形式化,然后搜索能够解决该问题的行动序列,最后依次执行这些行动。这个过程完成之后,它会形式化另一个目标并重复以上步骤。
一个问题可以用5个组成部分形式化地描述:
- Agent的 初始状态。
- 描述Agent的可能 行动。
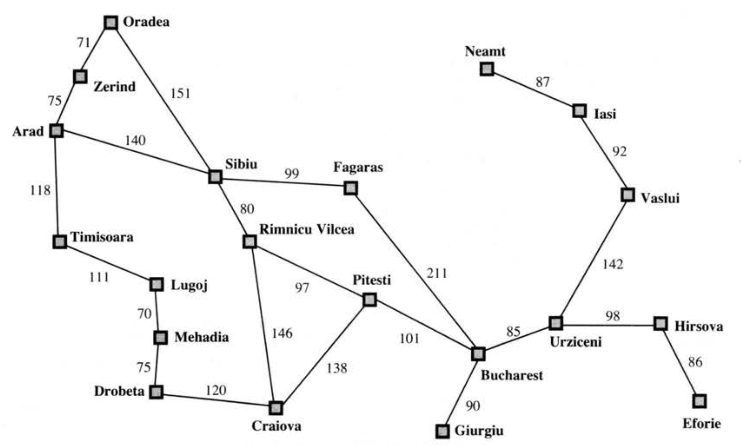
- 对每个行动,它都能在执行后,将一个状态转移到另一个状态,所以,行动的描述也称为 「转移模型」。它与初始状态、行动一起定义了问题的 「状态空间」,状态空间是一个有向图,结点表示状态,边表示行动。
-
- 目标测试,确定给定状态是不是目标状态。有时目标状态是一个显式集合,测试只需简单检查给定的状态是否在目标状态集合中。
- 路径耗散函数为每条边赋一个加权值,问题求解Agent选择能反映它自己的性能度量的耗散函数。
由上述元素即可定义一个问题,问题的解就是从初始状态到目标状态的一组行动序列。解的质量由路径耗散函数度量,所有解里路径耗散值最小的解即为最优解。
我们已经给出了问题的形式化,但它终究是个模型,与现实不同。所以我们需要抽象,不仅是状态描述要抽象,还要对行动进行抽象。如果我们能把任何抽象解扩展成为更细节的世界中的解,这种抽象就是有效的。
(后面作者有列举一些问题实例,比如八数码问题、八皇后问题等,我就略过啦)
2. 通过搜索求解
一个解是一个行动序列,所以搜索算法的工作就是考虑各种可能的行动序列。
而搜索算法的基本结构就是熟悉的(如果学过数据结构与算法基础的话)树搜索。区别主要在搜索策略。搜索策略可分为两大类,一种是 「盲目搜索」,另一种是 「启发式搜索」。
为了更好的表达,我们称寻找下一个结点的行为为 「扩展」。
3. 盲目搜索
所谓盲目搜索,就是除了问题中给的信息以外,不再携带其它任何信息的搜索,这种搜索方式更像是种暴力穷举。
它包含以下几种:
- 广度优先搜索(BFS)
- 一致代价搜索,是广度优先搜索的变种。它将原本无规律的扩展策略,改为了「路径消耗小」优先扩展(增加一个优先队列就可以做到)
- 深度优先搜索(DFS)
- 深度受限搜索,是深度优先搜索的变种。我们对搜索的深度(次数)进行限制,在超过指定深度界限后就停止搜索。这是为了避免过多搜索但毫无结果的情况。
- 迭代加深的深度优先搜索,通常配合深度优先搜索来确定最好的深度界限。做法就是不断加大深度限制,直到搜到为止。这种搜索时间复杂度没想象中那么大——和广度优先搜索差不多,当搜索范围很大但不知道解所在深度时,它是首选的盲目搜索。
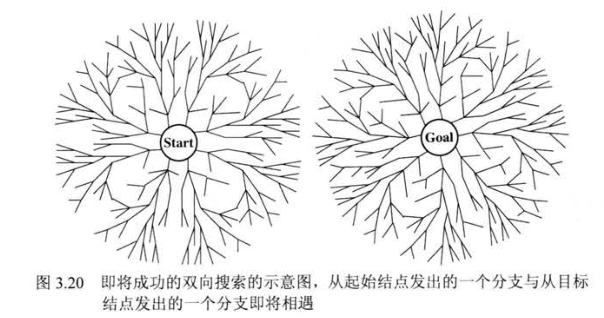
- 双向搜索,就是起点往终点搜的同时,终点也往起点搜,直到二者搜索范围有交集。(但并非适用所有的搜索情况,有时会适得其反)
4. 启发式搜索
启发式搜索使用了问题本身之外的特定知识,它能比盲目搜索更有效地解决问题。大多启发式搜索算法都会有个用于评价的启发函数 \(f(n)\)。还有个启发函数 \(h(n)\):
我们将讨论以下两种搜索方式:
- 贪心最佳优先搜索:试图扩展离目标最近的结点,理由是可能可以很快找到解,所以它的评价函数其实就是启发函数,即 \(f(n)=h(n)\)。
- A*搜索:最广为人知的启发式搜索,它的评判函数结合了 \(g(n)\),也就是「起点结点到当前结点 \(n\) 的路径代价」。所以 A*搜索的评估函数 \(f(n) = g(n) + h(n)\)。令人满意的是,A*搜索在所有此类算法种是完备的、最优的也是效率最优的。但A*并不是完美的,这对于具有大型状态空间的问题它可能需要花费较长的计算时间才能找到最优解;评价函数的需要,使它得存储大量结点,在大规模问题中常会在计算完之前就耗尽内存。
- 存储受限的启发式搜索:
- IDA*算法:和迭代加深的思想一样,也为A*设置一个搜索的界限 \(f(n)\),我们称其为IDA*算法。
- 递归最佳优先搜索(RBFS)算法:RBFS的关键思想是使用递归方法来探索搜索树,而不需要在内存中维护完整的搜索树。它通过动态地更新 \(f_{limit}\) 来控制搜索过程,使得在有限的内存条件下仍能找到最佳解。RBFS会在递归回溯时,为途径的每个结点记录 \(f_{limit}\),该值记录的是当前结点的最小价值 \(f(n)\) 叶结点的值。
IDA*和RBFS的问题在于它们保留的信息太少了,可能会出现某些状态重复扩展多次。所以,充分利用内存是明智的,例如内存受限的(MA*)和简化的MA*(SMA*)。SMA*算法的关键思想是使用有限的内存,在搜索过程中不断更新和回溯。如果内存用尽,就会选择丢弃最差的叶节点,即具有最高启发式函数值的结点。以便在内存受限的条件下找到最佳路径。
它有时可以在有限内存条件下找到最佳解决方案,但对于一些极为复杂的问题,SMA*算法可能会在候选解路径之间来回切换,导致重复生成相同节点,从而增加了计算时间。
上述那些搜索策略,我猜你多多少少在别的地方也听说过,甚至是学过了。这些是早已存在的搜索策略了,那Agent可以自己学习如何更好地搜索吗?当然可以! 「元学习」 算法可以从经验中学到怎么避免搜索没有希望的子树。但这些内容会在以后才讲。
5. 启发式函数
启发式搜索算法的性能取决于启发式函数的质量。好的启发式有时可以通过 「松弛问题」 的定义来构造,将子问题的解代价记录在模式数据库中,或者通过对问题类的经验学习得到。


