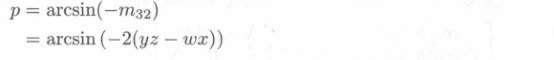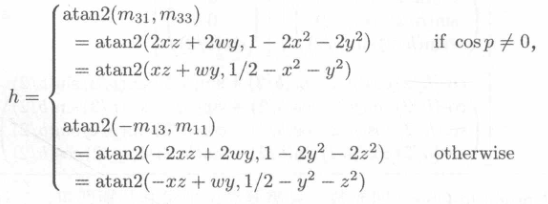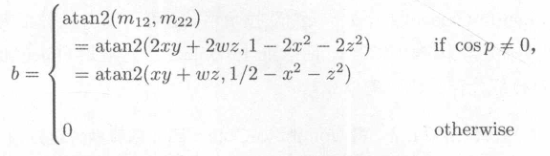第八章：三维旋转

本章我们将来看看不同的表示三维中方向和角位移的方式。它们各有优缺点，我们需要知道它们的原理以及它们之间的转换。

1.“定向”含义探微

有些词和“定向”类似，比如：方向、角位移、旋转。
方向是由球面坐标的两个角度所设置的，而定向则至少要三个数字（就是欧拉角，后面会讲）；而角位移的描述在数学上与定向等同，但本书做了细微的区分，我们将“定向”视为一个状态，“角位移”视为一个过程（就像“点”和“矢量”的区别）。例如：“直立，面向东方”就是定向，“直立，朝东，然后绕z轴旋转\(90^\circ\)”就是角位移。

2.矩阵形式

1. 矩阵形式介绍

当一组基矢量组成了矩阵时，就是用矩阵形式表示了定向。这和先前学习的旋转矩阵相似，只不过将它视为状态而不是变换，就不多说了。

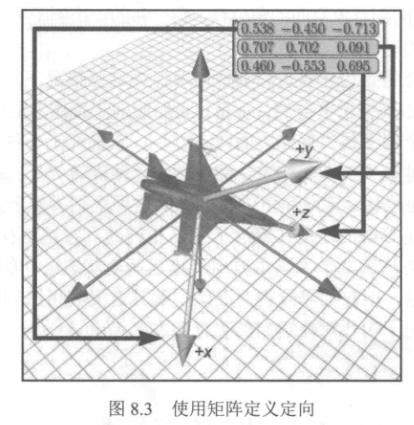
2.矩阵形式的优点

可以仅乘上矩阵就达成旋转或空间坐标的转换，其它的定向方式要旋转矢量，都得先转换成矩阵形式。
适用于图形API，图形API就是使用矩阵形式表示定向的。
方便将多个旋转进行连接。毕竟矩阵可以嵌套坐标系，根据矩阵乘法结合律的性质，可以将多个旋转矩阵合并成一个旋转矩阵。
矩阵求逆。由于旋转矩阵是正交的，我们可以仅通过转置就求得逆矩阵，有了逆矩阵，我们可以很方便执行“反向”的角位移。

3.矩阵形式的缺点

占用更多内存。3个方向的旋转需要9个数字（\(3\times3\)矩阵而言）。矩阵一多就可想而知。
人类难以使用。对于旋转，人们还是习惯用角度来思考，即便你十分了解矩阵，也不如直接看欧拉角来得直观。
矩阵可能格式不正确。并不是随便9个数都能构造出旋转矩阵，也就是说矩阵格式是可能出错的。比如在进行大量矩阵乘法后，由于浮点舍入误差的累积，可能让数据出错导致矩阵格式错误。这种现象叫矩阵蠕变，但可以用正交化来抵消。

3.欧拉角

1.欧拉角介绍

欧拉角将定向描述为围绕3个垂直轴对的3个旋转。我们使用最常见的约定（也就是说这不是唯一定义欧拉角旋转的方法），即“航向-俯仰-滚转”约定，也就是我们曾经学过的，最熟悉的约定。我们可以简单的通过四步，将一个欧拉角要描述的方向确定下来：

无论如何标记轴，第一个角度需要绕竖直轴旋转；第二个角度围绕体横向轴旋转；第三个角度围绕体纵向轴旋转。这就像是一个从直立坐标变换到对象坐标的过程。
欧拉角围绕体轴旋转，也就是说下次旋转的轴向会随先前的旋转而变化；在固定轴系统（直立空间）中，轴始终是不变的。而比较反直觉的是，只要让固定轴用相反的顺序进行旋转，二者就是等效的。例如，将某对象绕\(y\)轴旋转了\(h\)，又绕对象空间的\(x\)轴旋转了\(p\)，这和先绕直立空间的\(x\)轴旋转\(p\)，再绕直立空间的\(y\)轴旋转了\(h\)的结果是一样的（你可以试试看）。原因我们后面说。

2.欧拉角的优点

易与人类使用，欧拉角的3个数全是角度，很符合人类自然的思考方式。
最小的表示定向的方法。没有少于3个数设置三维定向的方法，所以欧拉角表示定向是最经济的方式。而且，欧拉角直接记录角度，不需要三角函数，存储更准确。
任意3个数字都可以组成有效的欧拉角。

3.欧拉角的缺点

给定定向的表示不是唯一的。这点很容易想到，因为我们在学习极坐标时，就有了解过别名现象。在实际使用欧拉角时也有一些规范条件：

别名也不会影响实际定向吧，有必要进行规范吗？单论指定方向，那确实不需要，但如果我们需要对两个定向之间进行插值计算呢？比如，我想平滑地将相机从一个方向转到另一个方向从而达成一个运镜效果，这时如果不用规范的欧拉角的话，即便只是让相机“抬个头”，也可能会转出一个非常离谱的角度。

但仅仅规范角度，那也还会遗留一个小问题：绕远路。

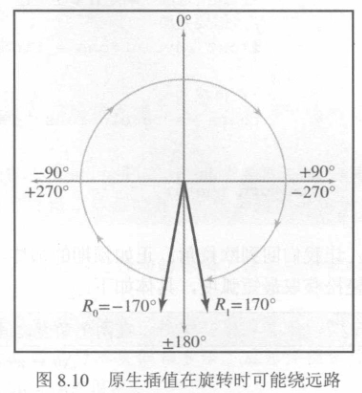
如果确实需要找到最短的弧，那解决方法就是：将角度限制在\(\pm 180^\circ\)之间。
事情完美解决了吗？你可能注意到了，最后一条规范条件看起来很奇怪，其实它是针对一种叫万向节死锁的情况给出的。万向节死锁，可能得通过这个视频你才能了解清楚，它是欧拉角无法解决的问题，我们也只能通过修改旋转轴的执行顺序来减小发生这种情况的可能，但无法彻底避免。

4.轴-角和指数映射表示方式

以欧拉冠名的东西里还有一个叫欧拉旋转定理，其基本意思是说，总可以挑出一个轴，让一个定向绕它旋转一次就变换到想要的另一个定向。这个定理导致了两种密切相关的描述定向的方法。

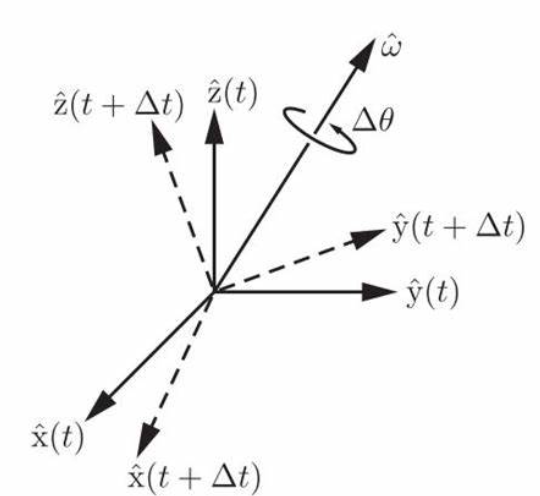
假设我们选择了旋转角\(\theta\)和穿过原点的旋转轴并且平行于单位矢量\(\hat{n}\)，这就是轴-角形式的角位移。由于\(\hat{n}\)具有单位长度，我们可以将其乘上\(\theta\)而不会丢失信息，并得到\(\vec{e}=\theta\hat{n}\)，这就是另一种描述旋转的方案指数映射（这个名词其实有更深层的意思，本书作者为了找合适的描述术语，将它的原意淡化了）。

单从 \(\vec{e}\) 就能得到旋转变换？是的，因为\(\theta=\begin{Vmatrix}e\end{Vmatrix}\)，所以通过它的长度我们可以知道要旋转的角度，我们将 \(\vec{e}\) 归一化就又获得了轴 \(\hat{n}\)，它的表达比轴-角更紧凑，而且更方便进行计算（比如插值）。甚至连轴-角的特殊能力：可以将 \(\theta\) 乘上一个数 \(k\)，来表示旋转的 \(k\) 倍的旋转。指数映射也能用同样的方式做到。

总之，指数映射比轴-角更常用，它最重要和最频繁的用途是存储角位移；在描述旋转率时，还可以通过简单的矢量加法来连接多个旋转（这个得在往后的章节再进一步解释了）。但指数映射和轴-角也同样存在别名现象和奇点现象（万向节死锁）。奇点现象其实很容易想到，当 \(\theta=0\) 时就是，因为这种情况选什么轴都可以，但好在这种奇点现象对实际的负面影响不大。

别名有两种：一种是将 \(\theta\) 和 \(\hat{n}\) 都取负，这样就得到了一种别名，不过指数映射避开了这个问题，因为这种情况下求得的\(\vec{e}\)与原本一样；另一种就和欧拉角一样了，还是角度的范围问题，我们也可以通过给出规范限制来解决，然而，这种情况并非完全不好。假如我们有意区分旋转\(360^\circ\)和旋转\(720^\circ\)，那我们就可以利用这种别名（四元数做不到）。
事实证明，我们可以将任何旋转矩阵描述的角位移都转成唯一确定的指数映射，更是可以用指数映射子集与旋转矩阵形成一对一的对应关系。这是欧拉旋转定理的本质。

5.四元数

四元数几乎和欧拉角同样出名，我们也因为对它的陌生和表象的复杂而感觉“难以理解”，但这次我们希望能消除这种“神秘感”~~（本书作者说的~~。

1. 四元数的表示

四元数由一个标量和一个三维矢量组成：

与常规矢量不同，四元数的“行”和“列”形式没有区别，可以出于美观考量自由选择形式。这种形式多少让人想起前面轴-角和指数映射形式，四元数的确也是由与轴和角度相关的数组成的：

这种书写方式是旋转四元数，这种形式的四元数是我们重点关注的。但它看起来十分奇怪，这是因为四元数它是 「借助」四维的神秘力量来进行三维旋转的。这并不是玩笑，而且我们也不是第一次接触这种情况，我们曾在 \(4\times4\) 矩阵中用过类似的说法。四元数的起源故事告诉我们，它是三维的复数（虚数），从几何意义上来讲，它确实以三维的形式让我们得以窥见四维的一隅。由于篇幅所限，我们不会再详细探讨它的几何解释，但是！有大佬通过视频将它更直观的体现了出来，一定要看啊！

2.四元数的数学（纯记录）

四元数变负
四元数可以变负，让每个分量都变负就可以了：

四元数变负后描述的角位移和之前是一样的（相当于原本的 \(\theta\) 加上\(360^\circ\)）。
单位四元数
在几何学中，由两个单位四元数代表“没有角度位移”：

这里的0是零矢量\(\vec{0}\)。单位四元数的值就是来源于\(\theta\)是\(360^\circ\)的偶数/奇数倍时的取值。我们可以这么理解：如果旋转角度\(\theta\)是围绕任何轴旋转完整的圈数，则在方向上没有任何改变。
但从代数上来说，只有一个单位四元数：\([1,0]\)。
四元数的大小
四元数的大小计算和矢量类似：

对于我们为了表示定向而使用的旋转四元数，它都有单位大小：
四元数的共轭和逆
四元数的共轭用\(q*\)表示，将矢量部分变负即可：

四元数的逆用\(q^{-1}\)表示，用四元数的共轭除以其大小得到：

对于旋转四元数而言，共轭和逆是相等的，我们可以用它表示相反的角位移。可以理解成将旋转轴不变，但旋转角度变负，从而颠倒了原本旋转的方向。
四元数乘法
四元数的乘法从右向左读取，它是根据复数的定义推导出来的（包括随后的几个性质）：

它的乘法具有以下属性：
a. 可结合但不可：\((ab)c=a(bc)\)
b. 乘积的大小等于大小的乘积：\(\begin{Vmatrix}q_1q_2\end{Vmatrix} = \begin{Vmatrix}q_1\end{Vmatrix}\begin{Vmatrix}q_2\end{Vmatrix}\)
c. 乘积的倒数等于反顺序取倒数的乘积：\((ab)^{-1}=b^{-1}a^{-1}\)

是否觉得很熟悉？它和矩阵之间的关系或许真的比较密切（后面会提到）。四元数也可以用乘法来表示应用了旋转变换，设一个四元数\(p=[0,(x,y,z)]\)，它将一个三维点\((x,y,z)\)“扩展”到四元数空间；再设\(q\)是\([\cos\frac{\theta}{2},\hat{n}\sin{\frac{\theta}{2}}\)]形式的旋转四元数，那么将\(p\)应用\(q\)旋转则为：

请你先接受这一点，四元数乘法也可以像矩阵一样（其实有小小的差别）连接多个旋转：

四元数的“差”
这里的“差”并不是指两个四元数大小相减，而是两个四元数所代表的定向之差，也就是相差的角位移。例如，要求从\(a\)到\(b\)旋转的角位移\(d\)，就可以这么求：

简直像是除法（对比于：\(da=b\)），你可以这么认为，但要记住四元数并没有除法。
四元数点积
四元数点积就更熟悉了，和矢量几乎一样：

它也有和矢量点积类似的解释：\(a·b\)的绝对值越大，它们的角位移就越“相似”。
同样和矢量一样的还有，与标量的乘法：
四元数的对数函数、指数函数
上述3个运算很少直接使用，但它们是几个重要四元数运算的基础。
首先，我们用半角\(\alpha\)从新定义下四元数：

四元数的对数的定义如下：

我们用\(\equiv\)表示相等的定义，也可以注意到最终得到的格式和指数映射挺像的。
反过来，我们也可以得到四元数的指数函数：
四元数的指数运算
注意，接下来的「四元数的指数」指指数运算（\(q^t\)），而不是之前的指数函数。通过指数，可以提取角位移的“分数”。比如要计算四元数\(q\)表示的位移的三分之一，就可以用\(q^{\frac{1}{3}}\)求得。负指数表示反向旋转的倍数。
但需要注意：四元数表示的角位移都是最短弧，也就是说如果\(q=30^\circ\)，那\(q^8\)表示的不是顺时针的\(240^\circ\)，而是逆时针的\(120^\circ\)。
利用之前得到的四元数指数函数，我们可以求得四元数的取幂公式：
四元数的插值
四元数有一种称为 「Slerp」 的独特插值运算，代表的是球面线性插值。它能完美解决欧拉角插值的所有问题。根据之前所学，我们知道四元数的运算比较特殊，所以要进行插值的话，我们要将插值公式“翻译”一下。
原本的插值公式（小改了下顺序以便与四元数进行对照，毕竟四元数的乘法顺序不能乱改）：
\(lerp(a_0,a_1,t)=t(a_1-a_0)+a_0\)
用\(q_0\)表示四元数形式的\(a_0\)，同样，\(q_1\)表示\(a_1\)，我们就可以得到：
\(slerp(q_0,q_1,t)=(q_1q_0^{-1})^tq_0\)
从数学上来说，已经结束了。但在实践中，我们会用等效的简化过的替代公式：

它的推导过程如下（要写字的话太多啦）：

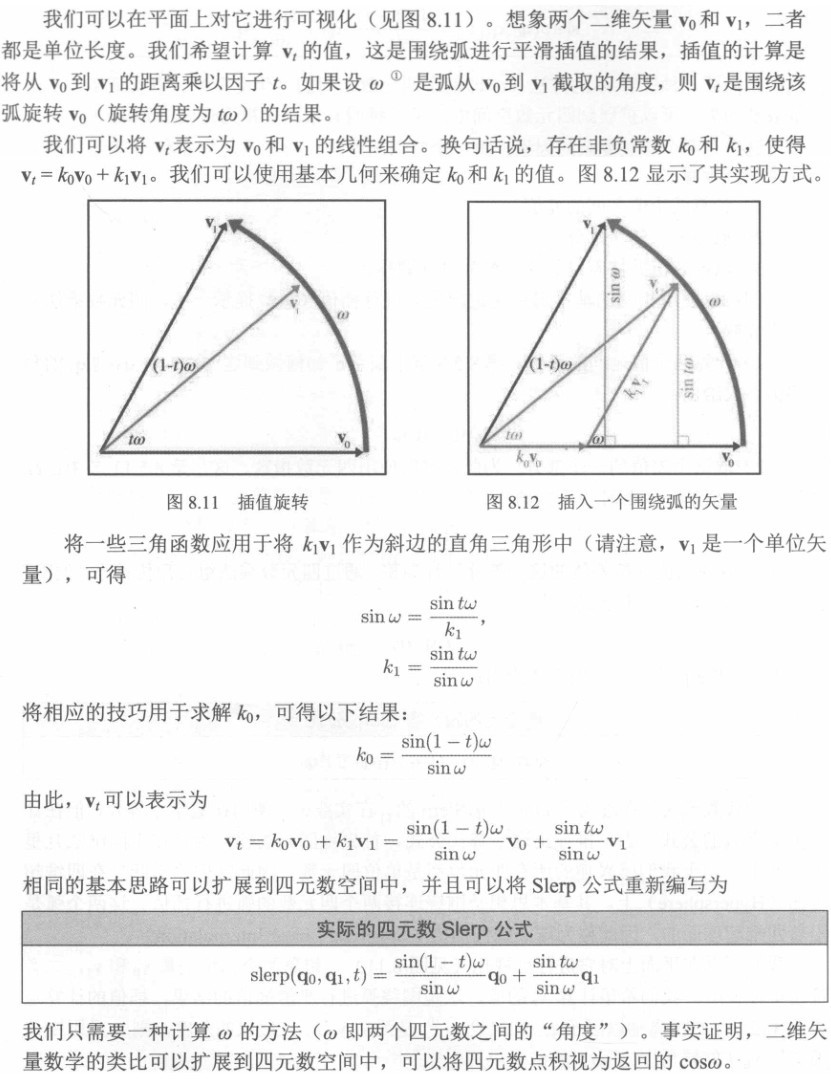
3.四元数的优点

绝无仅有的平滑插值。
角位移的快速连接和逆向，这两点与矩阵旗鼓相当。
可以快速转换成矩阵（后面会提到）。
只用了4个数字。比矩阵少5个，比欧拉角多1个，还是很不错的。

4.四元数的缺点

比欧拉角大一点。虽说只多1个，但欧拉角总共就3个，~~（四舍五入~~相当于多了三分之一的内存。
可能无效。和矩阵类似，并非随便套4个数都能组成有效的四元数，所以也要考虑累积浮点误差。但好在也和矩阵类似，可以通过规范化四元数确保它具有单位大小来解决这个问题。
人类难以直接使用（这点不必多少吧）。

6.方法比较

回顾下前面描述的几种方法之间的差异：

作者也有给出一些选择建议：

欧拉角最容易使用，不要以“优化”的名义牺牲易用性。
如果需要矢量坐标空间转换，可以用其它形式储存方向，但最终必须使用矩阵形式。
要存储大量方向（如动画数据），可以考虑欧拉角、指数映射和四元数。
需要可靠的插值就用四元数，也可以将别的形式转换为四元数。
需要“额外旋转”的情况，可以使用指数映射或轴-角。

7.表示方式之间的转换

我们已经大概清楚了各种旋转的表示以及它们的特长，根据实际情况，在适当时机转换表示方式就可以扬长避短。

欧拉角转换为矩阵
转换到矩阵会有两种结果，一种是「从对象空间到直立空间的矩阵」，一种是「直立空间到对象空间的矩阵」：

而要求后者，其实就是求前者的转置：
矩阵转换为欧拉角
考虑到欧拉角的规范条件，可能会繁琐些。首先我们将矩阵按照1中的结论，以那种形式扩展：

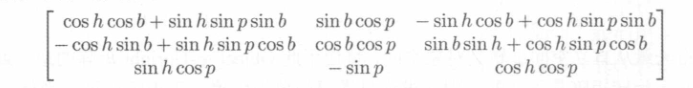
我们用 \(m_{ij}\) 表示\(i行j列\)的元素。
\(p=asin(-m_{32})\)，
其中的asin函数来自C标准库函数，是返回\([-90^\circ, 90^\circ]\)的 \(\arcsin\)。
\(h=atan2(\frac{m_{31}}{\cos{p}}, \frac{m_{33}}{\cos{p}})=atan2(m_{31}, m_{33})\)，
\(atan2\)函数我们之前介绍过了，它通过\(\frac{y}{x}\)获得\(\tan\)值，然后再计算出反正切，因此可以再简化为最后的式子（商不会变）。
\(b=atan2(m_{12},m_{22})\)，同上简化了算式。
但这样的计算就得考虑\(\cos{p}=0\)（其实就是万向节死锁）的特殊情况了，所以我们在计算前要对它单独处理：
四元数转换为矩阵
这个推导有点复杂，我就跳过了（抱歉
矩阵转换为四元数
同样用到3中的结果，进行逆向，我们可以得到：
\(w=\frac{\sqrt{m_{12}+m_{22}+m_{33}+1}}{2}\)
\(x=\frac{\sqrt{m_{11}-m_{22}-m_{33}+1}}{2}\)
\(y=\frac{\sqrt{-m_{11}+m_{22}-m_{33}+1}}{2}\)
\(z=\frac{\sqrt{-m_{11}-m_{22}+m_{33}+1}}{2}\)
计算过程看起来不会太难，但结果该选择正根还是负根？因此，我们只能选择这4个中的一个作为基础判断，并推导出另外3个。

那该选哪个呢？我们可以根据\(w、x、y和z\)中谁的绝对值最大来决定。
欧拉角转换为四元数
和转换为矩阵一样，我们也可以将欧拉角转换为「从对象空间到直立空间的四元数」和「从直立空间到对象空间的四元数」这两种情况。我们也可以仿照转换为矩阵的过程：

而求后者，也像矩阵那样，求前者的“转置”，在四元数中就是共轭：
四元数转换为欧拉角
将四元数转换为欧拉角同样要考虑到它的规范，这样的事我们在矩阵转为欧拉角时就已经做过了。所以我们可以先把四元数转换为矩阵，再把矩阵转换为欧拉角，最后化简中间的环节。
最终结论如下：