第六章:矩阵详解
第六章:矩阵详解
本章将通过讨论一些有用的矩阵运算来结束矩阵主题。(终于
1.矩阵的行列式
行列式是方形矩阵特有的一个特殊标量。我们会先讨论数学,再做一些几何解释。
1. 行列式的运算
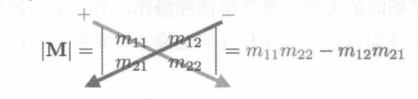
一个矩阵 \(M\) 的行列式用 \(|M|\) 表示。行列式的计算或许看起来会很奇怪,来看看 \(2\times2\) 矩阵的行列式:

我们可以这么记它的计算过程:
再来看看 \(3\times3\) 矩阵的:

额,似乎开始复杂了,不过我们还有一种好记的方法:
我们可以复制一份矩阵拼在后面,然后按下图的方式计算

而这里有个特殊情况,如果这个 \(3\times3\) 解释为3个行矢量的话,那么这个矩阵的行列式等价于这三个矢量的三重积:

在看一般矩阵的行列式前,我们还要了解两个东西:子矩阵行列式和余子式。
子矩阵,就是将一个矩阵删掉一行和一列后剩下的矩阵,比如,将矩阵 \(M\) 删掉第1行和第2列:

我们用 \(M^{\{ij\}}\) 表示一个矩阵删除了第i行和第j列后的子矩阵。子矩阵行列式就是子矩阵的行列式。想必你也猜到了,一个矩阵大多都会有不止一个子矩阵。
余子式,就是在子矩阵的基础上做了个小小的符号变换:

虽说本身不复杂,但配合下面这张图可以让你记得更牢些:

现在可以看看一般情况下的矩阵如何计算行列式了,对于任意维数 \(n\times n\)的矩阵,我们首先选择它的任意一行(或一列),再将该行(或列)的每个元素乘上它的对应余子式,将这些乘积求和,就可以得出行列式:

 ̄へ ̄,你是否明白了?再给你个 \(3\times3\) 的对照上面的内容看看:

你也可以试试求 \(4\times4\) 矩阵的行列式,它的计算应该是这样的:
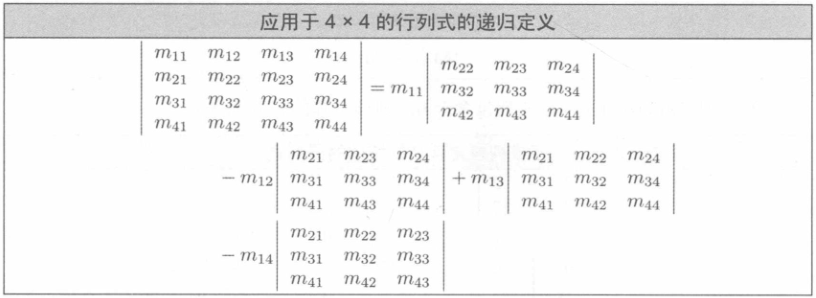
如果我们再套个娃,把上图中的3维子矩阵也用这样的方法求行列式,那就会得到:

那 \(5\times5\) ……够了!( ̄ε(# ̄)☆╰╮o( ̄皿 ̄///)已经足够了!对于这本书而言,我们所能接触的最大矩阵就是 \(4\times4\) ,不需要更大的矩阵了。不过善良的你也不需要为那些需要计算更大矩阵的人感到同情,还有些特殊的技巧可以化简计算。不过我们用的这些矩阵都算是简单的,根本用不着,也就不介绍了。
最后我们来看一些行列式有关的重要特征:
- 单位矩阵的行列式为1;
- 矩阵乘积的行列式等于行列式的乘积;
- 矩阵转置的行列式等于原始矩阵的行列式;
- 如果矩阵有一行(列)为全0,那行列式就为0;
- 交换任意两行(列)的位置,行列式会变负;
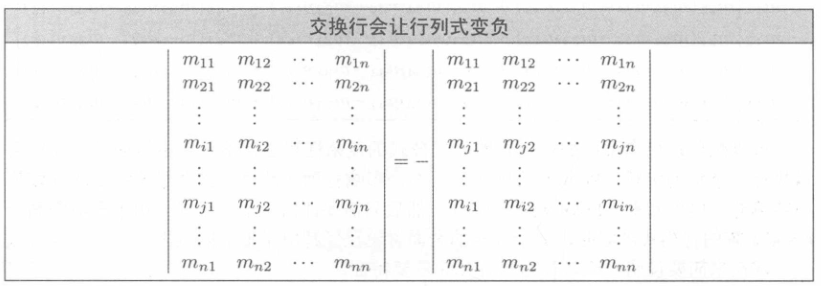
- 将行(列)的乘上任意倍数加给另一行(列),行列式的值不变。(因此,错切矩阵的行列式为1)

2. 行列式的几何解释
到目前为止,我们似乎接触了很多概念,但仔细一想,它们都是为了计算行列式而搞出来的。那行列式究竟是什么?它的计算为什么这么奇怪?
我先给出结论:行列式就是矩阵的变换程度。
这有令你感到惊讶吗?回顾一下,我们学了这么久矩阵也确实还没有提到过矩阵的“大小”。在第四章时我们得出了一个结论:矩阵就是变换,而它能表达的变换多种多样,我们该如何比较哪种变换更“剧烈”呢?将矩阵当成基矢量组画在坐标上可以吗?当然是可以的,但未免麻烦了些、主观了些,我们能否像计算矢量大小那样,从组成矩阵的这几个数字里找到这样一种衡量变换大小的规律呢?
人们也找到了,就是行列式。它的计算虽说奇怪,但如果我们将它画出来,你会发现合情合理。就以简单的二维矩阵为例,在二维中,矩阵的行列式就是变换后的基矢量形成的平行四边形的面积(下图黄色区域)。我们可视化一下它:
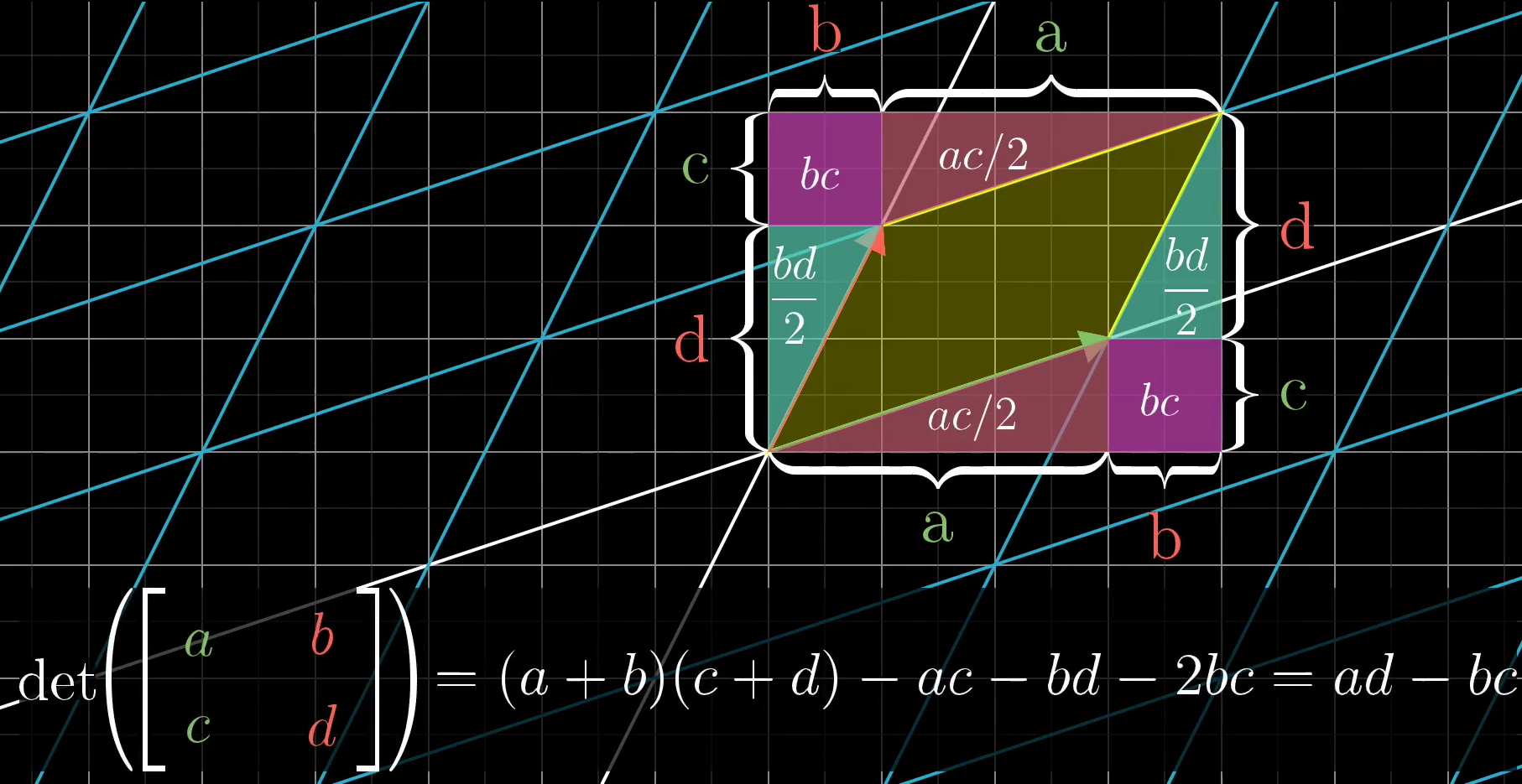
而在三维中,矩阵的行列式就是变换后的基矢量形成的平行六面体的体积。

更高维的我们无法想象出来,但我们可以猜到,那维数的矩阵行列式一定是在衡量属于那一维度的变化。而且也能用那种近似层次分解、变成多个低维矩阵的计算方式求得其变化程度,即便我们无法想象。
但还有个小小的问题,行列式的值有时是0,甚至是负数,这怎么解释?
是的,刚刚说的那些,更多是指矩阵行列式的绝对值代表的变换,都是发生在本身坐标空间下的变换。而行列式的符号则代表矩阵所在坐标空间的变换。希望没把你绕晕,我直说可能会更好些:
1. 如果行列式为0,表示发生了“降维”,也就是投影(从体变成了面或从面变成了线)
2. 如果行列式为负数,表示发生了“翻转”,也就是反射。
2. 逆矩阵
除了行列式,还有一个独属于方形矩阵的运算,叫做逆矩阵,简称逆。接下来同样先数学后几何。
1.逆矩阵的运算
一个方形矩阵 \(M\) 的逆矩阵,表示为 \(M^{-1}\) 当一个矩阵乘上它的逆矩阵后会得到单位矩阵。

但并非所有矩阵都有逆矩阵,比如有个矩阵它的某行(列)都是0,那它无论怎么乘都得不到单位矩阵。像这种没有逆的矩阵就叫不可逆矩阵,什么?名字太普通了?那它还可以叫奇异矩阵;有逆的矩阵,就叫可逆矩阵,或者非奇异矩阵。我们也可以得出:奇异矩阵的行列式一定是0,非奇异矩阵的行列式一定不是0。
我们计算矩阵的逆矩阵的方法是经典伴随方法,所以先来看看什么是经典伴随矩阵。(这意味着其实还有别的计算方法,那些方法更适用于较大的矩阵,我们用不着。而且经典伴随方法不需要任何if的判断或其它分支,对今天的超标量计算体系结构和专用矢量处理器来说更快捷。)
矩阵 \(M\) 的经典伴随矩阵表示为"\(adj M\)",被定义为 \(M\) 的余子式的矩阵的转置。比如有个矩阵 \(M = \begin{bmatrix}
-4&-3&3\\
0&2&-2\\
1&4&-1\
\end{bmatrix}\),它的经典伴随矩阵就要这么算(各个余子式的计算过程就省略啦):

有了经典伴随矩阵,逆矩阵的计算就简单了:

来看看矩阵求逆的一些重要特性:
- 矩阵的逆矩阵的逆矩阵是它本身:\((M^{-1})^{-1}=M\)
- 单位矩阵的逆是它自己:\(I^{-1}=I\)
- 矩阵转置的逆是矩阵逆的转置:\((M^T)^{-1}=(M^{-1})^T\)
- 矩阵乘积的逆等于矩阵的逆的相反顺序的乘积:\((AB)^{-1}=B^{-1}A^{-1}\)
- 逆矩阵的行列式是原始矩阵的行列式的倒数:\(|M^{-1}|=\frac{1}{|M^{-1}|}\)
2. 逆矩阵的几何解释
这次的几何解释很直白:一个矩阵的逆矩阵,能“撤销”该矩阵变换的矩阵。也就是说它代表的是抵消变换、恢复成原始形态。带着这种想法,我们就能明白为什么有些矩阵没有逆矩阵,因为经过这些矩阵变换后,无法恢复了!有什么变换会这样呢?其实所有“降维”的变换都是,所以再看看开始就提到的“某行(列)都是0”的矩阵,不就是在某个轴向上被压缩成0的“降维”变换吗。明白了这点后,再看看之前提到的“重要特性”,你应该就能更清楚它们的几何含义了。
3.正交矩阵
如果一个方形矩阵与它的转置的乘积是单位矩阵时,我们就说这个矩阵是正交的,也叫它为正交矩阵。

感觉有点眼熟……哦~是刚刚提到的逆矩阵的定义:\(MM^{-1}=I\)
。这么说来,对正交矩阵而言,转置矩阵和逆矩阵是相等的。这一点非常关键,毕竟求一个矩阵的转置比求一个矩阵的逆要简单得太多太多了(想起来《线性代数》作业的繁琐计算
。
要使矩阵正交,必须要让矩阵的每一行(列)都是单位矢量,并且行(列)之间要相互垂直。这很直白了,它的几何解释很简单,就是由一组标准正交基构造出的矩阵。
在一些情况下,我们希望将一个矩阵正交化,但又尽可能接近原始矩阵。这时就需要一些计算了,我们要用到Gram-Schmidt正交化算法。其基本思想是按顺序遍历基矢量,对于每个基矢量,都减去与它平行的矢量,最终就会产生垂直矢量(还记得第二章提到的吗?在标准正交基矢量下,任何矢量都可分解成垂直和平行两个部分:\(\vec{b}=\vec{b}_{||}+\vec{b}_{⊥}\),既然平行的都被减去了,剩下的就是垂直的了)
算法细节就不说了,这里就给出三维的、结合了偏差消除的Gram-Schmidt算法:

4.关于 \(4\times4\) 齐次矩阵
四维矢量在三维的x、y、z的后面再加了个w,四维矢量也被称为齐次坐标。而之所以我们要引入四维的矩阵和矩阵并不是为了研究四维空间,而是为了简化三维运算(就像往期提到过的,将三维矩阵升维就可以在矩阵中表示平移)。
既然是为了简化三维运算,那四维和三维的关系是什么?这可真让人摸不着头脑,毕竟这样的空间无从想象(不要把这里的第四维解读成“时间”啊)。但我们可以通过把二维扩展成三维的例子来理解如何把三维扩展到四维。
二维中的齐次坐标形式为\((x,y,w)\),现在有个二维平面在三维中的\(w=1\)的位置,我们可以把三维中的点投影到这个平面上。
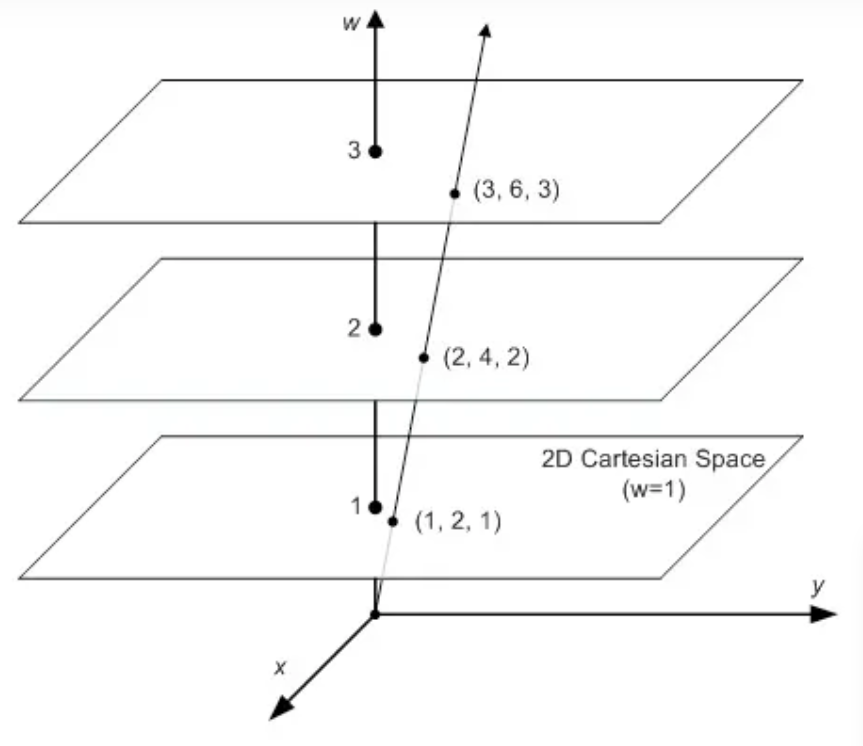
(+_+)?欸?这是什么投影方式?其实就是把\((x,y,w)\)都除以w,得到\((\frac{x}{w},\frac{y}{w},1)\)。
那不用能减法把点变成\(w=1\)吗?当然不可以,用了减法就会改变坐标间点的相对位置关系,这样就不叫投影了,反观通过除法,我们只要通过 \(w\) 就能一窥它在三维的位置。而且,减法无法表示沿某方向“无穷远的点”,但除法可以,如果你学过高等数学中的「极限」,你应该可以理解这一点——\((x,y,0)\),这种形式的点就表示它在二维中的“无穷远的点”。如果你没学过也没关系,你就理解成当\(w=0\)时,我们之前给出的那种除法是未定义的,就用它当“无穷远的点”。这种情况下,“无穷远的点”不再被当成一个位置,而是定义方向。
同样的逻辑,我们放到三维中,一个三维点\((x,y,z)\)可以理解为是在一个四维的\(w=1\)的超平面上,也就是说,它也是通过\((\frac{x}{w},\frac{y}{w},\frac{z}{w},1)\)投影来的。\((x,y,z,0)\)也用来定义方向。
那我们试试把 \(3\times3\) 变换矩阵扩展到四维:

这种扩展是合理的,可以看到进行矩阵乘法时除了四维的\(w=1\)之外,其它都还是不变(这再好不过,毕竟我们也只关注三维):

那这个四维矩阵该如何表示三维的平移呢?答案是错切。

你是否还记得错切变换矩阵呢?回顾下三维的\(xy\)错切矩阵:\(H_{xy}(\Delta{x},\Delta{y})=\begin{bmatrix}
1&0&0\\
0&1&0\\
\Delta{x} &\Delta{y}&1\\
\end{bmatrix}\),是一样的形式,也就是说高维的错切可以表示低维的平移。
如果你还不明白,那可以看看三维错切的样子:
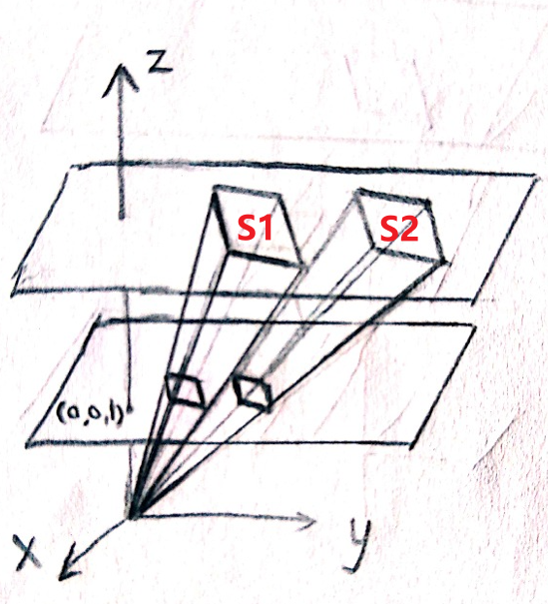
锥体\(S_1\)经过错切变换到\(S_2\),但在\(w=1\)的二维平面中投影的面积形状并没有变(我画的有些不准,但请你相信这点),根据错切的特点(忘了的话记得看第五章),这理所当然。但我们发现它投影的位置发生了移动!这不就是二维的平移吗?既然二维的平移可以是三维的错切,我们也可以相信(计算可以证明也确实如此)在三维空间的移动也可以是四维空间的错切。
最后,我们来看看那个“无穷远的点”在四维中会怎么样吧:

可以看到,它只是变成了另一种形式的“无穷远的点”而已。那它能平移吗?

它的坐标位置并没有变化,所以显然不行,我想这应该不用过多解释。
最后让我们看看 \(4\times4\) 齐次坐标的另一个妙用:透视!
笛卡尔空间下的投影产生的图像并不能表示那种“近大远小”的透视感:

但使用齐次坐标的投影方式就可以做到:

这种投影我们称为透视投影,它也可以表达成变换矩阵,以投影到\(z=d\)的平面为例,只需要将矩阵乘上\(\begin{bmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&1&\frac{1}{d}\\
0&0&0&0
\end{bmatrix}\)就可以了。为什么三维投影到二维也要用 \(4\times4\) 矩阵?当然是为了更其它变换矩阵统一,所有矩阵都用这种形式就可以互相乘,方便执行复合变换。投影到其它主平面的矩阵你应该也能猜到,这些的推导就省略啦。

