求组合数(模板)【组合数学】
数学公式
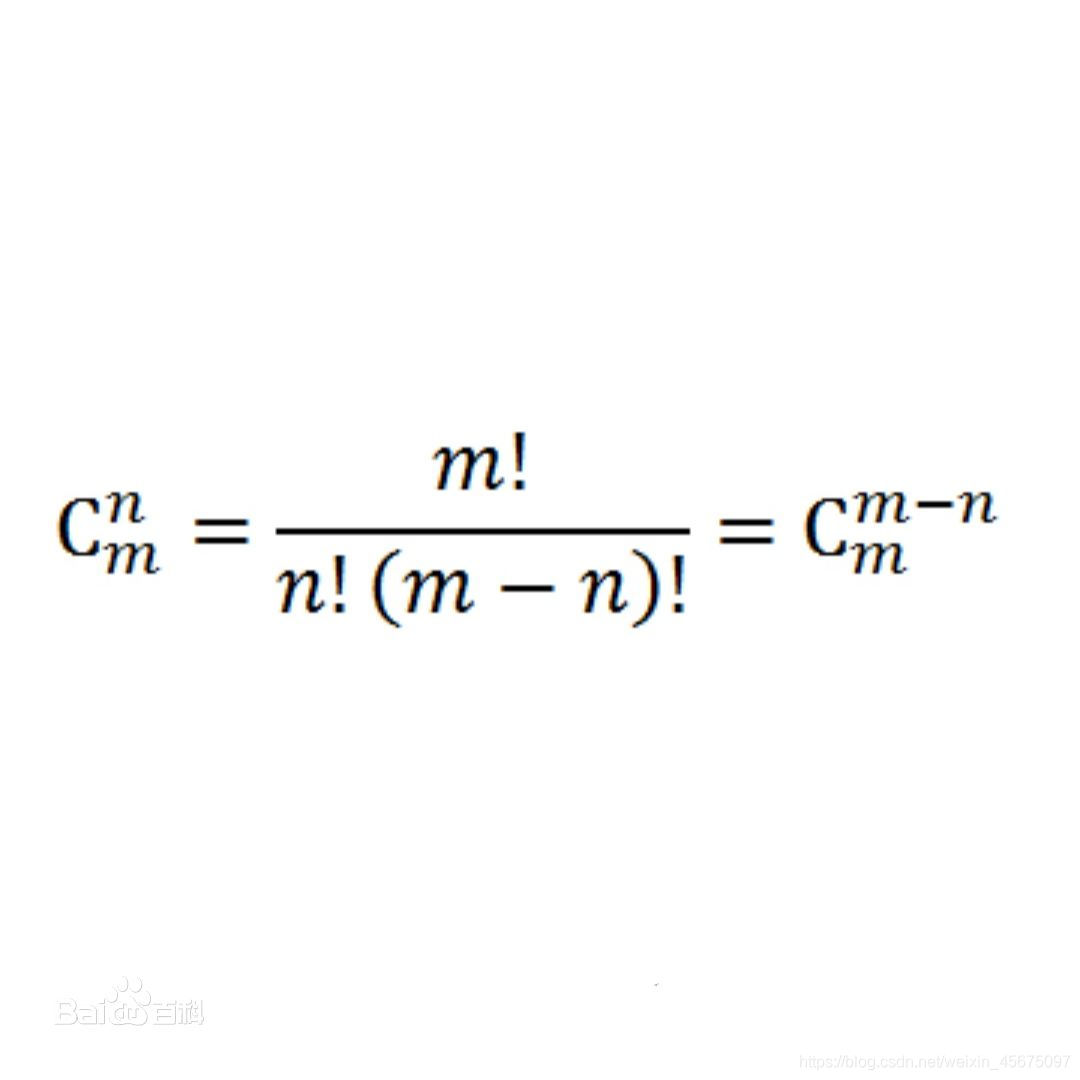
一.递推
组合数有一个重要的性质:C(n,m)=C(n,n-m)=C(n-1,m-1)+C(n-1,m)。
该公式的证明也很好想,比如我们定义C(n,m)是从n个苹果里选择m个苹果,那么我们对于第n个苹果,我们有选和不选两种选择;如果我们选择第n个苹果,就只需要在剩下的n-1个苹果中选m-1个;反之,如果我们不选第n个苹果,就需要在剩下n-个苹果里选m个苹果。其实该公式与杨辉三角也有着密切的联系,具体证明可参考大佬博客。
原题链接:885. 求组合数 I
#include<bits/stdc++.h>
using namespace std;
const int N = 2100;
const int mod = 1e9+7;
int c[N][N];
void init(){
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++){
if(j==0) c[i][j]=1;
else c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
}
}
int main(){
init();
int n;
int a,b;
cin>>n;
while(n--){
cin>>a>>b;
cout<<c[a][b]<<endl;
}
return 0;
}
二.预处理阶乘+逆元
886. 求组合数 II
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
const int mod = 1e9+7;
ll fact[N];//阶乘
ll infact[N];//逆元
ll ksm(ll a,ll b,ll p){
ll res=1;
while(b){
//&运算当相应位上的数都是1时,该位取1,否则该为0。
if(b&1)
res=1ll*res*a%p;//转换为ll型
a=1ll*a*a%p;
b>>=1;//十进制下每除10整数位就退一位
}
return res;
}
void init(){
fact[0]=1;
infact[0]=1;
for(int i=1;i<N;i++){
fact[i]=fact[i-1]*i%mod;
infact[i]=infact[i-1]*ksm(i,mod-2,mod)%mod;
}
}
int main(){
init();
int n;
cin>>n;
int a,b;
while(n--){
cin>>a>>b;
cout<<fact[a]%mod*infact[b]%mod*infact[a-b]%mod<<endl;
}
return 0;
}
ll c(ll a,ll b,ll p){
if(b>a) return 0;
ll res=1;
for(int i=1,j=a;i<=b;i++,j--){
res=res*j%p;
res=res*ksm(i,p-2,p)%p;//逆元
}
return res;
}
三.lucas定理 p为质数
C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ksm(ll a,ll b,ll p){
ll res=1;
while(b){
//&运算当相应位上的数都是1时,该位取1,否则该为0。
if(b&1)
res=1ll*res*a%p;//转换为ll型
a=1ll*a*a%p;
b>>=1;//十进制下每除10整数位就退一位
}
return res;
}
ll c(ll a,ll b,ll p){
if(b>a) return 0;
ll res=1;
for(int i=1,j=a;i<=b;i++,j--){
res=res*j%p;
res=res*ksm(i,p-2,p)%p;//逆元
}
return res;
}
ll lucas(ll a,ll b,ll p){
if(a<p &&b<p) return c(a,b,p);
return c(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main(){
int n;
ll a,b,p;
cin>>n;
while(n--){
cin>>a>>b>>p;
cout<<lucas(a,b,p)<<endl;
}
return 0;
}
四.扩展lucas定理 p为合数
大佬博客
五.分解质因数+高精度乘法
(待补)
题目
1.瞬间移动
原题链接
大意:从左上角走方格,每一次只能向右下走,问走到第m行第n列的方案数。
暴力打表找规律0.0
不难看出c(n,m)=c(n-1,m)+c(n,m-1)
然后盲猜emm
还是看下大佬的证明吧
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ksm(ll a,ll b,ll p){
ll res=1;
while(b){
//&运算当相应位上的数都是1时,该位取1,否则该为0。
if(b&1)
res=1ll*res*a%p;//转换为ll型
a=1ll*a*a%p;
b>>=1;//十进制下每除10整数位就退一位
}
return res;
}
ll c(ll a,ll b,ll p){
if(b>a) return 0;
ll res=1;
for(int i=1,j=a;i<=b;i++,j--){
res=res*j%p;
res=res*ksm(i,p-2,p)%p;//逆元
}
return res;
}
ll lucas(ll a,ll b,ll p){
if(a<p &&b<p) return c(a,b,p);
return c(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main(){
ll a,b,p;
p=1000000007;
while(~scanf("%lld%lld",&a,&b)){
cout<<lucas(a+b-4,b-2,p)<<endl;
}
return 0;
}
其他题目待补


