UPC-篮球运动（线性DP）

篮球运动

时间限制: 1 Sec 内存限制: 128 MB
[提交] [状态]
题目描述
小明建造了一个篮球场，他请来了2行n列的人，想让他们进行比赛。每一个人都有一个能力值，第一行分别为h11，h12，…，h1n，第二行为h21，h22，…，h2n。现在小明可以选一些人组成一个最强团队。但是选人是有规则的，因为选一个人会让附近的人都很妒忌，所以他既不会同一行里连续选择2个人，也不会同一列里的连续选择2个人。
现在他希望所选团队的能力值的之和最大，但人太多了，所以他想请聪明的你帮他解决这个问题。解决在满足规则的情况下能力值的和最大为多少？

输入
第一行输入一个整数n（1≤n≤105），表示每行中的学生人数。
第二行输入n个整数h[1,1]，h[1,2]，…，h[1，n]（1≤h[1，i]≤109），其中h[1，i]表示第一行中的第i个学生能力值。
第三行输入n个整数h[2,1]，h[2,2]，…，h[2，n]（1≤h[2，i]≤109），其中h[2，i]表示第二行中的第i个学生能力值。
输出
输出一个整数，表示所选团队中能力值之和最大。
样例输入 Copy
【样例1】
5
9 3 5 7 3
5 8 1 4 5
【样例2】
3
1 2 9
10 1 1
【样例3】
1
7
4
样例输出 Copy
【样例1】
29
【样例2】
19
【样例3】
7
提示
样例1说明：小明可以选择以下团队：9，8，7，5.
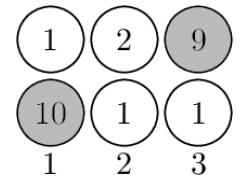
样例2说明：小明可以选择以下团队

思路：
想到了dp但是比赛时用一维推了好久没推出来
中午看到大佬博客又想起了光光说过“dp推不出来可以先增加维数”
所以还是很好推的

dp[i][j]表示只从前i个中选且该列的状态为j的最大值
j=0表示前一列中哪个都不选
j=1表示前一列中选第一行的，这一列只能选第二行的
j=2表示前一列中选第二行的，这一列只能选第一行的

状态转移方程如下：

		dp[i][0]=max(dp[i-1][1],dp[i-1][2]);
        dp[i][1]=max(dp[i-1][2],dp[i-1][0])+a[1][i];
        dp[i][2]=max(dp[i-1][0],dp[i-1][1])+a[2][i];

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline void read(ll &x){
   ll s = 0, w = 1; char ch = getchar();
   while(ch < '0' || ch > '9'){ if(ch == '-') w = -1; ch = getchar(); }
   while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
   x = s*w;
}
const int maxn=1e5+150;
ll dp[maxn][3];
int n;
ll a[3][maxn];
void AC(){
    cin>>n;
    for(int i=1;i<=2;i++)
        for(int j=1;j<=n;j++)
            read(a[i][j]);
    dp[1][1]=a[1][1],dp[1][2]=a[2][1];
    for(int i=2;i<=n;i++){
        dp[i][0]=max(dp[i-1][1],dp[i-1][2]);
        dp[i][1]=max(dp[i-1][2],dp[i-1][0])+a[1][i];
        dp[i][2]=max(dp[i-1][0],dp[i-1][1])+a[2][i];
    }
    cout<<max(dp[n][0],max(dp[n][1],dp[n][2]));
}
int main(){
    AC();
    return 0;
}

ps:记得数组不要越界