2021河南省赛——L.手动计算(定积分)

传送门

思路：

参考博客

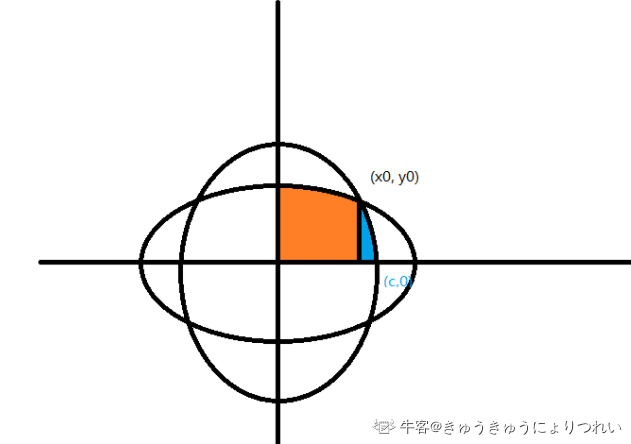
图来自参考博客
赛时想了想感觉没法将重合的部分变成规则的部分就放弃了。
可以用定积分来做，由于精度比较小，所以推出式子来写就可以。
首先，联立两个椭圆的方程算出\(x\)(也就是图中的\(x_{0}\))
其次，计算橙色部分的面积：
根据椭圆的方程我们可以知道\(y\)关于\(x\)的关系为：
\(y=\frac{b}{a}*\sqrt{a^{2}-x^{2}}\)
根据定积分橙色部分的面积为：
\(s_{1}=\int_{0}^{x}\frac{b}{a}*\sqrt{a^{2}-x^{2}} dx=\frac{b}{a}\int_{0}^{x}*\sqrt{a^{2}-x^{2}} dx\)
根据百度知道的回答
\(s_{1}=\frac{b}{a}*x*\sqrt{a^{2}-x^{2}}*\frac{1}{2}+a*b*arcsin(\frac{x}{a})*\frac{1}{2}\)

同理：蓝色部分的面积为竖向椭圆面积的\(\frac{1}{4}\)减去橙色部分减去橙色部分上方的白色部分。后者的计算跟上面\(s1\)的计算公式类似。
注意包含的情况特判一下。

代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PLL;
typedef pair<int, int>PII;
typedef pair<double, double>PDD;
#define I_int ll
inline ll read()
{
    ll x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
#define read read()
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
ll ksm(ll a, ll b, ll p)
{
    ll res = 1;
    while(b)
    {
        if(b & 1)res = res * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return res;
}
const int inf = 0x3f3f3f3f;
#define PI acos(-1)
const int maxn=1e6+10;

int main()
{
    int T=read;
    while(T--)
    {
        double a,b,c,d;
        cin>>a>>b>>c>>d;
        if(a>c&&b>d)
        {
            printf("%.1f\n",PI*a*b);
        }
        else if(c>a&&d>b)
        {
            printf("%.1f\n",PI*c*d);
        }
        else
        {
            double res=PI*a*b+PI*c*d;
            double x=sqrt(a*a*c*c*(b*b-d*d)/(b*b*c*c-a*a*d*d));
            double s1=b/a*x*sqrt(a*a-x*x)*0.5+0.5*a*b*asin(x/a);
            a=c,b=d;
            double s2=PI*c*d/4-(b/a*x*sqrt(a*a-x*x)*0.5+0.5*a*b*asin(x/a));
            res=res-s1*4-s2*4;
            printf("%.1f\n",res);
        }
    }
    return 0;
}

/*

**/