【GAMES101】学习记录4-Geometry
前言
终于来到了几何。如有错误，欢迎斧正。
记录
隐式几何
隐式几何是用抽象的数学公式或函数来记录几何，正因如此，它不够直观。
它有几种形式，如：函数表示、几何的交并差表达式、距离函数、分形等。
隐式表达的好处在于它存储方便，只需要记录对应公式或函数即可。由于它是公式或函数，所以也很方便处理光线与模型之间的运算。
显式几何
显式几何是将几何用直观的方式表现出来，如点云、多边形网格、贝塞尔曲线、贝塞尔曲面等。
点云
点云是将一堆模型上的点存储下来，用这些密集的点来组成整个模型。
毫无疑问，对于精细的模型来说，这种方式对时间和空间的消耗很大，可以说是最暴力的方案。
多边形网格
后缀为.obj的文件存储的就是多边形网格信息，一般包含：
v ：顶点坐标
vt：纹理坐标
vn：法线方向
f：表示一个多边形面，由v vt vn组成
贝塞尔曲线
经典中的经典。
贝塞尔曲线用于设计光滑的曲线和曲面。
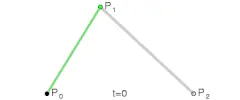
假设有两点b10和b11，在0时刻分别从b0和b1出发，向终点b1和b2沿线匀速移动，最后同时到达终点。
连接b10和b11，又有一点b20从b10出发，沿线向b11移动，并且和b10、b11同时到达各自的终点。
此时，b20移动过的路径即为贝塞尔曲线。
可以看下图，非常直观。
可以用de Casteljau算法来实现任意阶的贝塞尔曲线，基本思想是递归降阶，直至一阶返回。
贝塞尔曲线有诸多优秀的性质，如下。
- 几何不变性：
指某些几何特性不随坐标变换而变化的特性。Bezier曲线的形状仅与控制多边形各顶点的相对位置有关，而与坐标系的选择无关。 - 变差缩减性：
若Bezier曲线的特征多边形是一个平面图形，则平面内任意直线与贝赛尔曲线交点的个数不多于该直线与特征多边形的交点个数。 - 凸包性：
Bezier曲线始终落在控制点Pi构成的凸包内。
而想让分段贝塞尔曲线在控制点连接处平滑过渡，则要让连接处的切线大小相同，方向共线。
只需调整控制点的相对位置，就能得到各种平滑的曲线，它很适合在计算机中作图。也正因如此，它在计算机发展迅猛的今天还能大放光彩。
几何处理
- 网格细分（上采样）
顾名思义，将当前的三角形网格细分为多个更小的三角形。 - 网格简化（下采样）
顾名思义，将当前的三角形网格合并为一个更大的三角形。 - 网格正则化
顾名思义，将当前大小不一的各个三角形变得大小一致。
参考资料
以上笔记（含图片）总结自GAMES101课程及其PPT讲义。
GAMES101教程视频传送门
从零开始学图形学：10分钟看懂贝塞尔曲线
