【GAMES101】学习记录3-Shading
前言
时间不多了，得快马加鞭。这里整理出GAMES101-Lecture-07到10的内容。如有错误，欢迎斧正。
记录
着色
着色是将材质（material）应用于对象的过程。
着色有很多模型（Model），先从最经典的布林-冯模型（Blinn-Phong）开始。
布林-冯反射模型（Blinn-Phong Reflectance Model）
模型中的光通常会出现三种情况：
- 高光（Specular highlights）
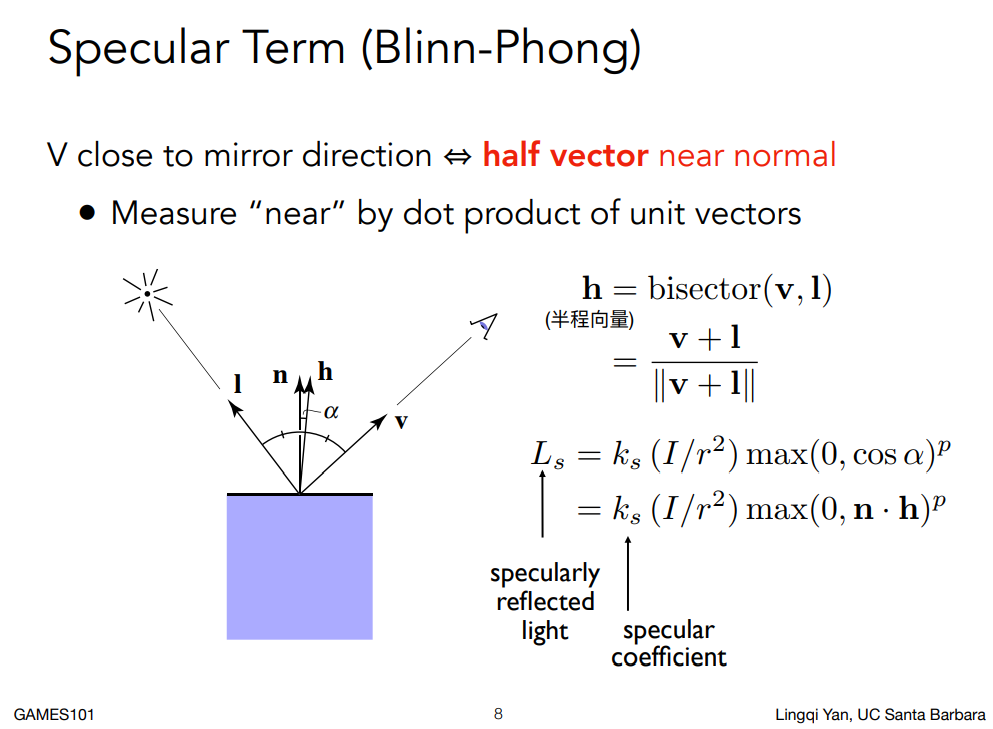
在上图中的参数中，l是光线方向，v是观测方向，n是法线方向。
值得注意的是，半程向量h在l和v的角平分线方向。利用它，我们可以求得视线能否在这一点看到高光，如下图。
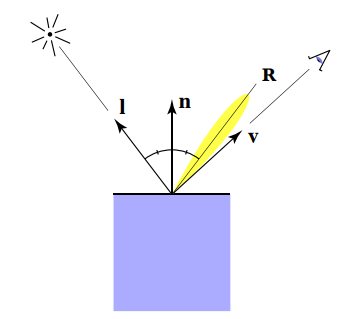
上图中，R是l的镜面反射方向。当R和v相靠足够近时（大概在图中的黄色区域），就能看到高光。
但R并不好求，而半程向量h很好求。
判断半程向量和法线方向是否相近，我们同样可以知道：某一点是否能看到高光。 - 漫反射光（Diffuse reflection）
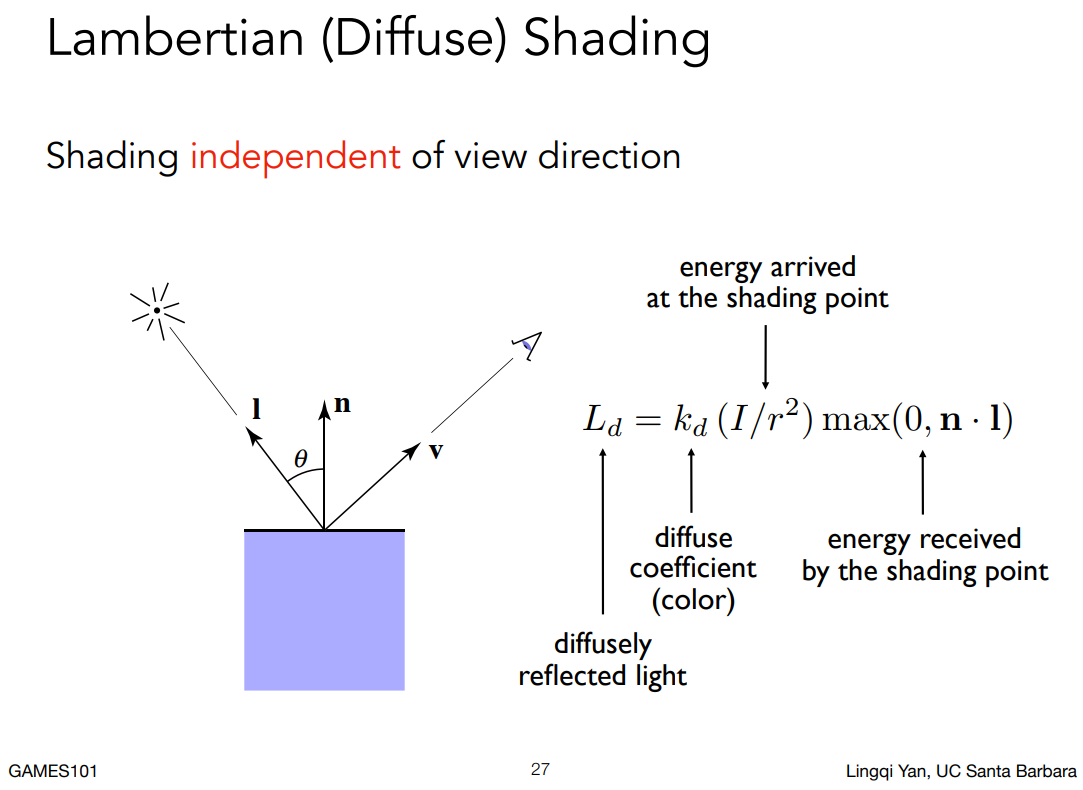
- 环境光（Ambient lighting）
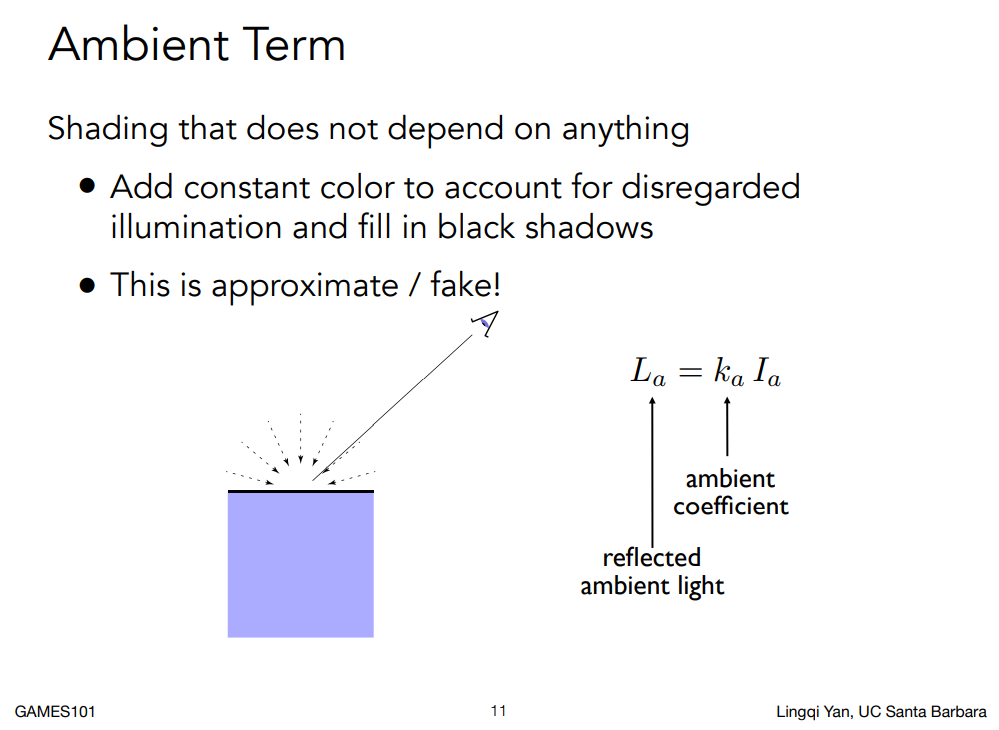
某一处的光照，即为上面三个参数之和。
着色频率
有三种着色频率：
- 逐面（flat）：依据平面的法线对整个面着色。
- 逐顶点（vertex）：根据平面法线，加权平均计算出各个顶点的法线，面中间点的颜色可根据插值得到。
- 逐像素（pixel）：在计算出顶点法线的基础上，插值得出每个像素点的法线方向，对每个像素着色。Phong模型就是如此。
一般来说，模型的精细程度：pixel > vertex > flat。不过也不绝对，因为当面或顶点足够小的时候，就可以说这三者的差别不大。
渲染管线基本流程
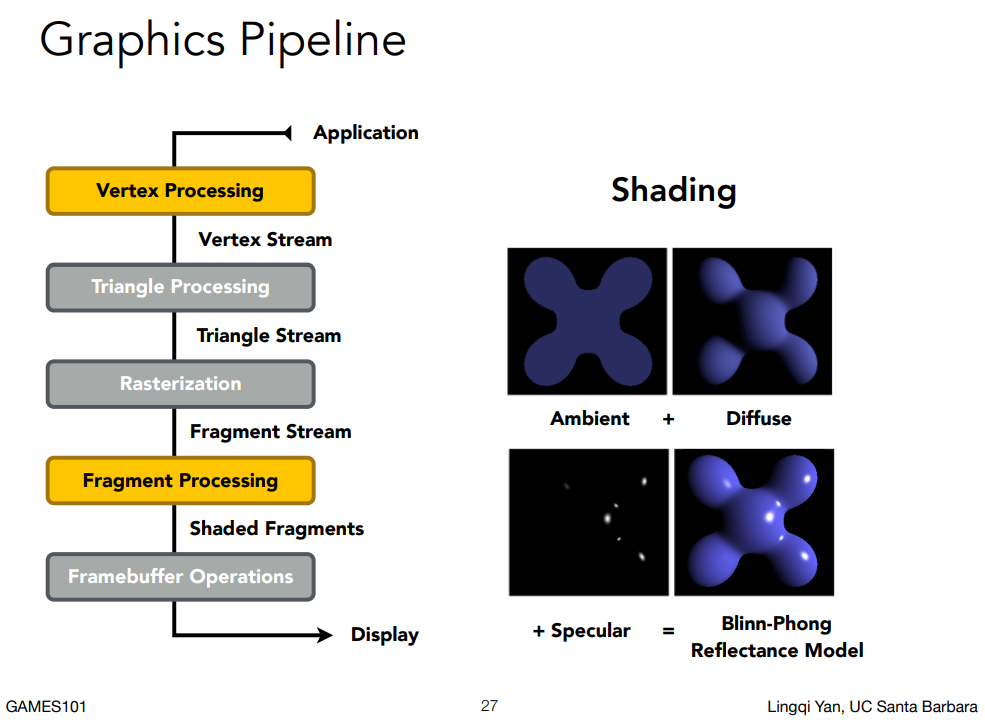
纹理映射
上面我们只讨论了光线明暗，现在我们来考虑纹理映射的问题。
重心坐标
先来复习一下利用重心坐标插值三角形内任意点。
有三角形ABC，则在三角形平面内任意一点都可以表示为三个顶点坐标的线性组合，如下图。
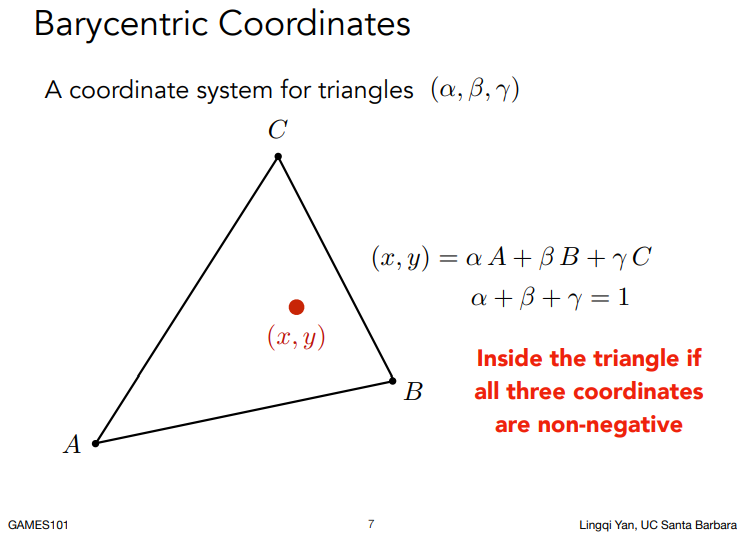
其中，（α，β，γ）即为点（x，y）对该三角形的重心坐标。
拿到了重心坐标，我们就可以利用它，对该点的颜色进行插值，得到一个平滑的颜色过渡。
纹理大小引发的问题
纹理过小
纹理过小，即纹理的分辨率不足。由于纹理本身的分辨率不足，我们渲染的图像也会出现分辨率低的问题。
但我们可以利用双线性插值应对这个问题，以减轻走样，如下图。
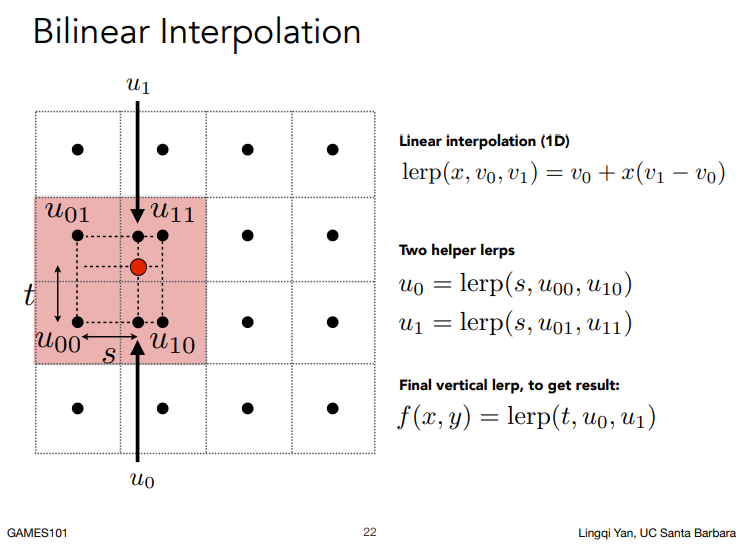
纹理过大
纹理过大，即纹理的分辨率过高。由于纹理分辨率过高，导致有时候会出现：一个屏幕像素包含了多个纹素。此时该像素不知道应该采样哪个纹素的值，如下。
有多种解决方案：
- 超采样（Supersampling），即取该像素所覆盖的纹素的值，求平均。但超采样的时间开销很大。
- 范围查询（Range Query），用空间换时间，引入Mipmap来节省时间。
Mipmap：根据一张贴图生成一系列贴图，每一张的分辨率都是上一张的一半，如下。
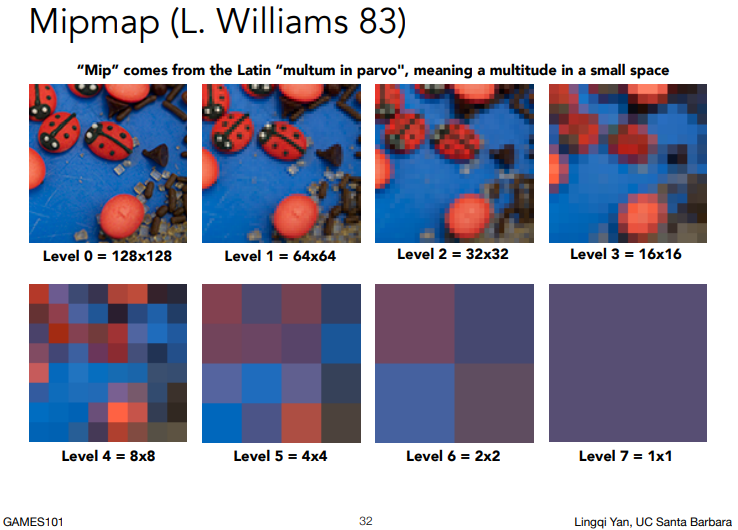
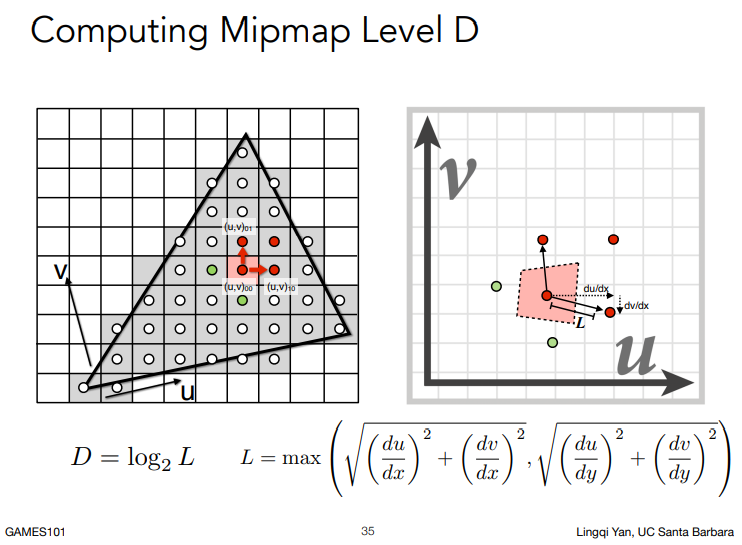
三线性插值（trilinear interpolation），是指在采样点所处Mipmap层级的两张相邻纹理中分别做双线性插值，最后将两个结果加权平均，如下。
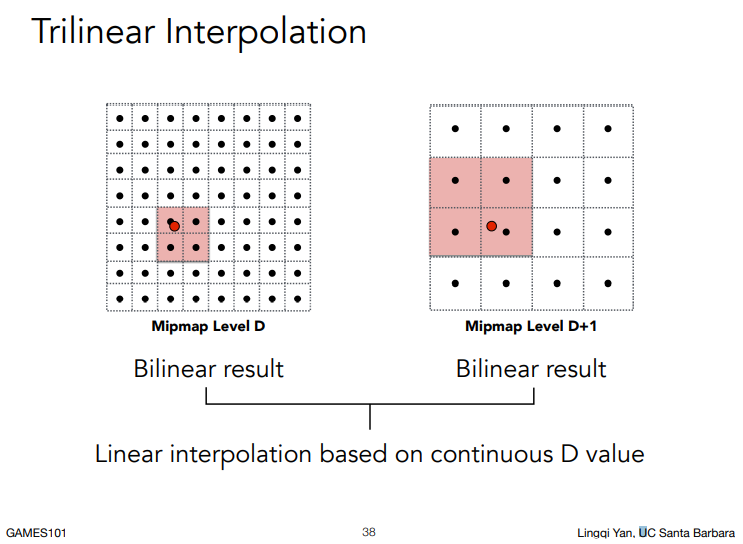
利用三线性插值，我们可以在层内和层与层之间得到一个非常平滑的变化，效果很好。
但Mipmap仍有缺陷，因为它的结果是近似结果而非准确结果，所以它会模糊掉远处的细节，如下。
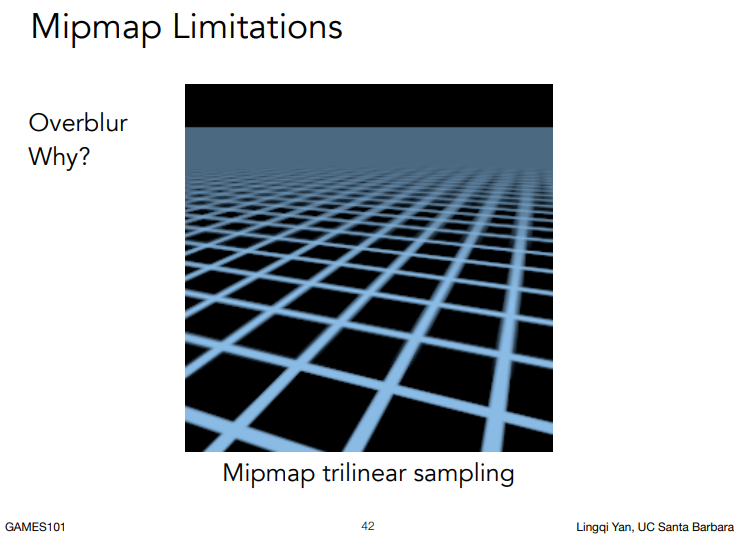
为了解决这个问题，可以引入Ripmap，使用各向异性过滤（Anisotropic Filtering）来解决。这里不过多展开。
纹理应用
- 环境贴图。
- 影响着色。
这里展开讲第二点：纹理可以表现物体上的凹凸状况。
凹凸贴图（Bump Mapping）
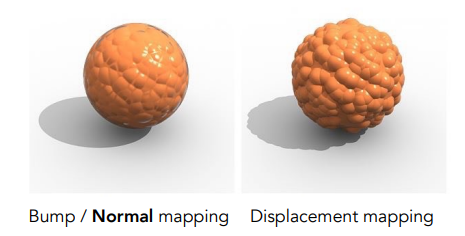
凹凸贴图可以在不添加更多三角形的情况下，增加曲面细节。复杂的纹理可以定义一个点的相对高度，在着色计算时引用进去，使得该点的光线明暗发生改变，以欺骗人的眼睛，让人以为这一点发生了凹凸。但是可以从某些细节发现它没有那么真实。
位移贴图（Displacement mapping）
位移贴图可以真正改变三角形顶点的位置。它弥补了凹凸贴图的缺点，看起来十分真实。
参考资料
以上笔记（含图片）总结自GAMES101课程及其PPT讲义。
GAMES101教程视频传送门
